DOCSLIB.ORG

Atomic Beam Measurements of Lifetimes of Metastable

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Atomic Beam Measurements of Lifetimes of Metastable ATOMIC BEAM MEASUREMENTS OF LIFETIMES OF METASTABLE EXCITED STATES. with particular reference to TEE INFLUENCE OF ELECTRIC FIELDS ON TEE LIFETIMES OF ATOMS IN METASTABLE STATES. A Thesis for the Degree of Doctor of Philosophy in the School of Physics, University of New South Wales. Submitted by: A.S. PEARL. October, 1967 ABSTRACT An atomic beam method was used to examine the influence of an electric field on the lifetime of the 2^S metastable state of o the helium atom. The (21S - 1^S) transition probability in the presence of an electric field was observed to depend on the electric field strength, F, according to 2 w (F) = w + aF o where wq is the natural decay rate of the 2^S state and a = 0.40 (KVcm ^sec ^ Evidence Is presented to show that the natural decay rate is given by w ^ 770 sec ^ o corresponding to a maximum lifetime of 1.3m sec. TABLE OF CONTENTS Page No. Chapter 1 INTRODUCTION 1 Chapter 2 HISTORICAL BACKGROUND 8 Introduction 8 2.1 Discovery and Classification of Forbidden Transitions 8 2.2 Forbidden Transitions Induced by Electric and Magnetic Fields 12 2.3 The i'etastability of the 2S < State in Hydrogen ~ 24 2.4 Electrostatic Quenching Measurements 30 2.5 Recent Work on Double Quantum Emission 31 1 2. G The Metastability of the 2 S and 3 2 S Helium Levels 34 Chapter 3 THEORY 36 Introduction 36 3.1 Spontaneous Forbidden Transitions in Radiation Theory 37 3.2 The Selection Rules 42 3.3 Higher Multipole Radiation 45 3.4 Multiple Quantum Transitions 47 1 3.5 The Natural Lifetime of the 2 S State of Helium 49 I d re No. 5.6 Forbidden Transitions in External Fields 51 3.7 Lifetime of He 2^S in an Electric Field 53 Chapter 4 METHODS AND BJJIBLSNT 61 Introduction 61 4.1 Method - General Description 61 4.2 Formation of Beam 62 4.3 Production of •¥etastable Sta tes 67 4.4 Detection of Atoms in Meta stable States 71 4.5 lhoton Detection 76 4.6 Calibration of lhoton Detection 78 4.7 The Electric Field 84 4.8 Experiment 1 and 2 - Analysis and Description 85 Chapter 5 E PERTH ENTAL RESULTS 94 5.1 Experiment 1 94 5.2 Sources of Spurious Photon Detector Signal 99 5.3 Estimate of the Lifetime of the 1 2 S Level by ihoton Counting 105 5.4 Deduction of the He 2^S Natural Lifetime from Data on Helium Afterglows 110 5.5 Experiment 2 - Electric Field Attenuation of ;:efcastable Flux 115 5.5 Summary and Comparison of Results 116 Chapter 6 ADDITIONAL EX] FJRIiv: ENTS 122 Introduction 122 6.1 Ratio of the He 2XS and 2 S Electron Impact Excitation Functions 122 6.2 Pressure Dependence of Photon Signal 127 6.3 Attenuation of Feta stable Beam by Helium Gas 133 6.4 Test for Double Quantum Decay 140 Chapter 7 CONCLUSION 142 7.1 Resume 142 7.2 Discussion 145 APPENDICES 150 A1 Solid Angle Determination 150 A2 Electron Impact Deflections 155 A3 He (n^F - l^S) Resonance Radiation 159 A4 Distribution of Velocity in the Atomic Beam 163 A5 Voltage Calibration 167 A CKNOVt LEDG'3’ ~EPiT 168 BIBLIOGPAPHY 169 1 CHAPTER 1. INTRODUCTION. The purpose of this research was to investigate the influence of an electric field on the radiative decay of the metastable 2^S Ievel of helium. Forbidden Transitions. When an atom emits or absorbs radiation It does so in discrete amounts determined by the restrictions on changes In Its Internal energy and angular momentum. The most general of the selection rules which apply to all atoms are:= (i) In an electric dipole (allowed) transition the total angular momentum of the atom either remains unchanged or changes by unity I.e. the permissable changes In the angular momentum fJT in units offiare described by relation AJ = 0, ± 1 with the additional restriction that transitions between zero angular momentum states J = 0 —J = 0 are strictly forbidden, I.e. forbidden for all first order (single photon) processes. (ii) In an electric dipole transition, there must be a change of parity between the initial and final states. For light atoms, In which there is negligible Interaction between the magnetic moments associated with the spin and orbital angular momentum, the above selection rule for J may be resolved info two independent rules, viz., AL 0 ± 1 L *■ 0 —L = 0 strictly forbidden where L Is the total orbital angular momentum of the atom, and AS = 0 where S is the total spin of the atom. For example, the He (2^S - 1^S) transition Is doubly forbidden, because the Initial and final states are spherically symmetric (J = 0) and because both states have the same parity. Since there are no alternative downward transitions available, (Fig. 1.1), the 2^S state Is metastable. There is a small probability of the occurrence of transitions which contravene these selection rules. Such transitions have been called forbidden transitions. Forbidden transitions can be spontaneous or enforced. Spontaneous forbidden transitions fall into two classes: (i) first order (higher multipole) transitions. (ii) second order transitions which Involve the simultaneous emission of two photons. In the absence of a field, the He 2^S state is expected to decay via the emission of two photons, because all single photon transitions are strictly forbidden. Perturbations external to or within the atom can lead to the occurrence of forbidden transitions. An external electric field modifies the charge distribution of an atom In a particular state and hence the applicability or "goodness" of Its orbital quantum number. In wave mechanical terms, an electric field "mixes" the wave function of the Ionization 24.59 eV I 3's __ 2-1° 3 3Pp 3D 33S 22.72 eV in 2 P 2 1.22 2 3P 2 I 20.96 2 S 20.61 E n erg y 2 3S 19.82 I s 1.1. Vi ' nw jiff ] ji r; vcfy 3 initial state with components of the wave function of energetically adjacent levels to which it is optically coupled. Thus it was anticipated that application of an electric field to helium atoms in the metastable 2^S state, would enhance the probability of the doubly forbidden (2^S - 1^S) transition. Interatomic and ionic electric fields in the cathode fall of discharges can cause the appearance of forbidden lines: lines arising from the electric field weakening of the azimuthal selection rule are known to spectroscopists as "enforced dipole lines". Some experiments on enforced dipole radiation were conducted in the 1930’s. The essential qualitative features were elucidated by a series of experiments in which the enforced lines were observed by the application of external electric fields to absorption cells. The Zeeman spectra of enforced radiation were studied by the simultaneous application of external electric and magnetic fields. The Hydrogen Metastable State, H2Si _ ______ _ ____________________ 2_* The choice of topic of this thesis was influenced by a series of post war experiments with atomic beams containing hydrogen atoms in the metastable 2S,state, (Lamb & Retherford (1951), Fite et a I 2 7 (1959)). The H2S± level is metastable because transitions to the ground 2 state are forbidden, both by the rule which strictly prohibits transitions between L = 0 states, and by the requirement of a change of parity. However, because of the near degeneracy of the 2S, and 2P± levels, the 2 2 wave function of the 2Si level is particularly susceptible to electric 4 field mixing with the 2P± wave function, weakening the metastability 2 of the 2S± level by causing it to undergo enforced dipole transitions 2 to the ground state. In these experiments which are described In the next Chapter of this thesis, the density of 2SL atoms was determined by 2 completely guenching them in electric fields/v 50Vcm \ Although Bethe (1933) and Lamb & Retherford (1951), had calculated the life­ time of the H2S± level in an electric field, no attempt was made to 2 measure it. Fite et al (1959) measured the natural lifetime of the H2S± level, and found that it decays by single quantum emission at 2 a rate about fifty times greater than the theoretically predicted (double photon) decay rate. Subsequent to the commencement of the present project, I.A. Sell in (1964) verified experimentally, the calculations of Lamb and Bethe (loc cit) pertaining to the lifetime of the H12S, 2 state In the presence of an electric field. Description of Present Project. Thus the present project, was concerned with two kinds of forbidden transition - (i) Two photon transitions, the expected mode of decay of the He 2^S level In the absence of a field. (il) Enforced dipole single photon transitions, with particular referenced the influence of an electric field on the decay rate of the He 2^S state. 5 In the case of the latter, since the relevant dipole matrix elements were known (Schiff & Peskeris, 1964) and calculation of the theoretical ’’quenching'’ is a relatively simple matter, it was possible to effect a direct comparison between experiment and theory. In the former case, the quest for an experimental estimate of the natural lifetime of the He 2^S level, was given added impetus by the publication (Dalgarno, 1966) of an accurate theoretical calculation in which the lifetime of the 2^S state was limited by double quantum -2 emission to a value of 2.2 x 10 sec. The basic plan of the experiment is illustrated schematically in Fig.
Load more

Recommended publications
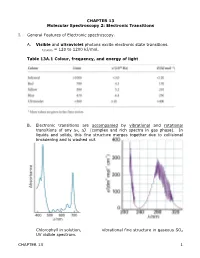
  • CHAPTER 13 Molecular Spectroscopy 2: Electronic Transitions
    CHAPTER 13 Molecular Spectroscopy 2: Electronic Transitions I. General Features of Electronic spectroscopy. A. Visible and ultraviolet photons excite electronic state transitions. εphoton = 120 to 1200 kJ/mol. Table 13A.1 Colour, frequency, and energy of light B. Electronic transitions are accompanied by vibrational and rotational transitions of any Δν, ΔJ (complex and rich spectra in gas phase). In liquids and solids, this fine structure merges together due to collisional broadening and is washed out. Chlorophyll in solution, vibrational fine structure in gaseous SO2 UV visible spectrum. CHAPTER 13 1 C. Molecules need not have permanent dipole to undergo electronic transitions. All that is required is a redistribution of electronic and nuclear charge between the initial and final electronic state. Transition intensity ~ |µ|2 where µ is the magnitude of the transition dipole moment given by: ˆ d µ = ∫ ψfinalµψ initial τ where µˆ = −e ∑ri + e ∑Ziri € electrons nuclei r vector position of the particle i = D. Franck-Condon principle: Because nuclei are so much more massive and € sluggish than electrons, electronic transitions can happen much faster than the nuclei can respond. Electronic transitions occur vertically on energy diagram at right. (Hence the name vertical transition) Transition probability depends on vibrational wave function overlap (Franck-Condon factor). In this example: ν = 0 ν’ = 0 have small overlap ν = 0 ν’ = 2 have greatest overlap Now because the total molecular wavefunction can be approximately factored into 2 terms, electronic wavefunction and the nuclear position wavefunction (using Born-Oppenheimer approx.) the transition dipole can also be factored into 2 terms also: S µ = µelectronic i,f S d Franck Condon factor i,j i,f = ∫ ψf,vibr ψi,vibr τ = − CHAPTER 13 2 See derivation “Justification 14.2” II.
    [Show full text]
  • Lecture B4 Vibrational Spectroscopy, Part 2 Quantum Mechanical SHO
    Lecture B4 Vibrational Spectroscopy, Part 2 Quantum Mechanical SHO. WHEN we solve the Schrödinger equation, we always obtain two things: 1. a set of eigenstates, |ψn>. 2. a set of eigenstate energies, En QM predicts the existence of discrete, evenly spaced, vibrational energy levels for the SHO. n = 0,1,2,3... For the ground state (n=0), E = ½hν. Notes: This is called the zero point energy. Optical selection rule -- SHO can absorb or emit light with a ∆n = ±1 The IR absorption spectrum for a diatomic molecule, such as HCl: diatomic Optical selection rule 1 -- SHO can absorb or emit light with a ∆n = ±1 Optical selection rule 2 -- a change in molecular dipole moment (∆μ/∆x) must occur with the vibrational motion. (Note: μ here means dipole moment). If a more realistic Morse potential is used in the Schrödinger Equation, these energy levels get scrunched together... ΔE=hν ΔE<hν The vibrational spectroscopy of polyatomic molecules gets more interesting... For diatomic or linear molecules: 3N-5 modes For nonlinear molecules: 3N-6 modes N = number of atoms in molecule The vibrational spectroscopy of polyatomic molecules gets more interesting... Optical selection rule 1 -- SHO can absorb or emit light with a ∆n = ±1 Optical selection rule 2 -- a change in molecular dipole moment (∆μ/∆x) must occur with the vibrational motion of a mode. Consider H2O (a nonlinear molecule): 3N-6 = 3(3)-6 = 3 Optical selection rule 2 -- a change in molecular dipole moment (∆μ/∆x) must occur with the vibrational motion of a mode. Consider H2O (a nonlinear molecule): 3N-6 = 3(3)-6 = 3 All bands are observed in the IR spectrum.
    [Show full text]
  • Lecture 17 Highlights
    Lecture 23 Highlights The phenomenon of Rabi oscillations is very different from our everyday experience of how macroscopic objects (i.e. those made up of many atoms) absorb electromagnetic radiation. When illuminated with light (like French fries at McDonalds) objects tend to steadily absorb the light and heat up to a steady state temperature, showing no signs of oscillation with time. We did a calculation of the transition probability of an atom illuminated with a broad spectrum of light and found that the probability increased linearly with time, leading to a constant transition rate. This difference comes about because the many absorption processes at different frequencies produce a ‘smeared-out’ response that destroys the coherent Rabi oscillations and results in a classical incoherent absorption. Selection Rules All of the transition probabilities are proportional to “dipole matrix elements,” such as x jn above. These are similar to dipole moment calculations for a charge distribution in classical physics, except that they involve the charge distribution in two different states, connected by the dipole operator for the transition. In many cases these integrals are zero because of symmetries of the associated wavefunctions. This gives rise to selection rules for possible transitions under the dipole approximation (atom size much smaller than the electromagnetic wave wavelength). For example, consider the matrix element z between states of the n,l , m ; n ', l ', m ' Hydrogen atom labeled by the quantum numbers n,,l m and n',','l m : z = ψ()()r z ψ r d3 r n,l , m ; n ', l ', m ' ∫∫∫ n,,l m n',l ', m ' To make progress, first consider just the φ integral.
    [Show full text]
  • Introduction to Differential Equations
    Quantum Dynamics – Quick View Concepts of primary interest: The Time-Dependent Schrödinger Equation Probability Density and Mixed States Selection Rules Transition Rates: The Golden Rule Sample Problem Discussions: Tools of the Trade Appendix: Classical E-M Radiation POSSIBLE ADDITIONS: After qualitative section, do the two state system, and then first and second order transitions (follow Fitzpatrick). Chain together the dipole rules to get l = 2,0,-2 and m = -2, -2, … , 2. ??Where do we get magnetic rules? Look at the canonical momentum and the Asquared term. Schrödinger, Erwin (1887-1961) Austrian physicist who invented wave mechanics in 1926. Wave mechanics was a formulation of quantum mechanics independent of Heisenberg's matrix mechanics. Like matrix mechanics, wave mechanics mathematically described the behavior of electrons and atoms. The central equation of wave mechanics is now known as the Schrödinger equation. Solutions to the equation provide probability densities and energy levels of systems. The time-dependent form of the equation describes the dynamics of quantum systems. http://scienceworld.wolfram.com/biography/Schroedinger.html © 1996-2006 Eric W. Weisstein www-history.mcs.st-andrews.ac.uk/Biographies/Schrodinger.html Quantum Dynamics: A Qualitative Introduction Introductory quantum mechanics focuses on time-independent problems leaving Contact: [email protected] dynamics to be discussed in the second term. Energy eigenstates are characterized by probability density distributions that are time-independent (static). There are examples of time-dependent behavior that are by demonstrated by rather simple introductory problems. In the case of a particle in an infinite well with the range [ 0 < x < a], the mixed state below exhibits time-dependence.
    [Show full text]
  • HJ Lipkin the Weizmann Institute of Science Rehovot, Israel
    WHO UNDERSTANDS THE ZWEIG-IIZUKA RULE? H.J. Lipkin The Weizmann Institute of Science Rehovot, Israel Abstract: The theoretical basis of the Zweig-Iizuka Ru le is discussed with the emphasis on puzzles and paradoxes which remain open problems . Detailed analysis of ZI-violating transitions arising from successive ZI-allowed transitions shows that ideal mixing and additional degeneracies in the particle spectrum are required to enable cancellation of these higher order violations. A quantitative estimate of the observed ZI-violating f' + 2rr decay be second order transitions via the intermediate KK state agrees with experiment when only on-shell contributions are included . This suggests that ZI-violations for old particles are determined completely by on-shell contributions and cannot be used as input to estimate ZI-violation for new particle decays where no on-shell intermediate states exist . 327 INTRODUCTION - SOME BASIC QUESTIONS 1 The Zweig-Iizuka rule has entered the folklore of particle physics without any clear theoretical understanding or justification. At the present time nobody really understands it, and anyone who claims to should not be believed. Investigating the ZI rule for the old particles raises many interesting questions which may lead to a better understanding of strong interactions as well as giving additional insight into the experimentally observed suppression of new particle decays attributed to the ZI rule. This talk follows an iconoclastic approach emphasizing embarrassing questions with no simple answers which might lead to fruitful lines of investigation. Both theoretical and experimental questions were presented in the talk. However, the experimental side is covered in a recent paper2 and is not duplicated here.
    [Show full text]
  • UV-Vis. Molecular Absorption Spectroscopy
    UV-Vis. Molecular Absorption Spectroscopy Prof. Tarek A. Fayed UV-Vis. Electronic Spectroscopy The interaction of molecules with ultraviolet and visible light may results in absorption of photons. This results in electronic transition, involving valance electrons, from ground state to higher electronic states (called excited states). The promoted electrons are electrons of the highest molecular orbitals HOMO. Absorption of ultraviolet and visible radiation in organic molecules is restricted to certain functional groups (known as chromophores) that contain valence electrons of low excitation energy. A chromophore is a chemical entity embedded within a molecule that absorbs radiation at the same wavelength in different molecules. Examples of Chromophores are dienes, aromatics, polyenes and conjugated ketones, etc. Types of electronic transitions Electronic transitions that can take place are of three types which can be considered as; Transitions involving p-, s-, and n-electrons. Transitions involving charge-transfer electrons. Transitions involving d- and f-electrons in metal complexes. Most absorption spectroscopy of organic molecules is based on transitions of n- or -electrons to the *-excited state. These transitions fall in an experimentally convenient region of the spectrum (200 - 700 nm), and need an unsaturated group in the molecule to provide the -electrons. In vacuum UV or far UV (λ<190 nm ) In UV/VIS For formaldehyde molecule; Selection Rules of electronic transitions Electronic transitions may be allowed or forbidden transitions, as reflected by appearance of an intense or weak band according to the magnitude of εmax, and is governed by the following selection rules : 1. Spin selection rule (△S = 0 for the transition to be allowed): there should be no change in spin orientation i.
    [Show full text]
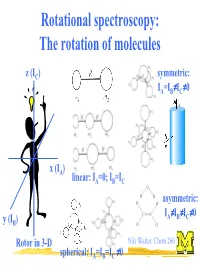
  • Rotational Spectroscopy: the Rotation of Molecules
    Rotational spectroscopy: The rotation of molecules z (IC) symmetric: ≠ ≠ IA=IB IC 0 x (IA) linear: IA=0; IB=IC asymmetric: ≠ ≠ ≠ IA IB IC 0 y (IB) Rotor in 3-D Nils Walter: Chem 260 ≠ spherical: IA=IB=IC 0 The moment of inertia for a diatomic (linear) rigid rotor r definition: r = r1 + r2 m1 m2 C(enter of mass) r1 r2 Moment of inertia: Balancing equation: m1r1 = m2r2 2 2 I = m1r1 + m2r2 m m ⇒ I = 1 2 r 2 = µr 2 µ = reduced mass + m1 m2 Nils Walter: Chem 260 Solution of the Schrödinger equation for the rigid diatomic rotor h2 (No potential, − V 2Ψ = EΨ µ only kinetic 2 energy) ⇒ EJ = hBJ(J+1); rot. quantum number J = 0,1,2,... h B = [Hz] 4πI ⇒ EJ+1 -EJ = 2hB(J+1) Nils Walter: Chem 260 Selection rules for the diatomic rotor: 1. Gross selection rule Light is a transversal electromagnetic wave a polar rotor appears to have an oscillating ⇒ a molecule must be polar to electric dipole Nils Walter: Chem 260 be able to interact with light Selection rules for the diatomic rotor: 2. Specific selection rule rotational quantum number J = 0,1,2,… describes the angular momentum of a molecule (just like electronic orbital quantum number l=0,1,2,...) and light behaves as a particle: photons have a spin of 1, i.e., an angular momentum of one unit and the total angular momentum upon absorption or emission of a photon has to be preserved ⇒⇒∆∆J = ± 1 Nils Walter: Chem 260 Okay, I know you are dying for it: Schrödinger also can explain the ∆J = ± 1 selection rule Transition dipole µ = Ψ µΨ dτ moment fi ∫ f i initial state final state ⇒ only if this integral
    [Show full text]
  • Shaping Polaritons to Reshape Selection Rules
    Shaping Polaritons to Reshape Selection Rules 1,2 2 3 2 2,4 Francisco Machado∗ , Nicholas Rivera∗ , Hrvoje Buljan , Marin Soljaˇci´c , Ido Kaminer 1Department of Physics, University of California, Berkeley, CA 97420, USA 2Department of Physics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA 3Department of Physics, University of Zagreb, Zagreb 10000, Croatia. 4Department of Electrical Engineering, Technion, Israel Institute of Technology, Haifa 32000, Israel. The discovery of orbital angular momentum (OAM) in light established a new degree of freedom by which to control not only its flow but also its interaction with matter. Here, we show that by shaping extremely sub-wavelength polariton modes, for example by imbuing plasmon and phonon polariton with OAM, we engineer which transitions are allowed or forbidden in electronic systems such as atoms, molecules, and artificial atoms. Crucial to the feasibility of these engineered selection rules is the access to conventionally forbidden transitions afforded by sub-wavelength polaritons. We also find that the position of the absorbing atom provides a surprisingly rich parameter for controlling which absorption processes dominate over others. Additional tunability can be achieved by altering the polaritonic properties of the substrate, for example by tuning the carrier density in graphene, potentially enabling electronic control over selection rules. Our findings are best suited to OAM-carrying polaritonic modes that can be created in graphene, monolayer conductors, thin metallic films, and thin films of polar dielectrics such as boron nitride. By building on these findings we foresee the complete engineering of spectroscopic selection rules through the many degrees of freedom in the shape of optical fields.
    [Show full text]
  • Laporte Selection Rule (Only for Systems with Inversion Symmetry)
    UV/Vis-Spectroscopy = investigation of electronic transitions within a molecule Energy Electronic transition Emission Excited state Ea hn Ground state E Absorption g c Conversion factors ~ –1 –1 E Ea Eg hn h hcn 1 eV = 8066 cm = 96.5 kJ•mol 1 eV = 1.602•10–19 J n+ UV/Vis spectra of the [M(H2O)6] cations general observation: d1, d4, d6, d9 (one band) d2, d3, d7, d8 (three bands) d5 (several sharp, relatively weak bands) (only high-spin compounds) d0, d10: no absorption bands Intensities of absorption bands –1 –1 emax (extinction coefficient), dimension M cm SiO2 cuvette Lambert-Beer law: emax = E / (c·l) 5 –1 –1 range: emax = 0 to > 10 M cm l = diameter e of cuvette emax 1 n n~ c 400 nm = 25000 cm-1 200 nm = 50000 cm-1 max Selection rules* spin multiplicity MS = 2S+1 S = Ss = n/2 (total spin quantum 1. Spin selection rule S = 0 or MS = 0 number) (Transition between same spin states allowed: singlet -> singlet, triplet -> triplet, others are forbidden: singlet -> triplet, doublet -> singlet, etc.) 2+ [Mn(H2O)6] Pauli-Principle not obeyed hn S = 5/2 S = 5/2 S = 3/2 S = 1, forbidden e < 1 M‒1cm‒1 .. only one electron is involved in any transition max * were developed for metal atoms and ions (where they are rigorously obeyed), not complexes Spin selection rule 2+ [Co(H2O)6] 3+ Pauli Prinziple [Cr(NH3)6] obeyed hn S = 3/2 S = 3/2 S = 0, allowed ‒1 ‒1 emax = 1-10 M cm In the case of spin orbit coupling (as is the case for trans.-metal complexes), the spin-selection rule is partially lifted (=> weak, so-called inter-combination bands arise with e = 0.01 – 1.0 M‒1cm‒1) 4 2 III III II (example: A2g→ Eg- transition, in the case of Cr , l.s.-Co , or Mn ) an e ~ 0.01 M‒1cm‒1 is hardly detectable Orbital selection rule L = 1 2.
    [Show full text]
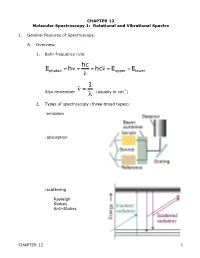
  • CHAPTER 12 Molecular Spectroscopy 1: Rotational and Vibrational Spectra
    CHAPTER 12 Molecular Spectroscopy 1: Rotational and Vibrational Spectra I. General Features of Spectroscopy. A. Overview. 1. Bohr frequency rule: hc Ephoton = hν = = hcν˜ = Eupper −Elower λ 1 Also remember ν˜ = (usually in cm-1) λ € 2. Types of spectroscopy (three broad types): -emission € -absorption -scattering Rayleigh Stokes Anti-Stokes CHAPTER 12 1 3. The electromagnetic spectrum: Region λ Processes gamma <10 pm nuclear state changes x-ray 10 pm – 10 nm inner shell e- transition UV 10 nm – 400 nm electronic trans in valence shell VIS 400 – 750 nm electronic trans in valence shell IR 750 nm – 1 mm Vibrational state changes microwave 1 mm – 10 cm Rotational state changes radio 10 cm – 10 km NMR - spin state changes 4. Classical picture of light absorption – since light is oscillating electric and magnetic field, interaction with matter depends on interaction with fluctuating dipole moments, either permanent or temporary. Discuss vibrational, rotational, electronic 5. Quantum picture: Einstein identified three contributions to transitions between states: a. stimulated absorption b. stimulated emission c. spontaneous emission Stimulated absorption transition probability w is proportional to the energy density ρ of radiation through a proportionality constant B w=B ρ The total rate of absorption W depends on how many molecules N in the light path, so: W = w N = N B ρ CHAPTER 12 2 Now what is B? Consider plane-polarized light (along z-axis), can cause transition if the Q.M. transition dipole moment is non-zero. µ = ψ *µˆ ψdτ ij ∫ j z i Where µˆ z = z-component of electric dipole operator of atom or molecule Example: H-atom € € - e r + µˆ z = −er Coefficient of absorption B (intrinsic ability to absorb light) 2 µij B = 6ε 2€ Einstein B-coefficient of stimulated absorption o if 0, transition i j is allowed µ ij ≠ → µ = 0 forbidden € ij € 6.
    [Show full text]
  • Wls-76/42-Ph
    WlS-76/42-Ph A KlfO UNDERSTANDS THE IhCIG-IIZUKA RULE? H.J. Lipkin The Kctzsann Institute of Science Rchovot, Israel Abstract: The theoretical basis of the Zweig-Iizuka Rule is discussed *ith the emphasis on puzzles and . paradoxes which remain open problems. Detailed analysis of Zl-violating transitions arising from successive Zl-allowcd transitions shows that ideal mixing and additional degeneracies in the particle spectrum are required to enable cancellation of these higher order violations. A quantitative estimate of the observed Zl-violating f •* 2ff decay be second order transitions via the intermediate KK state agrees with experiment when only on-shell contributions are included. This suggests that Zl-violations for old particles are determined completely by on-shell contributions and cannot be used as input to estimate Zl-violation for new particle decays where no on-shell intermediate states exist. t INTRODUCTION - SOMli BASIC QULSHONS The Zwcig-Iituka rule has entered the folklore of particle physics without any clear theoretical understanding or justification. At the present time nobody really understands it, and anyone who clliis to should not be believed. Investigating the ZI rule for the old particles raises many interesting questions which say lead to a better understanding of strong interactions as well as giving additional insight into the experiocntally observed suppression of new particle decays attributed to the ZI rule. This talk follows an iconoclastic approach emphasizing embarrassing questions with no simple answers which Bight lead to fruitful lines of investigation. Both theoretical and experimental questions were presented in the talk. However, 2 the experimental side is covered in a recent paper and is not duplicated here.
    [Show full text]
  • Diatomic Vibrational Spectra
    Diatomic vibrational spectra Molecular vibrations Typical potential energy curve of a diatomic molecule: Parabolic approximation close to Re: 1 V kx2 x R R 2 e k = force constant of the bond. The steeper the walls of the potential, the stiffer the bond, the greater the force constant. Connection between the shape of molecular potential energy curve and k: we expand V(x) around R = Re by a Taylor series: 2 2 dV 1 d V 2 1 d V 2 Vx V0 x x ... x dx 2 2 2 2 0 dx 0 dx 0 V(0) = constant set arbitrarily to zero. first derivative of V is 0 at the minimum. for small displacements we ignore all high terms. Hence, the first approximation to a molecular potential energy curve is a parabolic potential with: d2V k 2 dx 0 if V(x) is sharply curved, k is large. if V(x) is wide and shallow, k is small. Schrödinger equation for the relative motion of two atoms of masses m1 and m2 with a parabolic potential energy: 2 d2 1 kx2 E 2 2meff dx 2 m1m2 where meff = effective (or reduced) mass: meff m1 m2 Use of meff to consider the problem from the perspective of the motion of molecule as a whole. Example: homonuclear diatomic m1 = m2 = m: meff m / 2. XH, where mX >> mH: meff mH. Same Schrödinger equation as for the particle of mass m undergoing harmonic motion. Therefore, the permitted vibrational energy levels are: 1 k En n with: and: n = 0, 1, 2, … 2 meff The vibrational wavefunctions are the same as those discussed for the harmonic oscillator.
    [Show full text]