Chapter 17 Weak Interactions
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

The Role of Strangeness in Ultrarelativistic Nuclear
HUTFT THE ROLE OF STRANGENESS IN a ULTRARELATIVISTIC NUCLEAR COLLISIONS Josef Sollfrank Research Institute for Theoretical Physics PO Box FIN University of Helsinki Finland and Ulrich Heinz Institut f ur Theoretische Physik Universitat Regensburg D Regensburg Germany ABSTRACT We review the progress in understanding the strange particle yields in nuclear colli sions and their role in signalling quarkgluon plasma formation We rep ort on new insights into the formation mechanisms of strange particles during ultrarelativistic heavyion collisions and discuss interesting new details of the strangeness phase di agram In the main part of the review we show how the measured multistrange particle abundances can b e used as a testing ground for chemical equilibration in nuclear collisions and how the results of such an analysis lead to imp ortant con straints on the collision dynamics and spacetime evolution of high energy heavyion reactions a To b e published in QuarkGluon Plasma RC Hwa Eds World Scientic Contents Introduction Strangeness Pro duction Mechanisms QuarkGluon Pro duction Mechanisms Hadronic Pro duction Mechanisms Thermal Mo dels Thermal Parameters Relative and Absolute Chemical Equilibrium The Partition Function The Phase Diagram of Strange Matter The Strange Matter Iglo o Isentropic Expansion Trajectories The T ! Limit of the Phase Diagram -

Higgs Bosons and Supersymmetry
Higgs bosons and Supersymmetry 1. The Higgs mechanism in the Standard Model | The story so far | The SM Higgs boson at the LHC | Problems with the SM Higgs boson 2. Supersymmetry | Surpassing Poincar´e | Supersymmetry motivations | The MSSM 3. Conclusions & Summary D.J. Miller, Edinburgh, July 2, 2004 page 1 of 25 1. Electroweak Symmetry Breaking in the Standard Model 1. Electroweak Symmetry Breaking in the Standard Model Observation: Weak nuclear force mediated by W and Z bosons • M = 80:423 0:039GeV M = 91:1876 0:0021GeV W Z W couples only to left{handed fermions • Fermions have non-zero masses • Theory: We would like to describe electroweak physics by an SU(2) U(1) gauge theory. L ⊗ Y Left{handed fermions are SU(2) doublets Chiral theory ) right{handed fermions are SU(2) singlets f There are two problems with this, both concerning mass: gauge symmetry massless gauge bosons • SU(2) forbids m)( ¯ + ¯ ) terms massless fermions • L L R R L ) D.J. Miller, Edinburgh, July 2, 2004 page 2 of 25 1. Electroweak Symmetry Breaking in the Standard Model Higgs Mechanism Introduce new SU(2) doublet scalar field (φ) with potential V (φ) = λ φ 4 µ2 φ 2 j j − j j Minimum of the potential is not at zero 1 0 µ2 φ = with v = h i p2 v r λ Electroweak symmetry is broken Interactions with scalar field provide: Gauge boson masses • 1 1 2 2 MW = gv MZ = g + g0 v 2 2q Fermion masses • Y ¯ φ m = Y v=p2 f R L −! f f 4 degrees of freedom., 3 become longitudinal components of W and Z, one left over the Higgs boson D.J. -

Quantum Field Theory*
Quantum Field Theory y Frank Wilczek Institute for Advanced Study, School of Natural Science, Olden Lane, Princeton, NJ 08540 I discuss the general principles underlying quantum eld theory, and attempt to identify its most profound consequences. The deep est of these consequences result from the in nite number of degrees of freedom invoked to implement lo cality.Imention a few of its most striking successes, b oth achieved and prosp ective. Possible limitation s of quantum eld theory are viewed in the light of its history. I. SURVEY Quantum eld theory is the framework in which the regnant theories of the electroweak and strong interactions, which together form the Standard Mo del, are formulated. Quantum electro dynamics (QED), b esides providing a com- plete foundation for atomic physics and chemistry, has supp orted calculations of physical quantities with unparalleled precision. The exp erimentally measured value of the magnetic dip ole moment of the muon, 11 (g 2) = 233 184 600 (1680) 10 ; (1) exp: for example, should b e compared with the theoretical prediction 11 (g 2) = 233 183 478 (308) 10 : (2) theor: In quantum chromo dynamics (QCD) we cannot, for the forseeable future, aspire to to comparable accuracy.Yet QCD provides di erent, and at least equally impressive, evidence for the validity of the basic principles of quantum eld theory. Indeed, b ecause in QCD the interactions are stronger, QCD manifests a wider variety of phenomena characteristic of quantum eld theory. These include esp ecially running of the e ective coupling with distance or energy scale and the phenomenon of con nement. -
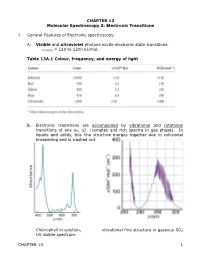
CHAPTER 13 Molecular Spectroscopy 2: Electronic Transitions
CHAPTER 13 Molecular Spectroscopy 2: Electronic Transitions I. General Features of Electronic spectroscopy. A. Visible and ultraviolet photons excite electronic state transitions. εphoton = 120 to 1200 kJ/mol. Table 13A.1 Colour, frequency, and energy of light B. Electronic transitions are accompanied by vibrational and rotational transitions of any Δν, ΔJ (complex and rich spectra in gas phase). In liquids and solids, this fine structure merges together due to collisional broadening and is washed out. Chlorophyll in solution, vibrational fine structure in gaseous SO2 UV visible spectrum. CHAPTER 13 1 C. Molecules need not have permanent dipole to undergo electronic transitions. All that is required is a redistribution of electronic and nuclear charge between the initial and final electronic state. Transition intensity ~ |µ|2 where µ is the magnitude of the transition dipole moment given by: ˆ d µ = ∫ ψfinalµψ initial τ where µˆ = −e ∑ri + e ∑Ziri € electrons nuclei r vector position of the particle i = D. Franck-Condon principle: Because nuclei are so much more massive and € sluggish than electrons, electronic transitions can happen much faster than the nuclei can respond. Electronic transitions occur vertically on energy diagram at right. (Hence the name vertical transition) Transition probability depends on vibrational wave function overlap (Franck-Condon factor). In this example: ν = 0 ν’ = 0 have small overlap ν = 0 ν’ = 2 have greatest overlap Now because the total molecular wavefunction can be approximately factored into 2 terms, electronic wavefunction and the nuclear position wavefunction (using Born-Oppenheimer approx.) the transition dipole can also be factored into 2 terms also: S µ = µelectronic i,f S d Franck Condon factor i,j i,f = ∫ ψf,vibr ψi,vibr τ = − CHAPTER 13 2 See derivation “Justification 14.2” II. -

Particle Physics Dr Victoria Martin, Spring Semester 2012 Lecture 12: Hadron Decays
Particle Physics Dr Victoria Martin, Spring Semester 2012 Lecture 12: Hadron Decays !Resonances !Heavy Meson and Baryons !Decays and Quantum numbers !CKM matrix 1 Announcements •No lecture on Friday. •Remaining lectures: •Tuesday 13 March •Friday 16 March •Tuesday 20 March •Friday 23 March •Tuesday 27 March •Friday 30 March •Tuesday 3 April •Remaining Tutorials: •Monday 26 March •Monday 2 April 2 From Friday: Mesons and Baryons Summary • Quarks are confined to colourless bound states, collectively known as hadrons: " mesons: quark and anti-quark. Bosons (s=0, 1) with a symmetric colour wavefunction. " baryons: three quarks. Fermions (s=1/2, 3/2) with antisymmetric colour wavefunction. " anti-baryons: three anti-quarks. • Lightest mesons & baryons described by isospin (I, I3), strangeness (S) and hypercharge Y " isospin I=! for u and d quarks; (isospin combined as for spin) " I3=+! (isospin up) for up quarks; I3="! (isospin down) for down quarks " S=+1 for strange quarks (additive quantum number) " hypercharge Y = S + B • Hadrons display SU(3) flavour symmetry between u d and s quarks. Used to predict the allowed meson and baryon states. • As baryons are fermions, the overall wavefunction must be anti-symmetric. The wavefunction is product of colour, flavour, spin and spatial parts: ! = "c "f "S "L an odd number of these must be anti-symmetric. • consequences: no uuu, ddd or sss baryons with total spin J=# (S=#, L=0) • Residual strong force interactions between colourless hadrons propagated by mesons. 3 Resonances • Hadrons which decay due to the strong force have very short lifetime # ~ 10"24 s • Evidence for the existence of these states are resonances in the experimental data Γ2/4 σ = σ • Shape is Breit-Wigner distribution: max (E M)2 + Γ2/4 14 41. -

Lecture B4 Vibrational Spectroscopy, Part 2 Quantum Mechanical SHO
Lecture B4 Vibrational Spectroscopy, Part 2 Quantum Mechanical SHO. WHEN we solve the Schrödinger equation, we always obtain two things: 1. a set of eigenstates, |ψn>. 2. a set of eigenstate energies, En QM predicts the existence of discrete, evenly spaced, vibrational energy levels for the SHO. n = 0,1,2,3... For the ground state (n=0), E = ½hν. Notes: This is called the zero point energy. Optical selection rule -- SHO can absorb or emit light with a ∆n = ±1 The IR absorption spectrum for a diatomic molecule, such as HCl: diatomic Optical selection rule 1 -- SHO can absorb or emit light with a ∆n = ±1 Optical selection rule 2 -- a change in molecular dipole moment (∆μ/∆x) must occur with the vibrational motion. (Note: μ here means dipole moment). If a more realistic Morse potential is used in the Schrödinger Equation, these energy levels get scrunched together... ΔE=hν ΔE<hν The vibrational spectroscopy of polyatomic molecules gets more interesting... For diatomic or linear molecules: 3N-5 modes For nonlinear molecules: 3N-6 modes N = number of atoms in molecule The vibrational spectroscopy of polyatomic molecules gets more interesting... Optical selection rule 1 -- SHO can absorb or emit light with a ∆n = ±1 Optical selection rule 2 -- a change in molecular dipole moment (∆μ/∆x) must occur with the vibrational motion of a mode. Consider H2O (a nonlinear molecule): 3N-6 = 3(3)-6 = 3 Optical selection rule 2 -- a change in molecular dipole moment (∆μ/∆x) must occur with the vibrational motion of a mode. Consider H2O (a nonlinear molecule): 3N-6 = 3(3)-6 = 3 All bands are observed in the IR spectrum. -

Weak Interaction Processes: Which Quantum Information Is Revealed?
Weak Interaction Processes: Which Quantum Information is revealed? B. C. Hiesmayr1 1University of Vienna, Faculty of Physics, Boltzmanngasse 5, 1090 Vienna, Austria We analyze the achievable limits of the quantum information processing of the weak interaction revealed by hyperons with spin. We find that the weak decay process corresponds to an interferometric device with a fixed visibility and fixed phase difference for each hyperon. Nature chooses rather low visibilities expressing a preference to parity conserving or violating processes (except for the decay Σ+ pπ0). The decay process can be considered as an open quantum channel that carries the information of the−→ hyperon spin to the angular distribution of the momentum of the daughter particles. We find a simple geometrical information theoretic 1 α interpretation of this process: two quantization axes are chosen spontaneously with probabilities ±2 where α is proportional to the visibility times the real part of the phase shift. Differently stated the weak interaction process corresponds to spin measurements with an imperfect Stern-Gerlach apparatus. Equipped with this information theoretic insight we show how entanglement can be measured in these systems and why Bell’s nonlocality (in contradiction to common misconception in literature) cannot be revealed in hyperon decays. We study also under which circumstances contextuality can be revealed. PACS numbers: 03.67.-a, 14.20.Jn, 03.65.Ud Weak interactions are one out of the four fundamental in- systems. teractions that we think that rules our universe. The weak in- Information theoretic content of an interfering and de- teraction is the only interaction that breaks the parity symme- caying system: Let us start by assuming that the initial state try and the combined charge-conjugation–parity( P) symme- of a decaying hyperon is in a separable state between momen- C try. -

1 Drawing Feynman Diagrams
1 Drawing Feynman Diagrams 1. A fermion (quark, lepton, neutrino) is drawn by a straight line with an arrow pointing to the left: f f 2. An antifermion is drawn by a straight line with an arrow pointing to the right: f f 3. A photon or W ±, Z0 boson is drawn by a wavy line: γ W ±;Z0 4. A gluon is drawn by a curled line: g 5. The emission of a photon from a lepton or a quark doesn’t change the fermion: γ l; q l; q But a photon cannot be emitted from a neutrino: γ ν ν 6. The emission of a W ± from a fermion changes the flavour of the fermion in the following way: − − − 2 Q = −1 e µ τ u c t Q = + 3 1 Q = 0 νe νµ ντ d s b Q = − 3 But for quarks, we have an additional mixing between families: u c t d s b This means that when emitting a W ±, an u quark for example will mostly change into a d quark, but it has a small chance to change into a s quark instead, and an even smaller chance to change into a b quark. Similarly, a c will mostly change into a s quark, but has small chances of changing into an u or b. Note that there is no horizontal mixing, i.e. an u never changes into a c quark! In practice, we will limit ourselves to the light quarks (u; d; s): 1 DRAWING FEYNMAN DIAGRAMS 2 u d s Some examples for diagrams emitting a W ±: W − W + e− νe u d And using quark mixing: W + u s To know the sign of the W -boson, we use charge conservation: the sum of the charges at the left hand side must equal the sum of the charges at the right hand side. -

Introduction to Supersymmetry
Introduction to Supersymmetry Pre-SUSY Summer School Corpus Christi, Texas May 15-18, 2019 Stephen P. Martin Northern Illinois University [email protected] 1 Topics: Why: Motivation for supersymmetry (SUSY) • What: SUSY Lagrangians, SUSY breaking and the Minimal • Supersymmetric Standard Model, superpartner decays Who: Sorry, not covered. • For some more details and a slightly better attempt at proper referencing: A supersymmetry primer, hep-ph/9709356, version 7, January 2016 • TASI 2011 lectures notes: two-component fermion notation and • supersymmetry, arXiv:1205.4076. If you find corrections, please do let me know! 2 Lecture 1: Motivation and Introduction to Supersymmetry Motivation: The Hierarchy Problem • Supermultiplets • Particle content of the Minimal Supersymmetric Standard Model • (MSSM) Need for “soft” breaking of supersymmetry • The Wess-Zumino Model • 3 People have cited many reasons why extensions of the Standard Model might involve supersymmetry (SUSY). Some of them are: A possible cold dark matter particle • A light Higgs boson, M = 125 GeV • h Unification of gauge couplings • Mathematical elegance, beauty • ⋆ “What does that even mean? No such thing!” – Some modern pundits ⋆ “We beg to differ.” – Einstein, Dirac, . However, for me, the single compelling reason is: The Hierarchy Problem • 4 An analogy: Coulomb self-energy correction to the electron’s mass A point-like electron would have an infinite classical electrostatic energy. Instead, suppose the electron is a solid sphere of uniform charge density and radius R. An undergraduate problem gives: 3e2 ∆ECoulomb = 20πǫ0R 2 Interpreting this as a correction ∆me = ∆ECoulomb/c to the electron mass: 15 0.86 10− meters m = m + (1 MeV/c2) × . -

Lecture 17 Highlights
Lecture 23 Highlights The phenomenon of Rabi oscillations is very different from our everyday experience of how macroscopic objects (i.e. those made up of many atoms) absorb electromagnetic radiation. When illuminated with light (like French fries at McDonalds) objects tend to steadily absorb the light and heat up to a steady state temperature, showing no signs of oscillation with time. We did a calculation of the transition probability of an atom illuminated with a broad spectrum of light and found that the probability increased linearly with time, leading to a constant transition rate. This difference comes about because the many absorption processes at different frequencies produce a ‘smeared-out’ response that destroys the coherent Rabi oscillations and results in a classical incoherent absorption. Selection Rules All of the transition probabilities are proportional to “dipole matrix elements,” such as x jn above. These are similar to dipole moment calculations for a charge distribution in classical physics, except that they involve the charge distribution in two different states, connected by the dipole operator for the transition. In many cases these integrals are zero because of symmetries of the associated wavefunctions. This gives rise to selection rules for possible transitions under the dipole approximation (atom size much smaller than the electromagnetic wave wavelength). For example, consider the matrix element z between states of the n,l , m ; n ', l ', m ' Hydrogen atom labeled by the quantum numbers n,,l m and n',','l m : z = ψ()()r z ψ r d3 r n,l , m ; n ', l ', m ' ∫∫∫ n,,l m n',l ', m ' To make progress, first consider just the φ integral. -

Introduction to Differential Equations
Quantum Dynamics – Quick View Concepts of primary interest: The Time-Dependent Schrödinger Equation Probability Density and Mixed States Selection Rules Transition Rates: The Golden Rule Sample Problem Discussions: Tools of the Trade Appendix: Classical E-M Radiation POSSIBLE ADDITIONS: After qualitative section, do the two state system, and then first and second order transitions (follow Fitzpatrick). Chain together the dipole rules to get l = 2,0,-2 and m = -2, -2, … , 2. ??Where do we get magnetic rules? Look at the canonical momentum and the Asquared term. Schrödinger, Erwin (1887-1961) Austrian physicist who invented wave mechanics in 1926. Wave mechanics was a formulation of quantum mechanics independent of Heisenberg's matrix mechanics. Like matrix mechanics, wave mechanics mathematically described the behavior of electrons and atoms. The central equation of wave mechanics is now known as the Schrödinger equation. Solutions to the equation provide probability densities and energy levels of systems. The time-dependent form of the equation describes the dynamics of quantum systems. http://scienceworld.wolfram.com/biography/Schroedinger.html © 1996-2006 Eric W. Weisstein www-history.mcs.st-andrews.ac.uk/Biographies/Schrodinger.html Quantum Dynamics: A Qualitative Introduction Introductory quantum mechanics focuses on time-independent problems leaving Contact: [email protected] dynamics to be discussed in the second term. Energy eigenstates are characterized by probability density distributions that are time-independent (static). There are examples of time-dependent behavior that are by demonstrated by rather simple introductory problems. In the case of a particle in an infinite well with the range [ 0 < x < a], the mixed state below exhibits time-dependence. -
![Arxiv:0901.3958V2 [Hep-Ph] 29 Jan 2009 Eul Rkn SU(2) Broken, Neously Information](https://docslib.b-cdn.net/cover/6459/arxiv-0901-3958v2-hep-ph-29-jan-2009-eul-rkn-su-2-broken-neously-information-1056459.webp)
Arxiv:0901.3958V2 [Hep-Ph] 29 Jan 2009 Eul Rkn SU(2) Broken, Neously Information
Gedanken Worlds without Higgs: QCD-Induced Electroweak Symmetry Breaking Chris Quigg1, 2 and Robert Shrock3 1Theoretical Physics Department Fermi National Accelerator Laboratory, Batavia, Illinois 60510 USA 2Institut f¨ur Theoretische Teilchenphysik Universit¨at Karlsruhe, D-76128 Karlsruhe, Germany 3C. N. Yang Institute for Theoretical Physics Stony Brook University, Stony Brook, New York 11794 USA To illuminate how electroweak symmetry breaking shapes the physical world, we investigate toy models in which no Higgs fields or other constructs are introduced to induce spontaneous symme- ⊗ ⊗ try breaking. Two models incorporate the standard SU(3)c SU(2)L U(1)Y gauge symmetry and fermion content similar to that of the standard model. The first class—like the standard elec- troweak theory—contains no bare mass terms, so the spontaneous breaking of chiral symmetry within quantum chromodynamics is the only source of electroweak symmetry breaking. The second class adds bare fermion masses sufficiently small that QCD remains the dominant source of elec- troweak symmetry breaking and the model can serve as a well-behaved low-energy effective field theory to energies somewhat above the hadronic scale. A third class of models is based on the left- ⊗ ⊗ ⊗ right–symmetric SU(3)c SU(2)L SU(2)R U(1)B−L gauge group. In a fourth class of models, built on SU(4)PS ⊗ SU(2)L ⊗ SU(2)R gauge symmetry, lepton number is treated as a fourth color. Many interesting characteristics of the models stem from the fact that the effective strength of the weak interactions is much closer to that of the residual strong interactions than in the real world.