Rotational Spectroscopy: the Rotation of Molecules

Total Page：16

File Type：pdf, Size：1020Kb

Rotational spectroscopy: The rotation of molecules z (IC) symmetric: ≠ ≠ IA=IB IC 0 x (IA) linear: IA=0; IB=IC asymmetric: ≠ ≠ ≠ IA IB IC 0 y (IB) Rotor in 3-D Nils Walter: Chem 260 ≠ spherical: IA=IB=IC 0 The moment of inertia for a diatomic (linear) rigid rotor r definition: r = r1 + r2 m1 m2 C(enter of mass) r1 r2 Moment of inertia: Balancing equation: m1r1 = m2r2 2 2 I = m1r1 + m2r2 m m ⇒ I = 1 2 r 2 = µr 2 µ = reduced mass + m1 m2 Nils Walter: Chem 260 Solution of the Schrödinger equation for the rigid diatomic rotor h2 (No potential, − V 2Ψ = EΨ µ only kinetic 2 energy) ⇒ EJ = hBJ(J+1); rot. quantum number J = 0,1,2,... h B = [Hz] 4πI ⇒ EJ+1 -EJ = 2hB(J+1) Nils Walter: Chem 260 Selection rules for the diatomic rotor: 1. Gross selection rule Light is a transversal electromagnetic wave a polar rotor appears to have an oscillating ⇒ a molecule must be polar to electric dipole Nils Walter: Chem 260 be able to interact with light Selection rules for the diatomic rotor: 2. Specific selection rule rotational quantum number J = 0,1,2,… describes the angular momentum of a molecule (just like electronic orbital quantum number l=0,1,2,...) and light behaves as a particle: photons have a spin of 1, i.e., an angular momentum of one unit and the total angular momentum upon absorption or emission of a photon has to be preserved ⇒⇒∆∆J = ± 1 Nils Walter: Chem 260 Okay, I know you are dying for it: Schrödinger also can explain the ∆J = ± 1 selection rule Transition dipole µ = Ψ µΨ dτ moment fi ∫ f i initial state final state ⇒ only if this integral is nonzero, the transition is allowed; if it is zero, the transition is forbidden Nils Walter: Chem 260 The angular momentum 1 E = Iω 2 P = Iω ⇒ P = 2EI 2 classical rotational classical angular momentum energy = + and EJ hBJ (J 1) m h J with B = π 4 I J=1 ⇒ P = J (J +1)h But P is a vector, i.e., has magnitude and direction Nils Walter: Chem 260 Degeneracy J=3 Energy only J=2 determined by J ⇓ all mJ = -J,…,+J m = mJ = J share the same energy ⇓ 2J+1 degeneracy ∆ ± Selection rule: mJ = 0, 1 Nils Walter: Chem 260 The allowed rotational transitions of a rigid linear rotor and their intensity ∆J = ±1 degenerate increasingly ∆ N − E 2J + 1 upper = e kT states Nlower Nils Walter: Chem 260 The non-rigid linear rotor rotor: Centrifugal forces elongate the bond and increase the moment of inertia ∆J = ±1 still holds! Nils Walter: Chem 260 The symmetric rotor = + + − 2 EJ ,K hBJ (J 1) h(A B)K h h A = B = π π 4 Ill 4 I⊥ J = 0,1,2,… K = J,J-1,…,-J Nils Walter: Chem 260.

Copy Link

Recommended publications

Vibrational-Rotational Spectroscopy ( )
Vibrational-Rotational Spectroscopy Vibrational-Rotational Spectrum of Heteronuclear Diatomic Absorption of mid-infrared light (~300-4000 cm-1): • Molecules can change vibrational and rotational states • Typically at room temperature, only ground vibrational state populated but several rotational levels may be populated. • Treating as harmonic oscillator and rigid rotor: subject to selection rules ∆v = ±1 and ∆J = ±1 EEEfield=∆ vib +∆ rot =ω =−EEfi = EvJEvJ()′,, ′ −( ′′ ′′ ) ω 11 vvvBJJvvBJJ==00()′′′′′′′′′ +++−++()11() () + 2πc 22 At room temperature, typically v=0′′ and ∆v = +1: ′ ′ ′′ ′′ vv=+0 BJJ() +−11 JJ( +) Now, since higher lying rotational levels can be populated, we can have: ∆=+J 1 JJ′′′=+1 vv= ++21 BJ( ′′ ) R − branch 0 P− branch ∆=−J 1 JJ′′′=−1 vv=−0 2 BJ′′ J’=4 J’=3 J’=1 v’=1 J’=0 P branch Q branch J’’=3 12B J’’=2 6B J’’=1 2B v’’=0 J’’=0 EJ” =0 2B 2B 4B 2B 2B 2B -6B -4B -2B +2B +4B +8B ν ν 0 By measuring absorption splittings, we can get B . From that, the bond length! In polyatomics, we can also have a Q branch, where ∆J0= and all transitions lie at ν=ν0 . This transition is allowed for perpendicular bands: ∂µ ∂q ⊥ to molecular symmetry axis. Intensity of Vibrational-Rotational Transitions There is generally no thermal population in upper (final) state (v’,J’) so intensity should scale as population of lower J state (J”). ∆=NNvJNvJ(,′ ′′′′′′′ ) − (, ) ≈ NJ ( ) NJ()′′∝− gJ ()exp( ′′ EJ′′ / kT ) =+()21exp(J′′ −hcBJ ′′() J ′′ + 1/) kT 5.33 Lecture Notes: Vibrational-Rotational Spectroscopy Page 2 Rotational Populations at Room Temperature for B = 5 cm-1 gJ'' thermal population NJ'' 0 5 10 15 20 Rotational Quantum Number J'' So, the vibrational-rotational spectrum should look like equally spaced lines about ν 0 with sidebands peaked at J’’>0.
[Show full text]
Optical Spectroscopy - Processes Monitored UV/ Fluorescence/ IR/ Raman/ Circular Dichroism
Time out—states and transitions Spectroscopy—transitions between energy states of a molecule excited by absorption or emission of a photon hν = ∆E = Ei -Ef Energy levels due to interactions between parts of molecule (atoms, electrons and nucleii) as described by quantum mechanics, and are characteristic of components involved, i.e. electron distributions (orbitals), bond strengths and types plus molecular geometries and atomic masses involved Spectroscopic Regions Typical wavelength Approximate energy Spectroscopic region Techniques and Applications (cm) (kcal mole-1) -11 8 10 3 x 10 γ-ray MÖssbauer 10-8 3 x 105 X-ray x-ray diffraction, scattering 10-5 3 x 102 Vacuum UV Electronic Spectra 3 x 10-5 102 Near UV Electronic Spectra 6 x 10-5 5 x 103 Visible Electronic Spectra 10-3 3 x 100 IR Vibrational Spectra 10-2 3 x 10-1 Far IR Vibrational Spectra 10-1 3 x 10-2 Microwave Rotational Spectra 100 3 x 10-3 Microwave Electron paramagnetic resonance 10 3 x 10-4 Radio frequency Nuclear magnetic resonance Adapted from Table 7-1; Biophysical Chemistry, Part II by Cantor and Schimmel Spectroscopic Process • Molecules contain distribution of charges (electrons and nuclei, charges from protons) and spins which is dynamically changed when molecule is exposed to light •In a spectroscopic experiment, light is used to probe a sample. What we seek to understand is: – the RATE at which the molecule responds to this perturbation (this is the response or spectral intensity) – why only certain wavelengths cause changes (this is the spectrum, the wavelength dependence of the response) – the process by which the molecule alters the radiation that emerges from the sample (absorption, scattering, fluorescence, photochemistry, etc.) so we can detect it These tell us about molecular identity, structure, mechanisms and analytical concentrations Magnetic Resonance—different course • Long wavelength radiowaves are of low energy that is sufficient to ‘flip’ the spin of nuclei in a magnetic field (NMR).
[Show full text]
Rotational Spectroscopy and Interstellar Molecules
Volume -5, Issue-2, April 2015 » Plescia, J. B., and Cintala M. J. (2012), Impact melt Rotational Spectroscopy and Interstellar in small lunar highland craters, J. Geophys. Res., 117, Molecules E00H12,doi:10.1029/2011JE003941 » Plescia J.B. and Spudis P.D. (2014) Impact melt flows at The fact that life exists on Earth is no secret. However, Lowell crater, Planetary and Space Science, 103, 219- understanding the origin of life, its evolution, and the fu- 227 ture of life on Earth remain interesting issues to be ad- » Shkuratov, Y.,Kaydash, V.,Videen, G. (2012)The lunar dressed. That the regions between stars contain by far the crater Giordano Bruno as seen with optical roughness largest reservoir of chemically-bonded matter in nature imagery, Icarus, 218(1), 525-533 obviously demonstrates the importance of chemistry in » Smrekar S. and Pieters C.M. (1985) Near-infrared spec- the interstellar space. The unique detection of over 200 troscopy of probable impact melt from three large lunar different interstellar molecules largely via their rotational highland craters, Icarus, 63, 442-452 spectra has laid to rest the popular perception that the » Srivastava, N., Kumar, D., Gupta, R. P., 2013. Young vastness of space is an empty vacuum dotted with stars, viscous flows in the Lowell crater of Orientale basin, planets, black holes, and other celestial formations. As- Moon: Impact melts or volcanic eruptions? Planetary trochemistry comprises observations, theory and experi- and Space Science, 87, 37-45. ments aimed at understanding the formation of molecules » Stopar J. D., Hawke B. R., Robinson M. S., DeneviB.W., and matter in the Universe i.e.
[Show full text]
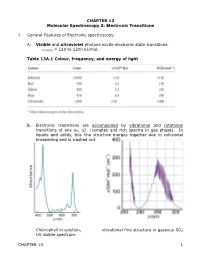
CHAPTER 13 Molecular Spectroscopy 2: Electronic Transitions
CHAPTER 13 Molecular Spectroscopy 2: Electronic Transitions I. General Features of Electronic spectroscopy. A. Visible and ultraviolet photons excite electronic state transitions. εphoton = 120 to 1200 kJ/mol. Table 13A.1 Colour, frequency, and energy of light B. Electronic transitions are accompanied by vibrational and rotational transitions of any Δν, ΔJ (complex and rich spectra in gas phase). In liquids and solids, this fine structure merges together due to collisional broadening and is washed out. Chlorophyll in solution, vibrational fine structure in gaseous SO2 UV visible spectrum. CHAPTER 13 1 C. Molecules need not have permanent dipole to undergo electronic transitions. All that is required is a redistribution of electronic and nuclear charge between the initial and final electronic state. Transition intensity ~ |µ|2 where µ is the magnitude of the transition dipole moment given by: ˆ d µ = ∫ ψfinalµψ initial τ where µˆ = −e ∑ri + e ∑Ziri € electrons nuclei r vector position of the particle i = D. Franck-Condon principle: Because nuclei are so much more massive and € sluggish than electrons, electronic transitions can happen much faster than the nuclei can respond. Electronic transitions occur vertically on energy diagram at right. (Hence the name vertical transition) Transition probability depends on vibrational wave function overlap (Franck-Condon factor). In this example: ν = 0 ν’ = 0 have small overlap ν = 0 ν’ = 2 have greatest overlap Now because the total molecular wavefunction can be approximately factored into 2 terms, electronic wavefunction and the nuclear position wavefunction (using Born-Oppenheimer approx.) the transition dipole can also be factored into 2 terms also: S µ = µelectronic i,f S d Franck Condon factor i,j i,f = ∫ ψf,vibr ψi,vibr τ = − CHAPTER 13 2 See derivation “Justification 14.2” II.
[Show full text]
Rotational Spectroscopy
Applied Spectroscopy Rotational Spectroscopy Recommended Reading: 1. Banwell and McCash: Chapter 2 2. Atkins: Chapter 16, sections 4 - 8 Aims In this section you will be introduced to 1) Rotational Energy Levels (term values) for diatomic molecules and linear polyatomic molecules 2) The rigid rotor approximation 3) The effects of centrifugal distortion on the energy levels 4) The Principle Moments of Inertia of a molecule. 5) Definitions of symmetric , spherical and asymmetric top molecules. 6) Experimental methods for measuring the pure rotational spectrum of a molecule Microwave Spectroscopy - Rotation of Molecules Microwave Spectroscopy is concerned with transitions between rotational energy levels in molecules. Definition d Electric Dipole: p = q.d +q -q p H Most heteronuclear molecules possess Cl a permanent dipole moment -q +q e.g HCl, NO, CO, H2O... p Molecules can interact with electromagnetic radiation, absorbing or emitting a photon of frequency ω, if they possess an electric dipole moment p, oscillating at the same frequency Gross Selection Rule: A molecule has a rotational spectrum only if it has a permanent dipole moment. Rotating molecule _ _ + + t _ + _ + dipole momentp dipole Homonuclear molecules (e.g. O2, H2, Cl2, Br2…. do not have a permanent dipole moment and therefore do not have a microwave spectrum! General features of rotating systems m Linear velocity v angular velocity v = distance ω = radians O r time time v = ω × r Moment of Inertia I = mr2. A molecule can have three different moments of inertia IA, IB and IC about orthogonal axes a, b and c. 2 I = ∑miri i R Note how ri is defined, it is the perpendicular distance from axis of rotation ri Rigid Diatomic Rotors ro IB = Ic, and IA = 0.
[Show full text]
Photoionization Spectroscopy O
Photoionization spectroscopy of CH3C3N in the vacuum-ultraviolet range N. Lamarre, C. Falvo, C. Alcaraz, B. Cunha de Miranda, S. Douin, A. Flütsch, C. Romanzin, J.-C. Guillemin, Séverine Boyé-Péronne, B. Gans To cite this version: N. Lamarre, C. Falvo, C. Alcaraz, B. Cunha de Miranda, S. Douin, et al.. Photoionization spectroscopy of CH3C3N in the vacuum-ultraviolet range. Journal of Molecular Spectroscopy, Elsevier, 2015, 315, pp.206-216. 10.1016/j.jms.2015.03.005. hal-01138635 HAL Id: hal-01138635 https://hal-univ-rennes1.archives-ouvertes.fr/hal-01138635 Submitted on 4 Nov 2015 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Photoionization spectroscopy of CH 3C3N in the vacuum-ultraviolet range N. Lamarre a, C. Falvo a, C. Alcaraz b,c, B. Cunha de Miranda b, S. Douin a, A. Fl utsch¨ a, C. Romanzin b, J.-C. Guillemin d, a, a, S. Boy e-P´ eronne´ ∗, B. Gans ∗ aInstitut des Sciences Mol´eculaires d’Orsay, Univ Paris-Sud; CNRS, bat 210, Univ Paris-Sud 91405 Orsay cedex (France) bLaboratoire de Chimie Physique, Univ Paris-Sud; CNRS UMR 8000, bat 350, Univ Paris-Sud 91405 Orsay cedex (France) cSynchrotron SOLEIL, L'Orme des Merisiers, St.
[Show full text]
Lecture B4 Vibrational Spectroscopy, Part 2 Quantum Mechanical SHO
Lecture B4 Vibrational Spectroscopy, Part 2 Quantum Mechanical SHO. WHEN we solve the Schrödinger equation, we always obtain two things: 1. a set of eigenstates, |ψn>. 2. a set of eigenstate energies, En QM predicts the existence of discrete, evenly spaced, vibrational energy levels for the SHO. n = 0,1,2,3... For the ground state (n=0), E = ½hν. Notes: This is called the zero point energy. Optical selection rule -- SHO can absorb or emit light with a ∆n = ±1 The IR absorption spectrum for a diatomic molecule, such as HCl: diatomic Optical selection rule 1 -- SHO can absorb or emit light with a ∆n = ±1 Optical selection rule 2 -- a change in molecular dipole moment (∆μ/∆x) must occur with the vibrational motion. (Note: μ here means dipole moment). If a more realistic Morse potential is used in the Schrödinger Equation, these energy levels get scrunched together... ΔE=hν ΔE<hν The vibrational spectroscopy of polyatomic molecules gets more interesting... For diatomic or linear molecules: 3N-5 modes For nonlinear molecules: 3N-6 modes N = number of atoms in molecule The vibrational spectroscopy of polyatomic molecules gets more interesting... Optical selection rule 1 -- SHO can absorb or emit light with a ∆n = ±1 Optical selection rule 2 -- a change in molecular dipole moment (∆μ/∆x) must occur with the vibrational motion of a mode. Consider H2O (a nonlinear molecule): 3N-6 = 3(3)-6 = 3 Optical selection rule 2 -- a change in molecular dipole moment (∆μ/∆x) must occur with the vibrational motion of a mode. Consider H2O (a nonlinear molecule): 3N-6 = 3(3)-6 = 3 All bands are observed in the IR spectrum.
[Show full text]
Hydrogen Conversion in Nanocages
Review Hydrogen Conversion in Nanocages Ernest Ilisca Laboratoire Matériaux et Phénomènes Quantiques, Université de Paris, CNRS, F-75013 Paris, France; [email protected] Abstract: Hydrogen molecules exist in the form of two distinct isomers that can be interconverted by physical catalysis. These ortho and para forms have different thermodynamical properties. Over the last century, the catalysts developed to convert hydrogen from one form to another, in laboratories and industries, were magnetic and the interpretations relied on magnetic dipolar interactions. The variety concentration of a sample and the conversion rates induced by a catalytic action were mostly measured by thermal methods related to the diffusion of the o-p reaction heat. At the turning of the new century, the nature of the studied catalysts and the type of measures and motivations completely changed. Catalysts investigated now are non-magnetic and new spectroscopic measurements have been developed. After a fast survey of the past studies, the review details the spectroscopic methods, emphasizing their originalities, performances and reﬁnements: how Infra-Red measurements charac- terize the catalytic sites and follow the conversion in real-time, Ultra-Violet irradiations explore the electronic nature of the reaction and hyper-frequencies driving the nuclear spins. The new catalysts, metallic or insulating, are detailed to display the operating electronic structure. New electromagnetic mechanisms, involving energy and momenta transfers, are discovered providing a classiﬁcation frame for the newly observed reactions. Keywords: molecular spectroscopy; nanocages; electronic excitations; nuclear magnetism Citation: Ilisca, E. Hydrogen Conversion in Nanocages. Hydrogen The intertwining of quantum, spectroscopic and thermodynamical properties of the 2021, 2, 160–206.
[Show full text]
Rotational Spectroscopy
Rotational spectroscopy - Involve transitions between rotational states of the molecules (gaseous state!) - Energy difference between rotational levels of molecules has the same order of magnitude with microwave energy - Rotational spectroscopy is called pure rotational spectroscopy, to distinguish it from roto-vibrational spectroscopy (the molecule changes its state of vibration and rotation simultaneously) and vibronic spectroscopy (the molecule changes its electronic state and vibrational state simultaneously) Molecules do not rotate around an arbitrary axis! Generally, the rotation is around the mass center of the molecule. The rotational axis must allow the conservation of M R α pα const kinetic angular momentum. α Rotational spectroscopy Rotation of diatomic molecule - Classical description Diatomic molecule = a system formed by 2 different masses linked together with a rigid connector (rigid rotor = the bond length is assumed to be fixed!). The system rotation around the mass center is equivalent with the rotation of a particle with the mass μ (reduced mass) around the center of mass. 2 2 2 2 m1m2 2 The moment of inertia: I miri m1r1 m2r2 R R i m1 m2 Moment of inertia (I) is the rotational equivalent of mass (m). Angular velocity () is the equivalent of linear velocity (v). Er → rotational kinetic energy L = I → angular momentum mv 2 p2 Iω2 L2 E E c 2 2m r 2 2I Quantum rotation: The diatomic rigid rotor The rigid rotor represents the quantum mechanical “particle on a sphere” problem: Rotational energy is purely
[Show full text]
Lecture 17 Highlights
Lecture 23 Highlights The phenomenon of Rabi oscillations is very different from our everyday experience of how macroscopic objects (i.e. those made up of many atoms) absorb electromagnetic radiation. When illuminated with light (like French fries at McDonalds) objects tend to steadily absorb the light and heat up to a steady state temperature, showing no signs of oscillation with time. We did a calculation of the transition probability of an atom illuminated with a broad spectrum of light and found that the probability increased linearly with time, leading to a constant transition rate. This difference comes about because the many absorption processes at different frequencies produce a ‘smeared-out’ response that destroys the coherent Rabi oscillations and results in a classical incoherent absorption. Selection Rules All of the transition probabilities are proportional to “dipole matrix elements,” such as x jn above. These are similar to dipole moment calculations for a charge distribution in classical physics, except that they involve the charge distribution in two different states, connected by the dipole operator for the transition. In many cases these integrals are zero because of symmetries of the associated wavefunctions. This gives rise to selection rules for possible transitions under the dipole approximation (atom size much smaller than the electromagnetic wave wavelength). For example, consider the matrix element z between states of the n,l , m ; n ', l ', m ' Hydrogen atom labeled by the quantum numbers n,,l m and n',','l m : z = ψ()()r z ψ r d3 r n,l , m ; n ', l ', m ' ∫∫∫ n,,l m n',l ', m ' To make progress, first consider just the φ integral.
[Show full text]
Fine-And Hyperfine-Structure Effects in Molecular Photoionization: I
Fine- and hyperfine-structure effects in molecular photoionization: I. General theory and direct photoionization Matthias Germann1 and Stefan Willitsch1, a) Department of Chemistry, University of Basel, Klingelbergstrasse 80, 4056 Basel, Switzerland (Dated: 2 October 2018) We develop a model for predicting fine- and hyperfine intensities in the direct photoionization of molecules based on the separability of electron and nuclear spin states from vibrational-electronic states. Using spherical tensor algebra, we derive highly symmetrized forms of the squared photoionization dipole matrix elements from which which we derive the salient selection and propensity rules for fine- and hyperfine resolved photoionizing transitions. Our theoretical results are validated by the analysis of the fine-structure resolved photoelectron spectrum of O2 (reported by H. Palm and F. Merkt, Phys. Rev. Lett. 81, 1385 (1998)) and are used for predicting hyperfine populations of molecular ions produced by photoionization. I. INTRODUCTION dynamics.19–21 Thus, there is a growing need for theo- retical models capable of describing fine- and hyperfine Photoionization and photoelectron spectroscopy are effects in molecular photoionization. Whereas the hy- among the eminent experimental techniques to gain infor- perfine structure in Rydberg spectra has previously been mation on the electronic structure of molecules, on their treated within the framework of multichannel quantum- 14–18 photoionization dynamics and the structure and dynam- defect theory (MQDT), we are not aware of
[Show full text]
Introduction to Differential Equations
Quantum Dynamics – Quick View Concepts of primary interest: The Time-Dependent Schrödinger Equation Probability Density and Mixed States Selection Rules Transition Rates: The Golden Rule Sample Problem Discussions: Tools of the Trade Appendix: Classical E-M Radiation POSSIBLE ADDITIONS: After qualitative section, do the two state system, and then first and second order transitions (follow Fitzpatrick). Chain together the dipole rules to get l = 2,0,-2 and m = -2, -2, … , 2. ??Where do we get magnetic rules? Look at the canonical momentum and the Asquared term. Schrödinger, Erwin (1887-1961) Austrian physicist who invented wave mechanics in 1926. Wave mechanics was a formulation of quantum mechanics independent of Heisenberg's matrix mechanics. Like matrix mechanics, wave mechanics mathematically described the behavior of electrons and atoms. The central equation of wave mechanics is now known as the Schrödinger equation. Solutions to the equation provide probability densities and energy levels of systems. The time-dependent form of the equation describes the dynamics of quantum systems. http://scienceworld.wolfram.com/biography/Schroedinger.html © 1996-2006 Eric W. Weisstein www-history.mcs.st-andrews.ac.uk/Biographies/Schrodinger.html Quantum Dynamics: A Qualitative Introduction Introductory quantum mechanics focuses on time-independent problems leaving Contact: [email protected] dynamics to be discussed in the second term. Energy eigenstates are characterized by probability density distributions that are time-independent (static). There are examples of time-dependent behavior that are by demonstrated by rather simple introductory problems. In the case of a particle in an infinite well with the range [ 0 < x < a], the mixed state below exhibits time-dependence.
[Show full text]