Simple Linear Regression Least Squares Estimates of Β0 and Β1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Simple Linear Regression with Least Square Estimation: an Overview
Aditya N More et al, / (IJCSIT) International Journal of Computer Science and Information Technologies, Vol. 7 (6) , 2016, 2394-2396 Simple Linear Regression with Least Square Estimation: An Overview Aditya N More#1, Puneet S Kohli*2, Kshitija H Kulkarni#3 #1-2Information Technology Department,#3 Electronics and Communication Department College of Engineering Pune Shivajinagar, Pune – 411005, Maharashtra, India Abstract— Linear Regression involves modelling a relationship amongst dependent and independent variables in the form of a (2.1) linear equation. Least Square Estimation is a method to determine the constants in a Linear model in the most accurate way without much complexity of solving. Metrics where such as Coefficient of Determination and Mean Square Error is the ith value of the sample data point determine how good the estimation is. Statistical Packages is the ith value of y on the predicted regression such as R and Microsoft Excel have built in tools to perform Least Square Estimation over a given data set. line The above equation can be geometrically depicted by Keywords— Linear Regression, Machine Learning, Least Squares Estimation, R programming figure 2.1. If we draw a square at each point whose length is equal to the absolute difference between the sample data point and the predicted value as shown, each of the square would then represent the residual error in placing the I. INTRODUCTION regression line. The aim of the least square method would Linear Regression involves establishing linear be to place the regression line so as to minimize the sum of relationships between dependent and independent variables. -

Generalized Linear Models
Generalized Linear Models Advanced Methods for Data Analysis (36-402/36-608) Spring 2014 1 Generalized linear models 1.1 Introduction: two regressions • So far we've seen two canonical settings for regression. Let X 2 Rp be a vector of predictors. In linear regression, we observe Y 2 R, and assume a linear model: T E(Y jX) = β X; for some coefficients β 2 Rp. In logistic regression, we observe Y 2 f0; 1g, and we assume a logistic model (Y = 1jX) log P = βT X: 1 − P(Y = 1jX) • What's the similarity here? Note that in the logistic regression setting, P(Y = 1jX) = E(Y jX). Therefore, in both settings, we are assuming that a transformation of the conditional expec- tation E(Y jX) is a linear function of X, i.e., T g E(Y jX) = β X; for some function g. In linear regression, this transformation was the identity transformation g(u) = u; in logistic regression, it was the logit transformation g(u) = log(u=(1 − u)) • Different transformations might be appropriate for different types of data. E.g., the identity transformation g(u) = u is not really appropriate for logistic regression (why?), and the logit transformation g(u) = log(u=(1 − u)) not appropriate for linear regression (why?), but each is appropriate in their own intended domain • For a third data type, it is entirely possible that transformation neither is really appropriate. What to do then? We think of another transformation g that is in fact appropriate, and this is the basic idea behind a generalized linear model 1.2 Generalized linear models • Given predictors X 2 Rp and an outcome Y , a generalized linear model is defined by three components: a random component, that specifies a distribution for Y jX; a systematic compo- nent, that relates a parameter η to the predictors X; and a link function, that connects the random and systematic components • The random component specifies a distribution for the outcome variable (conditional on X). -

Lecture 18: Regression in Practice
Regression in Practice Regression in Practice ● Regression Errors ● Regression Diagnostics ● Data Transformations Regression Errors Ice Cream Sales vs. Temperature Image source Linear Regression in R > summary(lm(sales ~ temp)) Call: lm(formula = sales ~ temp) Residuals: Min 1Q Median 3Q Max -74.467 -17.359 3.085 23.180 42.040 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -122.988 54.761 -2.246 0.0513 . temp 28.427 2.816 10.096 3.31e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 35.07 on 9 degrees of freedom Multiple R-squared: 0.9189, Adjusted R-squared: 0.9098 F-statistic: 101.9 on 1 and 9 DF, p-value: 3.306e-06 Some Goodness-of-fit Statistics ● Residual standard error ● R2 and adjusted R2 ● F statistic Anatomy of Regression Errors Image Source Residual Standard Error ● A residual is a difference between a fitted value and an observed value. ● The total residual error (RSS) is the sum of the squared residuals. ○ Intuitively, RSS is the error that the model does not explain. ● It is a measure of how far the data are from the regression line (i.e., the model), on average, expressed in the units of the dependent variable. ● The standard error of the residuals is roughly the square root of the average residual error (RSS / n). ○ Technically, it’s not √(RSS / n), it’s √(RSS / (n - 2)); it’s adjusted by degrees of freedom. R2: Coefficient of Determination ● R2 = ESS / TSS ● Interpretations: ○ The proportion of the variance in the dependent variable that the model explains. -

Chapter 2 Simple Linear Regression Analysis the Simple
Chapter 2 Simple Linear Regression Analysis The simple linear regression model We consider the modelling between the dependent and one independent variable. When there is only one independent variable in the linear regression model, the model is generally termed as a simple linear regression model. When there are more than one independent variables in the model, then the linear model is termed as the multiple linear regression model. The linear model Consider a simple linear regression model yX01 where y is termed as the dependent or study variable and X is termed as the independent or explanatory variable. The terms 0 and 1 are the parameters of the model. The parameter 0 is termed as an intercept term, and the parameter 1 is termed as the slope parameter. These parameters are usually called as regression coefficients. The unobservable error component accounts for the failure of data to lie on the straight line and represents the difference between the true and observed realization of y . There can be several reasons for such difference, e.g., the effect of all deleted variables in the model, variables may be qualitative, inherent randomness in the observations etc. We assume that is observed as independent and identically distributed random variable with mean zero and constant variance 2 . Later, we will additionally assume that is normally distributed. The independent variables are viewed as controlled by the experimenter, so it is considered as non-stochastic whereas y is viewed as a random variable with Ey()01 X and Var() y 2 . Sometimes X can also be a random variable. -

1 Simple Linear Regression I – Least Squares Estimation
1 Simple Linear Regression I – Least Squares Estimation Textbook Sections: 18.1–18.3 Previously, we have worked with a random variable x that comes from a population that is normally distributed with mean µ and variance σ2. We have seen that we can write x in terms of µ and a random error component ε, that is, x = µ + ε. For the time being, we are going to change our notation for our random variable from x to y. So, we now write y = µ + ε. We will now find it useful to call the random variable y a dependent or response variable. Many times, the response variable of interest may be related to the value(s) of one or more known or controllable independent or predictor variables. Consider the following situations: LR1 A college recruiter would like to be able to predict a potential incoming student’s first–year GPA (y) based on known information concerning high school GPA (x1) and college entrance examination score (x2). She feels that the student’s first–year GPA will be related to the values of these two known variables. LR2 A marketer is interested in the effect of changing shelf height (x1) and shelf width (x2)on the weekly sales (y) of her brand of laundry detergent in a grocery store. LR3 A psychologist is interested in testing whether the amount of time to become proficient in a foreign language (y) is related to the child’s age (x). In each case we have at least one variable that is known (in some cases it is controllable), and a response variable that is a random variable. -

Linear Regression Using Stata (V.6.3)
Linear Regression using Stata (v.6.3) Oscar Torres-Reyna [email protected] December 2007 http://dss.princeton.edu/training/ Regression: a practical approach (overview) We use regression to estimate the unknown effect of changing one variable over another (Stock and Watson, 2003, ch. 4) When running a regression we are making two assumptions, 1) there is a linear relationship between two variables (i.e. X and Y) and 2) this relationship is additive (i.e. Y= x1 + x2 + …+xN). Technically, linear regression estimates how much Y changes when X changes one unit. In Stata use the command regress, type: regress [dependent variable] [independent variable(s)] regress y x In a multivariate setting we type: regress y x1 x2 x3 … Before running a regression it is recommended to have a clear idea of what you are trying to estimate (i.e. which are your outcome and predictor variables). A regression makes sense only if there is a sound theory behind it. 2 PU/DSS/OTR Regression: a practical approach (setting) Example: Are SAT scores higher in states that spend more money on education controlling by other factors?* – Outcome (Y) variable – SAT scores, variable csat in dataset – Predictor (X) variables • Per pupil expenditures primary & secondary (expense) • % HS graduates taking SAT (percent) • Median household income (income) • % adults with HS diploma (high) • % adults with college degree (college) • Region (region) *Source: Data and examples come from the book Statistics with Stata (updated for version 9) by Lawrence C. Hamilton (chapter 6). Click here to download the data or search for it at http://www.duxbury.com/highered/. -

Linear Regression in Matrix Form
Statistics 512: Applied Linear Models Topic 3 Topic Overview This topic will cover • thinking in terms of matrices • regression on multiple predictor variables • case study: CS majors • Text Example (KNNL 236) Chapter 5: Linear Regression in Matrix Form The SLR Model in Scalar Form iid 2 Yi = β0 + β1Xi + i where i ∼ N(0,σ ) Consider now writing an equation for each observation: Y1 = β0 + β1X1 + 1 Y2 = β0 + β1X2 + 2 . Yn = β0 + β1Xn + n TheSLRModelinMatrixForm Y1 β0 + β1X1 1 Y2 β0 + β1X2 2 . = . + . . . . Yn β0 + β1Xn n Y X 1 1 1 1 Y X 2 1 2 β0 2 . = . + . . . β1 . Yn 1 Xn n (I will try to use bold symbols for matrices. At first, I will also indicate the dimensions as a subscript to the symbol.) 1 • X is called the design matrix. • β is the vector of parameters • is the error vector • Y is the response vector The Design Matrix 1 X1 1 X2 Xn×2 = . . 1 Xn Vector of Parameters β0 β2×1 = β1 Vector of Error Terms 1 2 n×1 = . . n Vector of Responses Y1 Y2 Yn×1 = . . Yn Thus, Y = Xβ + Yn×1 = Xn×2β2×1 + n×1 2 Variance-Covariance Matrix In general, for any set of variables U1,U2,... ,Un,theirvariance-covariance matrix is defined to be 2 σ {U1} σ{U1,U2} ··· σ{U1,Un} . σ{U ,U } σ2{U } ... σ2{ } 2 1 2 . U = . . .. .. σ{Un−1,Un} 2 σ{Un,U1} ··· σ{Un,Un−1} σ {Un} 2 where σ {Ui} is the variance of Ui,andσ{Ui,Uj} is the covariance of Ui and Uj. -
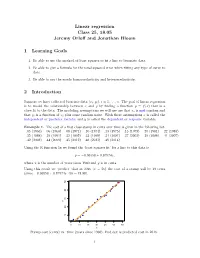
Reading 25: Linear Regression
Linear regression Class 25, 18.05 Jeremy Orloff and Jonathan Bloom 1 Learning Goals 1. Be able to use the method of least squares to fit a line to bivariate data. 2. Be able to give a formula for the total squared error when fitting any type of curve to data. 3. Be able to say the words homoscedasticity and heteroscedasticity. 2 Introduction Suppose we have collected bivariate data (xi; yi), i = 1; : : : ; n. The goal of linear regression is to model the relationship between x and y by finding a function y = f(x) that is a close fit to the data. The modeling assumptions we will use are that xi is not random and that yi is a function of xi plus some random noise. With these assumptions x is called the independent or predictor variable and y is called the dependent or response variable. Example 1. The cost of a first class stamp in cents over time is given in the following list. .05 (1963) .06 (1968) .08 (1971) .10 (1974) .13 (1975) .15 (1978) .20 (1981) .22 (1985) .25 (1988) .29 (1991) .32 (1995) .33 (1999) .34 (2001) .37 (2002) .39 (2006) .41 (2007) .42 (2008) .44 (2009) .45 (2012) .46 (2013) .49 (2014) Using the R function lm we found the ‘least squares fit’ for a line to this data is y = −0:06558 + 0:87574x; where x is the number of years since 1960 and y is in cents. Using this result we ‘predict’ that in 2016 (x = 56) the cost of a stamp will be 49 cents (since −0:06558 + 0:87574x · 56 = 48:98). -

Lecture 2: Linear Regression
Lecture 2: Linear regression Roger Grosse 1 Introduction Let's jump right in and look at our first machine learning algorithm, linear regression. In regression, we are interested in predicting a scalar-valued target, such as the price of a stock. By linear, we mean that the target must be predicted as a linear function of the inputs. This is a kind of supervised learning algorithm; recall that, in supervised learning, we have a collection of training examples labeled with the correct outputs. Regression is an important problem in its own right. But today's dis- cussion will also highlight a number of themes which will recur throughout the course: • Formulating a machine learning task mathematically as an optimiza- tion problem. • Thinking about the data points and the model parameters as vectors. • Solving the optimization problem using two different strategies: deriv- ing a closed-form solution, and applying gradient descent. These two strategies are how we will derive nearly all of the learning algorithms in this course. • Writing the algorithm in terms of linear algebra, so that we can think about it more easily and implement it efficiently in a high-level pro- gramming language. • Making a linear algorithm more powerful using basis functions, or features. • Analyzing the generalization performance of an algorithm, and in par- ticular the problems of overfitting and underfitting. 1.1 Learning goals • Know what objective function is used in linear regression, and how it is motivated. • Derive both the closed-form solution and the gradient descent updates for linear regression. • Write both solutions in terms of matrix and vector operations. -

Chapter 11 Autocorrelation
Chapter 11 Autocorrelation One of the basic assumptions in the linear regression model is that the random error components or disturbances are identically and independently distributed. So in the model y Xu , it is assumed that 2 u ifs 0 Eu(,tts u ) 0 if0s i.e., the correlation between the successive disturbances is zero. 2 In this assumption, when Eu(,tts u ) u , s 0 is violated, i.e., the variance of disturbance term does not remain constant, then the problem of heteroskedasticity arises. When Eu(,tts u ) 0, s 0 is violated, i.e., the variance of disturbance term remains constant though the successive disturbance terms are correlated, then such problem is termed as the problem of autocorrelation. When autocorrelation is present, some or all off-diagonal elements in E(')uu are nonzero. Sometimes the study and explanatory variables have a natural sequence order over time, i.e., the data is collected with respect to time. Such data is termed as time-series data. The disturbance terms in time series data are serially correlated. The autocovariance at lag s is defined as sttsEu( , u ); s 0, 1, 2,... At zero lag, we have constant variance, i.e., 22 0 Eu()t . The autocorrelation coefficient at lag s is defined as Euu()tts s s ;s 0,1,2,... Var() utts Var ( u ) 0 Assume s and s are symmetrical in s , i.e., these coefficients are constant over time and depend only on the length of lag s . The autocorrelation between the successive terms (and)uu21, (and),....uu32 (and)uunn1 gives the autocorrelation of order one, i.e., 1 . -

A Bayesian Treatment of Linear Gaussian Regression
A Bayesian Treatment of Linear Gaussian Regression Frank Wood December 3, 2009 Bayesian Approach to Classical Linear Regression In classical linear regression we have the following model yjβ; σ2; X ∼ N(Xβ; σ2I) Unfortunately we often don't know the observation error σ2 and, as well, we don't know the vector of linear weights β that relates the input(s) to the output. In Bayesian regression, we are interested in several inference objectives. One is the posterior distribution of the model parameters, in particular the posterior distribution of the observation error variance given the inputs and the outputs. P(σ2jX; y) Posterior Distribution of the Error Variance Of course in order to derive P(σ2jX; y) We have to treat β as a nuisance parameter and integrate it out Z P(σ2jX; y) = P(σ2; βjX; y)dβ Z = P(σ2jβ; X; y)P(βjX; y)dβ Predicting a New Output for a (set of) new Input(s) Of particular interest is the ability to predict the distribution of output values for a new input P(ynew jX; y; Xnew ) Here we have to treat both σ2 and β as a nuisance parameters and integrate them out P(ynew jX; y; Xnew ) ZZ 2 2 2 = P(ynew jβ; σ )P(σ jβ; X; y)P(βjX; y)dβ; dσ Noninformative Prior for Classical Regression For both objectives, we need to place a prior on the model parameters σ2 and β. We will choose a noninformative prior to demonstrate the connection between the Bayesian approach to multiple regression and the classical approach. -
Linear Regression and Correlation
NCSS Statistical Software NCSS.com Chapter 300 Linear Regression and Correlation Introduction Linear Regression refers to a group of techniques for fitting and studying the straight-line relationship between two variables. Linear regression estimates the regression coefficients β0 and β1 in the equation Yj = β0 + β1 X j + ε j where X is the independent variable, Y is the dependent variable, β0 is the Y intercept, β1 is the slope, and ε is the error. In order to calculate confidence intervals and hypothesis tests, it is assumed that the errors are independent and normally distributed with mean zero and variance σ 2 . Given a sample of N observations on X and Y, the method of least squares estimates β0 and β1 as well as various other quantities that describe the precision of the estimates and the goodness-of-fit of the straight line to the data. Since the estimated line will seldom fit the data exactly, a term for the discrepancy between the actual and fitted data values must be added. The equation then becomes y j = b0 + b1x j + e j = y j + e j 300-1 © NCSS, LLC. All Rights Reserved. NCSS Statistical Software NCSS.com Linear Regression and Correlation where j is the observation (row) number, b0 estimates β0 , b1 estimates β1 , and e j is the discrepancy between the actual data value y j and the fitted value given by the regression equation, which is often referred to as y j . This discrepancy is usually referred to as the residual. Note that the linear regression equation is a mathematical model describing the relationship between X and Y.