A Historical Review of the Discovery of the Quark and Gluon Jets
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1.1. Introduction the Phenomenon of Positron Annihilation Spectroscopy
PRINCIPLES OF POSITRON ANNIHILATION Chapter-1 __________________________________________________________________________________________ 1.1. Introduction The phenomenon of positron annihilation spectroscopy (PAS) has been utilized as nuclear method to probe a variety of material properties as well as to research problems in solid state physics. The field of solid state investigation with positrons started in the early fifties, when it was recognized that information could be obtained about the properties of solids by studying the annihilation of a positron and an electron as given by Dumond et al. [1] and Bendetti and Roichings [2]. In particular, the discovery of the interaction of positrons with defects in crystal solids by Mckenize et al. [3] has given a strong impetus to a further elaboration of the PAS. Currently, PAS is amongst the best nuclear methods, and its most recent developments are documented in the proceedings of the latest positron annihilation conferences [4-8]. PAS is successfully applied for the investigation of electron characteristics and defect structures present in materials, magnetic structures of solids, plastic deformation at low and high temperature, and phase transformations in alloys, semiconductors, polymers, porous material, etc. Its applications extend from advanced problems of solid state physics and materials science to industrial use. It is also widely used in chemistry, biology, and medicine (e.g. locating tumors). As the process of measurement does not mostly influence the properties of the investigated sample, PAS is a non-destructive testing approach that allows the subsequent study of a sample by other methods. As experimental equipment for many applications, PAS is commercially produced and is relatively cheap, thus, increasingly more research laboratories are using PAS for basic research, diagnostics of machine parts working in hard conditions, and for characterization of high-tech materials. -
![The PLUTO Experiment at DORIS (DESY) and the Discovery of the Gluon (A Recollection]](https://docslib.b-cdn.net/cover/8568/the-pluto-experiment-at-doris-desy-and-the-discovery-of-the-gluon-a-recollection-478568.webp)
The PLUTO Experiment at DORIS (DESY) and the Discovery of the Gluon (A Recollection]
(9.46 GeV) and the gluon discovery (a critical recollection of PLUTO results)* Bruno R. Stella1,a and Hans-Jürgen Meyer2,b 1 Department of Physics of Roma Tre University and INFN; Rome, Italy 2 formerly at Department of Physics, Siegen University; Siegen, Germany Abstract. The hadronic decays of (9.46 GeV) were first studied by the PLUTO experiment at the DORIS e+e- storage ring (DESY). With the aim of determining the contribution of PLUTO to the discovery of the gluon, as members of this former collaboration we have reconsidered all the scientific material produced by PLUTO in 1978 and the first half of 1979. It results clearly that the experiment demonstrated the main decay of the (9.46 GeV) resonance to be mediated by 3 gluons, by providing evidence for the agreement of this hypothesis with average values and differential distributions of all possible experimental variables and by excluding all other possible alternative models. Jettiness resulted evident by the average transverse momentum <pT> with respect to the event thrust axis, which was the same as experimentally observed by PLUTO itself at nearby continuum c.m.s. energies for 2-quark jet events. On the contrary, the average sphericity <S> and more topological variables as well as the momentum distribution showed a net difference with the same data comparison, a result compatible with jettiness only in case of more than 2 jets. Flatness as consequence of a 3-body decay (therefore 3 jets) was indicated by the low average momentum out of the event plane <pout>, altogether a result being independent of models. -
Electron - Positron Annihilation
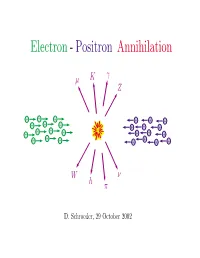
Electron - Positron Annihilation γ µ K Z − − − + + + − − − + + + − − − − + + + − − − + + + + W ν h π D. Schroeder, 29 October 2002 OUTLINE • Electron-positron storage rings • Detectors • Reaction examples e+e− −→ e+e− [Inventory of known particles] e+e− −→ µ+µ− e+e− −→ q q¯ e+e− −→ W +W − • The future:Linear colliders Electron-Positron Colliders Hamburg Novosibirsk 11 GeV 12 GeV 47 GeV Geneva 200 GeV Ithaca Tokyo Stanford 12 GeV 64 GeV 8 GeV 12 GeV 30 GeV 100 GeV Beijing 12 GeV 4 GeV Size (R) and Cost ($) of an e+e− Storage Ring βE4 $=αR + ( E = beam energy) R d $ βE4 Find minimum $: 0= = α − dR R2 β =⇒ R = E2, $=2 αβ E2 α SPEAR: E = 8 GeV, R = 40 m, $ = 5 million LEP: E = 200 GeV, R = 4.3 km, $ = 1 billion + − + − Example 1: e e −→ e e e− total momentum = 0 θ − total energy = 2E e e+ Probability(E,θ)=? e+ E-dependence follows from dimensional analysis: density = ρ− A density = ρ+ − + × 2 Probability = (ρ− ρ+ − + A) (something with units of length ) ¯h ¯hc When E m , the only relevant length is = e p E 1 =⇒ Probability ∝ E2 at SPEAR Augustin, et al., PRL 34, 233 (1975) 6000 5000 4000 Ecm = 4.8 GeV 3000 2000 Number of Counts 1000 Theory 0 −0.8 −0.40 0.40.8 cos θ Prediction for e+e− −→ e+e− event rate (H. J. Bhabha, 1935): event dσ e4 1 + cos4 θ 2 cos4 θ 1 + cos2 θ ∝ = 2 − 2 + rate dΩ 32π2E2 4 θ 2 θ 2 cm sin 2 sin 2 Interpretation of Bhabha’sformula (R. -

Jet Production and High Pt Phenomena in Photon-Photon Reactions*
JET PRODUCTION AND HIGH PT PHENOMENA IN PHOTON-PHOTON REACTIONS* NORBERT WERMES ~" Stanford Linear Accelerator Center Stanford University, Stanford, California 94305 ABSTRACT The status of experimental investigations of high PT phenomena and jet production in photon- photon collisions is reviewed. Taking the challenging questions on hard scattering processes in ~/ff reactions as a guide, the experimental approach to these questions is summarized. Results from the PETRA experiments CELLO, JADE, PLUTO, and TASSO are presented including preliminary results on the Q2-dependence of jet cross sections. Experimental limitations and background problems are discussed. Zusammenfassung -- Es wird ein Uberblick fiber den Stand experimenteller Untersuchungen yon high-PT Ph~nomenen und der Erzeugung von Jets in Photon-Photon Wechselwirkungen gegeben. Anhand der herausfordernden Fragen beziiglich harter Streuprozesse in ~/ff Reaktionen wird der experimentelle Ansatz zur Beantwortung dieser Fragen zusammengefasst. Ergebnisse der PETRA Experimente CELLO, JADE, PLUTO und TASSO werden presentiert. Vorli~ufige Untersuchungen der Q2-Abh~ngigkeit von Jet-Wirkungsquerschnitten sowie experimentelle Einschr~nkungen und Untergrundprobleme werden diskutiert. * Work supported by the Department of Energy, contract DE-AC03-76SF00515. ? Alexander yon Humboldt Fellow. 120 1. INTRODUCTION This talk reviews experimental results on hard scattering reactions in qff collisions via high PT phenomena. The talk is divided into three parts. First I shall try to list the physics challenges for photon- photon experiments, in the context of hard scattering processes at high PT. In the main part the experimental approach to these challenging questions is discussed. It will be explained why we believe that hard scattering processes do exist. Then the explicit jet-searches performed by the different experiments are reviewed. -

QCD at Colliders
Particle Physics Dr Victoria Martin, Spring Semester 2012 Lecture 10: QCD at Colliders !Renormalisation in QCD !Asymptotic Freedom and Confinement in QCD !Lepton and Hadron Colliders !R = (e+e!!hadrons)/(e+e!"µ+µ!) !Measuring Jets !Fragmentation 1 From Last Lecture: QCD Summary • QCD: Quantum Chromodymanics is the quantum description of the strong force. • Gluons are the propagators of the QCD and carry colour and anti-colour, described by 8 Gell-Mann matrices, !. • For M calculate the appropriate colour factor from the ! matrices. 2 2 • The coupling constant #S is large at small q (confinement) and large at high q (asymptotic freedom). • Mesons and baryons are held together by QCD. • In high energy collisions, jets are the signatures of quark and gluon production. 2 Gluon self-Interactions and Confinement , Gluon self-interactions are believed to give e+ q rise to colour confinement , Qualitative picture: •Compare QED with QCD •In QCD “gluon self-interactions squeeze lines of force into Gluona flux tube self-Interactions” ande- Confinementq , + , What happens whenGluon try self-interactions to separate two are believedcoloured to giveobjects e.g. qqe q rise to colour confinement , Qualitativeq picture: q •Compare QED with QCD •In QCD “gluon self-interactions squeeze lines of force into a flux tube” e- q •Form a flux tube, What of happensinteracting when gluons try to separate of approximately two coloured constant objects e.g. qq energy density q q •Require infinite energy to separate coloured objects to infinity •Form a flux tube of interacting gluons of approximately constant •Coloured quarks and gluons are always confined within colourless states energy density •In this way QCD provides a plausible explanation of confinement – but not yet proven (although there has been recent progress with Lattice QCD) Prof. -

Probing 23% of the Universe at the Large Hadron Collider
Probing 23% of the Universe at the Large Hadron Collider Will Flanagan1 Advisor: Dr Teruki Kamon2 In close collaboration with Bhaskar Dutta2, Alfredo Gurrola2, Nikolay Kolev3, Tom Crockett2, Michael VanDyke2, and Abram Krislock2 1University of Colorado at Boulder, Cyclotron REU Program 2Texas A&M University 3University of Regina Introduction What is cosmologically significant about ‘focus Analysis With recent astronomical measurements, point’? We first decide which events we want to look for. χ~0 ~0 we know that 23% of the Universe is The 1is allowed to annihilate with itself since it is Since χ 1 is undetectable (otherwise it wouldn’t be ‘dark composed of dark matter, whose origin is its own antimatter particle. The χ~ 0 -χ~0 annihilation matter’!), we look for events with a 1 1 Red – Jet distribution unknown. Supersymmetry (SUSY), a leading cross section is typically too small (predicting a relic after MET cut large amount of missing transverse theory in particle physics, provides us with a cold dark χ~0 Z channel dark matter density that is too energy. Also, due to the nature of 1 u- matter candidate, the lightest supersymmetric particle Z0 large). The small µ of focus these decays (shown below) we also χ~0 (LSP). SUSY particles, including the LSP, can be 1 u point x require two energetic jets. 2 f 1 Ω ~0 ~h dx created at the Large Hadron Collider (LHC) at CERN. allows for a larger annihilation χ1 ∫ 0 σ v { ann g~ 2 energetic jets + 2 leptons We perform a systematic study to characterize the cross section for our dark 0.23 698 u- + MET 2 g~ SUSY signals in the "focus point" region, one of a few matter candidate by opening πα ~ u - σ annv = 2 u l cosmologically-allowed parameter regions in our SUSY up the ‘Z channel’ (pictured 321 8M χ~0 l+ 0.9 pb 2 ~+ model. -

Sensitivity Physics. D KAONS, Or
A PERIODICAL OF PARTICLE PHYSICS WINTER 1995 VOL. 25, NUMBER 4 Editors RENE DONALDSON, BILL KIRK Contributing Editor MICHAEL RIORDAN Editorial Advisory Board JAMES BJORKEN, GEORGE BROWN, ROBERT N. CAHN, DAVID HITLIN, JOEL PRIMACK, NATALIE ROE, ROBERT SIEMANN Illustrations page 4 TERRY ANDERSON Distribution CRYSTAL TILGHMAN The Beam Line is published quarterly by the Stanford Linear Accelerator Center, PO Box 4349, Stanford, CA 94309. Telephone: (415) 926-2585 INTERNET: [email protected] FAX: (415) 926-4500 Issues of the Beam Line are accessible electronically on uayc ou the World Wide Web at http://www.slac.stanford.edu/ pubs/beamline/beamline.html SLAC is operated by Stanford University under contract with the U.S. Department of Energy. The opinions of the authors do not necessarily reflect the policy of the Stanford Linear Accelerator Center. Cover: Martin Perl (left) and Frederick Reines (center) receive the 1995 Nobel Prize in physics from His Majesty the King of Sweden at the awards ceremony last December. (Photograph courtesy of Joseph Peri) Printed on recycled paper tj) . CONTENTS FEATURES "We conclude that the signature e-/. events cannot be explained either by the production and decay of any presently known particles 4 Discovery of the Tau or as coming from any of the well- THE ROLE OF MOTIVATION & understood interactions which can TECHNOLOGY IN EXPERIMENTAL conventionally lead to an e and a PARTICLE PHYSICS gu in the final state. A possible ex- One of this year's Nobel Prize in physics planation for these events is the recipients describes the discovery production and decay of a pair of of the tau lepton in his 1975 new particles, each having a mass SLAC experiment. -

E+ E~ ANNIHILATION Hinrich Meyer, Fachbereich Physik, Universitдt
- 155 - e+e~ ANNIHILATION Hinrich Meyer, Fachbereich Physik, Universität Wuppertal, Fed. Rep. Germany CONTENT INTRODUCTION 1. e+e~ STORAGE RINGS .1 Energy and Size .2 Luminosity .3 Energy range of one Ring .4 Energie resolution .5 Polarization 2. EXPERIMENTAL PROCEDURES .1 Storage Ring Detectors .2 Background .3 Luminosity Measurement .4 Radiative Corrections 3. QED-REACTIONS + . 1 e+e~ T T~ .2 e+e"+y+y~ . 3 e+e~ -»• e+e~ . 4 e+e_ •+y y 4. HADRON PRODUCTION IN e+e~ANNTHILATION .1 Total Cross Section .2 Average Event Properties .3 Two Jet Structure .4 Three Jet Structure .5 Gluon Properties - 156 - 5. SEARCH FOR NEW PARTICLES .1 Experimental Methods .2 Search for the sixth Flavor (t) .3 Properties of Q Q Resonances .4 New Leptons 6. YY ~ REACTIONS .1 General Properties .2 Resonance Production .3 £ for e,Y Scattering .4 Hard Scattering Processes .5 Photon Structure Function INTRODUCTION e+e storage rings have been proven to be an extremely fruitful techno• logical invention for particle physics. They were originally designed to provide stringent experimental tests of the theory of leptons and photons QED (Quantum-Electro-Dynamics). QED has passed these tests beautifully up to the highest energies (PETRA) so far achieved. The great successes of the e+e storage rings however are in the field of strong interaction physics. The list below gives a very brief overview of the historical development by quoting the highlights of physics results from e+e storage rings with the completion of storage rings of higher and higher energy (see Fig.1). YEAR -

Model of N¯ Annihilation in Experimental Searches for N¯ Transformations
PHYSICAL REVIEW D 99, 035002 (2019) Model of n¯ annihilation in experimental searches for n¯ transformations E. S. Golubeva,1 J. L. Barrow,2 and C. G. Ladd2 1Institute for Nuclear Research, Russian Academy of Sciences, Prospekt 60-letiya Oktyabrya 7a, Moscow, 117312, Russia 2University of Tennessee, Department of Physics, 401 Nielsen Physics Building, 1408 Circle Drive, Knoxville, Tennessee 37996, USA (Received 24 July 2018; published 5 February 2019) Searches for baryon number violation, including searches for proton decay and neutron-antineutron transformation (n → n¯), are expected to play an important role in the evolution of our understanding of beyond standard model physics. The n → n¯ is a key prediction of certain popular theories of baryogenesis, and experiments such as the Deep Underground Neutrino Experiment and the European Spallation Source plan to search for this process with bound- and free-neutron systems. Accurate simulation of this process in Monte Carlo will be important for the proper reconstruction and separation of these rare events from background. This article presents developments towards accurate simulation of the annihilation process for 12 use in a cold, free neutron beam for n → n¯ searches from nC¯ annihilation, as 6 C is the target of choice for the European Spallation Source’s NNBar Collaboration. Initial efforts are also made in this paper to 40 perform analogous studies for intranuclear transformation searches in 18Ar nuclei. DOI: 10.1103/PhysRevD.99.035002 I. INTRODUCTION evacuated, magnetically shielded pipe of 76 m in length (corresponding to a flight time of ∼0.1 s), until being A. Background 12 allowed to hit a target of carbon (6 C) foil (with a thickness As early as 1967, A. -

Quark Annihilation and Lepton Formation Versus Pair Production and Neutrino Oscillation: the Fourth Generation of Leptons
Volume 2 PROGRESS IN PHYSICS April, 2011 Quark Annihilation and Lepton Formation versus Pair Production and Neutrino Oscillation: The Fourth Generation of Leptons T. X. Zhang Department of Physics, Alabama A & M University, Normal, Alabama E-mail: [email protected] The emergence or formation of leptons from particles composed of quarks is still re- mained very poorly understood. In this paper, we propose that leptons are formed by quark-antiquark annihilations. There are two types of quark-antiquark annihilations. Type-I quark-antiquark annihilation annihilates only color charges, which is an incom- plete annihilation and forms structureless and colorless but electrically charged leptons such as electron, muon, and tau particles. Type-II quark-antiquark annihilation an- nihilates both electric and color charges, which is a complete annihilation and forms structureless, colorless, and electrically neutral leptons such as electron, muon, and tau neutrinos. Analyzing these two types of annihilations between up and down quarks and antiquarks with an excited quantum state for each of them, we predict the fourth gener- ation of leptons named lambda particle and neutrino. On the contrary quark-antiquark annihilation, a lepton particle or neutrino, when it collides, can be disintegrated into a quark-antiquark pair. The disintegrated quark-antiquark pair, if it is excited and/or changed in flavor during the collision, will annihilate into another type of lepton par- ticle or neutrino. This quark-antiquark annihilation and pair production scenario pro- vides unique understanding for the formation of leptons, predicts the fourth generation of leptons, and explains the oscillation of neutrinos without hurting the standard model of particle physics. -

GLAST Science Glossary (PDF)
GLAST SCIENCE GLOSSARY Source: http://glast.sonoma.edu/science/gru/glossary.html Accretion — The process whereby a compact object such as a black hole or neutron star captures matter from a normal star or diffuse cloud. Active galactic nuclei (AGN) — The central region of some galaxies that appears as an extremely luminous point-like source of radiation. They are powered by supermassive black holes accreting nearby matter. Annihilation — The process whereby a particle and its antimatter counterpart interact, converting their mass into energy according to Einstein’s famous formula E = mc2. For example, the annihilation of an electron and positron results in the emission of two gamma-ray photons, each with an energy of 511 keV. Anticoincidence Detector — A system on a gamma-ray observatory that triggers when it detects an incoming charged particle (cosmic ray) so that the telescope will not mistake it for a gamma ray. Antimatter — A form of matter identical to atomic matter, but with the opposite electric charge. Arcminute — One-sixtieth of a degree on the sky. Like latitude and longitude on Earth's surface, we measure positions on the sky in angles. A semicircle that extends up across the sky from the eastern horizon to the western horizon is 180 degrees. One degree, therefore, is not a very big angle. An arcminute is an even smaller angle, 1/60 as large as a degree. The Moon and Sun are each about half a degree across, or about 30 arcminutes. If you take a sharp pencil and hold it at arm's length, then the point of that pencil as seen from your eye is about 3 arcminutes across. -

Electrical Engineering Dictionary
ratio of the power per unit solid angle scat- tered in a specific direction of the power unit area in a plane wave incident on the scatterer R from a specified direction. RADHAZ radiation hazards to personnel as defined in ANSI/C95.1-1991 IEEE Stan- RS commonly used symbol for source dard Safety Levels with Respect to Human impedance. Exposure to Radio Frequency Electromag- netic Fields, 3 kHz to 300 GHz. RT commonly used symbol for transfor- mation ratio. radial basis function network a fully R-ALOHA See reservation ALOHA. connected feedforward network with a sin- gle hidden layer of neurons each of which RL Typical symbol for load resistance. computes a nonlinear decreasing function of the distance between its received input and Rabi frequency the characteristic cou- a “center point.” This function is generally pling strength between a near-resonant elec- bell-shaped and has a different center point tromagnetic field and two states of a quan- for each neuron. The center points and the tum mechanical system. For example, the widths of the bell shapes are learned from Rabi frequency of an electric dipole allowed training data. The input weights usually have transition is equal to µE/hbar, where µ is the fixed values and may be prescribed on the electric dipole moment and E is the maxi- basis of prior knowledge. The outputs have mum electric field amplitude. In a strongly linear characteristics, and their weights are driven 2-level system, the Rabi frequency is computed during training. equal to the rate at which population oscil- lates between the ground and excited states.