M. S. Molodensky in Memoriam
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Results in I and II Cycles of the Internet Music Competition 2014
Results in I and II cycles of the Internet Music Competition 2014 I cycle: Duo, chamber ensemble, piano ensemble, choir, orchestra, percussion II cycle: Piano, bassoon, flute, french horn, clarinet, oboe, saxophone, trombone, trumpet, tube Internet Music Competition which passes completely through the Internet and it is unique event since its inception. In first and second cycles of the contest in 2014, was attended by 914 contestants from 22 countries and 198 cities from 272 schools: I cycle: "Duo" – 56 contestants "Piano Ensemble" – 94 contestants "Chamber Ensemble" – 73 contestants "Choir" – 23 contestants "Orchestra" – 28 contestant "Percussion "– 13 contestants. II cycle: "Piano" – 469 contestants "Bassoon" – 7 contestants "Flute" – 82 contestants "French horn" – 3 contestants "Clarinet" – 17 contestants "Oboe" – 8 contestants "Saxophone" – 27 contestants "Trombone" – 2 contestants "Trumpet" – 9 contestants "Tube" – 3 contestants The jury was attended by 37 musicians from 13 countries, many of whom are eminent teachers, musicians and artists who teach at prestigious music institutions are soloists and play in the top 10 best orchestras and opera houses. The winners of the first cycle in Masters Final Internet Music Competition 2014: "Duo" – Djamshid Saidkarimov, Pak Artyom (Tashkent, Uzbekistan) "Piano Ensemble" – Koval Ilya, Koval Yelissey (Karaganda, Kazakhstan) "Chamber Ensemble" – Creative Quintet (Sanok, Poland) "Choir" – Womens Choir Ave musiсa HGEU (Odessa, Ukraine) "Orchestra" – “Victoria” (Samara, Russia) "Percussion" – -
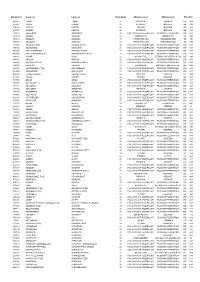
FÁK Állomáskódok
Állomáskód Orosz név Latin név Vasút kódja Államnév orosz Államnév latin Államkód 406513 1 МАЯ 1 MAIA 22 УКРАИНА UKRAINE UA 804 085827 ААКРЕ AAKRE 26 ЭСТОНИЯ ESTONIA EE 233 574066 ААПСТА AAPSTA 28 ГРУЗИЯ GEORGIA GE 268 085780 ААРДЛА AARDLA 26 ЭСТОНИЯ ESTONIA EE 233 269116 АБАБКОВО ABABKOVO 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 737139 АБАДАН ABADAN 29 УЗБЕКИСТАН UZBEKISTAN UZ 860 753112 АБАДАН-I ABADAN-I 67 ТУРКМЕНИСТАН TURKMENISTAN TM 795 753108 АБАДАН-II ABADAN-II 67 ТУРКМЕНИСТАН TURKMENISTAN TM 795 535004 АБАДЗЕХСКАЯ ABADZEHSKAIA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 795736 АБАЕВСКИЙ ABAEVSKII 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 864300 АБАГУР-ЛЕСНОЙ ABAGUR-LESNOI 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 865065 АБАГУРОВСКИЙ (РЗД) ABAGUROVSKII (RZD) 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 699767 АБАИЛ ABAIL 27 КАЗАХСТАН REPUBLIC OF KAZAKHSTAN KZ 398 888004 АБАКАН ABAKAN 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 888108 АБАКАН (ПЕРЕВ.) ABAKAN (PEREV.) 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 398904 АБАКЛИЯ ABAKLIIA 23 МОЛДАВИЯ MOLDOVA, REPUBLIC OF MD 498 889401 АБАКУМОВКА (РЗД) ABAKUMOVKA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 882309 АБАЛАКОВО ABALAKOVO 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 408006 АБАМЕЛИКОВО ABAMELIKOVO 22 УКРАИНА UKRAINE UA 804 571706 АБАША ABASHA 28 ГРУЗИЯ GEORGIA GE 268 887500 АБАЗА ABAZA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 887406 АБАЗА (ЭКСП.) ABAZA (EKSP.) 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 -

TULA М4 Rail М2 М2
CATALOGUE OF INDUSTRIAL PRODUCTS EXPORTED BY THE TULA REGION 1 CATALOGUE CONTENTS INFORMATION 3 MECHANICAL ENGINEERING 6 METALLURGICAL INDUSTRY 16 CHEMICAL INDUSTRY 25 LIGHT INDUSTRY 36 FOOD INDUSTRY 48 CONTACT INFORMATION 62 2 CATALOGUE CONTENTS “THE FOREIGN TRADE TURNOVER STRUCTURE NOW MEETS ALL THE CRITERIA FOR ECONOMIC DEVELOPMENT AND IS EXPORT-ORIENTED. WE NEED TO INCREASE THE VOLUME OF EXPORTS AND FIND NEW SALES MARKETS.” Governor of the Tula Region Alexei Dyumin 3 TULA REGION TRADE WITH MAJOR TRADING PARTNERS: 126 USA, CHINA, COUNTRIES BELARUS, ALGERIA, TURKEY, UAE, GERMANY 36,2% Chemical industry products and rubber 28,1% Other goods 6,8% Mechanical engineering products 5% Foods and raw materials Population Total area Tula Novomoskovsk 23,9% Metals and metal 1 466 127 25 700 550,8 125,2 products people sq. km thousand people thousand people EXPORT STRUCTURE EXPORT 4 TULA REGION MOSCOW М2 MOSCOW REGION TWO FEDERAL HIGHWAYS • M2 ‘Crimea’ М4 Zaokskiy Rail • M4 ‘Don’ KALUGA REGION Aleksin RAILWAY ROUTES Yasnogorsk • MOSCOW–KHARKOV–SIMFEROPOL, Venoyv • MOSCOW–DONBAS; TULA TRANSPORT ROUTES Dubna Suvorov Novomoskovsk RYAZAN REGION • Tula – M4 ‘Don’ Transcaucasia, Western Asia (part of the Chekalin Shchyokino Uzlovaya Kimovsk European route E 115) Odoyev Kireyevsk • Tula – M2 ‘Crimea’ Europe (part of the European route E105) Belyov Arsenyevo Bogoroditsk Plavsk Tyoploye Volovo AIR TRAFFIC: • Sheremetyevo (210 km) – more than 230 domestic and М2 Chern Kurkino international destinations • Domodedovo (170 km) – 194 destinations Arkhangelskoye LIPETSK • Vnukovo (180 km) – more than 200,000 domestic and REGION international destinations ORYOL REGION Yefremov • Kaluga Airport (110 km) – 9 domestic destinations М4 5 MECHANICAL ENGINEERING THE TULAMASHZAVOD PRODUCTION ASSOCIATION The TULAMASHZAVOD Production Association is a major holding that includes the parent TULAMASHZAVOD Joint-Stock Company and twenty subsidiaries that focus equally on both the manufacturing of products for the defence industry and civilian products. -

ANNEX J Exposures and Effects of the Chernobyl Accident
ANNEX J Exposures and effects of the Chernobyl accident CONTENTS Page INTRODUCTION.................................................. 453 I. PHYSICALCONSEQUENCESOFTHEACCIDENT................... 454 A. THEACCIDENT........................................... 454 B. RELEASEOFRADIONUCLIDES ............................. 456 1. Estimation of radionuclide amounts released .................. 456 2. Physical and chemical properties of the radioactivematerialsreleased ............................. 457 C. GROUNDCONTAMINATION................................ 458 1. AreasoftheformerSovietUnion........................... 458 2. Remainderofnorthernandsouthernhemisphere............... 465 D. ENVIRONMENTAL BEHAVIOUR OF DEPOSITEDRADIONUCLIDES .............................. 465 1. Terrestrialenvironment.................................. 465 2. Aquaticenvironment.................................... 466 E. SUMMARY............................................... 466 II. RADIATIONDOSESTOEXPOSEDPOPULATIONGROUPS ........... 467 A. WORKERS INVOLVED IN THE ACCIDENT .................... 468 1. Emergencyworkers..................................... 468 2. Recoveryoperationworkers............................... 469 B. EVACUATEDPERSONS.................................... 472 1. Dosesfromexternalexposure ............................. 473 2. Dosesfrominternalexposure.............................. 474 3. Residualandavertedcollectivedoses........................ 474 C. INHABITANTS OF CONTAMINATED AREAS OFTHEFORMERSOVIETUNION............................ 475 1. Dosesfromexternalexposure -

BR IFIC N° 2639 Index/Indice
BR IFIC N° 2639 Index/Indice International Frequency Information Circular (Terrestrial Services) ITU - Radiocommunication Bureau Circular Internacional de Información sobre Frecuencias (Servicios Terrenales) UIT - Oficina de Radiocomunicaciones Circulaire Internationale d'Information sur les Fréquences (Services de Terre) UIT - Bureau des Radiocommunications Part 1 / Partie 1 / Parte 1 Date/Fecha 10.03.2009 Description of Columns Description des colonnes Descripción de columnas No. Sequential number Numéro séquenciel Número sequencial BR Id. BR identification number Numéro d'identification du BR Número de identificación de la BR Adm Notifying Administration Administration notificatrice Administración notificante 1A [MHz] Assigned frequency [MHz] Fréquence assignée [MHz] Frecuencia asignada [MHz] Name of the location of Nom de l'emplacement de Nombre del emplazamiento de 4A/5A transmitting / receiving station la station d'émission / réception estación transmisora / receptora 4B/5B Geographical area Zone géographique Zona geográfica 4C/5C Geographical coordinates Coordonnées géographiques Coordenadas geográficas 6A Class of station Classe de station Clase de estación Purpose of the notification: Objet de la notification: Propósito de la notificación: Intent ADD-addition MOD-modify ADD-ajouter MOD-modifier ADD-añadir MOD-modificar SUP-suppress W/D-withdraw SUP-supprimer W/D-retirer SUP-suprimir W/D-retirar No. BR Id Adm 1A [MHz] 4A/5A 4B/5B 4C/5C 6A Part Intent 1 109013920 ARG 7156.0000 CASEROS ARG 58W28'29'' 32S27'41'' FX 1 ADD 2 109013877 -

BR IFIC N° 2646 Index/Indice
BR IFIC N° 2646 Index/Indice International Frequency Information Circular (Terrestrial Services) ITU - Radiocommunication Bureau Circular Internacional de Información sobre Frecuencias (Servicios Terrenales) UIT - Oficina de Radiocomunicaciones Circulaire Internationale d'Information sur les Fréquences (Services de Terre) UIT - Bureau des Radiocommunications Part 1 / Partie 1 / Parte 1 Date/Fecha 16.06.2009 Description of Columns Description des colonnes Descripción de columnas No. Sequential number Numéro séquenciel Número sequencial BR Id. BR identification number Numéro d'identification du BR Número de identificación de la BR Adm Notifying Administration Administration notificatrice Administración notificante 1A [MHz] Assigned frequency [MHz] Fréquence assignée [MHz] Frecuencia asignada [MHz] Name of the location of Nom de l'emplacement de Nombre del emplazamiento de 4A/5A transmitting / receiving station la station d'émission / réception estación transmisora / receptora 4B/5B Geographical area Zone géographique Zona geográfica 4C/5C Geographical coordinates Coordonnées géographiques Coordenadas geográficas 6A Class of station Classe de station Clase de estación Purpose of the notification: Objet de la notification: Propósito de la notificación: Intent ADD-addition MOD-modify ADD-ajouter MOD-modifier ADD-añadir MOD-modificar SUP-suppress W/D-withdraw SUP-supprimer W/D-retirer SUP-suprimir W/D-retirar No. BR Id Adm 1A [MHz] 4A/5A 4B/5B 4C/5C 6A Part Intent 1 109039087 AUT 17727.5000 250105A 199903A AUT 15E18'44'' 48N14'24'' FX 1 ADD -

TULA REGION TULA Moscow Moscow REGION Region
TULA REGION TULA Moscow Moscow REGION region Kaluga region Tula Novomoskovsk Ryazan region Lipetsk Oryol region region Population Total area Tula Novomoskovsk 1.5million 25 700km2 550 800 125 200 OVERVIEW OF TULA REGION ECONOMY GRP Manufacturing at comparable prices 40,5% (rating 2017) 578 bn rubles industries 103,4% Wholesale and retail trade 12,2% Industry in the region Industrial production growth 105,6 Transport and at comparable prices % communications 6,5% (2017) Agricultural output Real estate transactions 11,4% production growth at current prices 109,3% (2017) Agriculture 7,0% Investment at current prices (2017) 127,1 bn rubles Other kinds of economic 22,4% activities 9,4% at comparable prices to the same period in 2016 FORMULA FOR SUCCESS Favorable Tailor-made Tax logistics approach benefits Highly qualified workforce Good governance FAVORABLE LOGISTICS Nearest airports: Domodedovo - 2hours km 180 Vnukovo - 2hours from Moscow Kaluga - 1hour and 40minutes In direct proximity to the largest target market М2 Crimea M4 Don Moscow Railway: southern branch of the Paveletsky route Major national highways INVESTOR INDIVIDUAL ACCOMPONIMENT Support in establishing local production Location matching Legal support State support at both the federal Selection of contractors and regional levels Regional integrated development projects Consulting support Establishment and development of industrial parks PPP projects One-stop shop 24/7 TAX BENEFITS Property tax reduction 0% up to 4 tax periods Income tax reduction 15,5% up to 4 tax periods Projects from 50m rubles According to Tula region law No. 1390-ATR dated 06.02.2010 Investments in construction of infrastructure facilities According to Government Decrees of the Tula region No. -
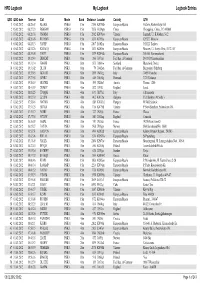
HRD Logbook Logbook Entries My Logbook
HRD Logbook My Logbook Logbook Entries QSO QSO date Time on Call Mode Band Distance Locator Country QTH 105.02.2012 08:28:07 RL6MA PSK63 15m 2150KN98xb European Russia Gukovo, Rostovskaya Obl 205.02.2012 08:27:23 BG8GAM PSK63 15m 7878OL39gm China Chongqing , China , P.C.400060 305.02.2012 08:26:38 US0MM PSK63 15m 2082KN98po Ukraine Lugansk, Ul. K.Marksa, 5-12 405.02.2012 08:26:03 RV3AMV PSK63 15m 1833KO85tu European Russia 129327, Moscow 505.02.2012 08:25:13 UA3RF PSK63 15m 2107LO02rq European Russia 392022, Tambov 605.02.2012 08:24:26 RX3AGQ PSK63 15m 1833KO85ts European Russia Moscow, Ul. Novyi Arbat, 31/12-107 705.02.2012 08:24:00 UA3PI PSK63 15m 1879KO94da European Russia 301650, Novomoskovsk 803.02.2012 19:32:43 DK0KAT PSK31 80m 260JO71ao Fed. Rep. of Germany D-01983 Grossraeschen 903.02.2012 19:31:14 GM4RS PSK31 80m 873IO80vw Scotland Blandford, Dorset 1003.02.2012 19:31:02 DL1OI PSK31 80m 79JO42wn Fed. Rep. of Germany Burgwedel / Fuhrberg 1103.02.2012 19:28:45 IK7GOD PSK31 80m 1269JN81eg Italy 70059 Trani Ba 1203.02.2012 19:27:58 OZ5RZ PSK31 80m 445JO65fq Denmark 2720 Vanloese 1303.02.2012 19:26:49 OE1TRB PSK31 80m 595JN88ef Austria Vienna, 1200 1403.02.2012 18:41:39 2E0WJC PSK63 40m 822IO93ft England Leeds 1503.02.2012 18:18:25 IT9QQM PSK31 40m 1631JM77al Italy Caltanissetta 1603.02.2012 18:12:30 LZ1XM PSK31 40m 1402KN12nr Bulgaria 1320 Bankya (Nr Sofia ) 1703.02.2012 17:58:46 HA7MG PSK31 40m 889KN07cd Hungary H-5008 Szolnok 1803.02.2012 17:51:25 UR7HA PSK31 40m 1710KN79di Ukraine P. -

Municipal Governance in Modern Russia
THE 45TH CONGRESS OF THE EUROPEAN REGIONAL SCIENCE ASSOCIATION 23-27 AUGUST, 2005, AMSTERDAM, THE NETHERLANDS German Vetrov ([email protected]) , Ioulia Zaitseva ([email protected]) , The Institute for Urban Economics, Moscow, Russian Federation MUNICIPAL GOVERNANCE IN MODERN RUSSIA Abstract The results of survey, Municipal Governance in Modern Russia, was conducted in 2003 – 2004 by the Institute for Urban Economics (IUE), are presented in the paper. The primary goal of the research is to take an inventory of the experience accumulated by the cities in the field of managing local development, focusing on such important parameters as local leaders’ awareness of new management technologies and popularity of such technologies, activity of municipalities at inter-municipal level, technical equipment of administrations. The study of the present status of municipal governance in Russia is all the more important now, with the beginning of a critically new period in the development of Russian cities. Internal and external factors of various nature determine the beginning of this period. On the one hand, relative economic stability in the country and experience accumulated over the years enabled many cities to turn at last from current problems and institutional reforms to strategic planning of their development. On the other hand, the system of local self-governance itself is being transformed drastically by the state – both in terms of territorial organization and municipal powers and interaction between different levels of government. Further transformation is determined by the new version of the Federal Law, On the General Principles of the Organization of Local Self-Governance in the Russian Federation, passed on October 6, 2003 (#131-FZ). -

TULA REGION TULA Moscow Moscow REGION Region
TULA REGION TULA Moscow Moscow REGION region Kaluga region Tula Novomoskovsk Ryazan region Lipetsk Oryol region region Population Total area Tula Novomoskovsk 1.5million 25 700km2 550 800 125 200 OVERVIEW OF TULA REGION ECONOMY GRP Manufacturing (rating 2017) 40,5% 562 bn rubles industries 104,4% Wholesale and retail trade 12,2% Industrial production GRP structure growth 106,2% Transport and (2017) communications 6,5% Agricultural output Real estate transactions 11,4% production growth 110,4% (2017) Agriculture 7,0% Investment at current prices (2017) 127 bn rubles Other kinds of economic 22,4% activities 109,4% at comparable prices to 2016 FORMULA FOR SUCCESS Favorable Tailor-made Tax logistics approach benefits Highly qualified workforce Good governance FAVORABLE LOGISTICS Nearest airports: Domodedovo - 2hours km 180 Vnukovo - 2hours from Moscow Kaluga - 1hour and 40minutes In direct proximity to the largest target market М2 Crimea M4 Don Moscow Railway: southern branch of the Paveletsky route Major national highways INVESTOR INDIVIDUAL ACCOMPONIMENT Support in establishing local production Location matching Legal support State support at both the federal Selection of contractors and regional levels Regional integrated development projects Consulting support Establishment and development of industrial parks PPP projects One-stop shop 24/7 TAX BENEFITS Property tax reduction 0% up to 10 tax periods Income tax reduction 15,5% Projects from 100m rubles According to Tula region law No. 1390-ATR dated 06.02.2010 Investments in construction -
International Out-Of-Delivery-Area and Out-Of-Pickup-Area Surcharges
INTERNATIONAL OUT-OF-DELIVERY-AREA AND OUT-OF-PICKUP-AREA SURCHARGES International shipments (subject to service availability) delivered to or picked up from remote and less-accessible locations are assessed an out-of-delivery area or out-of-pickup-area surcharge. Refer to local service guides for surcharge amounts. The following is a list of postal codes and cities where these surcharges apply. Effective: January 17, 2011 Albania Crespo Pinamar 0845-0847 3254 3612 4380-4385 Berat Daireaux Puan 0850 3260 3614 4387-4388 Durres Diamante Puerto Santa Cruz 0852-0854 3264-3274 3616-3618 4390 Elbasan Dolores Puerto Tirol 0860-0862 3276-3282 3620-3624 4400-4407 Fier Dorrego Quequen 0870 3284 3629-3630 4410-4413 Kavaje El Bolson Rawson 0872 3286-3287 3633-3641 4415-4428 Kruje El Durazno Reconquista 0880 3289 3644 4454-4455 Kucove El Trebol Retiro San Pablo 0885-0886 3292-3294 3646-3647 4461-4462 Lac Embalse Rincon De Los Sauces 0909 3300-3305 3649 4465 Lezha Emilio Lamarca Rio Ceballos 2312 3309-3312 3666 4467-4468 Lushnje Esquel Rio Grande 2327-2329 3314-3315 3669-3670 4470-4472 Shkodra Fair Rio Segundo 2331 3317-3319 3672-3673 4474-4475 Vlore Famailla Rio Tala 2333-2347 3323-3325 3675 4477-4482 Firmat Rojas 2350-2360 3351 3677-3678 4486-4494 Andorra* Florentino Ameghino Rosario De Lerma 2365 3360-3361 3682-3683 4496-4498 Andorra Franck Rufino 2369-2372 3371 3685 4568-4569 Andorra La Vella General Alvarado Russel 2379-2382 3373 3687-3688 4571 El Serrat General Belgrano Salina De Piedra 2385-2388 3375 3690-3691 4580-4581 Encamp General Galarza -

FÁK Állomáskódok
Állomáskód Orosz név Latin név Vasút kódja Államnév orosz Államnév latin Államkód 010002 ПЕТРОЗАВОДСК PETROZAVODSK 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010214 ГОЛИКОВКА GOLIKOVKA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010318 ШУЙСКИЙ МОСТ SHUISKII MOST 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010322 ТОМИЦЫ TOMICE 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010407 ШУЙСКАЯ SHUISKAIA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010411 ОСТ. ПУНКТ 427 КМ OST. PUNKT 427 KM 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010426 ЛУЧЕВОЙ LUCHEVOI 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010500 СУНА SUNA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010515 ОСТ. ПУНКТ 437 КМ OST. PUNKT 437 KM 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010604 ЗАДЕЛЬЕ (РЗД) ZADELE 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010708 КОНДОПОГА KONDOPOGA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010727 МЯНСЕЛЬГА MIANSELGA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010731 ИЛЕМСЕЛЬГА ILEMSELGA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010801 КЕДРОЗЕРО KEDROZERO 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010820 ЛИЖМА LIJMA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010835 НОВЫЙ ПОСЕЛОК NOVEI POSELOK 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010843 ВИКШЕЗЕРО VIKSHEZERO 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 010905 НИГОЗЕРО NIGOZERO 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION RU 643 011005 КЯППЕСЕЛЬГА KIAPPESELGA 20 РОССИЙСКАЯ ФЕДЕРАЦИЯ RUSSIAN FEDERATION