Differential Geometry in Physics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Toponogov.V.A.Differential.Geometry
Victor Andreevich Toponogov with the editorial assistance of Vladimir Y. Rovenski Differential Geometry of Curves and Surfaces A Concise Guide Birkhauser¨ Boston • Basel • Berlin Victor A. Toponogov (deceased) With the editorial assistance of: Department of Analysis and Geometry Vladimir Y. Rovenski Sobolev Institute of Mathematics Department of Mathematics Siberian Branch of the Russian Academy University of Haifa of Sciences Haifa, Israel Novosibirsk-90, 630090 Russia Cover design by Alex Gerasev. AMS Subject Classification: 53-01, 53Axx, 53A04, 53A05, 53A55, 53B20, 53B21, 53C20, 53C21 Library of Congress Control Number: 2005048111 ISBN-10 0-8176-4384-2 eISBN 0-8176-4402-4 ISBN-13 978-0-8176-4384-3 Printed on acid-free paper. c 2006 Birkhauser¨ Boston All rights reserved. This work may not be translated or copied in whole or in part without the writ- ten permission of the publisher (Birkhauser¨ Boston, c/o Springer Science+Business Media Inc., 233 Spring Street, New York, NY 10013, USA) and the author, except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and re- trieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. Printed in the United States of America. (TXQ/EB) 987654321 www.birkhauser.com Contents Preface ....................................................... vii About the Author ............................................. -

Kähler Manifolds, Ricci Curvature, and Hyperkähler Metrics
K¨ahlermanifolds, Ricci curvature, and hyperk¨ahler metrics Jeff A. Viaclovsky June 25-29, 2018 Contents 1 Lecture 1 3 1.1 The operators @ and @ ..........................4 1.2 Hermitian and K¨ahlermetrics . .5 2 Lecture 2 7 2.1 Complex tensor notation . .7 2.2 The musical isomorphisms . .8 2.3 Trace . 10 2.4 Determinant . 11 3 Lecture 3 11 3.1 Christoffel symbols of a K¨ahler metric . 11 3.2 Curvature of a Riemannian metric . 12 3.3 Curvature of a K¨ahlermetric . 14 3.4 The Ricci form . 15 4 Lecture 4 17 4.1 Line bundles and divisors . 17 4.2 Hermitian metrics on line bundles . 18 5 Lecture 5 21 5.1 Positivity of a line bundle . 21 5.2 The Laplacian on a K¨ahlermanifold . 22 5.3 Vanishing theorems . 25 6 Lecture 6 25 6.1 K¨ahlerclass and @@-Lemma . 25 6.2 Yau's Theorem . 27 6.3 The @ operator on holomorphic vector bundles . 29 1 7 Lecture 7 30 7.1 Holomorphic vector fields . 30 7.2 Serre duality . 32 8 Lecture 8 34 8.1 Kodaira vanishing theorem . 34 8.2 Complex projective space . 36 8.3 Line bundles on complex projective space . 37 8.4 Adjunction formula . 38 8.5 del Pezzo surfaces . 38 9 Lecture 9 40 9.1 Hirzebruch Signature Theorem . 40 9.2 Representations of U(2) . 42 9.3 Examples . 44 2 1 Lecture 1 We will assume a basic familiarity with complex manifolds, and only do a brief review today. Let M be a manifold of real dimension 2n, and an endomorphism J : TM ! TM satisfying J 2 = −Id. -

Quantum Dynamical Manifolds - 3A
Quantum Dynamical Manifolds - 3a. Cold Dark Matter and Clifford’s Geometrodynamics Conjecture D.F. Scofield ApplSci, Inc. 128 Country Flower Rd. Newark, DE, 19711 scofield.applsci.com (June 11, 2001) The purpose of this paper is to explore the concepts of gravitation, inertial mass and spacetime from the perspective of the geometrodynamics of “mass-spacetime” manifolds (MST). We show how to determine the curvature and torsion 2-forms of a MST from the quantum dynamics of its constituents. We begin by reformulating and proving a 1876 conjecture of W.K. Clifford concerning the nature of 4D MST and gravitation, independent of the standard formulations of general relativity theory (GRT). The proof depends only on certain derived identities involving the Riemann curvature 2-form in a 4D MST having torsion. This leads to a new metric-free vector-tensor fundamental law of dynamical gravitation, linear in pairs of field quantities which establishes a homeomorphism between the new theory of gravitation and electromagnetism based on the mean curvature potential. Its generalization leads to Yang-Mills equations. We then show the structure of the Riemann curvature of a 4D MST can be naturally interpreted in terms of mass densities and currents. By using the trace curvature invariant, we find a parity noninvariance is possible using a de Sitter imbedding of the Poincar´egroup. The new theory, however, is equivalent to the Newtonian one in the static, large scale limit. The theory is compared to GRT and shown to be compatible outside a gravitating mass in the absence of torsion. We apply these results on the quantum scale to determine the gravitational field of leptons. -

MAT 362 at Stony Brook, Spring 2011
MAT 362 Differential Geometry, Spring 2011 Instructors' contact information Course information Take-home exam Take-home final exam, due Thursday, May 19, at 2:15 PM. Please read the directions carefully. Handouts Overview of final projects pdf Notes on differentials of C1 maps pdf tex Notes on dual spaces and the spectral theorem pdf tex Notes on solutions to initial value problems pdf tex Topics and homework assignments Assigned homework problems may change up until a week before their due date. Assignments are taken from texts by Banchoff and Lovett (B&L) and Shifrin (S), unless otherwise noted. Topics and assignments through spring break (April 24) Solutions to first exam Solutions to second exam Solutions to third exam April 26-28: Parallel transport, geodesics. Read B&L 8.1-8.2; S2.4. Homework due Tuesday May 3: B&L 8.1.4, 8.2.10 S2.4: 1, 2, 4, 6, 11, 15, 20 Bonus: Figure out what map projection is used in the graphic here. (A Facebook account is not needed.) May 3-5: Local and global Gauss-Bonnet theorem. Read B&L 8.4; S3.1. Homework due Tuesday May 10: B&L: 8.1.8, 8.4.5, 8.4.6 S3.1: 2, 4, 5, 8, 9 Project assignment: Submit final version of paper electronically to me BY FRIDAY MAY 13. May 10: Hyperbolic geometry. Read B&L 8.5; S3.2. No homework this week. Third exam: May 12 (in class) Take-home exam: due May 19 (at presentation of final projects) Instructors for MAT 362 Differential Geometry, Spring 2011 Joshua Bowman (main instructor) Office: Math Tower 3-114 Office hours: Monday 4:00-5:00, Friday 9:30-10:30 Email: joshua dot bowman at gmail dot com Lloyd Smith (grader Feb. -

History of Mathematics
Georgia Department of Education History of Mathematics K-12 Mathematics Introduction The Georgia Mathematics Curriculum focuses on actively engaging the students in the development of mathematical understanding by using manipulatives and a variety of representations, working independently and cooperatively to solve problems, estimating and computing efficiently, and conducting investigations and recording findings. There is a shift towards applying mathematical concepts and skills in the context of authentic problems and for the student to understand concepts rather than merely follow a sequence of procedures. In mathematics classrooms, students will learn to think critically in a mathematical way with an understanding that there are many different ways to a solution and sometimes more than one right answer in applied mathematics. Mathematics is the economy of information. The central idea of all mathematics is to discover how knowing some things well, via reasoning, permit students to know much else—without having to commit the information to memory as a separate fact. It is the reasoned, logical connections that make mathematics coherent. The implementation of the Georgia Standards of Excellence in Mathematics places a greater emphasis on sense making, problem solving, reasoning, representation, connections, and communication. History of Mathematics History of Mathematics is a one-semester elective course option for students who have completed AP Calculus or are taking AP Calculus concurrently. It traces the development of major branches of mathematics throughout history, specifically algebra, geometry, number theory, and methods of proofs, how that development was influenced by the needs of various cultures, and how the mathematics in turn influenced culture. The course extends the numbers and counting, algebra, geometry, and data analysis and probability strands from previous courses, and includes a new history strand. -

A Comparison of Differential Calculus and Differential Geometry in Two
1 A Two-Dimensional Comparison of Differential Calculus and Differential Geometry Andrew Grossfield, Ph.D Vaughn College of Aeronautics and Technology Abstract and Introduction: Plane geometry is mainly the study of the properties of polygons and circles. Differential geometry is the study of curves that can be locally approximated by straight line segments. Differential calculus is the study of functions. These functions of calculus can be viewed as single-valued branches of curves in a coordinate system where the horizontal variable controls the vertical variable. In both studies the derivative multiplies incremental changes in the horizontal variable to yield incremental changes in the vertical variable and both studies possess the same rules of differentiation and integration. It seems that the two studies should be identical, that is, isomorphic. And, yet, students should be aware of important differences. In differential geometry, the horizontal and vertical units have the same dimensional units. In differential calculus the horizontal and vertical units are usually different, e.g., height vs. time. There are differences in the two studies with respect to the distance between points. In differential geometry, the Pythagorean slant distance formula prevails, while in the 2- dimensional plane of differential calculus there is no concept of slant distance. The derivative has a different meaning in each of the two subjects. In differential geometry, the slope of the tangent line determines the direction of the tangent line; that is, the angle with the horizontal axis. In differential calculus, there is no concept of direction; instead, the derivative describes a rate of change. In differential geometry the line described by the equation y = x subtends an angle, α, of 45° with the horizontal, but in calculus the linear relation, h = t, bears no concept of direction. -

Differential Geometry: Curvature and Holonomy Austin Christian
University of Texas at Tyler Scholar Works at UT Tyler Math Theses Math Spring 5-5-2015 Differential Geometry: Curvature and Holonomy Austin Christian Follow this and additional works at: https://scholarworks.uttyler.edu/math_grad Part of the Mathematics Commons Recommended Citation Christian, Austin, "Differential Geometry: Curvature and Holonomy" (2015). Math Theses. Paper 5. http://hdl.handle.net/10950/266 This Thesis is brought to you for free and open access by the Math at Scholar Works at UT Tyler. It has been accepted for inclusion in Math Theses by an authorized administrator of Scholar Works at UT Tyler. For more information, please contact [email protected]. DIFFERENTIAL GEOMETRY: CURVATURE AND HOLONOMY by AUSTIN CHRISTIAN A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science Department of Mathematics David Milan, Ph.D., Committee Chair College of Arts and Sciences The University of Texas at Tyler May 2015 c Copyright by Austin Christian 2015 All rights reserved Acknowledgments There are a number of people that have contributed to this project, whether or not they were aware of their contribution. For taking me on as a student and learning differential geometry with me, I am deeply indebted to my advisor, David Milan. Without himself being a geometer, he has helped me to develop an invaluable intuition for the field, and the freedom he has afforded me to study things that I find interesting has given me ample room to grow. For introducing me to differential geometry in the first place, I owe a great deal of thanks to my undergraduate advisor, Robert Huff; our many fruitful conversations, mathematical and otherwise, con- tinue to affect my approach to mathematics. -

A Theorem on Holonomy
A THEOREM ON HOLONOMY BY W. AMBROSE AND I. M. SINGER Introduction. The object of this paper is to prove Theorem 2 of §2, which shows, for any connexion, how the curvature form generates the holonomy group. We believe this is an extension of a theorem stated without proof by E. Cartan [2, p. 4]. This theorem was proved after we had been informed of an unpublished related theorem of Chevalley and Koszul. We are indebted to S. S. Chern for many discussions of matters considered here. In §1 we give an exposition of some needed facts about connexions; this exposition is derived largely from an exposition of Chern [5 ] and partly from expositions of H. Cartan [3] and Ehresmann [7]. We believe this exposition does however contain one new element, namely Lemma 1 of §1 and its use in passing from H. Cartan's definition of a connexion (the definition given in §1) to E. Cartan's structural equation. 1. Basic concepts. We begin with some notions and terminology to be used throughout this paper. The term "differentiable" will always mean what is usually called "of class C00." We follow Chevalley [6] in general for the definition of tangent vector, differential, etc. but with the obvious changes needed for the differentiable (rather than analytic) case. However if <p is a differentiable mapping we use <j>again instead of d<f>and 8<(>for the induced mappings of tangent vectors and differentials. If AT is a manifold, by which we shall always mean a differentiable manifold but which is not assumed connected, and mGM, we denote the tangent space to M at m by Mm. -

20. Geometry of the Circle (SC)
20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord. -

Geometry Course Outline
GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid -
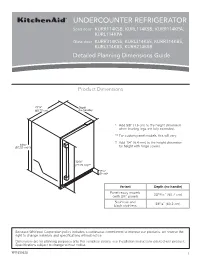
Dimension Guide
UNDERCOUNTER REFRIGERATOR Solid door KURR114KSB, KURL114KSB, KURR114KPA, KURL114KPA Glass door KURR314KSS, KURL314KSS, KURR314KBS, KURL314KBS, KURR214KSB Detailed Planning Dimensions Guide Product Dimensions 237/8” Depth (60.72 cm) (no handle) * Add 5/8” (1.6 cm) to the height dimension when leveling legs are fully extended. ** For custom panel models, this will vary. † Add 1/4” (6.4 mm) to the height dimension 343/8” (87.32 cm)*† for height with hinge covers. 305/8” (77.75 cm)** 39/16” (9 cm)* Variant Depth (no handle) Panel ready models 2313/16” (60.7 cm) (with 3/4” panel) Stainless and 235/8” (60.2 cm) black stainless Because Whirlpool Corporation policy includes a continuous commitment to improve our products, we reserve the right to change materials and specifications without notice. Dimensions are for planning purposes only. For complete details, see Installation Instructions packed with product. Specifications subject to change without notice. W11530525 1 Panel ready models Stainless and black Dimension Description (with 3/4” panel) stainless models A Width of door 233/4” (60.3 cm) 233/4” (60.3 cm) B Width of the grille 2313/16” (60.5 cm) 2313/16” (60.5 cm) C Height to top of handle ** 311/8” (78.85 cm) Width from side of refrigerator to 1 D handle – door open 90° ** 2 /3” (5.95 cm) E Depth without door 2111/16” (55.1 cm) 2111/16” (55.1 cm) F Depth with door 2313/16” (60.7 cm) 235/8” (60.2 cm) 7 G Depth with handle ** 26 /16” (67.15 cm) H Depth with door open 90° 4715/16” (121.8 cm) 4715/16” (121.8 cm) **For custom panel models, this will vary. -

Riemann's Contribution to Differential Geometry
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Historia Mathematics 9 (1982) l-18 RIEMANN'S CONTRIBUTION TO DIFFERENTIAL GEOMETRY BY ESTHER PORTNOY UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN, URBANA, IL 61801 SUMMARIES In order to make a reasonable assessment of the significance of Riemann's role in the history of dif- ferential geometry, not unduly influenced by his rep- utation as a great mathematician, we must examine the contents of his geometric writings and consider the response of other mathematicians in the years immedi- ately following their publication. Pour juger adkquatement le role de Riemann dans le developpement de la geometric differentielle sans etre influence outre mesure par sa reputation de trks grand mathematicien, nous devons &udier le contenu de ses travaux en geometric et prendre en consideration les reactions des autres mathematiciens au tours de trois an&es qui suivirent leur publication. Urn Riemann's Einfluss auf die Entwicklung der Differentialgeometrie richtig einzuschZtzen, ohne sich von seinem Ruf als bedeutender Mathematiker iiberm;issig beeindrucken zu lassen, ist es notwendig den Inhalt seiner geometrischen Schriften und die Haltung zeitgen&sischer Mathematiker unmittelbar nach ihrer Verijffentlichung zu untersuchen. On June 10, 1854, Georg Friedrich Bernhard Riemann read his probationary lecture, "iber die Hypothesen welche der Geometrie zu Grunde liegen," before the Philosophical Faculty at Gdttingen ill. His biographer, Dedekind [1892, 5491, reported that Riemann had worked hard to make the lecture understandable to nonmathematicians in the audience, and that the result was a masterpiece of presentation, in which the ideas were set forth clearly without the aid of analytic techniques.