DOCSLIB.ORG

3D Numerical Modeling of Forward Folding and Reverse Unfolding of a Viscous Single-Layer: Implications for the Formation of Folds and Fold Patterns ⁎ Stefan M

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
3D Numerical Modeling of Forward Folding and Reverse Unfolding of a Viscous Single-Layer: Implications for the Formation of Folds and Fold Patterns ⁎ Stefan M Available online at www.sciencedirect.com Tectonophysics 446 (2008) 31–41 www.elsevier.com/locate/tecto 3D numerical modeling of forward folding and reverse unfolding of a viscous single-layer: Implications for the formation of folds and fold patterns ⁎ Stefan M. Schmalholz Geological Institute, ETH Zurich, Switzerland Received 13 April 2007; received in revised form 24 September 2007; accepted 27 September 2007 Available online 6 October 2007 Abstract The main aims of this study are to show (i) that non-cylindrical three-dimensional (3D) fold shapes and patterns can form during a single, unidirectional shortening event and (ii) that numerical reverse modeling of 3D folding is a feasible method to reconstruct the formation of 3D buckle-folds. 3D viscous (Newtonian) single-layer folding is numerically simulated with the finite element method to investigate the formation of fold shapes during one shortening event. An initially flat layer rests on a matrix with smaller viscosity and is shortened in one direction parallel to the layering. Forward modeling with different initial geometrical perturbations on the flat layer and different lateral boundary conditions generates non-cylindrical 3D fold shapes and patterns. The simulations show that, in reality, the initial layer geometry and the boundary conditions strongly control the final fold geometry. Fold geometries produced from the forward folding models are used as initial setting in numerical reverse folding models with parameters identical to those of forward models. These reverse models accurately reconstruct the initial geometry of forward models with also only one extension event parallel to the previous shortening direction. The starting geometry of the forward models is inaccurately reconstructed by the reverse models if a significantly different viscosity ratio than in the forward models is used. This work demonstrates that reverse modeling has a high potential for reconstructing the deformation history of folded regions and rheological constraints such as viscosity ratio. Reverse models may be applied to natural 3D fold shapes and patterns in order to determine if they formed (i) during a single or multiple deformation events and (ii) as active buckle-folds with a viscosity ratio ≫ 1 or as passive, kinematic folds without buckling. This approach may find much application to fold interference patterns, in particular. © 2007 Elsevier B.V. All rights reserved. Keywords: Folding; Buckling; 3D; Reverse modeling; Interference patterns 1. Introduction tion may be unknown and also more than one shortening event with different shortening directions may have been active during A method to reconstruct fold amplification and especially to the formation of natural fold shapes. In this study, 3D numerical estimate the amount of bulk shortening that generated a viscous reverse modeling is presented as a potential tool for 3D fold (Newtonian) buckle-fold has been suggested for two dimensions reconstruction. In this context, the impact of (i) the initial (2D) (Schmalholz and Podladchikov, 2001; Schmalholz, 2006). perturbation geometry of the layer, (ii) the boundary conditions A main difficulty, which was solved with this method, is to and (iii) the viscosity ratio on 3D forward and reverse folding separate the amount of shortening by layer thickening from the models is investigated. The results have important implications amount of shortening by folding at constant layer thickness. This for the applicability of numerical reverse modeling to natural fold method can be applied in 3D for cylindrical fold shapes but not for shapes and patterns. more complex, non-cylindrical fold shapes. Additional difficul- In 3D, fold interference patterns have attracted considerable ties arise in 3D fold reconstruction because the shortening direc- attention because such patterns may provide insight into the deformation history of the rock, such as the number of ⁎ Tel.: +41 44 632 8167; fax: +41 44 632 1030. deformation phases, the shortening direction and the amount of E-mail address: [email protected]. bulk shortening. 3D fold interference patterns have been studied 0040-1951/$ - see front matter © 2007 Elsevier B.V. All rights reserved. doi:10.1016/j.tecto.2007.09.005 32 S.M. Schmalholz / Tectonophysics 446 (2008) 31–41 with two fundamentally different underlying assumptions: demonstrated by an experiment of G.I. Taylor (see Taylor and passive or active folding. In passive folding, the folded layers Friedman, 1966). On the other hand, it was shown that low exhibit no competence contrast (e.g., the Newtonian viscosity of Reynolds number flows exhibiting contrasts in material the layer and the matrix are identical) and, therefore, no properties (e.g., particles in shear flow) can exhibit chaotic mechanical instability is involved (Odriscoll, 1962; Ramsay, advection and are not reversible (e.g., Aref, 1984; Yarin et al., 1962; Thiessen and Means, 1980; Ramsay and Huber, 1987). 1997; Pine et al., 2005). For folding, an advection equation must Hence, no wavelength selection process is active and it is difficult be solved in addition to the Stokes equations to move the layer to explain what mechanism has actually generated the often interfaces through the model domain during shortening. The observed regularity and periodicity in natural folds. In active reversibility is not obvious because the viscous flow moving the folding, the folded layers possess a higher competence than the layer interfaces is unsteady (due to the moving boundaries and embedding material and a buckling instability with its corres- the buckling instability), and the viscous flow is sensitive to ponding wavelength selection process is active (Ghosh and small changes in the shape of the layer interfaces. Therefore, the Ramberg, 1968; Skjernaa, 1975; Grujic, 1993; Johns and Mosher, numerical simulations performed in this study have their 1996; Kaus and Schmalholz, 2006). In this study, only active justification in showing the numerical reversibility for high folding generated by a mechanical instability is considered. amplitude 3D viscous folding. Important questions arising while studying 3D fold shapes The applicability of the reverse folding modeling indicates that are how many deformation events have generated the observed it is useful to apply numerical models to reverse the formation of fold geometries and how much bulk shortening took place. 3D fold shapes that were generated by a mechanical instability. Numerical simulations of single-layer folding performed in this However, for practical fold reconstructions, the viscosity ratio study show that non-cylindrical 3D fold shapes, with curved between layer and matrix can only be roughly estimated for fold axes and axes orientations varying up to 90°, can be natural folds, and therefore the impact of uncertainties in viscosity generated during a single shortening event with one constant ratios on the reverse models are quantified in this study. The shortening direction. The simulations show that this is possible results show that reverse modeling can be used to test whether because the final fold shapes are strongly controlled by the fold shapes have been generated by either active or passive initial perturbation geometry of the layer (e.g., Mancktelow, folding and may have a high potential to determine whether fold 2001) and the boundary conditions. Therefore, fold shapes with shapes have been generated by one or more deformation events. strongly varying fold axes can be generated by (i) a single, The aims of the paper are (i) to show that 3D fold geometries unidirectional shortening event, (ii) a single, multidirectional with significantly varying fold axes can be generated by single, shortening event (e.g., constriction), or (iii) two or more unidirectional shortening events, (ii) to test the feasibility of shortening events (i.e. true superposed folds). numerical reverse modeling for 3D fold reconstruction and (iii) A suitable tool to investigate the shortening events to quantify the impact of different viscosity ratios on the retro- generating 3D fold shapes and to reconstruct the evolution of deformation of 3D fold shapes. 3D fold patterns is numerical modeling. Alternatively, existing analytical solutions for 3D single-layer folding could be used 2. Methods (e.g., Fletcher, 1991) but these analytical solutions are only valid for small amplitudes and limb dips. In this study numerical The numerical algorithm applied in this work for forward and models are applied because (i) high amplitude folds are reverse modeling is self-developed and the finite element method investigated and (ii) the numerical models can easily be used is employed to solve the continuum mechanics equations for slow in the future for more complex scenarios such as multilayers or viscous (Newtonian), incompressible flow in 3D in the absence of layers with strongly variable thickness. Usually, numerical gravity (see Appendix). The boundary conditions applied for all models are used to simulate the formation of buckle-folds during the shortening of stiff layers (Kaus and Schmalholz, 2006); they are referred to as forward models. On the other hand, it is also possible to use the fold geometries as initial setting of a numerical model and extend the model in a direction opposite to the shortening direction used to produce the folds. Such models are referred to as reverse models. Reverse modeling has been for example applied to Rayleigh–Taylor instabilities (Kaus and Podladchikov, 2001) and flanking
Load more

Recommended publications
  • Poster Final
    Evidence for polyphase deformation in the mylonitic zones bounding the Chester and Athens Domes, in southeastern Vermont, from 40Ar/39Ar geochronology Schnalzer, K., Webb, L., McCarthy, K., University of Vermont Department of Geology, Burlington Vermont, USA CLM 40 39 Sample Mineral Assemblage Metamorphic Facies Abstract Microstructure and Ar/ Ar Geochronology 18CD08A Quartz, Muscovite, Biotite, Feldspar, Epidote Upper Greenschist to Lower Amphibolite The Chester and Athens Domes are a composite mantled gneiss QC Twelve samples were collected during the fall of 2018 from the shear zones bounding the Chester and Athens Domes for 18CD08B Quartz, Biotite, Feldspar, Amphibole Amphibolite Facies 18CD08C Quartz, Muscovite, Biotite, Feldspar, Epidote Upper Greenschist to Lower Amphibolite dome in southeast Vermont. While debate persists regarding Me 40 39 microstructural analysis and Ar/ Ar age dating. These samples were divided between two transects, one in the northeastern 18CD08D Quartz, Muscovite, Biotite, Feldspar, Garnet Upper Greenschist to Lower Amphibolite the mechanisms of dome formation, most workers consider the VT NH section of the Chester dome and the second in the southern section of the Athens dome. These samples were analyzed by X-ray 18CD08E Quartz, Muscovite Greenschist Facies domes to have formed during the Acadian Orogeny. This study diraction in the fall of 2018. Oriented, orthogonal thin sections were also prepared for each of the twelve samples. The thin sec- 18CD09A Quartz, Amphibole Amphib olite Facies 40 CVGT integrates the results of Ar/Ar step-heating of single mineral NY tions named with an “X” were cut parallel to the stretching lineation (X) and normal to the foliation (Z) whereas the thin sections 18CD09B Quartz, Biotite, Feldspar, Amphibole, Muscovite Amphibolite Facies grains, or small multigrain aliquots, with data from microstruc- 18CD09C Quartz, Amphibole, Feldspar Amphibolite Facies named with a “Y” have been cut perpendicular to the ‘X-Z’ thin section.
    [Show full text]
  • Sedimentary Record of Cretaceous And
    SEDIMENT AR Y RECORD OF CRETACEOUS AND TER TIAR Y SALT MOVEMENT, EAST TEXAS BASIN: TIMES, RATES, AND LUMES OF SALT FLOW, IMPLICATIONS TO NUCLEAR-WA TE ISOLATION AND PETROLEUM EXPLO ATION by Steven J. Seni and M. P. A. ackson This work was supported by U.S. Depart ent of Energy and funded under Contract No. DE-AC 7-80ET46617 CONTENTS ABSTRACT . • 00 INTRODUCTION. • 00 Data Base. • 00 Early History of Basin Formation and Infilling • 00 Geometry of Salt Structures • 00 EVOLUTIONARY STAGES OF DOME GROWTH. • 00 Pillow Stage . • 00 Geometry of Overlying Strata . • 00 Geometry of Surrounding Strata • 00 Depositional Facies and Lithostratigraph • 00 Diapir Stage • • 00 Geometry of Surrounding Strata • 00 Depositional Facies and Lithostratigraph • 00 Post-Diapir Stage • 00 Geometry of Surrounding Strata • 00 Depositional Facies and Lithostratigraphy • 00 Holocene Analogues. • 00 Discussion • 00 Significance to Subtle Petroleum Traps • 00 PATTERNS OF SALT MOVEMENT IN TIME AND SPAC • 00 Group 1: Pre-Glen Rose Subgroup (pre-112 Ma) - Periphery of Diapir Province • • 00 Group 2: Glen Rose Subgroup to Washita Group 112 to 98 Ma)-­ Basin Axis • 00 Group 3: Post-Austin Group (86 to 56 Ma) -- Per phery of Diapir Province • • 00 Initiation and Acceleration of Salt Flow • • 00 Overview of Dome History • • 00 RATES OF SALT MOVEMENT AND DOME GROWTH • • 00 Assumptions • • 00 Proven Propositions. • 00 Unproven Propositions • 00 Incorrect Propositions • • 00 Distinguishing Between Syndepositional and Post-D positional Thickness Variations. • 00 The Problem • • 00 Structural Evidence • • 00 Sedimentological Evidence • • 00 Methodology • • 00 Distinguishing Between Regional and Salt-Re ated Thickness Variations. • 00 Volume of Salt Mobilized and Estimates of S t Loss • 00 Rates of Dome Growth • • 00 Net Rates of Pillow Growth • 00 Net Rates of Diapir Growth • 00 Gross Rates of Diapir Growth • • 00 Growth Rates and Strain Rates • 00 IMPLICA TIONS TO WASTE ISOLATION • • 00 CONCLUSIONS • • 00 ACKNOWLEDGMENTS • • 00 REFERENCES • 00 APPENDICES • 00 Figures 1.
    [Show full text]
  • Part 3: Normal Faults and Extensional Tectonics
    12.113 Structural Geology Part 3: Normal faults and extensional tectonics Fall 2005 Contents 1 Reading assignment 1 2 Growth strata 1 3 Models of extensional faults 2 3.1 Listric faults . 2 3.2 Planar, rotating fault arrays . 2 3.3 Stratigraphic signature of normal faults and extension . 2 3.4 Core complexes . 6 4 Slides 7 1 Reading assignment Read Chapter 5. 2 Growth strata Although not particular to normal faults, relative uplift and subsidence on either side of a surface breaking fault leads to predictable patterns of erosion and sedi­ mentation. Sediments will fill the available space created by slip on a fault. Not only do the characteristic patterns of stratal thickening or thinning tell you about the 1 Figure 1: Model for a simple, planar fault style of faulting, but by dating the sediments, you can tell the age of the fault (since sediments were deposited during faulting) as well as the slip rates on the fault. 3 Models of extensional faults The simplest model of a normal fault is a planar fault that does not change its dip with depth. Such a fault does not accommodate much extension. (Figure 1) 3.1 Listric faults A listric fault is a fault which shallows with depth. Compared to a simple planar model, such a fault accommodates a considerably greater amount of extension for the same amount of slip. Characteristics of listric faults are that, in order to maintain geometric compatibility, beds in the hanging wall have to rotate and dip towards the fault. Commonly, listric faults involve a number of en echelon faults that sole into a low­angle master detachment.
    [Show full text]
  • Influences of Surface Processes on Fold Growth During 3D Detachment
    PUBLICATIONS Geochemistry, Geophysics, Geosystems RESEARCH ARTICLE Influences of surface processes on fold growth during 3-D 10.1002/2014GC005450 detachment folding Key Point: M. Collignon1, B. J. P. Kaus2, D. A. May3, and N. Fernandez2 Influences of surface processes on the fold pattern in fold-and-thrust 1Geological Institute, ETH Zurich, Zurich, Switzerland, 2Institut fur€ Geowissenschaften, Johannes Gutenberg-Universit€at, belts Mainz, Germany, 3Institute of Geophysics, ETH Zurich, Zurich, Switzerland Correspondence to: M. Collignon, Abstract In order to understand the interactions between surface processes and multilayer folding sys- [email protected] tems, we here present fully coupled three-dimensional numerical simulations. The mechanical model repre- sents a sedimentary cover with internal weak layers, detached over a much weaker basal layer representing Citation: salt or evaporites. Applying compression in one direction results in a series of three-dimensional buckle folds, Collignon, M., B. J. P. Kaus, D. A. May, and N. Fernandez (2014), Influences of of which the topographic expression consists of anticlines and synclines. This topography is modified through surface processes on fold growth time by mass redistribution, which is achieved by a combination of fluvial and hillslope erosion, as well as during 3-D detachment folding, deposition, and which can in return influence the subsequent deformation. Model results show that surface Geochem. Geophys. Geosyst., 15, doi:10.1002/2014GC005450. processes do not have a significant influence on folding patterns and aspect ratio of the folds. Nevertheless, erosion reduces the amount of shortening required to initiate folding and increases the exhumation rates. Received 9 JUN 2014 Increased sedimentation in the synclines contributes to this effect by amplifying the fold growth rate by grav- Accepted 29 JUL 2014 ity.
    [Show full text]
  • Tectonics of the Musandam Peninsula and Northern Oman Mountains: from Ophiolite Obduction to Continental Collision
    GeoArabia, 2014, v. 19, no. 2, p. 135-174 Gulf PetroLink, Bahrain Tectonics of the Musandam Peninsula and northern Oman Mountains: From ophiolite obduction to continental collision Michael P. Searle, Alan G. Cherry, Mohammed Y. Ali and David J.W. Cooper ABSTRACT The tectonics of the Musandam Peninsula in northern Oman shows a transition between the Late Cretaceous ophiolite emplacement related tectonics recorded along the Oman Mountains and Dibba Zone to the SE and the Late Cenozoic continent-continent collision tectonics along the Zagros Mountains in Iran to the northwest. Three stages in the continental collision process have been recognized. Stage one involves the emplacement of the Semail Ophiolite from NE to SW onto the Mid-Permian–Mesozoic passive continental margin of Arabia. The Semail Ophiolite shows a lower ocean ridge axis suite of gabbros, tonalites, trondhjemites and lavas (Geotimes V1 unit) dated by U-Pb zircon between 96.4–95.4 Ma overlain by a post-ridge suite including island-arc related volcanics including boninites formed between 95.4–94.7 Ma (Lasail, V2 unit). The ophiolite obduction process began at 96 Ma with subduction of Triassic–Jurassic oceanic crust to depths of > 40 km to form the amphibolite/granulite facies metamorphic sole along an ENE- dipping subduction zone. U-Pb ages of partial melts in the sole amphibolites (95.6– 94.5 Ma) overlap precisely in age with the ophiolite crustal sequence, implying that subduction was occurring at the same time as the ophiolite was forming. The ophiolite, together with the underlying Haybi and Hawasina thrust sheets, were thrust southwest on top of the Permian–Mesozoic shelf carbonate sequence during the Late Cenomanian–Campanian.
    [Show full text]
  • Plate Tectonics
    Plate Tectonics Plate Tectonics is a unifying theory that states that the Earth is composed of lithospheric crustal plates that move slowly, change size, and interact with one another. This theory was amalgamated from a variety of studies that began in the early 20th century and culminated in the 1960s. Early Players: Richard Oldham (1858-1936): discovered P Wave Shadow Zones Inge Lehmann (1888-1993): discovered the S Wave Shadow Zone, including the fact that the outer core is liquid Eduard Suess (1831-1914): published internal structure of the Earth, utilizing some of Oldham’s data Andrija Mohorovicic (1857-1936): discovered the seismic discontinuity between the crust and the mantle Beno Gutenberg (1889-1960): found the CMB to be at 2900 km The Great Synthesizer: Alfred Wagener (1880-1930) Book: The Origin of Continents and Oceans (1915) Found six major pieces of evidence the continents move, hence his theory is known as Continental Drift. (Figures 19.2-1911) 1) The shape of the continents: they fit together 2) Paleontological Evidence: found matching fossils on several continents a) Glossopteris: found in rocks of the same age on South America, South Africa, Australia, India and Antarctica b) Lystrosaurus: found in rocks of the same age on Africa, India, also some in Asia and Antarctica c) Mesosaurus: found in rocks of the same age on South America, South Africa d) Cynognathus: found in rocks of the same age on South America, South Africa 3) Glacial Evidence: the glaciers appear to originate from the modern-day oceans (which is impossible) 4) Structure and Rock Type: geologic features end on one continent and reappear on the other (South America and Africa) 5) Paleoclimate Zones: like today, the old Earth had climate zones.
    [Show full text]
  • THE JOURNAL of GEOLOGY March 1990
    VOLUME 98 NUMBER 2 THE JOURNAL OF GEOLOGY March 1990 QUANTITATIVE FILLING MODEL FOR CONTINENTAL EXTENSIONAL BASINS WITH APPLICATIONS TO EARLY MESOZOIC RIFTS OF EASTERN NORTH AMERICA' ROY W. SCHLISCHE AND PAUL E. OLSEN Department of Geological Sciences and Lamont-Doherty Geological Observatory of Columbia University, Palisades, New York 10964 ABSTRACT In many half-graben, strata progressively onlap the hanging wall block of the basins, indicating that both the basins and their depositional surface areas were growing in size through time. Based on these con- straints, we have constructed a quantitative model for the stratigraphic evolution of extensional basins with the simplifying assumptions of constant volume input of sediments and water per unit time, as well as a uniform subsidence rate and a fixed outlet level. The model predicts (1) a transition from fluvial to lacustrine deposition, (2) systematically decreasing accumulation rates in lacustrine strata, and (3) a rapid increase in lake depth after the onset of lacustrine deposition, followed by a systematic decrease. When parameterized for the early Mesozoic basins of eastern North America, the model's predictions match trends observed in late Triassic-age rocks. Significant deviations from the model's predictions occur in Early Jurassic-age strata, in which markedly higher accumulation rates and greater lake depths point to an increased extension rate that led to increased asymmetry in these half-graben. The model makes it possible to extract from the sedimentary record those events in the history of an extensional basin that are due solely to the filling of a basin growing in size through time and those that are due to changes in tectonics, climate, or sediment and water budgets.
    [Show full text]
  • Tectonic Features of the Precambrian Belt Basin and Their Influence on Post-Belt Structures
    ... Tectonic Features of the .., Precambrian Belt Basin and Their Influence on Post-Belt Structures GEOLOGICAL SURVEY PROFESSIONAL PAPER 866 · Tectonic Features of the · Precambrian Belt Basin and Their Influence on Post-Belt Structures By JACK E. HARRISON, ALLAN B. GRIGGS, and JOHN D. WELLS GEOLOGICAL SURVEY PROFESSIONAL PAPER X66 U N IT ED STATES G 0 V ERN M EN T P R I NT I N G 0 F F I C E, \VAS H I N G T 0 N 19 7 4 UNITED STATES DEPARTMENT OF THE INTERIOR ROGERS C. B. MORTON, Secretary GEOLOGICAL SURVEY V. E. McKelvey, Director Library of Congress catalog-card No. 74-600111 ) For sale by the Superintendent of Documents, U.S. GO\·ernment Printing Office 'Vashington, D.C. 20402 - Price 65 cents (paper cO\·er) Stock Number 2401-02554 CONTENTS Page Page Abstract................................................. 1 Phanerozoic events-Continued Introduction . 1 Late Mesozoic through early Tertiary-Continued Genesis and filling of the Belt basin . 1 Idaho batholith ................................. 7 Is the Belt basin an aulacogen? . 5 Boulder batholith ............................... 8 Precambrian Z events . 5 Northern Montana disturbed belt ................. 8 Phanerozoic events . 5 Tectonics along the Lewis and Clark line .............. 9 Paleozoic through early Mesozoic . 6 Late Cenozoic block faults ........................... 13 Late Mesozoic through early Tertiary . 6 Conclusions ............................................. 13 Kootenay arc and mobile belt . 6 References cited ......................................... 14 ILLUSTRATIONS Page FIGURES 1-4. Maps: 1. Principal basins of sedimentation along the U.S.-Canadian Cordillera during Precambrian Y time (1,600-800 m.y. ago) ............................................................................................... 2 2. Principal tectonic elements of the Belt basin reentrant as inferred from the sedimentation record ............
    [Show full text]
  • Pan-African Orogeny 1
    Encyclopedia 0f Geology (2004), vol. 1, Elsevier, Amsterdam AFRICA/Pan-African Orogeny 1 Contents Pan-African Orogeny North African Phanerozoic Rift Valley Within the Pan-African domains, two broad types of Pan-African Orogeny orogenic or mobile belts can be distinguished. One type consists predominantly of Neoproterozoic supracrustal and magmatic assemblages, many of juvenile (mantle- A Kröner, Universität Mainz, Mainz, Germany R J Stern, University of Texas-Dallas, Richardson derived) origin, with structural and metamorphic his- TX, USA tories that are similar to those in Phanerozoic collision and accretion belts. These belts expose upper to middle O 2005, Elsevier Ltd. All Rights Reserved. crustal levels and contain diagnostic features such as ophiolites, subduction- or collision-related granitoids, lntroduction island-arc or passive continental margin assemblages as well as exotic terranes that permit reconstruction of The term 'Pan-African' was coined by WQ Kennedy in their evolution in Phanerozoic-style plate tectonic scen- 1964 on the basis of an assessment of available Rb-Sr arios. Such belts include the Arabian-Nubian shield of and K-Ar ages in Africa. The Pan-African was inter- Arabia and north-east Africa (Figure 2), the Damara- preted as a tectono-thermal event, some 500 Ma ago, Kaoko-Gariep Belt and Lufilian Arc of south-central during which a number of mobile belts formed, sur- and south-western Africa, the West Congo Belt of rounding older cratons. The concept was then extended Angola and Congo Republic, the Trans-Sahara Belt of to the Gondwana continents (Figure 1) although West Africa, and the Rokelide and Mauretanian belts regional names were proposed such as Brasiliano along the western Part of the West African Craton for South America, Adelaidean for Australia, and (Figure 1).
    [Show full text]
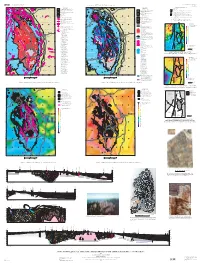
  • Map Showing Geology, Structure, and Geophysics of the Central Black
    U.S. DEPARTMENT OF THE INTERIOR Prepared in cooperation with the SCIENTIFIC INVESTIGATIONS MAP 2777 U.S. GEOLOGICAL SURVEY SOUTH DAKOTA SCHOOL OF MINES AND TECHNOLOGY FOUNDATION SHEET 2 OF 2 Pamphlet accompanies map 104°00' 103°30' 103°00' 104°00' 103°30' 103°00' ° ° EXPLANATION FOR MAPS F TO H 44 30' 44°30' EXPLANATION 44 30' 44°30' EXPLANATION Spearfish Geologic features 53 54 Tertiary igneous rocks (Tertiary and post-Tertiary Spearfish PHANEROZOIC ROCKS 90 1 90 sedimentary rocks not shown) Pringle fault 59 Tertiary igneous rocks (Tertiary and post-Tertiary Pre-Tertiary and Cretaceous (post-Inyan Kara sedimentary rocks not shown) Monocline—BHM, Black Hills monocline; FPM, Fanny Peak monocline 52 85 Group) rocks 85 Sturgis Sturgis Pre-Tertiary and Cretaceous (post-Inyan Kara A Proposed western limit of Early Proterozoic rocks in subsurface 55 Lower Cretaceous (Inyan Kara Group), Jurassic, Group) rocks 57 58 60 14 and Triassic rocks 14 Lower Cretaceous (Inyan Kara Group), Jurassic, B Northern extension (fault?) of Fanny Peak monocline and Triassic rocks Paleozoic rocks C Possible eastern limit of Early Proterozoic rocks in subsurface 50 Paleozoic rocks Precambrian rocks S Possible suture in subsurface separating different tectonic terranes 89 51 89 2 PRECAMBRIAN ROCKS of Sims (1995) 49 Contact St 3 G Harney Peak Granite (unit Xh) Geographic features—BL, Bear Lodge Mountains; BM, Bear Mountain; Fault—Dashed where approximately located G DT DT, Devils Tower 48 B Early Proterozoic rocks, undivided Anticline—Showing trace of axial surface and 1 St Towns and cities—B, Belle Fourche; C, Custer; E, Edgemont; HS, Hot direction of plunge.
    [Show full text]
  • Collision Orogeny
    Downloaded from http://sp.lyellcollection.org/ by guest on October 6, 2021 PROCESSES OF COLLISION OROGENY Downloaded from http://sp.lyellcollection.org/ by guest on October 6, 2021 Downloaded from http://sp.lyellcollection.org/ by guest on October 6, 2021 Shortening of continental lithosphere: the neotectonics of Eastern Anatolia a young collision zone J.F. Dewey, M.R. Hempton, W.S.F. Kidd, F. Saroglu & A.M.C. ~eng6r SUMMARY: We use the tectonics of Eastern Anatolia to exemplify many of the different aspects of collision tectonics, namely the formation of plateaux, thrust belts, foreland flexures, widespread foreland/hinterland deformation zones and orogenic collapse/distension zones. Eastern Anatolia is a 2 km high plateau bounded to the S by the southward-verging Bitlis Thrust Zone and to the N by the Pontide/Minor Caucasus Zone. It has developed as the surface expression of a zone of progressively thickening crust beginning about 12 Ma in the medial Miocene and has resulted from the squeezing and shortening of Eastern Anatolia between the Arabian and European Plates following the Serravallian demise of the last oceanic or quasi- oceanic tract between Arabia and Eurasia. Thickening of the crust to about 52 km has been accompanied by major strike-slip faulting on the rightqateral N Anatolian Transform Fault (NATF) and the left-lateral E Anatolian Transform Fault (EATF) which approximately bound an Anatolian Wedge that is being driven westwards to override the oceanic lithosphere of the Mediterranean along subduction zones from Cephalonia to Crete, and Rhodes to Cyprus. This neotectonic regime began about 12 Ma in Late Serravallian times with uplift from wide- spread littoral/neritic marine conditions to open seasonal wooded savanna with coiluvial, fluvial and limnic environments, and the deposition of the thick Tortonian Kythrean Flysch in the Eastern Mediterranean.
    [Show full text]
  • Faulted Joints: Kinematics, Displacement±Length Scaling Relations and Criteria for Their Identi®Cation
    Journal of Structural Geology 23 (2001) 315±327 www.elsevier.nl/locate/jstrugeo Faulted joints: kinematics, displacement±length scaling relations and criteria for their identi®cation Scott J. Wilkinsa,*, Michael R. Grossa, Michael Wackera, Yehuda Eyalb, Terry Engelderc aDepartment of Geology, Florida International University, Miami, FL 33199, USA bDepartment of Geology, Ben Gurion University, Beer Sheva 84105, Israel cDepartment of Geosciences, The Pennsylvania State University, University Park, PA 16802, USA Received 6 December 1999; accepted 6 June 2000 Abstract Structural geometries and kinematics based on two sets of joints, pinnate joints and fault striations, reveal that some mesoscale faults at Split Mountain, Utah, originated as joints. Unlike many other types of faults, displacements (D) across faulted joints do not scale with lengths (L) and therefore do not adhere to published fault scaling laws. Rather, fault size corresponds initially to original joint length, which in turn is controlled by bed thickness for bed-con®ned joints. Although faulted joints will grow in length with increasing slip, the total change in length is negligible compared to the original length, leading to an independence of D from L during early stages of joint reactivation. Therefore, attempts to predict fault length, gouge thickness, or hydrologic properties based solely upon D±L scaling laws could yield misleading results for faulted joints. Pinnate joints, distinguishable from wing cracks, developed within the dilational quadrants along faulted joints and help to constrain the kinematics of joint reactivation. q 2001 Elsevier Science Ltd. All rights reserved. 1. Introduction impact of these ªfaulted jointsº on displacement±length scaling relations and fault-slip kinematics.
    [Show full text]