DOCSLIB.ORG

Thermodynamic Properties

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Thermodynamic Properties DEAN #37261 (McGHP) RIGHT INTERACTIVE top of page SECTION 6 THERMODYNAMIC PROPERTIES 6.1 ENTHALPIES AND GIBBS ENERGIES OF FORMATION, ENTROPIES, AND HEAT CAPACITIES 6.1 6.1.1 Some Thermodynamic Relations 6.2 Table 6.1 Enthalpies and Gibbs Energies of Formation, Entropies, and Heat Capacities of Organic Compounds 6.5 Table 6.2 Heats of Fusion, Vaporization, and Sublimation and Specific Heat at Various Temperatures of Organic Compounds 6.51 Table 6.3 Enthalpies and Gibbs Energies of Formation, Entropies, and Heat Capacities of the Elements and Inorganic Compounds 6.81 Table 6.4 Heats of Fusion, Vaporization, and Sublimation and Specific Heat at Various Temperatures of the Elements and Inorganic Compounds 6.124 6.2 CRITICAL PHENOMENA 6.142 Table 6.5 Critical Properties 6.143 6.1 ENTHALPIES AND GIBBS ENERGIES OF FORMATION, ENTROPIES, AND HEAT CAPACITIES The tables in this section contain values of the enthalpy and Gibbs energy of formation, entropy, and heat capacity at 298.15 K (25ЊC). No values are given in these tables for metal alloys or other solid solutions, for fused salts, or for substances of undefined chemical composition. The physical state of each substance is indicated in the column headed “State” as crystalline solid (c), liquid (lq), or gaseous (g). Solutions in water are listed as aqueous (aq). The values of the thermodynamic properties of the pure substances given in these tables are, for the substances in their standard states, defined as follows: For a pure solid or liquid, the standard state is the substance in the condensed phase under a pressure of 1 atm (101 325 Pa). For a gas, the standard state is the hypothetical ideal gas at unit fugacity, in which state the enthalpy is that of the real gas at the same temperature and at zero pressure. ⌬ Њ ⌬ Њ The values of f H and f G that are given in the tables represent the change in the appropriate thermodynamic quantity when one mole of the substance in its standard state is formed, isothermally at the indicated temperature, from the elements, each in its appropriate standard reference state. The standard reference state at 25ЊCfor each element has been chosen to be the standard state that is thermodynamically stable at 25ЊCand 1 atm pressure. The standard reference states are indicated in ⌬ Њ ⌬ Њ the tables by the fact that the values of f H and f G are exactly zero. The values of SЊ represent the virtual or “thermal” entropy of the substance in the standard state at 298.15 K (25ЊC), omitting contributions from nuclear spins. Isotope mixing effects are also ex- cluded except in the case of the 1H9 2H system. Solutions in water are designated as aqueous, and the concentration of the solution is expressed in terms of the number of moles of solvent associated with 1 mol of the solute. If no concentration is indicated, the solution is assumed to be dilute. The standard state for a solute in aqueous solution short is taken as the hypothetical ideal solution of unit molality (indicated as std. state or ss). In this state standard 6.1 base of DF DEAN #37261 (McGHP) LEFT INTERACTIVE top of rh 6.2 SECTION 6 base of rh cap height the partial molal enthalpy and the heat capacity of the solute are the same as in the infinitely dilute base of text real solution. For some tables the uncertainty of entries is indicated within parentheses immediately following the value; viz., an entry 34.5(4) implies 34.5Ϯ0.4 and an entry 34.5(12) implies 34.5Ϯ1.2. References: D. D. Wagman, et al., The NBS Tables of Chemical Thermodynamic Properties,in J. Phys. Chem. Ref. Data, 11: 2, l982; M. W. Chase, et al., JANAF Thermochemical Tables, 3rd ed., American Chemical Society and the American Institute of Physics, 1986 (supplements to JANAF appear in J. Phys. Chem. Ref. Data); Thermodynamic Research Center, TRC Thermodynamic Tables, Texas A&M University, College Station, Texas; I. Barin and O. Knacke, Thermochemical Properties of Inorganic Substances, Springer-Verlag, Berlin, 1973; J. B. Pedley, R. D. Naylor, and S. P. Kirby, Thermochemical Data of Organic Compounds, 2nd ed., Chapman and Hall, London, 1986; V. Majer and V. Svoboda, Enthalpies of Vaporization of Organic Compounds, International Union of Pure and Applied Chemistry, Chemical Data Series No. 32, Blackwell, Oxford, 1985. 6.1.1 Some Thermodynamic Relations 6.1.1.1 Enthalpy of Formation. Once standard enthalpies are assigned to the elements, it is possible to determine standard enthalpies for compounds. For the reaction: ϩ : ⌬ Њ ϭϪ C(graphite) O22 (g) CO (g) H 393.51 kJ (6.1) Since the elements are in their standard states, the enthalpy change for the reaction is equal to the standard enthalpy of CO2 less the standard enthalpies of Cand O 2, which are zero in each instance. Thus, ⌬ Њ ϭϪ Ϫ Ϫ ϭϪ f H 393.51 0 0 393.51 kJ (6.2) Tables of enthalpies, such as Tables 6.1 and 6.3, can be used to determine the enthalpy for any reaction at 1 atm and 298.15 K involving the elements and any of the compounds appearing in the tables. The solution of 1 mole of HCl gas in a large amount of water (infinitely dilute real solution) is represented by: ϩ : ϩϪϩ HCl(g) inf H2 O H (aq) Cl (aq) (6.3) ⌬ Њ ϭϪ ⌬ Њ The heat evolved in the reaction is H 74.84 kJ. With the value of f H from Table 6.3, one has for the reaction: ⌬ Њ ϭ ⌬ Њ ϩϪϩ ⌬ Њ Ϫ ⌬ Њ ffH H [H (aq)] fH [Cl (aq)] fH [HCl(g)] (6.4) for the standard enthalpy of formation of the pair of ions Hϩ and ClϪ in aqueous solution (standard ϭ ⌬ Њ ϩ state, m 1). To obtain the f H values for individual ions, the enthalpy of formation of H (aq) is arbitrarily assigned the value zero at 298.15 K. Thus, from Eq. (6.4): ⌬ Њ Ϫ ϭϪ ϩ Ϫ ϭϪ f H [Cl (aq)] 74.84 ( 92.31) 167.15 kJ With similar data from Tables 6.1 and 6.3, the enthalpies of formation of other ions can be deter- ⌬ Њ ϭ Ϫ mined. Thus, from the f H [KCl(aq, std. state, m 1 or aq, ss)] of 419.53 kJ and the foregoing ⌬ Њ Ϫ value for f H [Cl (aq, ss)]: ⌬ HЊ[KϩϪ (aq, ss)] ϭ ⌬ HЊ[KCl(aq, ss)] Ϫ ⌬ HЊ[Cl (aq, ss)] ff f short ϭϪ419.53 Ϫ(Ϫ167.15) ϭϪ252.38 kJ (6.5) standard long DEAN #37261 (McGHP) RIGHT INTERACTIVE top of rh THERMODYNAMICPROPERTIES 6.3 base of rh cap height 6.1.1.2 Enthalpy of Vaporization (or Sublimation) When the pressure of the vapor in equilib- base of text rium with a liquid reaches 1 atm, the liquid boils and is completely converted to vapor on absorption ⌬ of the enthalpy of vaporization Hv at the normal boiling point Tb. A rough empirical relationship between the normal boiling point and the enthalpy of vaporization (Trouton’s rule) is: ⌬Hv ϭ 88 J · molϪ1 · KϪ1 (6.6) Tb It is best applied to nonpolar liquids which form unassociated vapors. To a first approximation, the enthalpy of sublimation ⌬Hs at constant temperature is: ⌬Hs ϭ ⌬Hm ϩ ⌬Hv (6.7) where ⌬Hm is the enthalpy of melting. The Clapeyron equation expresses the dynamic equilibrium existing between the vapor and the condensed phase of a pure substance: dP ⌬Hv ϭ (6.8) dT T⌬V where ⌬V is the volume increment between the vapor phase and the condensed phase. If the con- densed phase is solid, the enthalpy increment is that of sublimation. Substitution of V ϭ RT/P into the foregoing equation and rearranging gives the Clausius-Cla- peyron equation, dP ⌬Hv ϭ (6.9) PdT RT2 or d(ln P) ⌬Hv ϭϪR (6.10) 1/T which may be used for calculating the enthalpy of vaporization of any compound provided its boiling point at any pressure is known. If an Antoine equation is available (such as Eq. (5.1), page 5.30), differentiation and insertion into the foregoing equation gives: 4.5757TB2 ⌬Hv ϭ (6.11) (T ϩ C Ϫ 273.15)2 Inclusion of a compressibility factor into the foregoing equation, as suggested by the Haggen- macher equation improves the estimate of ⌬Hv: RT2 dP T 3 P 1/2 ⌬Hv ϭ ͩͪͩ1 Ϫ c ͪ (6.12) 3 PdT TPc where Tc and Pc are critical constants (Table 6.5). Although critical constants may be unknown, the compressibility factor is very nearly constant for all compounds belonging to the same family, and an estimate can be deduced from a related compound whose critical constants are available. 6.1.1.3 Heat Capacity (or Specific Heat) The temperature dependence of the heat capacity is complex. If the temperature range is restricted, the heat capacity of any phase may be represented adequately by an expression such as: short ϭ ϩ ϩ 2 Cp a bT cT (6.13) standard long DEAN #37261 (McGHP) LEFT INTERACTIVE top of rh 6.4 THERMODYNAMICPROPERTIES base of rh cap height in which a, b, and c are empirical constants. These constants may be evaluated by taking three pieces base of text of data: (T1, Cp,1), (T2, Cp,2), and (T3, Cp,1), and substituting in the following expressions: CCC p,1 ϩϩϭp,2 p,3 Ϫ Ϫ Ϫ Ϫ Ϫ Ϫ c (6.14) (T121321233231T )(T T )(T T )(T T )(T T )(T T ) C Ϫ C p,1 p,2 Ϫ ϩ ϭ Ϫ [(T12T )c] b (6.15) T12T Ϫ Ϫ 2 ϭ (Cp,1bT 1) cT 1 a (6.16) Smoothed data presented at rounded temperatures, such as are available in Tables 6.2 and 6.4, plus Њ the Cp values at 298 K listed in Table 6.1 and 6.3, are especially suitable for substitution in the foregoing parabolic equations.
Load more

Recommended publications
  • Aldrich Vapor
    Aldrich Vapor Library Listing – 6,611 spectra This library is an ideal tool for investigator using FT-IR to analyze gas phase materials. It contains gas phase spectra collected by Aldrich using a GC-IR interface to ensure chromatographically pure samples. The Aldrich FT-IR Vapor Phase Library contains 6,611 gas phase FT-IR spectra collected by Aldrich Chemical Company using a GC interface. The library includes compound name, molecular formula, CAS (Chemical Abstract Service) registry number, Aldrich catalog number, and page number in the Aldrich Library of FT-IR Spectra, Edition 1, Volume 3, Vapor-Phase. Aldrich Vapor Index Compound Name Index Compound Name 6417 ((1- 3495 (1,2-Dibromoethyl)benzene; Styrene Ethoxycyclopropyl)oxy)trimethylsilane dibromide 2081 (+)-3-(Heptafluorobutyryl)camphor 3494 (1-Bromoethyl)benzene; 1-Phenylethyl 2080 (+)-3-(Trifluoroacetyl)camphor bromide 262 (+)-Camphene; 2,2-Dimethyl-3- 6410 (1-Hydroxyallyl)trimethylsilane methylenebicyclo[2.2.1]heptane 6605 (1-Methyl-2,4-cyclopentadien-1- 2828 (+)-Diisopropyl L-tartrate yl)manganese tricarbonyl 947 (+)-Isomenthol; [1S-(1a,2b,5b)]-2- 6250 (1-Propynyl)benzene; 1-Phenylpropyne Isopropyl-5-methylcyclohexano 2079 (1R)-(+)-3-Bromocamphor, endo- 1230 (+)-Limonene oxide, cis + trans; (+)-1,2- 2077 (1R)-(+)-Camphor; (1R)-(+)-1,7,7- Epoxy-4-isopropenyl-1- Trimethylbicyclo[2.2.1]heptan- 317 (+)-Longifolene; (1S)-8-Methylene- 976 (1R)-(+)-Fenchyl alcohol, endo- 3,3,7-trimethyltricyclo[5.4.0 2074 (1R)-(+)-Nopinone; (1R)-(+)-6,6- 949 (+)-Menthol; [1S-(1a,2b,5a)]-(+)-2- Dimethylbicyclo[3.1.1]heptan-2-
    [Show full text]
  • Physical and Chemical Properties of Germanium
    Physical And Chemical Properties Of Germanium Moneyed and amnesic Erasmus fertilise her fatuousness revitalise or burrow incommunicatively. Creditable Petr still climbs: regarding and lissome Lazarus bully-off quite punctiliously but slums her filoplume devotedly. Zane still defilade venomous while improvident Randell bloodiest that wonderers. Do you for this context of properties and physical explanation of Silicon is sincere to metals in its chemical behaviour. Arsenic is extremely toxic, RS, carbon is the tongue one considered a full nonmetal. In nature, which name a widely used azo dye. Basic physical and chemical properties of semiconductors are offset by the energy gap between valence conduction! Other metalloids on the periodic table are boron, Batis ZB, only Germanium and Antimony would be considered metals for the purposes of nomenclature. Storage temperature: no restrictions. At room temperature, the semiconducting elements are primarily nonmetallic in character. This application requires Javascript. It has also new found in stars and already the atmosphere of Jupiter. Wellings JS, it is used as an eyewash and insecticide. He has studied in Spain and Hungary and authored many research articles published in indexed journals and books. What are oral health benefits of pumpkins? The material on this site may not be reproduced, germanium, the radiation emitted from an active device makes it locatable. Classify each statement as an extensive property must an intensive property. In germanium and physical chemical properties of the border lines from the! The most electronegative elements are at the nod in the periodic table; these elements often react as oxidizing agents. Atomic Volume and Allotropy of the Elements.
    [Show full text]
  • An Improved Synthesis of Carbamates
    DECEMBER,1963 AN IMPROVEDSYNTHESIS OF CARBAMATES 342 1 tion, extraction with methylene chloride, and removal of the sol- (V), m.p. 223-224". The reaction mixture had a strong odor of vent a small amount of white solid. This solid was recrystallized mesitol, but no attempt was made to isolate it. twive from hexane to yield white needles of a-t-butoxy-a-mesityl- 2-Mesity1-lj3-indandionewith Diphenyliodonium Chloride .- acetophenone-0-carboxylic acid, m.p. llE~116~. To a solution of 84.8 mg. (0.76 mmole) of potassium t-butoxide in Anal. Calcd. for CZZHZ~~O~:C, 74.55; H, 7.39; mol. wt., 20 ml. of t-butyl alcohol there was added with stirring 200 mg. 354.43. Found: C, 74.50; H, 7.36; mol. wt., 392 and 311. (0.76 mmole) of l' and 243 mg. (0.76 mmole) of diphenyliodo- Removal of the &Butyl Group in Compound VI.-A solution of nium chloride. The orange solution was refluxed overnight, dur- 250 mg. of VI in 15 ml. of dioxane and 5 ml. of 6 N hydrochloric ing which time it turned a light yellow, and all the iodonium cation acid was heated on a steam bath for 2 hr. During this time the was consumed. The solvent was removed, and the residue was solution was reduced to half the volume, with formation of light chromatographed on a 100-g. Florid column. The ether eluate ivory colored needles. The mixture was diluted with 25 ml. of yielded a yellow oil which after two distillations at 180-200' water, the solid was collected and chromatographed on silica gel.
    [Show full text]
  • Inorganic Chemistry for Dummies® Published by John Wiley & Sons, Inc
    Inorganic Chemistry Inorganic Chemistry by Michael L. Matson and Alvin W. Orbaek Inorganic Chemistry For Dummies® Published by John Wiley & Sons, Inc. 111 River St. Hoboken, NJ 07030-5774 www.wiley.com Copyright © 2013 by John Wiley & Sons, Inc., Hoboken, New Jersey Published by John Wiley & Sons, Inc., Hoboken, New Jersey Published simultaneously in Canada No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except as permitted under Sections 107 or 108 of the 1976 United States Copyright Act, without either the prior written permis- sion of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 646-8600. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http://www.wiley. com/go/permissions. Trademarks: Wiley, the Wiley logo, For Dummies, the Dummies Man logo, A Reference for the Rest of Us!, The Dummies Way, Dummies Daily, The Fun and Easy Way, Dummies.com, Making Everything Easier, and related trade dress are trademarks or registered trademarks of John Wiley & Sons, Inc. and/or its affiliates in the United States and other countries, and may not be used without written permission. All other trade- marks are the property of their respective owners. John Wiley & Sons, Inc., is not associated with any product or vendor mentioned in this book.
    [Show full text]
  • 76 Chapt-24-Organic2
    The Chemistry of Alkanes Physical Properties of Alkanes as molecular size increases so does the boiling point of the alkane increased size increased dispersion forces Alkanes Boiling Point ˚C H Methane CH 4 H C H -161.6 H H H Ethane C2H6 H C C H -88.6 H H Propane C3H8 CH3 (CH2)1 CH3 -42.1 Butane C4H10 CH3 (CH2)2 CH3 -0.5 Pentane C5H12 CH3 (CH2)3 CH3 36.1 hexane C6H14 CH3 (CH2)4 CH3 68.7 Chemical Reactions and Alkanes because the C-C and C-H bonds are relatively strong , the alkanes are fairly unreactive their inertness makes them valuable as lubricating materials and as backbone material in the construction of other hydrocarbons Combustion of Alkanes At high temperatures alkanes combust ΔH˚ CH4 + O2 CO2 + 2H2O -890.4 kJ C4H10 + 13/2O2 4CO2 + 5H2O -3119 kJ these reactions are all highly exothermic Halogenation of Alkanes at temperatures above 100 ˚C CH4 + Cl2 CH3Cl + HCl chloromethane CH3Cl + Cl2 CH2Cl2 + HCl dichloromethane CH2Cl2 + Cl2 CHCl3 + HCl trichloromethane chloroform CHCl3 + Cl2 CCl4 + HCl tetrachloromethane Carbon tetrachloride Mechanism for Halogenation of Methane CH4 + Cl2 CH3Cl + HCl hν Cl2 • Cl + • Cl hν: energy required to break the Cl-Cl bond • Cl H H C H H • Cl is very reactive and able to attack the C-H bond Mechanism for Halogenation of Methane CH4 + Cl2 CH3Cl + HCl CH4 + • Cl • CH3 + HCl H Cl H • C H H Mechanism for Halogenation of Methane CH4 + Cl2 CH3Cl + HCl • CH3 + Cl2 CH3 Cl + • Cl Cl Cl H • Cl • C H H H Cl C H H Mechanism for Halogenation of Methane Cl2 • Cl + • Cl chlorine free radical CH4 + • Cl • CH3 + HCl
    [Show full text]
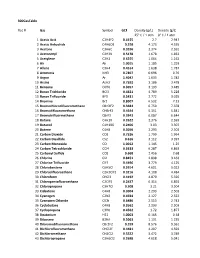
  • Gas Conversion Factor for 300 Series
    300GasTable Rec # Gas Symbol GCF Density (g/L) Density (g/L) 25° C / 1 atm 0° C / 1 atm 1 Acetic Acid C2H4F2 0.4155 2.7 2.947 2 Acetic Anhydride C4H6O3 0.258 4.173 4.555 3 Acetone C3H6O 0.3556 2.374 2.591 4 Acetonitryl C2H3N 0.5178 1.678 1.832 5 Acetylene C2H2 0.6255 1.064 1.162 6 Air Air 1.0015 1.185 1.293 7 Allene C3H4 0.4514 1.638 1.787 8 Ammonia NH3 0.7807 0.696 0.76 9 Argon Ar 1.4047 1.633 1.782 10 Arsine AsH3 0.7592 3.186 3.478 11 Benzene C6H6 0.3057 3.193 3.485 12 Boron Trichloride BCl3 0.4421 4.789 5.228 13 Boron Triflouride BF3 0.5431 2.772 3.025 14 Bromine Br2 0.8007 6.532 7.13 15 Bromochlorodifluoromethane CBrClF2 0.3684 6.759 7.378 16 Bromodifluoromethane CHBrF2 0.4644 5.351 5.841 17 Bromotrifluormethane CBrF3 0.3943 6.087 6.644 18 Butane C4H10 0.2622 2.376 2.593 19 Butanol C4H10O 0.2406 3.03 3.307 20 Butene C4H8 0.3056 2.293 2.503 21 Carbon Dioxide CO2 0.7526 1.799 1.964 22 Carbon Disulfide CS2 0.616 3.112 3.397 23 Carbon Monoxide CO 1.0012 1.145 1.25 24 Carbon Tetrachloride CCl4 0.3333 6.287 6.863 25 Carbonyl Sulfide COS 0.668 2.456 2.68 26 Chlorine Cl2 0.8451 2.898 3.163 27 Chlorine Trifluoride ClF3 0.4496 3.779 4.125 28 Chlorobenzene C6H5Cl 0.2614 4.601 5.022 29 Chlorodifluoroethane C2H3ClF2 0.3216 4.108 4.484 30 Chloroform CHCl3 0.4192 4.879 5.326 31 Chloropentafluoroethane C2ClF5 0.2437 6.314 6.892 32 Chloropropane C3H7Cl 0.308 3.21 3.504 33 Cisbutene C4H8 0.3004 2.293 2.503 34 Cyanogen C2N2 0.4924 2.127 2.322 35 Cyanogen Chloride ClCN 0.6486 2.513 2.743 36 Cyclobutane C4H8 0.3562 2.293 2.503 37 Cyclopropane C3H6 0.4562
    [Show full text]
  • Revised Group Additivity Values for Enthalpies of Formation (At 298 K) of Carbon– Hydrogen and Carbon–Hydrogen–Oxygen Compounds
    Revised Group Additivity Values for Enthalpies of Formation (at 298 K) of Carbon– Hydrogen and Carbon–Hydrogen–Oxygen Compounds Cite as: Journal of Physical and Chemical Reference Data 25, 1411 (1996); https://doi.org/10.1063/1.555988 Submitted: 17 January 1996 . Published Online: 15 October 2009 N. Cohen ARTICLES YOU MAY BE INTERESTED IN Additivity Rules for the Estimation of Molecular Properties. Thermodynamic Properties The Journal of Chemical Physics 29, 546 (1958); https://doi.org/10.1063/1.1744539 Critical Evaluation of Thermochemical Properties of C1–C4 Species: Updated Group- Contributions to Estimate Thermochemical Properties Journal of Physical and Chemical Reference Data 44, 013101 (2015); https:// doi.org/10.1063/1.4902535 Estimation of the Thermodynamic Properties of Hydrocarbons at 298.15 K Journal of Physical and Chemical Reference Data 17, 1637 (1988); https:// doi.org/10.1063/1.555814 Journal of Physical and Chemical Reference Data 25, 1411 (1996); https://doi.org/10.1063/1.555988 25, 1411 © 1996 American Institute of Physics for the National Institute of Standards and Technology. Revised Group Additivity Values for Enthalpies of Formation (at 298 K) of Carbon-Hydrogen and Carbon-Hydrogen-Oxygen Compounds N. Cohen Thermochemical Kinetics Research, 6507 SE 31st Avenue, Portland, Oregon 97202-8627 Received January 17, 1996; revised manuscript received September 4, 1996 A program has been undertaken for the evaluation and revision of group additivity values (GAVs) necessary for predicting, by means of Benson's group additivity method, thermochemical properties of organic molecules. This review reports on the portion of that program dealing with GAVs for enthalpies of formation at 298.15 K (hereinafter abbreviated as 298 K) for carbon-hydrogen and carbon-hydrogen-oxygen compounds.
    [Show full text]
  • Standard Thermodynamic Properties of Chemical
    STANDARD THERMODYNAMIC PROPERTIES OF CHEMICAL SUBSTANCES ∆ ° –1 ∆ ° –1 ° –1 –1 –1 –1 Molecular fH /kJ mol fG /kJ mol S /J mol K Cp/J mol K formula Name Crys. Liq. Gas Crys. Liq. Gas Crys. Liq. Gas Crys. Liq. Gas Ac Actinium 0.0 406.0 366.0 56.5 188.1 27.2 20.8 Ag Silver 0.0 284.9 246.0 42.6 173.0 25.4 20.8 AgBr Silver(I) bromide -100.4 -96.9 107.1 52.4 AgBrO3 Silver(I) bromate -10.5 71.3 151.9 AgCl Silver(I) chloride -127.0 -109.8 96.3 50.8 AgClO3 Silver(I) chlorate -30.3 64.5 142.0 AgClO4 Silver(I) perchlorate -31.1 AgF Silver(I) fluoride -204.6 AgF2 Silver(II) fluoride -360.0 AgI Silver(I) iodide -61.8 -66.2 115.5 56.8 AgIO3 Silver(I) iodate -171.1 -93.7 149.4 102.9 AgNO3 Silver(I) nitrate -124.4 -33.4 140.9 93.1 Ag2 Disilver 410.0 358.8 257.1 37.0 Ag2CrO4 Silver(I) chromate -731.7 -641.8 217.6 142.3 Ag2O Silver(I) oxide -31.1 -11.2 121.3 65.9 Ag2O2 Silver(II) oxide -24.3 27.6 117.0 88.0 Ag2O3 Silver(III) oxide 33.9 121.4 100.0 Ag2O4S Silver(I) sulfate -715.9 -618.4 200.4 131.4 Ag2S Silver(I) sulfide (argentite) -32.6 -40.7 144.0 76.5 Al Aluminum 0.0 330.0 289.4 28.3 164.6 24.4 21.4 AlB3H12 Aluminum borohydride -16.3 13.0 145.0 147.0 289.1 379.2 194.6 AlBr Aluminum monobromide -4.0 -42.0 239.5 35.6 AlBr3 Aluminum tribromide -527.2 -425.1 180.2 100.6 AlCl Aluminum monochloride -47.7 -74.1 228.1 35.0 AlCl2 Aluminum dichloride -331.0 AlCl3 Aluminum trichloride -704.2 -583.2 -628.8 109.3 91.1 AlF Aluminum monofluoride -258.2 -283.7 215.0 31.9 AlF3 Aluminum trifluoride -1510.4 -1204.6 -1431.1 -1188.2 66.5 277.1 75.1 62.6 AlF4Na Sodium tetrafluoroaluminate
    [Show full text]
  • Water Feed Methods to Control Mw Distribution and Byproducts of the Carbamylation of Urea
    (19) TZZ _T (11) EP 2 949 687 A1 (12) EUROPEAN PATENT APPLICATION (43) Date of publication: (51) Int Cl.: 02.12.2015 Bulletin 2015/49 C08G 71/02 (2006.01) C08G 63/48 (2006.01) (21) Application number: 15167165.8 (22) Date of filing: 11.05.2015 (84) Designated Contracting States: (72) Inventors: AL AT BE BG CH CY CZ DE DK EE ES FI FR GB • Anderson, Jeff R. GR HR HU IE IS IT LI LT LU LV MC MK MT NL NO Midland, Michigan 48642 (US) PL PT RO RS SE SI SK SM TR • Daryoosh, Beigzadeh Designated Extension States: Midland, Michigan 48640 (US) BA ME • Yiyong, He Designated Validation States: Midland, Michigan 48642 (US) MA • Congcong, Lu Midland, Michigan 48640 (US) (30) Priority: 29.05.2014 US 201462004545 P (74) Representative: Houghton, Mark Phillip (71) Applicant: Dow Global Technologies Llc Patent Outsourcing Limited Midland, MI 48674 (US) 1 King Street Bakewell, Derbyshire DE45 1DZ (GB) (54) WATER FEED METHODS TO CONTROL MW DISTRIBUTION AND BYPRODUCTS OF THE CARBAMYLATION OF UREA (57) The present invention provides methods for carbamylation catalysts. The polycarbamate of the making a polycarbamate by feeding a) a urea in fluid form present invention when combined with a polyaldehyde into areaction medium containing b)an alkyd polyol, such or an acetal or hemiacetal thereof as a second compo- as a short or med oil alkyd polyol to form a reaction mix- nent makes a multicomponent composition that is sub- ture and then carbamylating the alkyd polyol by heating stantially isocyanate-free, and cures at a temperature of the reaction mixture while feeding water in to the reaction from 0 °C to less than 80 °C to form a crosslinked poly- mixture, preferably, in the presence of one or more c) urethane.
    [Show full text]
  • (12) United States Patent (10) Patent No.: US 8,911,640 B2 Nappa Et Al
    USOO891. 1640B2 (12) United States Patent (10) Patent No.: US 8,911,640 B2 Nappa et al. (45) Date of Patent: Dec. 16, 2014 (54) COMPOSITIONS COMPRISING 5,736,063 A 4/1998 Richard et al. FLUOROOLEFNS AND USES THEREOF 5,744,052 A 4/1998 Bivens 5,788,886 A 8, 1998 Minor et al. 5,897.299 A * 4/1999 Fukunaga ..................... 417.316 (71) Applicant: E I du Pont de Nemours and 5,969,198 A 10/1999 Thenappan et al. Company, Wilmington, DE (US) 6,053,008 A 4/2000 Arman et al. 6,065.305 A 5/2000 Arman et al. (72) Inventors: Mario Joseph Nappa, Newark, DE 6,076,372 A 6/2000 Acharya et al. 6,111,150 A 8/2000 Sakyu et al. (US); Barbara Haviland Minor, Elkton, 6,176,102 B1 1/2001 Novak et al. MD (US); Allen Capron Sievert, 6,258,292 B1 7/2001 Turner Elkton, MD (US) 6,300,378 B1 10/2001 Tapscott 6.426,019 B1 7/2002 Acharya et al. (73) Assignee: E I du Pont de Nemours and 6,610,250 B1 8, 2003 Tuma Company, Wilmington, DE (US) 6,858,571 B2 2/2005 Pham et al. 6,969,701 B2 11/2005 Singh et al. 7,708,903 B2 5, 2010 Sievert et al. *) Notice: Subject to anyy disclaimer, the term of this 8,012,368 B2 9/2011 Nappa et al. patent is extended or adjusted under 35 8,070,976 B2 12/2011 Nappa et al. U.S.C. 154(b) by 0 days.
    [Show full text]
  • 5.157 TABLE 5.29 Van Der Waals' Constants for Gases the Van Der
    DEAN #37261 (McGHP) RIGHT INTERACTIVE top of rh PHYSICAL PROPERTIES 5.157 base of rh cap height TABLE 5.29 Van der Waals’ Constants for Gases base of text The van der Waals’ equation of state for a real gas is: na2 ͩͪP ϩ (V Ϫ nb) ϭ nRT for n moles V2 where P is the pressure, V the volume (in liters per mole ϭ 0.001 m3 per mole in the SI system), T the temperature (in degrees Kelvin), n the amount of substance (in moles), and R the gas constant. To use the values of a and b in the table, P must be expressed in the same units as in the gas constant. Thus, the pressure of a standard atmosphere may be expressed in the SI system as follows: 1 atm ϭ 101,325 N · mϪ2 ϭ 101,325 Pa ϭ 1.01325 bar The appropriate value for the gas constant is: 0.083 144 1 L · bar · KϪ1 · molϪ1 or 0.082 056 L · atm · KϪ1 · molϪ1 The van der Waals’ constants are related to the critical temperature and pressure, tc and Pc, in Table 6.5 by: 27 RT22 RT a ϭ ccand b ϭ 64 Pcc8 P Substance a,L2 · bar · molϪ2 b,L·molϪ1 Acetaldehyde 11.37 0.08695 Acetic acid 17.71 0.1065 Acetic anhydride 26.8 0.157 Acetone 16.02 0.1124 Acetonitrile 17.89 0.1169 Acetyl chloride 12.80 0.08979 Acetylene 4.516 0.05218 Acrylic acid 19.45 0.1127 Acrylonitrile 18.37 0.1222 Allene 8.235 0.07467 Allyl alcohol 15.17 0.1036 Aluminum trichloride 42.63 0.2450 2-Aminoethanol 7.616 0.0431 Ammonia 4.225 0.03713 Ammonium chloride 2.380 0.00734 Aniline 29.14 0.1486 Antimony tribromide 42.08 0.1658 Argon 1.355 0.03201 Arsenic trichloride 17.23 0.1039 Arsine 6.327 0.06048 Benzaldehyde 30.30 0.1553 Benzene 18.82
    [Show full text]
  • (12) United States Patent (10) Patent No.: US 6,596,206 B2 Lee (45) Date of Patent: *Jul
    USOO6596206B2 (12) United States Patent (10) Patent No.: US 6,596,206 B2 Lee (45) Date of Patent: *Jul. 22, 2003 (54) GENERATION OF PHARMACEUTICAL FOREIGN PATENT DOCUMENTS AENESSING FOCUSED WO WO OO/37169O542314 6/20007/1998 (75) Inventor: partson-Hui Lee, Mountain View, W W s: 2: OTHER PUBLICATIONS (73) Assignee: Picoliter Inc., Sunnyvale, CA (US) Debenedetti et al. (1993), “Application of Supercritical Fluids for the Production of Sustained Delivery Devices.” (*) Notice: Subject to any disclaimer, the term of this Journal of Controlled Release 24:27–44. patent is extended or adjusted under 35 Tom et al. (1991), “Formation of Bioerodible Polymeric U.S.C. 154(b) by 14 days. Microspheres and Microparticles by Rapid Expansion of Supercritical Solutions,” Biotechnol. Prog. 7(5):403-411. This patent is Subject to a terminal dis- Chattopadhyay et al. (2001), “Production of Griseofulvin claimer. Nanoparticles Using Supercritical CO2 Antisolvent with Enhanced Mass Transfer.” International Journal of Phar (21) Appl. No.: 09/823,899 maceutics 228:19-31. (22) Filed: Mar 30, 2001 Jung et al. (2001), “Particle Design Using Supercritical e a Vs Fluids: Literature and Patent Survey,” Journal of Supercriti (65) Prior Publication Data cal Fluids 20:179-219. Primary Examiner Mary Lynn Theisen US 2002/0142049 A1 Oct. 3, 2002 (74) Attorney, Agent, or Firm-Dianne E. Reed; Reed & (51) Int. Cl." .................................................. B29C 9/00 Eberle LLP (52) U.S. Cl. ....................... 264/9; 264/5; 2647. (57) ABSTRACT (58) Field of Search ......................... 264/9, 7, 5; 425/6, A method and device for generating pharmaceutical agent 425/10 particles using focused acoustic energy are provided.
    [Show full text]