Aryabhatiya with English Commentary
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
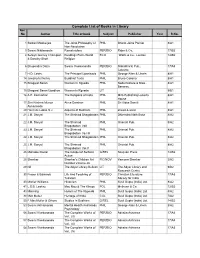
Complete List of Books in Library Acc No Author Title of Book Subject Publisher Year R.No
Complete List of Books in Library Acc No Author Title of book Subject Publisher Year R.No. 1 Satkari Mookerjee The Jaina Philosophy of PHIL Bharat Jaina Parisat 8/A1 Non-Absolutism 3 Swami Nikilananda Ramakrishna PER/BIO Rider & Co. 17/B2 4 Selwyn Gurney Champion Readings From World ECO `Watts & Co., London 14/B2 & Dorothy Short Religion 6 Bhupendra Datta Swami Vivekananda PER/BIO Nababharat Pub., 17/A3 Calcutta 7 H.D. Lewis The Principal Upanisads PHIL George Allen & Unwin 8/A1 14 Jawaherlal Nehru Buddhist Texts PHIL Bruno Cassirer 8/A1 15 Bhagwat Saran Women In Rgveda PHIL Nada Kishore & Bros., 8/A1 Benares. 15 Bhagwat Saran Upadhya Women in Rgveda LIT 9/B1 16 A.P. Karmarkar The Religions of India PHIL Mira Publishing Lonavla 8/A1 House 17 Shri Krishna Menon Atma-Darshan PHIL Sri Vidya Samiti 8/A1 Atmananda 20 Henri de Lubac S.J. Aspects of Budhism PHIL sheed & ward 8/A1 21 J.M. Sanyal The Shrimad Bhagabatam PHIL Dhirendra Nath Bose 8/A2 22 J.M. Sanyal The Shrimad PHIL Oriental Pub. 8/A2 Bhagabatam VolI 23 J.M. Sanyal The Shrimad PHIL Oriental Pub. 8/A2 Bhagabatam Vo.l III 24 J.M. Sanyal The Shrimad Bhagabatam PHIL Oriental Pub. 8/A2 25 J.M. Sanyal The Shrimad PHIL Oriental Pub. 8/A2 Bhagabatam Vol.V 26 Mahadev Desai The Gospel of Selfless G/REL Navijvan Press 14/B2 Action 28 Shankar Shankar's Children Art FIC/NOV Yamuna Shankar 2/A2 Number Volume 28 29 Nil The Adyar Library Bulletin LIT The Adyar Library and 9/B2 Research Centre 30 Fraser & Edwards Life And Teaching of PER/BIO Christian Literature 17/A3 Tukaram Society for India 40 Monier Williams Hinduism PHIL Susil Gupta (India) Ltd. -

Mathematics INSA, New Delhi CLASS NO
Mathematics INSA, New Delhi CLASS NO. WISE CHECK LIST Page : 1 ------------------------- Date : 5/06/2012 ------------------------------------------------------------------------- Accn No. T i t l e / A u t h o r Copies ------------------------------------------------------------------------- 18748 Physicalism in mathematics / Irvine, A.D. 340. 1 : Kluwer Academic, 1990 51.001.1 IRV 16606 Wittgenstein's philosophy of mathematics / Klenk, V.H. 1 : Martinus Nijhoff, 1976 51.001.1 KLE 18031 Mathematics in philosophy : Selected essay / Parsons, 1 Charles. : Cornell University Press, 1983 51.001.1 PAR HS 2259 Introduction to mathematical philosophy / Russell, Bertrand. : George Allen & Unwin, 1975 51.001.1 RUS 17664 Nature mathematized : Historical and philosophical 1 case studies in classical modern natural philosophy : Proceedings / Shea, William R. 340. : D. Reidel 51.001.1 SHE 18910 Mathematical intuition: phenomenology and mathematical 1 knowledge / Tieszen, Richard L. : Kluwer Academic Publishing, 1989 51.001.1 TIE 15502 Remarks on the foundations of mathematics 1 / Wittgenstein, Ludwig. : Basil Black Will, 1967 51.001.1 WIT 5607 Foundations of mathematics : Study in the philosophy 1 of science / Beth, Evert W. : North-Holland Publishing , 1959 51.001.3:16 BET 16621 Developing mathematics in third world countries : 1 Proceedings / Elton, M.E.A. 340. : North-Holland, 1979 51.001.6(061.3) ELT 15888 Optimal control theory / Berkovitz, L.D. : Springer- 1 Verlag, 1974 51:007 BER file:///C|/Documents%20and%20Settings/Abhishek%20Sinha/Desktop/Mathematics.txt[7/20/2012 5:09:31 PM] 29 Mathematics as a cultural clue : And other essays 1 / Keyser, Cassius Jackson. : Yeshiva University, 1947 51:008 KEY 9914 Foundations of mathematical logic / Curry, Haskell B. -

Book of Abstracts
IIT Gandhinagar, 16-17 March 2013 Workshop on Promoting History of Science in India ABSTRACTS Prof. Roddam Narasimha Barbarous Algebra, Inferred Axioms: Eastern Modes in the Rise of Western Science A proper assessment of classical Indic science demands greater understanding of the roots of the European scientific miracle that occurred between the late 16th and early 18th centuries. It is here proposed that, in the exact sciences, this European miracle can be traced to the advent of ‘barbarous’ (i.e. foreign) algebra, as Descartes called it, and to a new epistemology based on ‘inferred’ axioms as advocated by Francis Bacon and brilliantly implemented by Isaac Newton. Both of these developments can be seen as representing a calculated European departure from Hellenist philosophies, accompanied by a creative Europeanization of Indic modes of scientific thinking. Prof. Roddam Narasimha, an eminent scientist and the chairman of Engineering Mechanics Unit at the Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore, has made contributions to the epistemology of Indian science. He was awarded Padma Vishushan this year. Email: [email protected] Prof. R.N. Iyengar Astronomy in Vedic Times: Indian Astronomy before the Common Era Astronomy popularly means knowledge about stars, planets, sun, moon, eclipses, comets and the recent news makers namely, asteroids and meteorites. Ancient people certainly knew something about all of the above though not in the same form or detail as we know now. The question remains what did they know and when. To a large extent for the Siddhāntic period (roughly starting with the Common Era CE) the above questions have been well investigated. -

Mathematicians
MATHEMATICIANS [MATHEMATICIANS] Authors: Oliver Knill: 2000 Literature: Started from a list of names with birthdates grabbed from mactutor in 2000. Abbe [Abbe] Abbe Ernst (1840-1909) Abel [Abel] Abel Niels Henrik (1802-1829) Norwegian mathematician. Significant contributions to algebra and anal- ysis, in particular the study of groups and series. Famous for proving the insolubility of the quintic equation at the age of 19. AbrahamMax [AbrahamMax] Abraham Max (1875-1922) Ackermann [Ackermann] Ackermann Wilhelm (1896-1962) AdamsFrank [AdamsFrank] Adams J Frank (1930-1989) Adams [Adams] Adams John Couch (1819-1892) Adelard [Adelard] Adelard of Bath (1075-1160) Adler [Adler] Adler August (1863-1923) Adrain [Adrain] Adrain Robert (1775-1843) Aepinus [Aepinus] Aepinus Franz (1724-1802) Agnesi [Agnesi] Agnesi Maria (1718-1799) Ahlfors [Ahlfors] Ahlfors Lars (1907-1996) Finnish mathematician working in complex analysis, was also professor at Harvard from 1946, retiring in 1977. Ahlfors won both the Fields medal in 1936 and the Wolf prize in 1981. Ahmes [Ahmes] Ahmes (1680BC-1620BC) Aida [Aida] Aida Yasuaki (1747-1817) Aiken [Aiken] Aiken Howard (1900-1973) Airy [Airy] Airy George (1801-1892) Aitken [Aitken] Aitken Alec (1895-1967) Ajima [Ajima] Ajima Naonobu (1732-1798) Akhiezer [Akhiezer] Akhiezer Naum Ilich (1901-1980) Albanese [Albanese] Albanese Giacomo (1890-1948) Albert [Albert] Albert of Saxony (1316-1390) AlbertAbraham [AlbertAbraham] Albert A Adrian (1905-1972) Alberti [Alberti] Alberti Leone (1404-1472) Albertus [Albertus] Albertus Magnus -

Aryabha~A and Axial Rotation of Earth 2
GENERAL I ARTICLE Aryabha~a and Axial Rotation of Earth 2. Naksatra Dina (The Sidereal Day) Amartya Kumar Dutta In the first part of this series, we discussed the celestial sphere and .Aryabhata's principle of ax ial rotation; in this part we shall discuss in de tail the concept of sidereal day and then men tion .Aryabhata's computations on the duration of sidereal day. Amartya Kumar Dutta is in the Stat-Math Unit of It. is unfortunate that science students in India, by and Indian Statisticallnstiutte, large, do not have technical awareness regarding the re Kolkata. His research searches of ancient Indian scientists. Thus, although interest is in commutative there are plenty of articles on Aryabhata, their contents algebra. have remained confined to research journals and schol arly texts without percolating into the general cultural Part 1. Aryabhata and Axial Ro consciousness. tation of Earth - Khagola (The Celestial Spherel. Resonance, The original statements of Aryabhata on axial rot.at.ion Vol.ll, No.3, pp.51-68, 2006. and sidereal day are spread over 4 verses out of his 85 verses on astronomy. It. will not be possible to make a se rious analysis of the entire range of Aryabhat.a's work in a few pages. We hope that the preliminary exposure will encourage youngsters to acquire some general know ledge of astronomy and make a deeper study of A.ryabhata's work using existing literatures and their own indepen dent judgements. Rising and Setting of Stars Recall that, due to rotation of the Earth, the so-called fixed stars appear to execute a daily revolut.ion around t.he Earth. -

Ancient Indian Leaps Into Mathematics Editors B.S
B.S. Yadav Man Mohan Editors Ancient Indian Leaps into Mathematics Editors B.S. Yadav (Deceased) Man Mohan Ramjas College University of Delhi 110 007 New Delhi India [email protected] ISBN 978-0-8176-4694-3 e-ISBN 978-0-8176-4695-0 DOI 10.1007/978-0-8176-4695-0 Springer New York Dordrecht Heidelberg London Library of Congress Control Number: 2010937771 Mathematics Subject Classification (2010): 01A32, 01A16, 01A17, 01A25, 01A27, 01A29 c Springer Science+Business Media, LLC 2011 All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. Printed on acid-free paper www.birkhauser-science.com Dedicated to the memory of U. N. SINGH The Founder of the Indian Society for History of Mathematics U. N. Singh (November 19, 1920 – April 9, 1989) Professor B. S. Yadav (31 July 1931 – 24 February 2010) B. S. Yadav was born in Mathura, India. He dedicated his whole life to the cause of mathematics and the history of mathematical sciences. -

Kamala¯Kara Commentary on the Work, Called Tattvavivekodāharan
K related to the Siddhānta-Tattvaviveka, one a regular Kamala¯kara commentary on the work, called Tattvavivekodāharan. a, and the other a supplement to that work, called Śes.āvasanā, in which he supplied elucidations and new K. V. SARMA material for a proper understanding of his main work. He held the Sūryasiddhānta in great esteem and also wrote a Kamalākara was one of the most erudite and forward- commentary on that work. looking Indian astronomers who flourished in Varanasi Kamalākara was a critic of Bhāskara and his during the seventeenth century. Belonging to Mahar- Siddhāntaśiroman. i, and an arch-rival of Munīśvara, a ashtrian stock, and born in about 1610, Kamalākara close follower of Bhāskara. This rivalry erupted into came from a long unbroken line of astronomers, bitter critiques on the astronomical front. Thus Ranga- originally settled at the village of Godā on the northern nātha, younger brother of Kamalākara, wrote, at the . banks of the river Godāvarī. Towards AD 1500, the insistence of the latter, a critique on Munīśvara’s Bhangī family migrated to Varanasi and came to be regarded as method (winding method) of true planets, entitled . reputed astronomers and astrologers. Kamalākara Bhangī-vibhangī (Defacement of the Bhangi), to which . studied traditional Hindu astronomy under his elder Munīśvara replied with a Khand.ana (Counter). Munīś- brother Divākara, but extended the range of his studies vara attacked the theory of precession advocated by to Islamic astronomy, particularly to the school of Kamalākara, and Ranganātha refuted the criticisms of his Ulugh Beg of Samarkand. He also studied Greek brother in his Loha-gola-khan. -

A Study on the Encoding Systems in Vedic Era and Modern Era 1K
International Journal of Pure and Applied Mathematics Volume 114 No. 7 2017, 425-433 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu Special Issue ijpam.eu A Study on the Encoding Systems in Vedic Era and Modern Era 1K. Lakshmi Priya and 2R. Parameswaran 1Department of Mathematics, School of Arts and Sciences, Amrita University, Kochi. [email protected] 2Department of Mathematics, School of Arts and Sciences, Amrita University, Kochi. [email protected] Abstract Encoding is the action of transferring a message in to codes. In this paper I present a study on the encoding systems in vedic era and modern era. The Sanskrit verses written in the vedic era are not just the praises of the Gods they are also numerical codes. In ancient India there were three means of recording numerals in Sanskrit words which are Katapayadi system, Bhutasamkhya system and Aryabhata numeration. These systems were used by many ancient mathematicians in India. In this paper the Katapayadi system used in vedic times is applied to modern ciphers– Vigenere Cipher and Affine Cipher. Key Words:Katapayadi system, vigenere cipher, affine cipher. 425 International Journal of Pure and Applied Mathematics Special Issue 1. Introduction Encoding is the process of transforming messages into an arrangement required for data transmission, storage and compression/decompression. In cryptography, encryption is the method of transforming information using an algorithm to make it illegible to anyone except those owning special information, usually called as a key. In vedic era, Sanskrit is the language used. It is supposed to be the ancient language, from which most of the modern dialects are developed. -

Astronomy in India
TRADITIONSKnowledg & PRACTICES OF INDIA e Textbook for Class XI Module 1 Astronomy in India CENTRAL BOARD OF SECONDARY EDUCATION Shiksha Kendra, 2, Community Centre, Preet Vihar, Delhi-110 092 India TRADITIONSKnowledg & PRACTICESe OF INDIA Textbook for Class XI Module 1 Astronomy in India CENTRAL BOARD OF SECONDARY EDUCATION Shiksha Kendra, 2, Community Centre, Preet Vihar, Delhi-110 092 India No part of this publication may be reproduced or stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical photocopying, recording or otherwise, without the prior permission of the Central Board of Secondary Education (CBSE). Preface India has a rich tradition of intellectual inquiry and a textual heritage that goes back to several hundreds of years. India was magnificently advanced in knowledge traditions and practices during the ancient and medieval times. The intellectual achievements of Indian thought are found across several fields of study in ancient Indian texts ranging from the Vedas and the Upanishads to a whole range of scriptural, philosophical, scientific, technical and artistic sources. As knowledge of India's traditions and practices has become restricted to a few erudite scholars who have worked in isolation, CBSE seeks to introduce a course in which an effort is made to make it common knowledge once again. Moreover, during its academic interactions and debates at key meetings with scholars and experts, it was decided that CBSE may introduce a course titled ‘Knowledge Traditions and Practices of India’ as a new Elective for classes XI - XII from the year 2012-13. It has been felt that there are many advantages of introducing such a course in our education system. -

Aryabhatta Date an Analytical Study
ARYABHATTA’S DATE AN ANALYTICAL STUDY Dr. M.L. Raja, M.B., B.S., D.O., AVINASH English ARYABHATTA’S DATE AN ANALYTICAL STUDY By- Dr. M.L. Raja Published by AVINASH Printed at Sankav Offset Printerss, Erode Cover Design & Type setting A.P. Nallashivam Published in January 2016 Yugabdom 5117 IPrice `160. ISBN: 978-93-84582-54-8BN: 978i AVINASH Academy on Vibrant National Arts & Scientific Heritage Erode, Tamilnadu Ph : 94433 70129 E-mail : [email protected] PREFACE In the history our Nation, we can find thousands and thousands of great scholars and their works, in almost all fields of science. We can cite examples, at least a few hundred in each century, scattering over a very long period of time, exceeding a minimum of ten thousand years. Their works in the various fields of science are remarkably outstanding, highly astonishing and fully scientific with thorough and clear knowledge, exceeding the modern scientific achievements, at least in a few aspects. But, the most unfortunate thing is, we are very much ignorant of our ancestor’s glorious antiquity, Himalayan achievements, high technological skill and the vast knowledge and wisdom and their highly admirable scientific works are not at all included in our Nation’s educational curriculum. So, it is right time or even if late, it is better late than never, to bring forth these ancient scientific works of our glorious Nation, in the day-light, amongst the present and the future generations of our Nation. With that motive in mind, this book on Âryabhaa is a very small, but a firm step in that direction, where the actual date and name of Âryabhaa and his texts are detailed. -

Review of Research Impact Factor : 5.7631(Uif) Ugc Approved Journal No
Review Of ReseaRch impact factOR : 5.7631(Uif) UGc appROved JOURnal nO. 48514 issn: 2249-894X vOlUme - 8 | issUe - 2 | nOvembeR - 2018 __________________________________________________________________________________________________________________________ ANCIENT INDIAN CONTRIBUTIONS TOWARDS MATHEMATICS Madhuri N. Gadsing Department of Mathematics, Jawahar Arts, Science and Commerce College, Anadur (M.S.), India. ABSTRACT Mathematics having been a progressive science has played a significant role in the development of Indian culture for millennium. In ancient India, the most famous Indian mathematicians, Panini (400 CE), Aryabhata I (500 CE), Brahmagupta (700 CE), Bhaskara I (900 CE), Mahaviracharya (900 CE), Aryabhata II (1000 CE), Bhaskara II (1200 CE), chanced to discover and develop various concepts like, square and square roots, cube and cube roots, zero with place value, combination of fractions, astronomical problems and computations, differential and integral calculus etc., while meditating upon various aspects of arithmetic, geometry, astronomy, modern algebra, etc. In this paper, we review the contribution of Indian mathematicians from ancient times. KEYWORDS: Mathematics , development of Indian , astronomical problems and computations. INTRODUCTION: Mathematics having been a progressive science has played a significant role in the development of Indian culture for millennium. Mathematical ideas that originated in the Indian subcontinent have had a profound impact on the world. The aim of this article is to give a brief review of a few of the outstanding innovations introduced by Indian mathematicians from ancient times. In ancient India, the most famous Indian mathematicians belong to what is known as the classical era [1-8]. This includes Panini (400 CE), Aryabhata I (500 CE) [9], Brahmagupta (700 CE), Bhaskara I (900 CE) [5, 6], Mahavira (900 CE), Aryabhata II (1000 CE), Bhaskaracharya or Bhaskara II (1200 CE) [10-13]. -

EMINENT INDIAN SCIENTIST VENKATESH BAPUJI KETKAR Author
EMINENT INDIAN SCIENTIST VENKATESH BAPUJI KETKAR EMINENT INDIAN SCIENTIST VENKATESH BAPUJI KETKAR Author Siddhi Nitin Mahajan Edited by Ms. Sangeeta Abhayankar Dr. Arvind C. Ranade Content Coordinator, VVM National Convenor, VVM ©Vijnana Bharati September, 2020 First Edition, September 2020 Published by Vijnana Bharati, Head Quarter, Delhi Author Ms. Siddhi Nitin Mahajan Editorial Team Dr. Arvind C. Ranade National Convenor, VVM Ms. Sangeeta Abhayankar Content Coordinator, VVM All rights reserved. No part of the publication may be reproduced in whole or in part, or stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical photocopying, recording, or otherwise without the written permission of the publisher. For information regarding permission, write to: Vijnana Bharati A-4, First Floor, Gulmohar Park, August Kranti Marg, New Delhi- 110049 Cover & Book Design Ms. Babita Rani CONTENTS From Editor's Desk i-ii Preface iii-iv 1 Introduction 1-3 2 Brief history of Indian Astronomy 4-6 3 The family legacy 7-8 4 Venkatesh Ketkar : Early Life and Career 9-10 5 Ketkar and his Almanac Research 11-15 6 Tilak, Ketkar and Pañcānga 16-17 7 Citrā Nakshatra Paksha and Ketaki Pañcānga 18-20 8 Ketkar’s Prediction about Existence of Pluto 21-22 9 Other Research by Ketkar 23-24 10 Multi-talented Ketkar 25 11 Review of Ketkar’s Literature 26-29 12 Some Memories 30-31 13 Final Journey 32-34 References 35 From Editor’s Desk From time antiquity, India possesses a great legacy in Science and Technology which needs to be communicated and informed to the young generation.