DOCSLIB.ORG

Operational Amplifiers: Chapter 3

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Operational Amplifiers: Chapter 3 CHAPTER III LINEAR SYSTEM RESPONSE 3.1 OBJECTIVES The output produced by an operational amplifier (or any other dynamic system) in response to a particular type or class of inputs normally pro­ vides the most important characterization of the system. The purpose of this chapter is to develop the analytic tools necessary to determine the re­ sponse of a system to a specified input. While it is always possible to determine the response of a linear system to a given input exactly, we shall frequently find that greater insight into the design process results when a system response is approximated by the known response of a simpler configuration. For example, when designing a low-level preamplifier intended for audio signals, we might be interested in keeping the frequency response of the amplifier within i 5% of its mid- band value over a particular bandwidth. If it is possible to approximate the amplifier as a two- or three-pole system, the necessary constraints on pole location are relatively straightforward. Similarly, if an oscilloscope vertical amplifier is to be designed, a required specification might be that the over­ shoot of the amplifier output in response to a step input be less than 3 % of its final value. Again, simple constraints result if the system transfer function can be approximated by three or fewer poles. The advantages of approximating the transfer functions of linear systems can only be appreciated with the aid of examples. The LM301A integrated- circuit operational amplifier' has 13 transistors included-in its signal-trans­ mission path. Since each transistor can be modeled as having two capaci­ tors, the transfer function of the amplifier must include 26 poles. Even this estimate is optimistic, since there is distributed capacitance, comparable to transistor capacitances, associated with all of the other components in the signal path. Fortunately, experimental measurements of performance can save us from the conclusion that this amplifier is analytically intractable. Figure 3.la shows the LM301A connected as a unity-gain inverter. Figures 3.1b and 3.lc show the output of this amplifier with the input a -50-mV step 1This amplifier is described in Section 10.4.1. 63 64 Linear System Response 4.7 kn 4.7 k V F -+ V LM301 A 0 - Compensating capacitor (a) 20 mV (b) 2 AsK Figure 3.1 Step responses of inverting amplifier. (a) Connection. (b) Step response with 220-pF compensating capacitor. (c) Step response with 12-pF compensating capacitor. 2 for two different values of compensating capacitor. The responses of an R-C network and an R-L-C network when excited with +50-mV steps supplied from the same generator used to obtain the previous transients are shown in Figs. 3.2a and 3.2b, respectively. The network transfer func­ tions are V0(s) 1 Vi(s) 2.5 X 10- 6 s + I Objectives 65 20 mV (c) 0.5 yAs Figure 3.1-Continued for the response shown in Fig. 3.2a and V0(s) 1 1 Vi(s) 2.5 X 10 4 s2 + 7 X 10- 8s + I for that shown in Fig. 3.2b. We conclude that there are many applications where the first- and second-order transfer functions of Eqns. 3.1 and 3.2 adequately model the closed-loop transfer function of the LM301A when connected and compensated as shown in Fig. 3.1. This same type of modeling process can also be used to approximate the open-loop transfer function of the operational amplifier itself. Assume that the input impedance of the LM301A is large compared to 4.7 ki and that its output impedance is small compared to this value at frequencies of interest. The closed-loop transfer function for the connection shown in Fig. 3.1 is then V0(s) -a(s) Vi(s) 2 + a(s) 2 Compensation is a process by which the response of a system can be modified advan­ tageously, and is described in detail in subsequent sections. 20 mV T (a) 2 S 20 mV (b) 0.5 /s Figure 3.2 Step responses for first- and second-order networks. (a) Step response 6 for V.(s)/Vi(s) = ]/(2.5 X 10- s + 1). (b) Step response for V(s)/Vi(s) = 1/(2.5 X 10 14 S2 + 7 X 10 8s + 1). 66 Laplace Transforms 67 where a(s) is the unloaded open-loop transfer function of the amplifier. Substituting approximate values for closed-loop gain (the negatives of Eqns. 3.1 and 3.2) into Eqn. 3.3 and solving for a(s) yields a~) 8 X 105 a(s) 8X(3.4) and 2.8 X 107 a(s) 2. 0 (3.5) s(3.5 X 10- 7 s + 1) as approximate open-loop gains for the amplifier when compensated with 220-pF and 12-pF capacitors, respectively. We shall see that these approxi­ mate values are quite accurate at frequencies where the magnitude of the loop transmission is near unity. 3.2 LAPLACE TRANSFORMS3 Laplace Transforms offer a method for solving any linear, time-invariant differential equation, and thus can be used to evaluate the response of a linear system to an arbitrary input. Since it is assumed that most readers have had some contact with this subject, and since we do not intend to use this method as our primary analytic tool, the exposure presented here is brief and directed mainly toward introducing notation and definitions that will be used later. 3.2.1 Definitions and Properties The Laplace transform of a time functionf(t) is defined as 2[f(t)] A F(s) A f f(t)e-" dt (3.6) where s is a complex variable o + jw. The inverse Laplace transform of the complex function F(s) is -1[F(s)]A f(t) A F(s)e" ds (3.7) 2.rj ,1-J Fs d A complete discussion is presented in M. F. Gardner and J. L. Barnes, Transientsin LinearSystems, Wiley, New York, 1942. In this section we temporarily suspend the variable and subscript notation used else­ where and conform to tradition by using a lower-case variable to signify a time function and the corresponding capital for its transform. 68 Linear System Response The direct-inverse transform pair is unique4 so that 2-12[ftt)] =f (t (3.8) iff(t) = 0, t < 0, and if f f(t) | e- dt is finite for some real value of a1. A number of theorems useful for the analysis of dynamic systems can be developed from the definitions of the direct and inverse transforms for functions that satisfy the conditions of Eqn. 3.8. The more important of these theorems include the following. 1. Linearity 2[af(t) + bg(t)] = [aF(s) + bG(s)] where a and b are constants. 2. Differentiation Ldf(t) sF(s) - lim f(t) dt =-.0+ (The limit is taken by approaching t = 0 from positive t.) 3. Integration 2 [ f(T) d-] F(s) 4. Convolution 2 [f tf(r)g(t - r) d] = [ ff(t - r)g(r) dr] = F(s)G(s) 5. Time shift 2[f(t - r)] = F(s)e-" if f(t - r) = 0 for (t - r) < 0, where r is a positive constant. 6. Time scale 1 Fs] 2[f(at)] = F -­ a a where a is a positive constant. 7. Initialvalue lim f(t) lim sF(s) t-0+ 8-.co 4 There are three additional constraints called the Direchlet conditions that are satisfied for all signals of physical origin. The interested reader is referred to Gardner and Barnes. Laplace Transforms 69 8. Final value limf (t) = lim sF(s) J-oo 8-0 Theorem 4 is particularly valuable for the analysis of linear systems, since it shows that the Laplace transform of a system output is the prod­ uct of the transform of the input signal and the transform of the impulse response of the system. 3.2.2 Transforms of Common Functions The defining integrals can always be used to convert from a time func­ tion to its transform or vice versa. In practice, tabulated values are fre­ quently used for convenience, and many mathematical or engineering ref­ erencesI contain extensive lists of time functions and corresponding Laplace transforms. A short list of Laplace transforms is presented in Table 3.1. The time functions corresponding to ratios of polynomials in s that are not listed in the table can be evaluated by means of a partialfraction ex­ pansion. The function of interest is written in the form F(s) = p(s) _ p(s) q(s) (s + s1 )(s + s2) . (s + s.) It is assumed that the order of the numerator polynomial is less than that of the denominator. If all of the roots of the denominator polynomial are first order (i.e., s, / si, i # j), F(s) = (3.10) k=1 S + sk where Ak = lim [(s + sk)F(s)] (3.11) k If one or more roots of the denominator polynomial are multiple roots, they contribute terms of the form "ZBk k- BsI~k (3.12) k1(S + Si) k See, for example, A. Erdeyli (Editor) Tables of Integral Transforms, Vol. 1, Bateman Manuscript Project, McGraw-Hill, New York, 1954 and R. E. Boly and G. L. Tuve, (Editors), Handbook of Tables for Applied Engineering Science, The Chemical Rubber Company, Cleveland, 1970. 70 Linear System Response Table 3.1 Laplace Transform Pairs f(t), t > 0 F(s) [f(t) = 0, t < 0] 1 Unit impulse uo(t) 1 Unit step u-1 (t) S2 [f(t) = 1, t > 0] 1 Unit ramp u- 2(t) [f(t) = t, t > 0] 1 tn s+1a n! e-at s + 1 a 1 tn Se-at (s + a)"+1 (n)! 1 1 - e-t/ s(rs + 1 e-a sin wt (s + a)2 + W2 s + a e-a cos Wt (s + a)2 + W22 1 on 2 2 e-t-wn(sin 1 - -2 t), < 1 s /, + 2 s/n + 1 1 - 2 1 2 1 - sin coV/1 - 2 t + tan-' 2, s(s /O,,2 + 2 s/Wn + 1) where m is the order of the multiple root located at s = -si.
Load more

Recommended publications
  • Control Systems
    ECE 380: Control Systems Course Notes: Winter 2014 Prof. Shreyas Sundaram Department of Electrical and Computer Engineering University of Waterloo ii c Shreyas Sundaram Acknowledgments Parts of these course notes are loosely based on lecture notes by Professors Daniel Liberzon, Sean Meyn, and Mark Spong (University of Illinois), on notes by Professors Daniel Davison and Daniel Miller (University of Waterloo), and on parts of the textbook Feedback Control of Dynamic Systems (5th edition) by Franklin, Powell and Emami-Naeini. I claim credit for all typos and mistakes in the notes. The LATEX template for The Not So Short Introduction to LATEX 2" by T. Oetiker et al. was used to typeset portions of these notes. Shreyas Sundaram University of Waterloo c Shreyas Sundaram iv c Shreyas Sundaram Contents 1 Introduction 1 1.1 Dynamical Systems . .1 1.2 What is Control Theory? . .2 1.3 Outline of the Course . .4 2 Review of Complex Numbers 5 3 Review of Laplace Transforms 9 3.1 The Laplace Transform . .9 3.2 The Inverse Laplace Transform . 13 3.2.1 Partial Fraction Expansion . 13 3.3 The Final Value Theorem . 15 4 Linear Time-Invariant Systems 17 4.1 Linearity, Time-Invariance and Causality . 17 4.2 Transfer Functions . 18 4.2.1 Obtaining the transfer function of a differential equation model . 20 4.3 Frequency Response . 21 5 Bode Plots 25 5.1 Rules for Drawing Bode Plots . 26 5.1.1 Bode Plot for Ko ....................... 27 5.1.2 Bode Plot for sq ....................... 28 s −1 s 5.1.3 Bode Plot for ( p + 1) and ( z + 1) .
    [Show full text]
  • Example Problems and Solutions
    EXAMPLE PROBLEMS AND SOLUTIONS A-5-1. In the system of Figure 5-52, x(t) is the input displacement and B(t) is the output angular displacement. Assume that the masses involved are negligibly small and that all motions are restricted to be small; therefore, the system can be considered linear. The initial conditions for x and 0 are zeros, or x(0-) = 0 and H(0-) = 0. Show that this system is a differentiating element. Then obtain the response B(t) when x(t)is a unit-step input. Solution. The equation for the system is b(X - L8) = kLB or The Laplace transform of this last equation, using zero initial conditions, gives And so Thus the system is a differentiating system. For the unit-step input X(s) = l/s,the output O(s)becomes The inverse Laplace transform of O(s)gives Figure 5-52 Mechanical system. Chapter 5 / Transient and Steady-State Response Analyses Figure 5-53 Unit-step input and the response of the mechanical s) stem shown in Figure 5-52. Note that if the value of klb is large the response O(t) approaches a pulse signal as shown in Figure 5-53. A-5-2. Consider the mechanical system shown in Figure 5-54. Suppose that the system is at rest initially [x(o) = 0, i(0) = 01, and at t = 0 it is set into motion by a unit-impulse force. Obtain a mathe- matical model for the system.Then find the motion of the system. Solution. The system is excited by a unit-impulse input.
    [Show full text]
  • Control System Design Methods
    Christiansen-Sec.19.qxd 06:08:2004 6:43 PM Page 19.1 The Electronics Engineers' Handbook, 5th Edition McGraw-Hill, Section 19, pp. 19.1-19.30, 2005. SECTION 19 CONTROL SYSTEMS Control is used to modify the behavior of a system so it behaves in a specific desirable way over time. For example, we may want the speed of a car on the highway to remain as close as possible to 60 miles per hour in spite of possible hills or adverse wind; or we may want an aircraft to follow a desired altitude, heading, and velocity profile independent of wind gusts; or we may want the temperature and pressure in a reactor vessel in a chemical process plant to be maintained at desired levels. All these are being accomplished today by control methods and the above are examples of what automatic control systems are designed to do, without human intervention. Control is used whenever quantities such as speed, altitude, temperature, or voltage must be made to behave in some desirable way over time. This section provides an introduction to control system design methods. P.A., Z.G. In This Section: CHAPTER 19.1 CONTROL SYSTEM DESIGN 19.3 INTRODUCTION 19.3 Proportional-Integral-Derivative Control 19.3 The Role of Control Theory 19.4 MATHEMATICAL DESCRIPTIONS 19.4 Linear Differential Equations 19.4 State Variable Descriptions 19.5 Transfer Functions 19.7 Frequency Response 19.9 ANALYSIS OF DYNAMICAL BEHAVIOR 19.10 System Response, Modes and Stability 19.10 Response of First and Second Order Systems 19.11 Transient Response Performance Specifications for a Second Order
    [Show full text]
  • Non-Integer Order Approximation of a PID-Type Controller for Boost Converters
    energies Article Non-Integer Order Approximation of a PID-Type Controller for Boost Converters Allan G. S. Sánchez 1,* , Francisco J. Pérez-Pinal 2 , Martín A. Rodríguez-Licea 1 and Cornelio Posadas-Castillo 3 1 CONACYT-Instituto Tecnológico de Celaya, Guanajuato 38010, Mexico; [email protected] 2 Instituto Tecnológico de Celaya, Guanajuato 38010, Mexico; [email protected] 3 Facultad de Ingeniería Mecánica y Eléctrica, Universidad Autónoma de Nuevo León, Nuevo León 66455, Mexico; [email protected] * Correspondence: [email protected] Abstract: In this work, the voltage regulation of a boost converter is addressed. A non-integer order PID controller is proposed to deal with the closed-loop instability of the system. The average linear model of the converter is obtained through small-signal approximation. The resulting average linear model is considered divided into minimum and normalized non-minimum phase parts. This approach allows us to design a controller for the minimum phase part of the system, excluding tem- porarily the non-minimum phase one. A fractional-order PID controller approximation is suggested for the minimum phase part of the system. The proposal for the realization of the electrical controller is described and its implementation is used to corroborate its effectiveness when regulating the output voltage in the boost converter. The fractional-order PID approximation achieves regulation of the output voltage in the boost converter by exhibiting the iso-damping property and using a single Citation: Sánchez, A.G.S.; Pérez-Pinal, F.J.; Rodríguez-Licea, control loop, which confirmed its effectiveness in terms of controlling non-minimum phase/variable M.A.; Posadas-Castillo, C.
    [Show full text]
  • Review: Step Response of 1St Order Systems
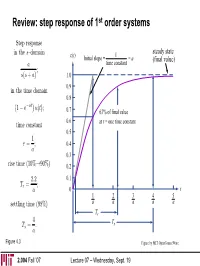
    Review: step response of 1st order systems Step response in the s—domain c(t) 1 steady state Initial slope = = a (final value) a time constant ; s(s + a) 1.0 0.9 in the time domain 0.8 at 1 − e− u(t); 0.7 63% of final value ¡time constant¢ 0.6 at t = one time constant 0.5 1 τ = ; 0.4 a 0.3 rise time (10%→90%) 0.2 2.2 0.1 Tr = ; a 0 t 1 2 3 4 5 settling time (98%) a a a a a Tr 4 T = . Ts s a Figure 4.3 Figure by MIT OpenCourseWare. 2.004 Fall ’07 Lecture 07 – Wednesday, Sept. 19 Review: poles, zeros, and the forced/natural responses jω jω system pole – input pole – system zero – natural response forced response derivative & amplification σ σ −5 0 −5 −2 0 2.004 Fall ’07 Lecture 07 – Wednesday, Sept. 19 Goals for today • Second-order systems response – types of 2nd-order systems • overdamped • underdamped • undamped • critically damped – transient behavior of overdamped 2nd-order systems – transient behavior of underdamped 2nd-order systems – DC motor with non-negligible impedance • Next lecture (Friday): – examples of modeling & transient calculations for electro-mechanical 2nd order systems 2.004 Fall ’07 Lecture 07 – Wednesday, Sept. 19 DC motor system with non-negligible inductance Recall combined equations of motion LsI(s)+RI(s)+KvΩ(s)=Vs(s) ⇒ JsΩ(s)+bΩ(s)=KmI(s) ) LJ Lb KmKv Km s2 + + J s + b + Ω(s)= V (s) R R R R s ⎧ · µ ¶ µ ¶¸ ⎨⎪ (Js + b) Ω(s)=KmI(s) ⎩⎪ Including the DC motor’s inductance, we find Ω(s) Km 1 = Vs(s) LJ b R bR + KmKv ⎧ s2 + + s + Quadratic polynomial denominator ⎪ J L LJ Second—order system ⎪ µ ¶ µ ¶ ⎪ ⎪ ⎪ b ⎪ s + ⎨ I(s) 1 J = µ ¶ ⎪ Vs(s) R b R bR + K K ⎪ 2 m v ⎪ s + + s + ⎪ J L LJ ⎪ µ ¶ µ ¶ ⎪ ⎩⎪ 2.004 Fall ’07 Lecture 07 – Wednesday, Sept.
    [Show full text]
  • Block Diagrams, Feedback and Transient Response Specifications
    Block Diagrams, Feedback and Transient Response Specifications This module introduces the concepts of system block diagrams, feedback control and transient response specifications which are essential concepts for control design and analysis. (This command loads the functions required for computing Laplace and Inverse Laplace transforms. For more information on Laplace transforms, see the Laplace Transforms and Transfer Functions module.) Block Diagrams and Feedback Consider the example of a common household heating system. A household heating system usually consists of a thermostat that measures the room temperature and compares it with an input desired temperature. If the measured temperature is lower than the desired temperature, the thermostat sends a signal that opens the gas valve and starts the combustion in the furnace. The heat from the furnace is then transferred to the rooms of the house which causes the air temperature in the rooms to rise. Once the measured room temperature exceeds the desired temperature by a certain amount, the thermostat turns off the furnace and the cycle repeats. This is an example of a control system and in this case the variable being controlled is the room temperature. This system can be sub-divided into its major parts and represented by the following diagram which shows the directions of information flow. This type of diagram, known as a block diagram, is very useful in understanding how the different components interact and effect the variable of interest. Fig. 1: Block diagram of a household heating system The gas valve, furnace and house can be combined to get one block which can be called the plant of the system.
    [Show full text]
  • Dynamic System Response
    Dynamic System Response • Solution of Linear, Constant-Coefficient, Ordinary Differential Equations – Classical Operator Method – Laplace Transform Method • Laplace Transform Properties • 1st-Order Dynamic System Time and Frequency Response • 2nd-Order Dynamic System Time and Frequency Response Sensors & Actuators in Mechatronics K. Craig Dynamic System Response 1 Laplace Transform Methods • A basic mathematical model used in many areas of engineering is the linear ordinary differential equation with constant coefficients: d nq d n-1q dq a o + a o + +a o + a q = n dt n n-1 dt n-1 L 1 dt 0 o d mq d m-1q dq b i + b i + +b i + b q m dt m m-1 dt m-1 L 1 dt 0 i • qo is the output (response) variable of the system • qi is the input (excitation) variable of the system • an and bm are the physical parameters of the system Sensors & Actuators in Mechatronics K. Craig Dynamic System Response 2 • Straightforward analytical solutions are available no matter how high the order n of the equation. • Review of the classical operator method for solving linear differential equations with constant coefficients will be useful. When the input qi(t) is specified, the right hand side of the equation becomes a known function of time, f(t). • The classical operator method of solution is a three-step procedure: – Find the complimentary (homogeneous) solution qoc for the equation with f(t) = 0. – Find the particular solution qop with f(t) present. – Get the complete solution qo = qoc + qop and evaluate the constants of integration by applying known initial conditions.
    [Show full text]
  • Lecture 7 Amplifier Design 1
    ECE1371 Advanced Analog Circuits Lecture 7 Amplifier Design 1 Trevor Caldwell [email protected] Lecture Plan Date Lecture (Wednesday 2-4pm) Reference Homework 2020-01-07 1 MOD1 & MOD2 PST 2, 3, A 1: Matlab MOD1&2 2020-01-14 2 MODN + Toolbox PST 4, B 2: Toolbox 2020-01-21 3 SC Circuits R 12, CCJM 14 2020-01-28 4 Comparator & Flash ADC CCJM 10 3: Comparator 2020-02-04 5 Example Design 1 PST 7, CCJM 14 2020-02-11 6 Example Design 2 CCJM 18 4: SC MOD2 2020-02-18 Reading Week / ISSCC 2020-02-25 7 Amplifier Design 1 2020-03-03 8 Amplifier Design 2 2020-03-10 9 Noise in SC Circuits 2020-03-17 10 Nyquist-Rate ADCs CCJM 15, 17 Project 2020-03-24 11 Mismatch & MM-Shaping PST 6 2020-03-31 12 Continuous-Time PST 8 2020-04-07 Exam 2020-04-21 Project Presentation (Project Report Due at start of class) 2 ECE1371 Circuit of the Day: Cascode Current Mirror • How do we bias cascode transistors to optimize signal swing? • Standard cascode current mirror wastes too much swing VX = VEFF + VT VY = 2VEFF + 2VT Minimum VZ is 2VEFF + VT, which is VT larger than necessary 3 ECE1371 What you will learn… • Choice of VEFF Several trade-offs with Noise, Bandwidth, Power,… • Amplifier Topology • Amplifier Settling Dominant Pole, Zero and Non-Dominant Pole • Gain-Boosting Stability, Pole-Zero Doublet • Delaying vs. Non-Delaying stages 4 ECE1371 Choice of Effective Voltage • Effective Voltage VEFF = VGS -VT 2IDD 2I VEFF g C W m nox L Assumes square-law model In weak-inversion, this relationship will not hold • What are the trade-offs when choosing an appropriate effective voltage? Noise Power Bandwidth Matching Linearity Swing 5 ECE1371 Thermal Noise and VEFF • Noise Current and Noise Voltage 2 2 4kT IkTgnm 4 Vn gm • Ex.
    [Show full text]
  • Transfer Function Models of Dynamical Processes
    Transfer Function Models of Dynamical Processes Process Dynamics and Control 1 LinearLinear SISOSISO ControlControl SystemsSystems General form of a linear SISO control system: this is a underdetermined higher order differential equation the function must be specified for this ODE to admit a well defined solution 2 TransferTransfer FunctionFunction Heated stirred-tank model (constant flow, ) Taking the Laplace transform yields: or letting Transfer functions 3 TransferTransfer FunctionFunction Heated stirred tank example + + + e.g. The block is called the transfer function relating Q(s) to T(s) 4 ProcessProcess ControlControl Time Domain Laplace Domain Process Modeling, Transfer function Experimentation and Modeling, Controller Implementation Design and Analysis Ability to understand dynamics in Laplace and time domains is extremely important in the study of process control 5 TransferTransfer functionsfunctions Transfer functions are generally expressed as a ratio of polynomials Where The polynomial is called the characteristic polynomial of Roots of are the zeroes of Roots of are the poles of 6 TransferTransfer functionfunction Order of underlying ODE is given by degree of characteristic polynomial e.g. First order processes Second order processes Order of the process is the degree of the characteristic (denominator) polynomial The relative order is the difference between the degree of the denominator polynomial and the degree of the numerator polynomial 7 TransferTransfer FunctionFunction Steady state behavior of the process obtained form the final value theorem e.g. First order process For a unit-step input, From the final value theorem, the ultimate value of is This implies that the limit exists, i.e. that the system is stable. 8 TransferTransfer functionfunction Transfer function is the unit impulse response e.g.
    [Show full text]
  • Time Response of Second Order Systems
    Time Response of Second Order Systems d 2 y(t) dy(t) M = f (t) − B − Ky(t) dt2 dt M(s2Y(s) − sy(0) − y'(0)) = F(s) − B(sY(s) − y(0))− KY(s) Let y'(0) = 0 2 Ms Y(s) + BsY(s) + KY(s) = Msy0 + By0 + F(s) Or (Ms+ B)y F(s) Y(s) = 0 + Ms2 + Bs+ K Ms2 + Bs+ K Consider t he first term only: (s + B/ M)y (s + 2ςω )y Y(s) = 0 = n 0 2 2 2 s + (B/ M)s + K / M s + 2ςωns +ωn ς = dimensionl ess damping ratio ωn = the natural frequency Where K B ω = ; ς = n M 2 KM 2 2 The characteristic equation s + 2ςωns +ωn has two roots : 2 s1 = −ςωn + jωn 1−ς 2 s2 = −ςω n − jωn 1−ς If ς >1⇒ roots are real If ς <1⇒ roots are complex (under damped) If ς =1⇒ same roots and real (critically damped) For unit step response : 1 y(t) =1− e−ςωnt sin(βω t +θ ) β n β β = 1−ς 2 , θ = tan −1( ) = cos−1 ς ς 1 −ζω t Step response: y(t) =1− e n sin(ω βt +θ ) β n 2 −1 where β = 1− ζ , θ = cos ζ Showing the step response with different damping coefficients Standard Performance measures Performance measures are usually defined in terms of the step response of a system as below: Swiftness of the response is measured by rise time , and peak time Swiftness of the response is measured by rise time T r , and peak time Tp For underdamped system, the Rise time T r (0-100% rise time) is useful, For overdamped systems, the the Peak time is not defined, and the (10-90 % rise time) is normally used Tr1 Peak time: T p Steady-state error: ess Settling time: T s Percent of Overshoot: M − fv P.O.
    [Show full text]
  • Time Response 4
    Time Response 4 Chapter Learning Outcomes After completing this chapter the student will be able to: • Use poles and zeros of transfer functions to determine the time response of a control system (Sections 4.1 –4.2) • Describe quantitatively the transient response of first-order systems (Section 4.3) • Write the general response of second-order systems given the pole location (Section 4.4) • Find the damping ratio and natural frequency of a second-order system (Section 4.5) • Find the settling time, peak time, percent overshoot, and rise time for an underdamped second-order system (Section 4.6) • Approximate higher-order systems and systems with zeros as first- or second- order systems (Sections 4.7 –4.8) • Describe the effects of nonlinearities on the system time response (Section 4.9) • Find the time response from the state-space representation (Sections 4.10 –4.11) Case Study Learning Outcomes You will be able to demonstrate your knowledge of the chapter objectives with case studies as follows: • Given the antenna azimuth position control system shown on the front endpapers, you will be able to (1) predict, by inspection, the form of the open-loop angular velocity response of the load to a step voltage input to 157 158 Chapter 4 Time Response the power ampli fier; (2) describe quantitatively the transient response of the open-loop system; (3) derive the expression for the open-loop angular velocity output for a step voltage input; (4) obtain the open-loop state-space representation; (5) plot the open-loop velocity step response using a computer simulation.
    [Show full text]
  • Lab # 4 Time Response Analysis
    Islamic University of Gaza Feedback Control Systems Lab Faculty of Engineering Eng. Tareq Abu Aisha Computer Engineering Dep. Lab # 4 Lab # 4 Time Response Analysis What is the Time Response …? It is an equation or a plot that describes the behavior of a system and contains much information about it with respect to time response specification as overshooting, settling time, peak time, rise time and steady state error. Time response is formed by the transient response and the steady state response. Time response = Transient response + Steady state response Transient time response (Natural response) describes the behavior of the system in its first short time until arrives the steady state value and this response will be our study focus. If the input is step function then the output or the response is called step time response and if the input is ramp, the response is called ramp time response … etc. Delay Time (Td): is the time required for the response to reach 50% of the final value. Rise Time (Tr): is the time required for the response to rise from 0 to 90% of the final value. Settling Time (Ts): is the time required for the response to reach and stay within a specified tolerance band ( 2% or 5%) of its final value. Peak Time (Tp): is the time required for the underdamped step response to reach the peak of time response (Yp) or the peak overshoot. Percent Overshoot (OS%): is the normalized difference between the response peak value and the steady value This characteristic is not found in a first order system and found in higher one for the underdamped step response.
    [Show full text]