A Phase Field Approach in the Numerical Study of the Elastic
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Livret Des Résumés Booklet of Abstracts
XXIXèmes Journées de linguistique d’Asie Orientale 29th Paris Meeting on East Asian Languages 4-5 juillet 2016 / July 4th-5th 2016 EHESS – 105 boulevard Raspail – 75006 Paris LIVRET DES RÉSUMÉS BOOKLET OF ABSTRACTS CRLAO CENTRE DE RECHERCHES LINGUISTIQUES SUR L’ASIE ORIENTALE Table des matières / Contents Conférence plénière / Keynote speech – Claire Saillard, Contact des langues entre le chinois et le truku (langue austronésienne de Taiwan): quelles grammaires en contact?....................................... 5 Arnaud Arslangul, Structures informationnelles et linguistiques du français et du chinois dans le discours de description spatiale……………………………………………………………………………………………………….. 6 Baik Junghye, Semantic-Pragmatic Development of a Spatial Noun The in Korean: From a Grammaticalization Perspective ……………………………………………………………………………………………………… 7 Daniel Chan & Yuan Hua-Hung, Verbal plurality: A view from Mandarin Chinese……………………………. 9 Chen Dandan 陳丹丹, 從“者”類後置型關係從句看漢語關係從句的特點……………………………….. 10 Choi Jiyoung, U-shaped development of inchoative states in Korean child language………………………. 11 Michel Ferlus, Incompatibilité entre des articulations continues dans les processus de registro- tonogenèse : exemples en vietique, en thai et en chinois…………………………………………………………………. 12 Kaori Furuya, Specification of the Person Feature in Pronominal Binding………………………………………… 13 Robert Iljic, Questions about questions (modal particles MA and NE in interrogative sentences)……. 14 Mark Irwin & Laurence Labrune, Les composés apophoniques en japonais…………………………………… 15 Ke Dan, -

Ideophones in Middle Chinese
KU LEUVEN FACULTY OF ARTS BLIJDE INKOMSTSTRAAT 21 BOX 3301 3000 LEUVEN, BELGIË ! Ideophones in Middle Chinese: A Typological Study of a Tang Dynasty Poetic Corpus Thomas'Van'Hoey' ' Presented(in(fulfilment(of(the(requirements(for(the(degree(of(( Master(of(Arts(in(Linguistics( ( Supervisor:(prof.(dr.(Jean=Christophe(Verstraete((promotor)( ( ( Academic(year(2014=2015 149(431(characters Abstract (English) Ideophones in Middle Chinese: A Typological Study of a Tang Dynasty Poetic Corpus Thomas Van Hoey This M.A. thesis investigates ideophones in Tang dynasty (618-907 AD) Middle Chinese (Sinitic, Sino- Tibetan) from a typological perspective. Ideophones are defined as a set of words that are phonologically and morphologically marked and depict some form of sensory image (Dingemanse 2011b). Middle Chinese has a large body of ideophones, whose domains range from the depiction of sound, movement, visual and other external senses to the depiction of internal senses (cf. Dingemanse 2012a). There is some work on modern variants of Sinitic languages (cf. Mok 2001; Bodomo 2006; de Sousa 2008; de Sousa 2011; Meng 2012; Wu 2014), but so far, there is no encompassing study of ideophones of a stage in the historical development of Sinitic languages. The purpose of this study is to develop a descriptive model for ideophones in Middle Chinese, which is compatible with what we know about them cross-linguistically. The main research question of this study is “what are the phonological, morphological, semantic and syntactic features of ideophones in Middle Chinese?” This question is studied in terms of three parameters, viz. the parameters of form, of meaning and of use. -

Huaqiang ZENG Team Leader and Principal Research Scientist
Huaqiang ZENG Team Leader and Principal Research Scientist +65 6824 7115 [email protected] Team Leader and Principal Research Scientist, NanoBio Lab, Singapore, 2019-present Team Leader and Principal Research Scientist, Institute of Bioengineering and Nanotechnology, Singapore, 2014-2019 Assistant Professor, National University of Singapore, 2006-2013 Postdoctoral Research Fellow, The Scripps Research Institute, USA, 2002-2006 Ph.D. in Organic Chemistry, The State University of New York at Buffalo, USA, 2002 B.S. in Chemical Physics, The University of Science and Technology of China, 1996 Publications 1. A. Roy, H. Joshi, R. Ye, J. Shen, F. Chen, A. Aksimentiev and H. Zeng, “Polyhydrazide‐Based Organic Nanotubes as Efficient and Selective Artificial Iodide Channels,” Angewandte Chemie International Edition, 132 (2020) 4836-4843. IF 12.102 2. J. Shen, J. Fan, R. Ye, N. Li, Y. Mu and H. Zeng, “Polypyridine-Based Helical Amide Foldamer Channels for Rapid Transport of Water and Proton with High Ion Rejection,” Angewandte Chemie International Edition, (2020) DOI: 10.1002/anie.202003512. IF 12.257 3. J. Shen, R. Ye, A. Romanies, A. Roy, F. Chen, C. Ren, Z. Liu and H. Zeng, “An Aquafoldmer-Based Aquaporin-Like Synthetic Water Channel,” Journal of the American Chemical Society, 142 (2020) 10050-10058. IF 14.695 4. H. Zeng, A. Roy, H. Joshi, R. Ye, J. Shen, F. Chen and A. Aksimentiev, “Polyhydrazide-Based Organic Nanotubes as Extremely Efficient and Highly Selective Artificial Iodide Channels,” Angew. Chem. Int. Ed., (2020) DOI: 10.1002/anie.201916287 5. H. Zeng, F. Chen, J. Shen, N. Li, A. -

Gěi ’Give’ in Beijing and Beyond Ekaterina Chirkova
Gěi ’give’ in Beijing and beyond Ekaterina Chirkova To cite this version: Ekaterina Chirkova. Gěi ’give’ in Beijing and beyond. Cahiers de linguistique - Asie Orientale, CRLAO, 2008, 37 (1), pp.3-42. hal-00336148 HAL Id: hal-00336148 https://hal.archives-ouvertes.fr/hal-00336148 Submitted on 2 Nov 2008 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Gěi ‘give’ in Beijing and beyond1 Katia Chirkova (CRLAO, CNRS) This article focuses on the various uses of gěi ‘give’, as attested in a corpus of spoken Beijing Mandarin collected by the author. These uses are compared to those in earlier attestations of Beijing Mandarin and to those in Greater Beijing Mandarin and in Jì-Lǔ Mandarin dialects. The uses of gěi in the corpus are demonstrated to be consistent with the latter pattern, where the primary function of gěi is that of indirect object marking and where, unlike Standard Mandarin, gěi is not additionally used as an agent marker or a direct object marker. Exceptions to this pattern in the corpus are explained as a recent development arisen through reanalysis. Key words : gěi, direct object marker, indirect object marker, agent marker, Beijing Mandarin, Northern Mandarin, typology. -
CHP-225 Terms
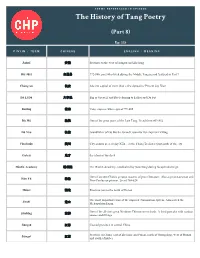
The History of Tang Poetry (Part 8) Ep. 225 Ānhuī 安徽 Province to the west of Jiangsu and Zhejiang Bái Jūyì 白居易 772-846, poet who lived during the Middle Tang period featured in Part 7 Cháng’an 长安 Ancient capital of more than a few dynasties/ Present day Xian Dà Lǐ Dù 大李杜 Big or Great Lǐ and Dù (referring to Li Bai and Du Fu) Dézōng 德宗 Tang emperor who reigned 779-805 Dù Mù 杜牧 One of the great poets of the Late Tang. Lived from 803-852 Dù Yòu 杜佑 Grandfather of Du Mu the Grand Councilor for emperor Dézōng Fánchuān 樊川 City around present day Xīān…in the Cháng’ān district just south of the city Guǐcái 鬼才 the talent of the devil Hànlín Academy 翰林院 The Hanlin Academy, established by Xuanzong during his splendid reign One of ancient China's greatest masters of prose literature. Also a great statesman and Hán Yù 韩愈 Neo-Confucian pioneer. Lived 768-824 Húběi 湖北 Province just to the north of Hunan The most important exam of the imperial examination system. Also called the Jinshi 进士 Metropolitan Exam One of the all-time great Northern Chinese street foods. A fried pancake with various jiānbǐng 煎餅 sauces and fillings Jiāngsū 江苏 Coastal province in central China Province in China, east of Zhejiang and Fujian, north of Guangdong, west of Hunan Jiāngxī 江西 and south of Hubei A poem of four lines of five to seven characters per line, with a strict tonal pattern and juéjù 绝句 rhyme scheme. Also known as a quatrain The second era of Xuanzong's reign, 713-741. -

Zeng Fanzhi Bibliography
G A G O S I A N Zeng Fanzhi Bibliography Selected Books and Catalogues: 2021 Chung, Gladys ed. Zeng Fanzhi Catalogue Raisonné: Volume I. Milan: Skira. 2016 Zeng, Fanzhi and Yuko Hasegawa. Zeng Fanzhi. New York: Gagosian Gallery. 2012 Zeng, Fanzhi, Zai-Fu and Robert E. Harris. Zeng Fanzhi. London: Gagosian Gallery. 2011 Zeng, Fanzhi. Zeng Fanzhi. Hong Kong: Gagosian Gallery. 2010 Zeng, Fanzhi, Fabien Fryns, and Richard Shift. Every Mark its Mask. Ostfildern: Hatje Cantz. 2009 Zeng, Fanzhi and William R. Acquavella. Zeng Fanzhi: Acquavella Contemporary Art. New York: Acquavella Contemporary Art. Zeng, Fanzhi. Zeng Fanzhi: April 2 – May 16, 2009: Acquavella Contemporary Art. New York: Acquavella Contemporary Art. 2007 Zeng, Fanzhi. Zeng Fanzhi, 1989-2007. Seoul, Korea: Gallery Hyundai. Zeng, Fanzhi; Lóránd Hegyi, and Peng Lu. Zeng Fanzhi. Saint-Etienne: Musée d'Art Moderne, Paris. 2006 Zeng, Fanzhi. The Paintings of Zeng Fanzhi. Shanghai: ShanghART. Selected Articles and Reviews: 2017 Zhao, William and Madeline Ross. “Masters of Reinvention.” Hong Kong Tatler, February 28. 2016 Qi, Lin. “Zeng show a time-travel retrospective.” China Daily, Aug 4. Qin, Amy. “Artist Zeng Fanzhi on the Evolution of His Work and China’s Art Market.” The New York Times, Sep 22. ---. “As China rises, top-selling painter looks to his roots.” France 24. October, 6. Tsui, Enid. “How China’s most bankable artist, Zeng Fanzhi, found new way to make art.” South China Morning Post. October 7. Chung, Stephy. “The man behind China’s million-dollar masks cares about art, not auctions.” CNN, October 20. Perlez, Jane. “How Zeng Fanzhi Became China’s Hottest Artist, and Why His Lawn Is So Green.” The New York Times, November 11. -

Curriculum Vitae
CURRICULUM VITAE Personal Information Name Zhou Guangsheng Gender male Position Title Professor Working Department College of Plant Science and Technology Email [email protected] the National Research Centre of Rapeseed Engineering and Technology Address College of Plant Science and Technology Huazhong Agricultural University Wuhan, Hubei 430070, P.R. China Tel +86-18627945966 Fax Research Interest Study on mechanism and technology of high yield and lodging resistance of rapeseed Education & Working Experience 1992-1996 Bachelor study of Agronomy of Huazhong Agricultural University (HZAU). 1996-1999 Master of Crop Cultivation and Farming System of HZAU. 1999-2007 Lecturer of HAZU. 2001-2006 Doctor of Crop Cultivation and Farming System of HZAU. 2007-2016 Associate Professor of HZAU. 2016 to now Professor of HZAU. Publications 1. Wang bo, Song Lijun, Wang Zongkai, Wang Jijun, Xiong Mingqing, Zhou Guang-Sheng*, Production and feeding technology of fodder- rapeseed in China. Chinese Journal of Oil Crop Sciences,2018,40(5):695-701 2. Xiaoyong Li, Qingsong Zuo, Haibin Chang, Guiping Bai, Jie Kuai*, Guangsheng Zhou*, Higher density planting benefits mechanical harvesting of rapeseed in the Yangtze River Basin of China,Field Crops Research,218(2018)97-105 3. Qingsong Zuo,Jie Kuai,Li Zhao, Zhan Hu, Jiangsheng Wu, Guangsheng Zhou *,The effect of sowing depth and soil compaction on the growth and yield of rapeseed in rice straw returning field, Field Crops Research,203(2017)47-54 4. Zuo Qing-Song, Liu Hao, Kuai Jie, Feng Qian-Nan, Feng Yun-Yan, Zhang Han-Xiao, Liu Jing-Yi, Yang Guang, Zhou Guang-Sheng*, Leng Suo-Hu. -

Historical Background of Wang Yang-Ming's Philosophy of Mind
Ping Dong Historical Background of Wang Yang-ming’s Philosophy of Mind From the Perspective of his Life Story Historical Background of Wang Yang-ming’s Philosophy of Mind Ping Dong Historical Background of Wang Yang-ming’s Philosophy of Mind From the Perspective of his Life Story Ping Dong Zhejiang University Hangzhou, Zhejiang, China Translated by Xiaolu Wang Liang Cai School of International Studies School of Foreign Language Studies Zhejiang University Ningbo Institute of Technology Hangzhou, Zhejiang, China Zhejiang University Ningbo, Zhejiang, China ISBN 978-981-15-3035-7 ISBN 978-981-15-3036-4 (eBook) https://doi.org/10.1007/978-981-15-3036-4 © The Editor(s) (if applicable) and The Author(s) 2020. This book is an open access publication. Open Access This book is licensed under the terms of the Creative Commons Attribution- NonCommercial-NoDerivatives 4.0 International License (http://creativecommons.org/licenses/by-nc- nd/4.0/), which permits any noncommercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if you modified the licensed material. You do not have permission under this license to share adapted material derived from this book or parts of it. The images or other third party material in this book are included in the book’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. -

What Were the Four Divisions of Middle Chinese?
What were the four Divisions of Middle Chinese ? Michel Ferlus To cite this version: Michel Ferlus. What were the four Divisions of Middle Chinese ? . Diachronica, Netherlands: John Benjamins, 2009, 26 (2), pp.184-213. 10.1075/dia.26.2.02fer. halshs-01581138v2 HAL Id: halshs-01581138 https://halshs.archives-ouvertes.fr/halshs-01581138v2 Submitted on 13 Nov 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Distributed under a Creative Commons Attribution - NonCommercial - ShareAlike| 4.0 International License What were the four Divisions of Middle Chinese ? (updated version) Michel FERLUS Centre National de la Recherche Scientifique, France The text presented here is the final result of a series of versions of our research on the four divisions (or grades) of ancient Chinese (Middle Chinese) : 1. (1998) Du chinois archaïque au chinois ancien : monosyllabisation et formation des syllabes tendu/lâche (Nouvelle théorie sur la phonétique historique du chinois), The 31st International Conference on Sino-Tibetan Languages and Linguistics, University of Lund, Swiden, Sept. 30th – Oct. 4th (22 pages). (Available: https://halshs.archives-ouvertes.fr/halshs-00927220) 2. (2006) What were the four divisions (děng) of Middle Chinese ?, The 39th International Conference on Sino-Tibetan Languages and Linguistics, University of Washington, Seattle, September 15-17 (12 pages). -

Surname Methodology in Defining Ethnic Populations : Chinese
Surname Methodology in Defining Ethnic Populations: Chinese Canadians Ethnic Surveillance Series #1 August, 2005 Surveillance Methodology, Health Surveillance, Public Health Division, Alberta Health and Wellness For more information contact: Health Surveillance Alberta Health and Wellness 24th Floor, TELUS Plaza North Tower P.O. Box 1360 10025 Jasper Avenue, STN Main Edmonton, Alberta T5J 2N3 Phone: (780) 427-4518 Fax: (780) 427-1470 Website: www.health.gov.ab.ca ISBN (on-line PDF version): 0-7785-3471-5 Acknowledgements This report was written by Dr. Hude Quan, University of Calgary Dr. Donald Schopflocher, Alberta Health and Wellness Dr. Fu-Lin Wang, Alberta Health and Wellness (Authors are ordered by alphabetic order of surname). The authors gratefully acknowledge the surname review panel members of Thu Ha Nguyen and Siu Yu, and valuable comments from Yan Jin and Shaun Malo of Alberta Health & Wellness. They also thank Dr. Carolyn De Coster who helped with the writing and editing of the report. Thanks to Fraser Noseworthy for assisting with the cover page design. i EXECUTIVE SUMMARY A Chinese surname list to define Chinese ethnicity was developed through literature review, a panel review, and a telephone survey of a randomly selected sample in Calgary. It was validated with the Canadian Community Health Survey (CCHS). Results show that the proportion who self-reported as Chinese has high agreement with the proportion identified by the surname list in the CCHS. The surname list was applied to the Alberta Health Insurance Plan registry database to define the Chinese ethnic population, and to the Vital Statistics Death Registry to assess the Chinese ethnic population mortality in Alberta. -

Imagery of Female Daoists in Tang and Song Poetry
Imagery of Female Daoists in Tang and Song Poetry by Yang Liu B.A. Changchun Normal University, 1985 M.A. Jilin University, 1994 A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY in THE FACULTY OF GRADUATE STUDIES (Asian Studies) THE UNIVERSITY OF BRITISH COLUMBIA (Vancouver) April, 2011 © Yang Liu, 2011 Abstract This dissertation involves a literary study that aims to understand the lives of female Daoists who lived from the eighth to the twelfth centuries in China. Together with an examination of the various individual qualities manifested in their poetry, this study includes related historical background, biographical information and a discussion of the aspirations and cultural life of the female clergy. Unlike some of the previous scholarship that has examined Daoist deities and mythical figures described in hagiographical texts and literary creations, or on topics such as the Divine Mother of the West and miscellaneous goddesses and fairies, this work takes the perspective of examining female Daoists as historical persons who lived in real Daoist convents. As such, this work concentrates on the assorted images of female Daoists presented in their own poetic works, including those of Yu Xuanji, Li Ye, Yuan Chun, Cao Wenyi and Sun Bu-er. Furthermore, this thesis also examines poetic works about female Daoists written by male literati from both inside and outside the Daoist religion. I do this in order to illustrate how elite men, the group with whom female Daoists interacted most frequently, appreciated and portrayed these special women and their poetry. I believe that a study of their works on Daoist women will not only allow us a better understanding of the nature and characters of female Daoists, but will also contribute to our knowledge of intellectual life in Tang and Song society. -

Student Intake Surname Given Names 1 Citizenship Fall 2015 LIN Yung
Student Intake Surname Given names 1 Citizenship Fall 2015 LIN Yung-Chun Taiwan Fall 2015 LEUNG Sung Hei Hong Kong Fall 2012 ABRAHAM Akshay India Fall 2015 ADIWINATA Theresa Indonesia Winter 2012 AL MAHDI Majid Saudi Arabia Fall 2015 ALNAQEH Sultan United Arab Emirates Winter 2012 ALQASSEM Marwan United Arab Emirates Fall 2013 ALSHAMSI Fares Khamis United Arab Emirates Winter 2014 AMIN Saqib Pakistan Fall 2015 ANAND Tarun India Fall 2014 AO Lin China Winter 2015 ASMARA Jildra Annisa Indonesia Fall 2015 AUNG Win Phyu Myanmar Winter 2014 AYE May Phyu Myanmar Fall 2012 MOHD AZMI Mariam Malaysia Winter 2015 BAI Chenguang China Fall 2012 BAI Yue China Fall 2013 BAO Yikun China Summer 2011 BATMUNKH Manlai Mongolia Winter 2012 BEIGI Shahriar Iran Fall 2014 BIDZHIEVA Ksenia Russian Federation Fall 2015 BINSALMA Faisal United Arab Emirates Fall 2015 BO Gin Gar Myanmar Fall 2014 BUBNOV Nikita Russian Federation Fall 2013 CAI Liming China Fall 2012 CAI Mengting China Summer 2014 CAI Pengcheng China Summer 2014 CAI Qing China Winter 2014 CAI Zhiwen China Fall 2013 CAO Fangyan China Fall 2013 CAO Ruijia China Winter 2014 CAO Yaning China Fall 2014 CAO Yiming China Fall 2015 CAO Zhengxiong China Fall 2013 CHAN Hoi Chi Hong Kong Fall 2013 CHANG Hang China Winter 2015 CHAO Hsin-Yu Taiwan Fall 2012 SINGH Chandan India Winter 2014 CHAU Venus Hong Kong Fall 2011 CHAN Yulun Taiwan Fall 2014 CHEN Bohan China Fall 2011 CHEN Chun China Fall 2014 CHEN Changzhen China Fall 2014 CHEN Guanqiu China Fall 2015 CHEN Huan China Winter 2014 CHEN Haoran China Fall 2014