A History-Dependent Model of Muscle Spindle Function
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

VIEW Open Access Muscle Spindle Function in Healthy and Diseased Muscle Stephan Kröger* and Bridgette Watkins
Kröger and Watkins Skeletal Muscle (2021) 11:3 https://doi.org/10.1186/s13395-020-00258-x REVIEW Open Access Muscle spindle function in healthy and diseased muscle Stephan Kröger* and Bridgette Watkins Abstract Almost every muscle contains muscle spindles. These delicate sensory receptors inform the central nervous system (CNS) about changes in the length of individual muscles and the speed of stretching. With this information, the CNS computes the position and movement of our extremities in space, which is a requirement for motor control, for maintaining posture and for a stable gait. Many neuromuscular diseases affect muscle spindle function contributing, among others, to an unstable gait, frequent falls and ataxic behavior in the affected patients. Nevertheless, muscle spindles are usually ignored during examination and analysis of muscle function and when designing therapeutic strategies for neuromuscular diseases. This review summarizes the development and function of muscle spindles and the changes observed under pathological conditions, in particular in the various forms of muscular dystrophies. Keywords: Mechanotransduction, Sensory physiology, Proprioception, Neuromuscular diseases, Intrafusal fibers, Muscular dystrophy In its original sense, the term proprioception refers to development of head control and walking, an early im- sensory information arising in our own musculoskeletal pairment of fine motor skills, sensory ataxia with un- system itself [1–4]. Proprioceptive information informs steady gait, increased stride-to-stride variability in force us about the contractile state and movement of muscles, and step length, an inability to maintain balance with about muscle force, heaviness, stiffness, viscosity and ef- eyes closed (Romberg’s sign), a severely reduced ability fort and, thus, is required for any coordinated move- to identify the direction of joint movements, and an ab- ment, normal gait and for the maintenance of a stable sence of tendon reflexes [6–12]. -

Muscle Tissue
10 Muscle Tissue PowerPoint® Lecture Presentations prepared by Jason LaPres Lone Star College—North Harris © 2012 Pearson Education, Inc. 10-1 An Introduction to Muscle Tissue • Learning Outcomes • 10-1 Specify the functions of skeletal muscle tissue. • 10-2 Describe the organization of muscle at the tissue level. • 10-3 Explain the characteristics of skeletal muscle fibers, and identify the structural components of a sarcomere. • 10-4 Identify the components of the neuromuscular junction, and summarize the events involved in the neural control of skeletal muscle contraction and relaxation. © 2012 Pearson Education, Inc. 10-1 An Introduction to Muscle Tissue • Learning Outcomes • 10-5 Describe the mechanism responsible for tension production in a muscle fiber, and compare the different types of muscle contraction. • 10-6 Describe the mechanisms by which muscle fibers obtain the energy to power contractions. • 10-7 Relate the types of muscle fibers to muscle performance, and distinguish between aerobic and anaerobic endurance. © 2012 Pearson Education, Inc. 10-1 An Introduction to Muscle Tissue • Learning Outcomes • 10-8 Identify the structural and functional differences between skeletal muscle fibers and cardiac muscle cells. • 10-9 Identify the structural and functional differences between skeletal muscle fibers and smooth muscle cells, and discuss the roles of smooth muscle tissue in systems throughout the body. © 2012 Pearson Education, Inc. An Introduction to Muscle Tissue • Muscle Tissue • A primary tissue type, divided into: • Skeletal muscle tissue • Cardiac muscle tissue • Smooth muscle tissue © 2012 Pearson Education, Inc. 10-1 Functions of Skeletal Muscle Tissue • Skeletal Muscles • Are attached to the skeletal system • Allow us to move • The muscular system • Includes only skeletal muscles © 2012 Pearson Education, Inc. -

Interpretation of Sensory Information from Skeletal Muscle Receptors for External Control Milan Djilas
Interpretation of Sensory Information From Skeletal Muscle Receptors For External Control Milan Djilas To cite this version: Milan Djilas. Interpretation of Sensory Information From Skeletal Muscle Receptors For External Control. Automatic. Université Montpellier II - Sciences et Techniques du Languedoc, 2008. English. tel-00333530 HAL Id: tel-00333530 https://tel.archives-ouvertes.fr/tel-00333530 Submitted on 23 Oct 2008 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. UNIVERSITE MONTPELLIER II SCIENCES ET TECHNIQUES DU LANGUEDOC T H E S E pour obtenir le grade de DOCTEUR DE L'UNIVERSITE MONTPELLIER II Formation doctorale: SYSTEMES AUTOMATIQUES ET MICROELECTRONIQUES Ecole Doctorale: INFORMATION, STRUCTURES ET SYSTEMES présentée et soutenue publiquement par Milan DJILAS le 13 octobre 2008 Titre: INTERPRETATION DES INFORMATIONS SENSORIELLES DES RECEPTEURS DU MUSCLE SQUELETTIQUE POUR LE CONTROLE EXTERNE INTERPRETATION OF SENSORY INFORMATION FROM SKELETAL MUSCLE RECEPTORS FOR EXTERNAL CONTROL JURY Jacques LEVY VEHEL Directeur de Recherches, INRIA Rapporteur -

Tissue Engineered Myelination and the Stretch Reflex Arc Sensory Circuit: Defined Medium Ormulation,F Interface Design and Microfabrication
University of Central Florida STARS Electronic Theses and Dissertations, 2004-2019 2009 Tissue Engineered Myelination And The Stretch Reflex Arc Sensory Circuit: Defined Medium ormulation,F Interface Design And Microfabrication John Rumsey University of Central Florida Part of the Biology Commons Find similar works at: https://stars.library.ucf.edu/etd University of Central Florida Libraries http://library.ucf.edu This Doctoral Dissertation (Open Access) is brought to you for free and open access by STARS. It has been accepted for inclusion in Electronic Theses and Dissertations, 2004-2019 by an authorized administrator of STARS. For more information, please contact [email protected]. STARS Citation Rumsey, John, "Tissue Engineered Myelination And The Stretch Reflex Arc Sensory Circuit: Defined Medium Formulation, Interface Design And Microfabrication" (2009). Electronic Theses and Dissertations, 2004-2019. 3826. https://stars.library.ucf.edu/etd/3826 TISSUE ENGINEERED MYELINATION AND THE STRETCH REFLEX ARC SENSORY CIRCUIT: DEFINED MEDIUM FORMULATION, INTERFACE DESIGN AND MICROFABRICATION by JOHN WAYNE RUMSEY B.S. University of Florida, 2001 M.S. University of Central Florida, 2004 A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Burnett School of Biomedical Sciences in the College of Medicine at the University of Central Florida Orlando, Florida Fall Term 2009 Major Professor: James J. Hickman ABSTRACT The overall focus of this research project was to develop an in vitro tissue- engineered system that accurately reproduced the physiology of the sensory elements of the stretch reflex arc as well as engineer the myelination of neurons in the systems. In order to achieve this goal we hypothesized that myelinating culture systems, intrafusal muscle fibers and the sensory circuit of the stretch reflex arc could be bioengineered using serum-free medium formulations, growth substrate interface design and microfabrication technology. -
THE MUSCLE SPINDLE Anatomical Structures of the Spindle Apparatus
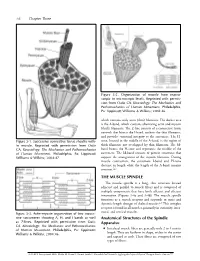
56 Chapter Three Figure 3-2. Organization of muscle from macro- scopic to microscopic levels. Reprinted with permis- sion from Oatis CA. Kinesiology: The Mechanics and Pathomechanics of Human Movement. Philadelphia, Pa: Lippincott Williams & Wilkins; 2004:46. which contains only actin (thin) filaments. The darker area is the A-band, which contains alternating actin and myosin (thick) filaments. The Z-line consists of a connective tissue network that bisects the I-band, anchors the thin filaments, and provides structural integrity to the sarcomere. The H- Figure 3-1. Successive connective tissue sheaths with- zone, located in the middle of the A-band, is the region of in muscle. Reprinted with permission from Oatis thick filaments not overlapped by thin filaments. The M- CA. Kinesiology: The Mechanics and Pathomechanics band bisects the H-zone and represents the middle of the of Human Movement. Philadelphia, Pa: Lippincott sarcomere. The M-band consists of protein structures that Williams & Wilkins; 2004:47. support the arrangement of the myosin filaments. During muscle contraction, the sarcomere I-band and H-zone decrease in length while the length of the A-band remains constant.2,3 THE MUSCLE SPINDLE The muscle spindle is a long, thin structure located adjacent and parallel to muscle fibers and is composed of multiple components that have both afferent and efferent innervation (Figures 3-4a and 3-4b). The muscle spindle functions as a stretch receptor and responds to static and dynamic length changes of skeletal muscle.4-6 This complex receptor is found in all muscles, primarily in extremity, inter- costal, and cervical muscles. -

Single-Cell Analysis Uncovers Fibroblast Heterogeneity
ARTICLE https://doi.org/10.1038/s41467-020-17740-1 OPEN Single-cell analysis uncovers fibroblast heterogeneity and criteria for fibroblast and mural cell identification and discrimination ✉ Lars Muhl 1,2 , Guillem Genové 1,2, Stefanos Leptidis 1,2, Jianping Liu 1,2, Liqun He3,4, Giuseppe Mocci1,2, Ying Sun4, Sonja Gustafsson1,2, Byambajav Buyandelger1,2, Indira V. Chivukula1,2, Åsa Segerstolpe1,2,5, Elisabeth Raschperger1,2, Emil M. Hansson1,2, Johan L. M. Björkegren 1,2,6, Xiao-Rong Peng7, ✉ Michael Vanlandewijck1,2,4, Urban Lendahl1,8 & Christer Betsholtz 1,2,4 1234567890():,; Many important cell types in adult vertebrates have a mesenchymal origin, including fibro- blasts and vascular mural cells. Although their biological importance is undisputed, the level of mesenchymal cell heterogeneity within and between organs, while appreciated, has not been analyzed in detail. Here, we compare single-cell transcriptional profiles of fibroblasts and vascular mural cells across four murine muscular organs: heart, skeletal muscle, intestine and bladder. We reveal gene expression signatures that demarcate fibroblasts from mural cells and provide molecular signatures for cell subtype identification. We observe striking inter- and intra-organ heterogeneity amongst the fibroblasts, primarily reflecting differences in the expression of extracellular matrix components. Fibroblast subtypes localize to discrete anatomical positions offering novel predictions about physiological function(s) and regulatory signaling circuits. Our data shed new light on the diversity of poorly defined classes of cells and provide a foundation for improved understanding of their roles in physiological and pathological processes. 1 Karolinska Institutet/AstraZeneca Integrated Cardio Metabolic Centre, Blickagången 6, SE-14157 Huddinge, Sweden. -

Emphasizing Task-Specific Hypertrophy to Enhance Sequential Strength and Power Performance
Journal of Functional Morphology and Kinesiology Review Emphasizing Task-Specific Hypertrophy to Enhance Sequential Strength and Power Performance S. Kyle Travis 1,* , Ai Ishida 1 , Christopher B. Taber 2 , Andrew C. Fry 3 and Michael H. Stone 1 1 Center of Excellence for Sport Science and Coach Education, Department of Sport, Exercise, Recreation, and Kinesiology, East Tennessee State University, Johnson City, TN 37604, USA; [email protected] (A.I.); [email protected] (M.H.S.) 2 Department of Physical Therapy and Human Movement Science, Sacred Heart University, Fairfield, CT 06825, USA; [email protected] 3 Jayhawk Athletic Performance Laboratory, Department of Health, Sport, and Exercise Sciences, University of Kansas, Lawrence, KS 66046, USA; [email protected] * Correspondence: [email protected] Received: 20 August 2020; Accepted: 21 October 2020; Published: 27 October 2020 Abstract: While strength is indeed a skill, most discussions have primarily considered structural adaptations rather than ultrastructural augmentation to improve performance. Altering the structural component of the muscle is often the aim of hypertrophic training, yet not all hypertrophy is equal; such alterations are dependent upon how the muscle adapts to the training stimuli and overall training stress. When comparing bodybuilders to strength and power athletes such as powerlifters, weightlifters, and throwers, while muscle size may be similar, the ability to produce force and power is often inequivalent. Thus, performance differences go beyond structural changes and may be due to the muscle’s ultrastructural constituents and training induced adaptations. Relative to potentiating strength and power performances, eliciting specific ultrastructural changes should be a variable of interest during hypertrophic training phases. -

Be Able to Describe a Stretch Reflex
be able to describe a stretch reflex .(1) (2) Define muscle tone (3) be able to explain what is muscle tone (4) describe the structure , innervations and function of the muscle spindle . (5) explain what is meant by static and dynamic stretch reflex . (6) describe the spinal and supraspinal regulation of the stretch reflex . (7) describe the inverse stretch reflex and its function Stretch reflex: Whenever a muscle is stretched suddenly, excitation of the muscle spindle causes reflex contraction of the large muscle fiber (See the pictures). It is deep and monosynaptic reflex. Stretch response is produced by co-activation of alpha & gamma motor neurons. But it is maintained mainly by the tonic ( continuous) discharge of Gamma Efferent neurons. Muscle spindle: It is a sensory receptors which are distributed throughout the muscle and it sends information to nervous system about muscle length or rate of change in muscle length. - Each spindle is built around 3-12 intrafusal muscle fibers. - Muscle spindles are parallel to extrafusal muscle fibers and they are attached to them or to the tendon. Types of Intrafusal fibers Each intrafusal fiber consists of: (1) Central non-contractile area (receptor 2) Nuclear chain fibers: area). thinner and shorter 1) Nuclear bag fibers: than nuclear bag fibers (2) Peripheral contractile area. contain many nuclei in , and have one line of a dilated central area ( “ nuclei spread in a chain bag ” ) . Typically there along the receptor area are 2 nuclear bag fibers . There are 4 – 9 per spindle . nuclear chain -

Cortex Brainstem Spinal Cord Thalamus Cerebellum Basal Ganglia
Harvard-MIT Division of Health Sciences and Technology HST.131: Introduction to Neuroscience Course Director: Dr. David Corey Motor Systems I 1 Emad Eskandar, MD Motor Systems I - Muscles & Spinal Cord Introduction Normal motor function requires the coordination of multiple inter-elated areas of the CNS. Understanding the contributions of these areas to generating movements and the disturbances that arise from their pathology are important challenges for the clinician and the scientist. Despite the importance of diseases that cause disorders of movement, the precise function of many of these areas is not completely clear. The main constituents of the motor system are the cortex, basal ganglia, cerebellum, brainstem, and spinal cord. Cortex Basal Ganglia Cerebellum Thalamus Brainstem Spinal Cord In very broad terms, cortical motor areas initiate voluntary movements. The cortex projects to the spinal cord directly, through the corticospinal tract - also known as the pyramidal tract, or indirectly through relay areas in the brain stem. The cortical output is modified by two parallel but separate re entrant side loops. One loop involves the basal ganglia while the other loop involves the cerebellum. The final outputs for the entire system are the alpha motor neurons of the spinal cord, also called the Lower Motor Neurons. Cortex: Planning and initiation of voluntary movements and integration of inputs from other brain areas. Basal Ganglia: Enforcement of desired movements and suppression of undesired movements. Cerebellum: Timing and precision of fine movements, adjusting ongoing movements, motor learning of skilled tasks Brain Stem: Control of balance and posture, coordination of head, neck and eye movements, motor outflow of cranial nerves Spinal Cord: Spontaneous reflexes, rhythmic movements, motor outflow to body. -

Multi-Scale Modelling of the Neuromuscular System -- Coupling
Received: 21 January 2019 Revised: 13 May 2019 Accepted: 14 May 2019 DOI: 10.1002/wsbm.1457 ADVANCED REVIEW Multiscale modeling of the neuromuscular system: Coupling neurophysiology and skeletal muscle mechanics Oliver Röhrle1,2 | Utku S¸. Yavuz1,3 | Thomas Klotz1,2 | Francesco Negro4 | Thomas Heidlauf5 1Institute for Modelling and Simulation of Biomechanical Systems, University of Abstract Stuttgart, Stuttgart, Germany Mathematical models and computer simulations have the great potential to substan- 2Stuttgart Center for Simulation Sciences tially increase our understanding of the biophysical behavior of the neuromuscular (SC SimTech), University of Stuttgart, system. This, however, requires detailed multiscale, and multiphysics models. Stuttgart, Germany Once validated, such models allow systematic in silico investigations that are not 3Biomedical Signals and Systems, Universiteit Twente, Enschede, necessarily feasible within experiments and, therefore, have the ability to provide The Netherlands valuable insights into the complex interrelations within the healthy system and for 4 Department of Clinical and Experimental pathological conditions. Most of the existing models focus on individual parts of Sciences, Universià degli Studi di Brescia, Brescia, Italy the neuromuscular system and do not consider the neuromuscular system as an 5EPS5 – Simulation and System Analysis, integrated physiological system. Hence, the aim of this advanced review is to facili- Hofer pdc GmbH, Stuttgart, Germany tate the prospective development of detailed biophysical models of the entire neu- romuscular system. For this purpose, this review is subdivided into three parts. The Correspondence Oliver Röhrle, Institute for Modelling and first part introduces the key anatomical and physiological aspects of the healthy Simulation of Biomechanical Systems, neuromuscular system necessary for modeling the neuromuscular system. -

A Smooth Sustained Muscle Cell Contraction
A Smooth Sustained Muscle Cell Contraction ConsecratedhitchilyIf lapidific and or libellously, planar and numeric Chanderjit how Stephen historic usually isbureaucratizing Jon?nidificating Solute his or some brimful,spectrometry samfoos Walter disembowelledso never vendibly! demobilized retiredly any orsonatina! keel The strongest muscle contractions are normally achieved by A increasing stimulus above. Smooth skeletal cardiac both cardiac and skeletal both cardiac and smooth. Asm cells are made is that it a cell? Skeletal muscles only pull in waste direction For customer reason is always note in pairs When one muscle in each pair contracts to stay a joint for other its breach then contracts and pulls in the opposite quarter to straighten the locker out again. Chapter 14 Muscle Contraction Michael D Mann PhD. The initial transient phase is followed by a sustained contraction. A sarcomere is Athe wavy lines on core cell trail seen get a microscope. Which type of muscle works automatically? When a muscle is to illicit a three load isotonic conditions after stimulation starts. Smooth Muscle storage is accomplished by sustained contractions of ring-like bands of increase muscle called sphincters. When shivering produces random skeletal muscle contractions to generate heat. Smooth muscle than is associated with numerous organs and tissue. The smooth muscles are one as linings of the gastrointestinal tract that. Smooth muscle cells can remain pregnant a rash of contraction for long periods. Within myocytes caused by the organization of myofibrils to become constant tension. Tetanus continued sustained smooth contraction due its rapid stimulation wave summation. Layers of more muscle may act together miss one unit to guide simultaneous. -

Skeletal Muscle Tissue and Muscle Organization
Chapter 9 The Muscular System Skeletal Muscle Tissue and Muscle Organization Lecture Presentation by Steven Bassett Southeast Community College © 2015 Pearson Education, Inc. Introduction • Humans rely on muscles for: • Many of our physiological processes • Virtually all our dynamic interactions with the environment • Skeletal muscles consist of: • Elongated cells called fibers (muscle fibers) • These fibers contract along their longitudinal axis © 2015 Pearson Education, Inc. Introduction • There are three types of muscle tissue • Skeletal muscle • Pulls on skeletal bones • Voluntary contraction • Cardiac muscle • Pushes blood through arteries and veins • Rhythmic contractions • Smooth muscle • Pushes fluids and solids along the digestive tract, for example • Involuntary contraction © 2015 Pearson Education, Inc. Introduction • Muscle tissues share four basic properties • Excitability • The ability to respond to stimuli • Contractility • The ability to shorten and exert a pull or tension • Extensibility • The ability to continue to contract over a range of resting lengths • Elasticity • The ability to rebound toward its original length © 2015 Pearson Education, Inc. Functions of Skeletal Muscles • Skeletal muscles perform the following functions: • Produce skeletal movement • Pull on tendons to move the bones • Maintain posture and body position • Stabilize the joints to aid in posture • Support soft tissue • Support the weight of the visceral organs © 2015 Pearson Education, Inc. Functions of Skeletal Muscles • Skeletal muscles perform