DOCSLIB.ORG

Long-Term Variability of the Sun in the Context of Solar-Analog Stars

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Long-Term Variability of the Sun in the Context of Solar-Analog Stars LONG-TERM VARIABILITY OF THE SUN IN THE CONTEXT OF SOLAR-ANALOG STARS by Ricky Alan Egeland A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Physics MONTANA STATE UNIVERSITY Bozeman, Montana April, 2017 c COPYRIGHT by Ricky Alan Egeland 2017 All Rights Reserved ii DEDICATION To those of our ancestors who diligently chronicled Nature. iii ACKNOWLEDGEMENTS I thank God, for His inspiration on a starry night in Brazil, for His wonderous creation, and for giving us some capacity to understand it. Thanks to my parents John and Bonnie for their care and wisdom. Thanks to my loving wife Patricia for her support, as well as her patience and confidence, which at times were greater than my own. Thanks to my daughter Emilie, for being a constant joy. Thanks to Dr. David DeMuth, who gave me the opportunity to work in physics research and computer programming at a time when I knew nothing. Thanks to my undergraduate advisor and supervisor, Dr. Roger Rusack, to my early mentor in solar physics, Dr. David McKenzie, and to my mentor and colleague Dr. Travis S. Metcalfe. Thanks to my excellent teachers in physics, Dr. Joseph Kapusta and Dr. Paul Crowell of the University of Minnesota, and Dr. Carla Riedel, Dr. Charles Kankelborg, and Dr. Dana Longcope of Montana State University. Thanks to Dr. Willie Soon, Dr. Sallie L. Baliunas, Dr. Jeffrey C. Hall, Gregory W. Henry, Dr. Alexei Pevtsov, Dr. Christoffer Karoff, and Dr. Timothy W. Henry for graciously sharing and explaining the various datasets used in this work. Thanks to Dr. Robert A. Donahue and Dr. Douglas K. Duncan for helpful conversations on the technical details and history of the Mount Wilson HK project. Thanks to my advisors Dr. Petrus C. H. Martens and Dr. Phillip G. Judge for guiding me toward a research topic that I found so stimulating, and for the many useful discussions. Funding Acknowledgment This work was kindly supported by the Gordon A. Newkirk Fellowship at the High Altitude Observatory of the National Center for Atmospheric Research in Boulder, Colorado. iv TABLE OF CONTENTS 1. INTRODUCTION ........................................................................................1 1.1 The Corrupt Sun is a Nearby Star ...........................................................1 1.2 The Solar Dynamo Problem ....................................................................7 1.2.1 Mean-Field Dynamo Models ....................................................... 10 1.2.2 Global Convective MHD Dynamo Models.................................... 13 1.3 Stellar \Dynamo Experiments".............................................................. 18 1.3.1 Indices of Chromospheric Activity............................................... 22 1.3.2 The Solar-Stellar Connection ...................................................... 24 1.3.3 The Vaughan-Preston Gap ......................................................... 25 1.3.4 Rotation and Differential Rotation .............................................. 25 1.3.5 Rotation-Activity-Age Relationships ........................................... 27 1.3.6 Patterns of Long-term Variability................................................ 30 1.3.7 \Maunder Minimum" Stars ........................................................ 32 1.3.8 Search for \Solar Twins" ............................................................ 33 1.3.9 Variations in Visible Bands......................................................... 35 1.3.10 Cycle Period Patterns and Dynamo Theory ................................. 36 1.3.11 Second-Generation Stellar Activity Surveys ................................. 40 1.4 Organization of this Work ..................................................................... 42 1.4.1 Related Publications and Contributions....................................... 43 2. THE SUN AS A STAR: THE SOLAR S-INDEX TIME SERIES ...................45 2.1 The S-index Scale ................................................................................. 45 2.2 Previous Solar S Proxies ....................................................................... 47 2.3 Observations ........................................................................................ 51 2.3.1 Mount Wilson Observatory HKP-1 and HKP-2............................ 51 2.3.2 NSO Sacramento Peak K-line Program........................................ 52 2.3.3 Kodaikanal Observatory Ca K Spectroheliograms......................... 53 2.3.4 Lowell Observatory Solar Stellar Spectrograph............................. 54 2.4 Analysis............................................................................................... 57 2.4.1 Cycle 23 Direct Measurements .................................................... 57 2.4.2 Cycle Shape Model Fit for Cycle 23 ............................................ 58 2.4.3 S(K) Proxy Using NSO/SP K Emission Index ............................ 62 2.4.4 Comparison with SSS Solar Data ................................................ 64 2.4.5 Calibrating HKP-1 Measurements............................................... 66 2.4.6 Composite MWO and NSO/SP S(K) Time Series........................ 69 0 2.4.7 Conversion to log(RHK) .............................................................. 72 2.5 Linearity of S with K ........................................................................... 72 2.6 Discussion ............................................................................................ 76 v TABLE OF CONTENTS | CONTINUED 3. CASE STUDY: THE YOUNG SOLAR ANALOG HD 30495.........................81 3.1 Solar and Stellar Short-Period Variations ............................................... 81 3.2 HD 30495 Properties and Previous Observations..................................... 82 3.3 Activity Analysis .................................................................................. 85 3.4 Simple Cycle Model .............................................................................. 94 3.5 Short-Period Time-Frequency Analysis................................................... 98 3.6 Rotation ............................................................................................ 102 3.7 Discussion .......................................................................................... 105 4. LONG-TERM VARIABILITY OF SOLAR-ANALOG STARS..................... 109 4.1 Sample Selection and Characterization................................................. 110 4.1.1 Binary Stars and Characterizing HD 81809................................ 110 4.1.2 Properties of the Sample .......................................................... 113 4.2 SSS Calibration to the MWO S-index Scale ......................................... 118 4.3 Activity of 18 Sco Compared to the Sun .............................................. 123 4.4 Amplitude of Variability...................................................................... 124 4.5 A New Cycle Quality Metric ............................................................... 134 4.6 Analysis of Cyclic Variability............................................................... 141 4.7 Cycle Period and Rotation Period........................................................ 146 5. THE SOLAR CYCLE IN CONTEXT ........................................................ 151 5.1 Variability Classes and FAP Grade Cycle Quality................................. 151 5.2 Binaries in the B95 Sample ................................................................. 154 5.3 Properties of the MWO Sample........................................................... 156 5.4 Variability Class by Spectral Group and Activity.................................. 160 5.5 Variability Class by Rotation and Rossby Number................................ 166 5.6 Hypotheses on the Properties Resulting in Sun-like Cycles .................... 170 5.6.1 Hypothesis Testing with the Solar Analog Ensemble................... 178 5.7 FAP Grade and Cycle Period .............................................................. 180 5.8 Summary of Results............................................................................ 181 6. CONCLUSION......................................................................................... 185 REFERENCES CITED.................................................................................. 193 APPENDICES .............................................................................................. 217 APPENDIX A: Cycle Model Monte Carlo Experiments ............................ 218 vi TABLE OF CONTENTS | CONTINUED APPENDIX B: Ensemble Time Series and Periodograms .......................... 224 vii LIST OF TABLES Table Page 2.1 S(K) Transformations ...................................................................... 48 2.2 Solar Cycle Shape Parameters and S-index Measurements .................. 71 0 2.3 Solar Cycle Measurements in log(RHK) .............................................. 73 3.1 HD 30495 Properties ......................................................................... 84 3.2 HD 30495 Cycle Properties................................................................ 96 4.1 Solar Analog Ensemble Properties.................................................... 115 4.2 Solar Analog Ensemble Statistics ..................................................... 127 4.3 Cycle Quality Metric Test Cases ...................................................... 140 4.4 Solar Analog Ensemble Variability Periods ....................................... 142 4.5 Solar
Load more

Recommended publications
  • Astronomie in Theorie Und Praxis 8. Auflage in Zwei Bänden Erik Wischnewski
    Astronomie in Theorie und Praxis 8. Auflage in zwei Bänden Erik Wischnewski Inhaltsverzeichnis 1 Beobachtungen mit bloßem Auge 37 Motivation 37 Hilfsmittel 38 Drehbare Sternkarte Bücher und Atlanten Kataloge Planetariumssoftware Elektronischer Almanach Sternkarten 39 2 Atmosphäre der Erde 49 Aufbau 49 Atmosphärische Fenster 51 Warum der Himmel blau ist? 52 Extinktion 52 Extinktionsgleichung Photometrie Refraktion 55 Szintillationsrauschen 56 Angaben zur Beobachtung 57 Durchsicht Himmelshelligkeit Luftunruhe Beispiel einer Notiz Taupunkt 59 Solar-terrestrische Beziehungen 60 Klassifizierung der Flares Korrelation zur Fleckenrelativzahl Luftleuchten 62 Polarlichter 63 Nachtleuchtende Wolken 64 Haloerscheinungen 67 Formen Häufigkeit Beobachtung Photographie Grüner Strahl 69 Zodiakallicht 71 Dämmerung 72 Definition Purpurlicht Gegendämmerung Venusgürtel Erdschattenbogen 3 Optische Teleskope 75 Fernrohrtypen 76 Refraktoren Reflektoren Fokus Optische Fehler 82 Farbfehler Kugelgestaltsfehler Bildfeldwölbung Koma Astigmatismus Verzeichnung Bildverzerrungen Helligkeitsinhomogenität Objektive 86 Linsenobjektive Spiegelobjektive Vergütung Optische Qualitätsprüfung RC-Wert RGB-Chromasietest Okulare 97 Zusatzoptiken 100 Barlow-Linse Shapley-Linse Flattener Spezialokulare Spektroskopie Herschel-Prisma Fabry-Pérot-Interferometer Vergrößerung 103 Welche Vergrößerung ist die Beste? Blickfeld 105 Lichtstärke 106 Kontrast Dämmerungszahl Auflösungsvermögen 108 Strehl-Zahl Luftunruhe (Seeing) 112 Tubusseeing Kuppelseeing Gebäudeseeing Montierungen 113 Nachführfehler
    [Show full text]
  • Lurking in the Shadows: Wide-Separation Gas Giants As Tracers of Planet Formation
    Lurking in the Shadows: Wide-Separation Gas Giants as Tracers of Planet Formation Thesis by Marta Levesque Bryan In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy CALIFORNIA INSTITUTE OF TECHNOLOGY Pasadena, California 2018 Defended May 1, 2018 ii © 2018 Marta Levesque Bryan ORCID: [0000-0002-6076-5967] All rights reserved iii ACKNOWLEDGEMENTS First and foremost I would like to thank Heather Knutson, who I had the great privilege of working with as my thesis advisor. Her encouragement, guidance, and perspective helped me navigate many a challenging problem, and my conversations with her were a consistent source of positivity and learning throughout my time at Caltech. I leave graduate school a better scientist and person for having her as a role model. Heather fostered a wonderfully positive and supportive environment for her students, giving us the space to explore and grow - I could not have asked for a better advisor or research experience. I would also like to thank Konstantin Batygin for enthusiastic and illuminating discussions that always left me more excited to explore the result at hand. Thank you as well to Dimitri Mawet for providing both expertise and contagious optimism for some of my latest direct imaging endeavors. Thank you to the rest of my thesis committee, namely Geoff Blake, Evan Kirby, and Chuck Steidel for their support, helpful conversations, and insightful questions. I am grateful to have had the opportunity to collaborate with Brendan Bowler. His talk at Caltech my second year of graduate school introduced me to an unexpected population of massive wide-separation planetary-mass companions, and lead to a long-running collaboration from which several of my thesis projects were born.
    [Show full text]
  • Durham E-Theses
    Durham E-Theses First visibility of the lunar crescent and other problems in historical astronomy. Fatoohi, Louay J. How to cite: Fatoohi, Louay J. (1998) First visibility of the lunar crescent and other problems in historical astronomy., Durham theses, Durham University. Available at Durham E-Theses Online: http://etheses.dur.ac.uk/996/ Use policy The full-text may be used and/or reproduced, and given to third parties in any format or medium, without prior permission or charge, for personal research or study, educational, or not-for-prot purposes provided that: • a full bibliographic reference is made to the original source • a link is made to the metadata record in Durham E-Theses • the full-text is not changed in any way The full-text must not be sold in any format or medium without the formal permission of the copyright holders. Please consult the full Durham E-Theses policy for further details. Academic Support Oce, Durham University, University Oce, Old Elvet, Durham DH1 3HP e-mail: [email protected] Tel: +44 0191 334 6107 http://etheses.dur.ac.uk me91 In the name of Allah, the Gracious, the Merciful >° 9 43'' 0' eji e' e e> igo4 U61 J CO J: lic 6..ý v Lo ý , ý.,, "ý J ýs ýºý. ur ý,r11 Lýi is' ý9r ZU LZJE rju No disaster can befall on the earth or in your souls but it is in a book before We bring it into being; that is easy for Allah. In order that you may not grieve for what has escaped you, nor be exultant at what He has given you; and Allah does not love any prideful boaster.
    [Show full text]
  • The Remarkable Solar Twin HIP 56948: a Prime Target in the Quest for Other
    Astronomy & Astrophysics manuscript no. keck56948˙2012˙04˙06 c ESO 2018 October 30, 2018 The remarkable solar twin HIP 56948: a prime target in the quest for other Earths ⋆ Jorge Mel´endez1, Maria Bergemann2, Judith G. Cohen3, Michael Endl4, Amanda I. Karakas5, Iv´an Ram´ırez4,6, William D. Cochran4, David Yong5, Phillip J. MacQueen4, Chiaki Kobayashi5⋆⋆, and Martin Asplund5 1 Departamento de Astronomia do IAG/USP, Universidade de S˜ao Paulo, Rua do Mat˜ao 1226, Cidade Universit´aria, 05508-900 S˜ao Paulo, SP, Brazil. e-mail: [email protected] 2 Max Planck Institute for Astrophysics, Postfach 1317, 85741 Garching, Germany 3 Palomar Observatory, Mail Stop 105-24, California Institute of Technology, Pasadena, California 91125, USA 4 McDonald Observatory, The University of Texas at Austin, Austin, TX 78712, USA 5 Research School of Astronomy and Astrophysics, The Australian National University, Cotter Road, Weston, ACT 2611, Australia 6 The Observatories of the Carnegie Institution for Science, 813 Santa Barbara Street, Pasadena, CA 91101, USA Received ...; accepted ... ABSTRACT Context. The Sun shows abundance anomalies relative to most solar twins. If the abundance peculiarities are due to the formation of inner rocky planets, that would mean that only a small fraction of solar type stars may host terrestrial planets. Aims. In this work we study HIP 56948, the best solar twin known to date, to determine with an unparalleled precision how similar is to the Sun in its physical properties, chemical composition and planet architecture. We explore whether the abundances anomalies may be due to pollution from stellar ejecta or to terrestrial planet formation.
    [Show full text]
  • Li Abundances in F Stars: Planets, Rotation, and Galactic Evolution,
    A&A 576, A69 (2015) Astronomy DOI: 10.1051/0004-6361/201425433 & c ESO 2015 Astrophysics Li abundances in F stars: planets, rotation, and Galactic evolution, E. Delgado Mena1,2, S. Bertrán de Lis3,4, V. Zh. Adibekyan1,2,S.G.Sousa1,2,P.Figueira1,2, A. Mortier6, J. I. González Hernández3,4,M.Tsantaki1,2,3, G. Israelian3,4, and N. C. Santos1,2,5 1 Centro de Astrofisica, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal e-mail: [email protected] 2 Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal 3 Instituto de Astrofísica de Canarias, C/via Lactea, s/n, 38200 La Laguna, Tenerife, Spain 4 Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain 5 Departamento de Física e Astronomía, Faculdade de Ciências, Universidade do Porto, Portugal 6 SUPA, School of Physics and Astronomy, University of St. Andrews, St. Andrews KY16 9SS, UK Received 28 November 2014 / Accepted 14 December 2014 ABSTRACT Aims. We aim, on the one hand, to study the possible differences of Li abundances between planet hosts and stars without detected planets at effective temperatures hotter than the Sun, and on the other hand, to explore the Li dip and the evolution of Li at high metallicities. Methods. We present lithium abundances for 353 main sequence stars with and without planets in the Teff range 5900–7200 K. We observed 265 stars of our sample with HARPS spectrograph during different planets search programs. We observed the remaining targets with a variety of high-resolution spectrographs.
    [Show full text]
  • Naming the Extrasolar Planets
    Naming the extrasolar planets W. Lyra Max Planck Institute for Astronomy, K¨onigstuhl 17, 69177, Heidelberg, Germany [email protected] Abstract and OGLE-TR-182 b, which does not help educators convey the message that these planets are quite similar to Jupiter. Extrasolar planets are not named and are referred to only In stark contrast, the sentence“planet Apollo is a gas giant by their assigned scientific designation. The reason given like Jupiter” is heavily - yet invisibly - coated with Coper- by the IAU to not name the planets is that it is consid- nicanism. ered impractical as planets are expected to be common. I One reason given by the IAU for not considering naming advance some reasons as to why this logic is flawed, and sug- the extrasolar planets is that it is a task deemed impractical. gest names for the 403 extrasolar planet candidates known One source is quoted as having said “if planets are found to as of Oct 2009. The names follow a scheme of association occur very frequently in the Universe, a system of individual with the constellation that the host star pertains to, and names for planets might well rapidly be found equally im- therefore are mostly drawn from Roman-Greek mythology. practicable as it is for stars, as planet discoveries progress.” Other mythologies may also be used given that a suitable 1. This leads to a second argument. It is indeed impractical association is established. to name all stars. But some stars are named nonetheless. In fact, all other classes of astronomical bodies are named.
    [Show full text]
  • Livre-Ovni.Pdf
    UN MONDE BIZARRE Le livre des étranges Objets Volants Non Identifiés Chapitre 1 Paranormal Le paranormal est un terme utilisé pour qualifier un en- mé n'est pas considéré comme paranormal par les semble de phénomènes dont les causes ou mécanismes neuroscientifiques) ; ne sont apparemment pas explicables par des lois scien- tifiques établies. Le préfixe « para » désignant quelque • Les différents moyens de communication avec les chose qui est à côté de la norme, la norme étant ici le morts : naturels (médiumnité, nécromancie) ou ar- consensus scientifique d'une époque. Un phénomène est tificiels (la transcommunication instrumentale telle qualifié de paranormal lorsqu'il ne semble pas pouvoir que les voix électroniques); être expliqué par les lois naturelles connues, laissant ain- si le champ libre à de nouvelles recherches empiriques, à • Les apparitions de l'au-delà (fantômes, revenants, des interprétations, à des suppositions et à l'imaginaire. ectoplasmes, poltergeists, etc.) ; Les initiateurs de la parapsychologie se sont donné comme objectif d'étudier d'une manière scientifique • la cryptozoologie (qui étudie l'existence d'espèce in- ce qu'ils considèrent comme des perceptions extra- connues) : classification assez injuste, car l'objet de sensorielles et de la psychokinèse. Malgré l'existence de la cryptozoologie est moins de cultiver les mythes laboratoires de parapsychologie dans certaines universi- que de chercher s’il y a ou non une espèce animale tés, notamment en Grande-Bretagne, le paranormal est inconnue réelle derrière une légende ; généralement considéré comme un sujet d'étude peu sé- rieux. Il est en revanche parfois associé a des activités • Le phénomène ovni et ses dérivés (cercle de culture).
    [Show full text]
  • Correlations Between the Stellar, Planetary, and Debris Components of Exoplanet Systems Observed by Herschel⋆
    A&A 565, A15 (2014) Astronomy DOI: 10.1051/0004-6361/201323058 & c ESO 2014 Astrophysics Correlations between the stellar, planetary, and debris components of exoplanet systems observed by Herschel J. P. Marshall1,2, A. Moro-Martín3,4, C. Eiroa1, G. Kennedy5,A.Mora6, B. Sibthorpe7, J.-F. Lestrade8, J. Maldonado1,9, J. Sanz-Forcada10,M.C.Wyatt5,B.Matthews11,12,J.Horner2,13,14, B. Montesinos10,G.Bryden15, C. del Burgo16,J.S.Greaves17,R.J.Ivison18,19, G. Meeus1, G. Olofsson20, G. L. Pilbratt21, and G. J. White22,23 (Affiliations can be found after the references) Received 15 November 2013 / Accepted 6 March 2014 ABSTRACT Context. Stars form surrounded by gas- and dust-rich protoplanetary discs. Generally, these discs dissipate over a few (3–10) Myr, leaving a faint tenuous debris disc composed of second-generation dust produced by the attrition of larger bodies formed in the protoplanetary disc. Giant planets detected in radial velocity and transit surveys of main-sequence stars also form within the protoplanetary disc, whilst super-Earths now detectable may form once the gas has dissipated. Our own solar system, with its eight planets and two debris belts, is a prime example of an end state of this process. Aims. The Herschel DEBRIS, DUNES, and GT programmes observed 37 exoplanet host stars within 25 pc at 70, 100, and 160 μm with the sensitiv- ity to detect far-infrared excess emission at flux density levels only an order of magnitude greater than that of the solar system’s Edgeworth-Kuiper belt. Here we present an analysis of that sample, using it to more accurately determine the (possible) level of dust emission from these exoplanet host stars and thereafter determine the links between the various components of these exoplanetary systems through statistical analysis.
    [Show full text]
  • La Photosynthèse Serait Apparue Chez Certains Organismes Primitifs Entre 2.800 Et -2.400 Millions D’Années Si L’On En Croit Certaines Archives Géologiques Terrestres
    La photosynthèse serait apparue chez certains organismes primitifs entre 2.800 et -2.400 millions d’années si l’on en croit certaines archives géologiques terrestres. Mais certains la font remonter bien plus tôt en faisant l’hypothèse que les stromatolites que l’on retrouve dans des couches plus anciennes encore sont bien le produit d’une activité biologique. Actuellement, nous n’en sommes sûrs que pour ceux datant de -2.724 millions d’années mais des stromatolites existaient déjà sur Terre il y a 3,5 milliards d’années environ. Quoiqu'il en soit, une certitude demeure, concernant les immenses dépôts de fer du bassin de Hamersley en Australie. Ils datent de l’époque du Sidérien alors que la surface des continents était devenue suffisamment importante pour que se forment des mers peu profondes entourées de grande plates-formes continentales. Les conditions étaient remplies pour que de grands tapis de bactéries construisent des stromatolites en quantités importantes et dégagent massivement de l’oxygène par photosynthèse. Ce gaz corrosif a alors pu oxyder le fer en solution dans les océans et entraîner sa précipitation sous forme d’hydroxyde de fer, de carbonate de fer, de silicate ou de sulfures, selon des variations de l’acidité et du degré d’oxydoréduction de l’eau de mer. C’est ce qu’on appelle la Grande oxydation ou la Catastrophe de l’oxygène. Vers -1.900 millions d’années, la presque totalité du fer présent dans les océans avait précipité et il se retrouve aujourd’hui dans les grands gisements de minerai mondiaux tels que ceux de Hamersley.
    [Show full text]
  • HIGH PRECISION ABUNDANCES of the OLD SOLAR TWIN HIP 102152: INSIGHTS on LI DEPLETION from the OLDEST SUN* Talawanda R
    Published in ApJL. Preprint typeset using LATEX style emulateapj v. 04/17/13 HIGH PRECISION ABUNDANCES OF THE OLD SOLAR TWIN HIP 102152: INSIGHTS ON LI DEPLETION FROM THE OLDEST SUN* TalaWanda R. Monroe1, Jorge Melendez´ 1, Ivan´ Ram´ırez2, David Yong3, Maria Bergemann4, Martin Asplund3, Jacob Bean5, Megan Bedell5, Marcelo Tucci Maia1, Karin Lind6, Alan Alves-Brito3, Luca Casagrande3, Matthieu Castro7, Jose{Dias´ do Nascimento7, Michael Bazot8, and Fabr´ıcio C. Freitas1 Published in ApJL. ABSTRACT We present the first detailed chemical abundance analysis of the old 8.2 Gyr solar twin, HIP 102152. We derive differential abundances of 21 elements relative to the Sun with precisions as high as 0.004 dex (.1%), using ultra high-resolution (R = 110,000), high S/N UVES spectra obtained on the 8.2-m Very Large Telescope. Our determined metallicity of HIP 102152 is [Fe/H] = -0.013 ± 0.004. The atmospheric parameters of the star were determined to be 54 K cooler than the Sun, 0.09 dex lower in surface gravity, and a microturbulence identical to our derived solar value. Elemental abundance ratios examined vs. dust condensation temperature reveal a solar abundance pattern for this star, in contrast to most solar twins. The abundance pattern of HIP 102152 appears to be the most similar to solar of any known solar twin. Abundances of the younger, 2.9 Gyr solar twin, 18 Sco, were also determined from UVES spectra to serve as a comparison for HIP 102152. The solar chemical pattern of HIP 102152 makes it a potential candidate to host terrestrial planets, which is reinforced by the lack of giant planets in its terrestrial planet region.
    [Show full text]
  • Astronomy 2008 Index
    Astronomy Magazine Article Title Index 10 rising stars of astronomy, 8:60–8:63 1.5 million galaxies revealed, 3:41–3:43 185 million years before the dinosaurs’ demise, did an asteroid nearly end life on Earth?, 4:34–4:39 A Aligned aurorae, 8:27 All about the Veil Nebula, 6:56–6:61 Amateur astronomy’s greatest generation, 8:68–8:71 Amateurs see fireballs from U.S. satellite kill, 7:24 Another Earth, 6:13 Another super-Earth discovered, 9:21 Antares gang, The, 7:18 Antimatter traced, 5:23 Are big-planet systems uncommon?, 10:23 Are super-sized Earths the new frontier?, 11:26–11:31 Are these space rocks from Mercury?, 11:32–11:37 Are we done yet?, 4:14 Are we looking for life in the right places?, 7:28–7:33 Ask the aliens, 3:12 Asteroid sleuths find the dino killer, 1:20 Astro-humiliation, 10:14 Astroimaging over ancient Greece, 12:64–12:69 Astronaut rescue rocket revs up, 11:22 Astronomers spy a giant particle accelerator in the sky, 5:21 Astronomers unearth a star’s death secrets, 10:18 Astronomers witness alien star flip-out, 6:27 Astronomy magazine’s first 35 years, 8:supplement Astronomy’s guide to Go-to telescopes, 10:supplement Auroral storm trigger confirmed, 11:18 B Backstage at Astronomy, 8:76–8:82 Basking in the Sun, 5:16 Biggest planet’s 5 deepest mysteries, The, 1:38–1:43 Binary pulsar test affirms relativity, 10:21 Binocular Telescope snaps first image, 6:21 Black hole sets a record, 2:20 Black holes wind up galaxy arms, 9:19 Brightest starburst galaxy discovered, 12:23 C Calling all space probes, 10:64–10:65 Calling on Cassiopeia, 11:76 Canada to launch new asteroid hunter, 11:19 Canada’s handy robot, 1:24 Cannibal next door, The, 3:38 Capture images of our local star, 4:66–4:67 Cassini confirms Titan lakes, 12:27 Cassini scopes Saturn’s two-toned moon, 1:25 Cassini “tastes” Enceladus’ plumes, 7:26 Cepheus’ fall delights, 10:85 Choose the dome that’s right for you, 5:70–5:71 Clearing the air about seeing vs.
    [Show full text]
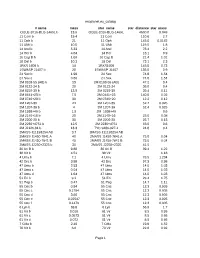
  • Exoplanet.Eu Catalog Page 1 # Name Mass Star Name
    exoplanet.eu_catalog # name mass star_name star_distance star_mass OGLE-2016-BLG-1469L b 13.6 OGLE-2016-BLG-1469L 4500.0 0.048 11 Com b 19.4 11 Com 110.6 2.7 11 Oph b 21 11 Oph 145.0 0.0162 11 UMi b 10.5 11 UMi 119.5 1.8 14 And b 5.33 14 And 76.4 2.2 14 Her b 4.64 14 Her 18.1 0.9 16 Cyg B b 1.68 16 Cyg B 21.4 1.01 18 Del b 10.3 18 Del 73.1 2.3 1RXS 1609 b 14 1RXS1609 145.0 0.73 1SWASP J1407 b 20 1SWASP J1407 133.0 0.9 24 Sex b 1.99 24 Sex 74.8 1.54 24 Sex c 0.86 24 Sex 74.8 1.54 2M 0103-55 (AB) b 13 2M 0103-55 (AB) 47.2 0.4 2M 0122-24 b 20 2M 0122-24 36.0 0.4 2M 0219-39 b 13.9 2M 0219-39 39.4 0.11 2M 0441+23 b 7.5 2M 0441+23 140.0 0.02 2M 0746+20 b 30 2M 0746+20 12.2 0.12 2M 1207-39 24 2M 1207-39 52.4 0.025 2M 1207-39 b 4 2M 1207-39 52.4 0.025 2M 1938+46 b 1.9 2M 1938+46 0.6 2M 2140+16 b 20 2M 2140+16 25.0 0.08 2M 2206-20 b 30 2M 2206-20 26.7 0.13 2M 2236+4751 b 12.5 2M 2236+4751 63.0 0.6 2M J2126-81 b 13.3 TYC 9486-927-1 24.8 0.4 2MASS J11193254 AB 3.7 2MASS J11193254 AB 2MASS J1450-7841 A 40 2MASS J1450-7841 A 75.0 0.04 2MASS J1450-7841 B 40 2MASS J1450-7841 B 75.0 0.04 2MASS J2250+2325 b 30 2MASS J2250+2325 41.5 30 Ari B b 9.88 30 Ari B 39.4 1.22 38 Vir b 4.51 38 Vir 1.18 4 Uma b 7.1 4 Uma 78.5 1.234 42 Dra b 3.88 42 Dra 97.3 0.98 47 Uma b 2.53 47 Uma 14.0 1.03 47 Uma c 0.54 47 Uma 14.0 1.03 47 Uma d 1.64 47 Uma 14.0 1.03 51 Eri b 9.1 51 Eri 29.4 1.75 51 Peg b 0.47 51 Peg 14.7 1.11 55 Cnc b 0.84 55 Cnc 12.3 0.905 55 Cnc c 0.1784 55 Cnc 12.3 0.905 55 Cnc d 3.86 55 Cnc 12.3 0.905 55 Cnc e 0.02547 55 Cnc 12.3 0.905 55 Cnc f 0.1479 55
    [Show full text]