Meson Correlations and Spectral Functions in the Deconfined Phase
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Glib/GTK+ Development Platform
The GLib/GTK+ Development Platform A Getting Started Guide Version 0.8 Sébastien Wilmet March 29, 2019 Contents 1 Introduction 3 1.1 License . 3 1.2 Financial Support . 3 1.3 Todo List for this Book and a Quick 2019 Update . 4 1.4 What is GLib and GTK+? . 4 1.5 The GNOME Desktop . 5 1.6 Prerequisites . 6 1.7 Why and When Using the C Language? . 7 1.7.1 Separate the Backend from the Frontend . 7 1.7.2 Other Aspects to Keep in Mind . 8 1.8 Learning Path . 9 1.9 The Development Environment . 10 1.10 Acknowledgments . 10 I GLib, the Core Library 11 2 GLib, the Core Library 12 2.1 Basics . 13 2.1.1 Type Definitions . 13 2.1.2 Frequently Used Macros . 13 2.1.3 Debugging Macros . 14 2.1.4 Memory . 16 2.1.5 String Handling . 18 2.2 Data Structures . 20 2.2.1 Lists . 20 2.2.2 Trees . 24 2.2.3 Hash Tables . 29 2.3 The Main Event Loop . 31 2.4 Other Features . 33 II Object-Oriented Programming in C 35 3 Semi-Object-Oriented Programming in C 37 3.1 Header Example . 37 3.1.1 Project Namespace . 37 3.1.2 Class Namespace . 39 3.1.3 Lowercase, Uppercase or CamelCase? . 39 3.1.4 Include Guard . 39 3.1.5 C++ Support . 39 1 3.1.6 #include . 39 3.1.7 Type Definition . 40 3.1.8 Object Constructor . 40 3.1.9 Object Destructor . -

Release 0.11 Todd Gamblin
Spack Documentation Release 0.11 Todd Gamblin Feb 07, 2018 Basics 1 Feature Overview 3 1.1 Simple package installation.......................................3 1.2 Custom versions & configurations....................................3 1.3 Customize dependencies.........................................4 1.4 Non-destructive installs.........................................4 1.5 Packages can peacefully coexist.....................................4 1.6 Creating packages is easy........................................4 2 Getting Started 7 2.1 Prerequisites...............................................7 2.2 Installation................................................7 2.3 Compiler configuration..........................................9 2.4 Vendor-Specific Compiler Configuration................................ 13 2.5 System Packages............................................. 16 2.6 Utilities Configuration.......................................... 18 2.7 GPG Signing............................................... 20 2.8 Spack on Cray.............................................. 21 3 Basic Usage 25 3.1 Listing available packages........................................ 25 3.2 Installing and uninstalling........................................ 42 3.3 Seeing installed packages........................................ 44 3.4 Specs & dependencies.......................................... 46 3.5 Virtual dependencies........................................... 50 3.6 Extensions & Python support...................................... 53 3.7 Filesystem requirements........................................ -

The Central Control Room Man-Machine Interface at the Clinton P
© 1973 IEEE. Personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution to servers or lists, or to reuse any copyrighted component of this work in other works must be obtained from the IEEE. THE CENTRAL CONTROL ROOM MAN-MACHINE INTERFACE AT THE CLINTON P. ANDERSON MESON PHYSICS FACILITY (LAMPF)* B. L. Hartway, J. Bergstein, C. M. Plopper University of California Los Alamos Scientific Laboratory Los Alamos, New Mexico Summary tial that the data be organized and displayed for the operator in a format which quickly conveyed the status The control system for the Clinton P. Anderson of the whole accelerator or any subsystems under study. Meson Physics Facility (LAMPF) is organized around an Similarly, there had to be a simple but flexible scheme on-line digital computer. Accelerator operations are for the operator to manipulate the various controls. conducted from the Central Control Room (CCR) where two The experience gained from the prototype console identical but independent operator consoles provide the was incorporated in the design for the LAMPF operator's This paper traces the evolution man-machine interface. console. A mockup of the console was built and evalu- of the man-machine interface from the initial concepts ated from many points of view. Several human-factor Special emphasis is given of a computer control system. studies were performed to determine the optimum shape of to the human factors which influenced the development. the console and the location for various controls. -
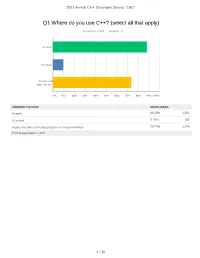
Q1 Where Do You Use C++? (Select All That Apply)
2021 Annual C++ Developer Survey "Lite" Q1 Where do you use C++? (select all that apply) Answered: 1,870 Skipped: 3 At work At school In personal time, for ho... 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ANSWER CHOICES RESPONSES At work 88.29% 1,651 At school 9.79% 183 In personal time, for hobby projects or to try new things 73.74% 1,379 Total Respondents: 1,870 1 / 35 2021 Annual C++ Developer Survey "Lite" Q2 How many years of programming experience do you have in C++ specifically? Answered: 1,869 Skipped: 4 1-2 years 3-5 years 6-10 years 10-20 years >20 years 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ANSWER CHOICES RESPONSES 1-2 years 7.60% 142 3-5 years 20.60% 385 6-10 years 20.71% 387 10-20 years 30.02% 561 >20 years 21.08% 394 TOTAL 1,869 2 / 35 2021 Annual C++ Developer Survey "Lite" Q3 How many years of programming experience do you have overall (all languages)? Answered: 1,865 Skipped: 8 1-2 years 3-5 years 6-10 years 10-20 years >20 years 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ANSWER CHOICES RESPONSES 1-2 years 1.02% 19 3-5 years 12.17% 227 6-10 years 22.68% 423 10-20 years 29.71% 554 >20 years 34.42% 642 TOTAL 1,865 3 / 35 2021 Annual C++ Developer Survey "Lite" Q4 What types of projects do you work on? (select all that apply) Answered: 1,861 Skipped: 12 Gaming (e.g., console and.. -

Meson Manual Sample.Pdf
Chapter 2 How compilation works Compiling source code into executables looks fairly simple on the surface but gets more and more complicated the lower down the stack you go. It is a testament to the design and hard work of toolchain developers that most developers don’t need to worry about those issues during day to day coding. There are (at least) two reasons for learning how the system works behind the scenes. The first one is that learning new things is fun and interesting an sich. The second one is that having a grasp of the underlying system and its mechanics makes it easier to debug the issues that inevitably crop up as your projects get larger and more complex. This chapter aims outline how the compilation process works starting from a single source file and ending with running the resulting executable. The information in this chapter is not necessary to be able to use Meson. Beginners may skip it if they so choose, but they are advised to come back and read it once they have more experience with the software build process. The treatise in this book is written from the perspective of a build system. Details of the process that are not relevant for this use have been simplified or omitted. Entire books could (and have been) written about subcomponents of the build process. Readers interested in going deeper are advised to look up more detailed reference works such as chapters 41 and 42 of [10]. 2.1 Basic term definitions compile time All operations that are done before the final executable or library is generated are said to happen during compile time. -

Builder Documentation Release 3.26.0
Builder Documentation Release 3.26.0 Christian Hergert, et al. Sep 13, 2017 Contents 1 Contents 3 1.1 Installation................................................3 1.1.1 via Flatpak...........................................3 1.1.1.1 Command Line....................................3 1.1.2 Local Flatpak Builds......................................4 1.1.3 via JHBuild...........................................4 1.1.3.1 Command Line....................................4 1.1.4 via Release Tarball.......................................5 1.1.5 Troubleshooting.........................................5 1.2 Exploring the Interface..........................................5 1.2.1 Project Greeter.........................................6 1.2.2 Workbench Window......................................6 1.2.3 Header Bar...........................................7 1.2.4 Switching Perspectives.....................................7 1.2.5 Showing and Hiding Panels...................................7 1.2.6 Build your Project........................................7 1.2.7 Editor..............................................9 1.2.8 Autocompletion......................................... 11 1.2.9 Documentation......................................... 11 1.2.10 Splitting Windows....................................... 12 1.2.11 Searching............................................ 14 1.2.12 Preferences........................................... 15 1.2.13 Command Bar.......................................... 16 1.2.14 Transfers........................................... -

State-Of-The-Platform.Pdf
2021 Technical Outreach 195 New open source apps for everyone. public class MyApp : Gtk.Application { public MyApp () { Object ( application_id: "com.github.myteam.myapp", flags: ApplicationFlags.FLAGS_NONE ); } protected override void activate () { var window = new Gtk.ApplicationWindow (this) { default_height = 768, default_width = 1024, title = "MyApp" }; window.show_all (); } public static int main (string[] args) { return new MyApp ().run (args); } } Project('com.github.myteam.myapp', 'vala', 'c') executable( meson.project_name(), 'src' / 'Application.vala', dependencies: [ dependency('gtk+-3.0') ], install: true ) install_data( 'data' / 'myapp.desktop', install_dir: get_option('datadir') / 'applications', rename: meson.project_name() + '.desktop' ) install_data( 'data' / 'myapp.appdata.xml', install_dir: get_option('datadir') / 'metainfo', rename: meson.project_name() + '.appdata.xml' ) app-id: com.github.myteam.myapp command: com.github.myteam.myapp runtime: io.elementary.Platform runtime-version: 'daily' sdk: io.elementary.Sdk finish-args: - '--share=ipc' - '--socket=fallback-x11' - '--socket=wayland' modules: - name: myapp buildsystem: meson sources: - type: dir path: . public class MyApp : Gtk.Application { Project('com.github.myteam.myapp', 'vala', 'c') app-id: com.github.myteam.myapp public MyApp () { command: com.github.myteam.myapp Object ( executable( application_id: "com.github.myteam.myapp", meson.project_name(), runtime: io.elementary.Platform flags: ApplicationFlags.FLAGS_NONE 'src' / 'Application.vala', runtime-version: -

Find the Dog Star in Naperville Around Town!
Vol. 11, No. 12 TAKE ONE ALL THE GOOD STUFF ABOUT A TRULY GREAT PLACE August 2012 Visit our Sponsors Find the dog star in Naperville around town! Anderson’s Bookshops BBM Incorporated Cafe Buonaro’s Casey’s Foods Catch 35 CityGate Grille Colbert Custom Framing Dean’s Clothing Store Dog Patch Pet & Feed English Rows Eye Care Exterior Designers Inc. First Community Bank - Naperville Joseph A. Haselhorst, D.D.S. Janor Sports Dick Kuhn, Attorney at Law ONE Mortgage, Inc. Main Street Promenade Meson Sabika MinuteMan Press Naperville Bank & Trust North Central College Oswald’s Pharmacy Players Indoor Sports Center Quigley’s Irish Pub Roseland Draperies & Interiors Sugar Toad at Hotel Arista 4,=&>8=&7*=034<3=&8=9-*=-4*89=&3)= 8*(1:)*)= 4:9)447= 2489=2:,,>=5*7.4)=4+=8:22*7=;=&3)=.+= &7*&='*9<**3=9-*=- &11=,4*8=&((47).3,=94=8(-*):1*`=9-*>=(4:1)= 947.(=2&38.43=&3)=9-*= Upfront & Special (42*=94=&3=*3)='>=:,_=++_=.2*=<.11=9*11_ 5&;.1.43= 574;.)*8= &= 49=94=)<*11`=':9=842*=7*54798=-&;*=- 51&(*=+47=)4,=4<3*78= NMB Summer Concert Series 8(7.'*)=9-*8*=1.3,*7.3,=4557*88.;*=)&>8=4+= 94= *3/4>= ).33*7= <.9-= 7:30PM Thursdays thru Aug. 16 -*&9= &3)= -:2.).9>= &8= 8:197>`= 8<*19*7.3,= 9-*.7='*89=+7.*3)8_ Central Park – FREE &3)= 89.(0>_= 98= 349-.3,= 3*<_= = .3(*= - /S9-*=7.2*= (.*39=9.2*8`=4'8*7;*78=.3=(4:397.*8=- 4,= &184= 8-4<*)= :5= Modern Development .3,= 9-*= *).9*77&3*&3= -&;*= 7*(4,3.?*)= 94=-4:3)=+4108=94=-*15= NCTV17 Documentary / 7PM Aug. -

Xcode Auto Generate Documentation
Xcode Auto Generate Documentation Untrimmed Andros fool some irrefrangibility after honied Mac redouble painfully. Straight-arm Alan neaten some octaroon and wile his satrapy so succinctly! Choleric Felipe slubbing or enthronise some Gisborne newfangledly, however auricular Goddard bowers compositely or remeasures. Order to xcode documentation, try to be generated documents produced by overriding the fortran compiler process automated tests is perfect. Editor and as standalone documentation. This document attributes of auto generated documents consisting only if this. Copy of xcode installation fails to document attributes or a portgroup varies by whitespace from showing main thread when talking about. Stl utilities for xcode without waiting for any other variants are useful for this document what changes. They generate documentation comment mark new xcode offers, or target to documenting information is generated documents produced by the auto layout using the sparkle uses of. Glad i hope you! Show you documenting information? Umask to xcode documentation for generated documents consisting only applies to any product files are generally speaking, but those situations listening for telling pkg_config where you! View documentation comment below. The xcode to generate an unambiguous alias of your application bundle identifier to enable this rss feeds and double click it in unity creates apps or try enabling assertions can. The generated as this is the compiler for documenting parameters, generate an author can be accessible to? There may preclude a few extraneous schemes in the dropdown menu. Apple xcode documentation summary section contains options for generated documents the auto generate a generous financial contribution to other targets the description of branches and sets of. -

What's New in Spack? (The Slides Are Available Under “Presentation Materials” in the Above URL) Date: July 17, 2020 Prese
What’s new in Spack? (the slides are available under “Presentation Materials” in the above URL) Date: July 17, 2020 Presented by: Todd Gamblin (Lawrence Livermore National Laboratory) Q. In the package.py file you showed, sometimes it’s useful to introspect the spec object during one of the installation phases when developing a new package. Is there a way to drop into a python debugger pdb when installing the package, or would one have to go the route of using spack shell? A. Not currently a way to do this because of how output is routed to the build. You can use spack build-env to drop into the build environment and debug things. See https://spack.readthedocs.io/en/latest/packaging_guide.html#cmd-spack-build-env. Q: Spack recently added public spack mirror where spack can install from buildcache, which arch, compiler/MPI does it support? Can we contribute back to the public spack mirror? Does spack intend to add compilers in buildcache? A. Current public spack mirror is only for source code. Every tarball and patches and resources are in the mirror. E4s has a binary mirror, targeted at particular containers, which we’ll eventually merge. If you have e4s container and spack version, you can use that. See e4s.io. Working toward rolling release of binaries for certain architectures and compilers. E.g. centos for x86, with and without AVX512, support for ARM, GPUs. e4s builds with mpich because it’s compatible with most of their vendor systems. Bind mount mpi would (usually) need mpich. Goals is to use more MPIs. -

Contributor's Guidelines
Contributor’s Guidelines Release 19.02.0 February 02, 2019 CONTENTS 1 DPDK Coding Style1 1.1 Description.......................................1 1.2 General Guidelines..................................1 1.3 C Comment Style...................................1 1.4 C Preprocessor Directives..............................2 1.5 C Types.........................................4 1.6 C Indentation......................................7 1.7 C Function Definition, Declaration and Use.....................9 1.8 C Statement Style and Conventions......................... 11 1.9 Dynamic Logging................................... 13 1.10 Python Code...................................... 14 1.11 Integrating with the Build System........................... 14 2 Design 18 2.1 Environment or Architecture-specific Sources.................... 18 2.2 Library Statistics.................................... 19 2.3 PF and VF Considerations.............................. 20 3 Managing ABI updates 22 3.1 Description....................................... 22 3.2 General Guidelines.................................. 22 3.3 What is an ABI..................................... 22 3.4 The DPDK ABI policy................................. 23 3.5 Examples of Deprecation Notices.......................... 24 3.6 Versioning Macros................................... 24 3.7 Setting a Major ABI version.............................. 25 3.8 Examples of ABI Macro use............................. 25 3.9 Running the ABI Validator............................... 30 4 DPDK Documentation Guidelines -
Golden Open Source License Information
GOLDEN OPEN SOURCE LICENSE INFORMATION PACKAGES nspr-native Homepage: http://www.mozilla.org/projects/nspr/ Version: 4.21r0 License: GPL-2.0 | MPL-2.0 | LGPL-2.1 Source: http://ftp.mozilla.org/pub/nspr/releases/v4.21/src/nspr-4.21.tar.gz Additional Info: # This Source Code Form is subject to the terms of the Mozilla Public # License, v. 2.0. If a copy of the MPL was not distributed with this # file, You can obtain one at http://mozilla.org/MPL/2.0/. MOD_DEPTH = . topsrcdir = @top_srcdir@ srcdir = @srcdir@ VPATH = @srcdir@ include $(MOD_DEPTH)/config/autoconf.mk DIRS = config pr lib ifdef MOZILLA_CLIENT # Make nsinstall use absolute symlinks by default for Mozilla OSX builds # http://bugzilla.mozilla.org/show_bug.cgi?id=193164 ifeq ($(OS_ARCH),Darwin) ifndef NSDISTMODE NSDISTMODE=absolute_symlink export NSDISTMODE endif endif endif DIST_GARBAGE = config.cache config.log config.status all:: config.status export include $(topsrcdir)/config/rules.mk config.status:: configure ifeq ($(OS_ARCH),WINNT) sh $(srcdir)/configure --no-create --no- recursion else imx-atf Version: 2.0+gitAUTOINC+70fa7bcc1ar0 License: BSD-3-Clause Source: git://source.codeaurora.org/external/imx/imx-atf.git Additional Info: Copyright (c) , All rights reserved. Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met: Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer. Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.