Exploring the Relationship Between Land Use/Land Cover Type And
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

(Asos) Implementation Plan
AUTOMATED SURFACE OBSERVING SYSTEM (ASOS) IMPLEMENTATION PLAN VAISALA CEILOMETER - CL31 November 14, 2008 U.S. Department of Commerce National Oceanic and Atmospheric Administration National Weather Service / Office of Operational Systems/Observing Systems Branch National Weather Service / Office of Science and Technology/Development Branch Table of Contents Section Page Executive Summary............................................................................ iii 1.0 Introduction ............................................................................... 1 1.1 Background.......................................................................... 1 1.2 Purpose................................................................................. 2 1.3 Scope.................................................................................... 2 1.4 Applicable Documents......................................................... 2 1.5 Points of Contact.................................................................. 4 2.0 Pre-Operational Implementation Activities ............................ 6 3.0 Operational Implementation Planning Activities ................... 6 3.1 Planning/Decision Activities ............................................... 7 3.2 Logistic Support Activities .................................................. 11 3.3 Configuration Management (CM) Activities....................... 12 3.4 Operational Support Activities ............................................ 12 4.0 Operational Implementation (OI) Activities ......................... -

2015 Indiana Airport Directory
Indiana Airport Directory CITY AIRPORT Alexandria Alexandria Airport Airport Manager Central Indiana Soaring Society Mr. David Colclasure (317) 373-6317 Business Business Address: 1577 E. 900 N. Alexandria, IN 46001 Email Address: [email protected] Airport President Central Indiana Soaring Society Mr. Tim Woenker Airport Vice President Central Indiana Soaring Society Mr. David Waymire Airport Secretary Central Indiana Soaring Society Mr. Scot Ortman Airport Treasurer Central Indiana Soaring Society Mr. Scot Ortman Internet Information Central Indiana Soaring Society Mr. David Waymire Email Address: [email protected] 9/1/2015 Indiana Department of Transportation Office of Aviation Page 1 of 116 Indiana Airport Directory Anderson Anderson Municipal Airport Airport Manager Mr. John Coon (765) 648-6293 Business (765) 648-6294 Fax Business Address: 282 Airport Road Anderson, IN 46017 Email Address: [email protected] Airport Board President Mr. Rodney French Airport Board Vice President Mr. Rick Senseney Airport Board Secretary Ms. Diana Brenneke Airport Board Member Mr. Steve Givens Airport Board Member Mr. David Albea Airport Consultant CHA, Companies Internet Information www.cityofanderson.com 9/1/2015 Indiana Department of Transportation, Office of Aviation Page 2 of 116 Indiana Airport Directory Angola Crooked Lake Seaplane Base Airport Manager Major Michael Portteus (317) 233-3847 Business (317) 232-8035 Fax (812) 837-9536 Dispatch Business Address: 402 W. Washington St. Rm W255D Indianapolis, IN 46204 Email Address: [email protected] Airport Owner Indiana Department of Natural Resources (317) 233-3847 Business (317) 232-8035 Fax Business Address: 402 W. Washington St. Room W255D Indianapolis, IN 46204 9/1/2015 Indiana Department of Transportation, Office of Aviation Page 3 of 116 Indiana Airport Directory Angola Lake James Seaplane Base Airport Manager Major Michael Portteus (317) 233-3847 Business (317) 232-8035 Fax (812) 837-9536 Dispatch Business Address: 402 W. -
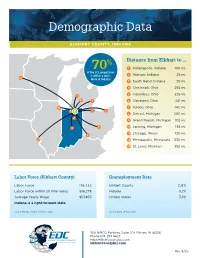
Demographic Data
Demographic Data ELKHART COUNTY, INDIANA % Distance from Elkhart to ... 1 Indianapolis, Indiana 150 mi. 70 of the U.S. population is within a day’s 2 Warsaw, Indiana 25 mi. 12 drive of Indiana 3 South Bend, Indiana 25 mi. 4 Cincinnati, Ohio 255 mi. 5 9 Columbus, Ohio 225 mi. 10 8 6 Cleveland, Ohio 241 mi. 11 7 Toledo, Ohio 140 mi. 3 E 7 6 8 Detroit, Michigan 200 mi. 2 9 Grand Rapids, Michigan 102 mi. 1 5 10 Lansing, Michigan 138 mi. 11 Chicago, Illinois 120 mi. 4 13 12 Minneapolis, Minnesota 530 mi. 13 St. Louis, Missouri 392 mi. Labor Force (Elkhart County) Unemployment Rate Labor Force 116,133 Elkhart County 2.8% Labor Force within 25 mile radius 616,278 Indiana 3.2% Average Yearly Wage $57,853 United States 3.5% Indiana is a right-to-work state Source: Bureau of Labor Statistics 2020 Source: DWD January 2020 300 NIBCO Parkway, Suite 201, Elkhart, IN 46516 Phone 574-293-5627 [email protected] elkhartcountybiz.com Rev 3/20 Demographic Data ELKHART COUNTY, INDIANA Commuting into Elkhart County Commuting out of Elkhart County 33,726 people live in another 8,491 people live in Elkhart county or state who commute County who commute to work to work into Elkhart County 19.3% outside the county 5.7% of the workforce of the workforce commutes into commutes out of Elkhart County Elkhart County MICHIGAN MICHIGAN 8,608 436 ST. JOSEPH LAGRANGE ST. JOSEPH LAGRANGE 11,863 E 3,436 4,581 E 782 MARSHALL OTHER STATES 1,657 (besides Michigan) KOSCIUSKO 1,657 KOSCIUSKO 4,249 936 Source: STATS Indiana Annual Commuiting Trends Profile Tax Year 2017 Source: STATS Indiana Annual Commuiting Trends Profile Tax Year 2017 Elkhart E Logistics Workforce County Interstate Access Proximity to Major Markets Advantages Low Taxes Low cost of Doing Business Major Manufacturers* Major Employers* Thor Industries, Inc. -

Higher Education and Continued Development Issue Control Medical Costs and Keep Employees Healthy
How to Train a Million People 34 | Safety Is Saving Us Money 56 | Hands on the Future 62 JANUARY/FEBRUARY 2018 CONNECTING FRONTLINE EXPERTS PROVOICES TO THE BUILDING INDIANA AUDIENCE HIGHER EDUCATION AND CONTINUED DEVELOPMENT ISSUE CONTROL MEDICAL COSTS AND KEEP EMPLOYEES HEALTHY A comprehensive approach to employers with job-related health needs OCCUPATIONAL HEALTH NEEDS MET WITH CONVENIENT HOURS IN MANY LOCATIONS Crown Point Portage Hammond Rensselaer Michigan City Valparaiso (866) 552-WELL (9355) 11/2017 REG17-29 Munster WorkingWell.org 2 www.BuildingIndiana.com | JANUARY/FEBRUARY 2018 WORKING LIKE A dog! DURING THE PANGERE CORPORATION BOARD MEETING, HOPE PANGERE HIGHLIGHTED A FEW 2017 MAJOR ACCOMPLISHMENTS: • One of 10 contractors • Recipient of the • 1,500 days without a lost nationwide and the Construction time workday FIRST ironworkers Advancement Foundation union contractor to 2017 Commercial earn AC478 Metal Contractor of the Year Building Assemblers Award and Commercial ACHIEVEMENTS Accreditation from Project of the Year Award SUCH AS THESE the International for the St. Catherine DEMONSTRATE Accreditation Service Hospital ICU Renovation PANGERE’S COMMITMENT TO CONTINUOUS IMPROVEMENT! 3 CommercialJANUARY/FEBRUARY and Industrial 2018 Construction | www.BuildingIndiana.com www.pangere.com Publisher’s Desk 219.226.0300 www.buildingindiana.com So Much to Learn! CORPORATE HEADQUARTERS 1330 Arrowhead Court Crown Point, IN 46307 We’re starting off 2018 with a whole new plan to continue delivering our readers the very best Indiana business news available. You may have already noticed a new look for our cover Publisher already, and there’s much more to come! Andrea M. Pearman Building Indiana is proud to be starting out a new chapter of its history this year with a [email protected] new series of articles called “Pro Voices.” In each issue, experts from Indiana industries that correspond to the overall issue’s theme will be selected to give their perspectives on topics that Sales John Brant impact companies throughout the state and beyond. -

A Summary of Cases June 19, 2020
A Summary of Cases June 19, 2020 PS19-0167 On May 3, 2019, the complainant contacted the Compliance Officer of the Office of Indiana State Chemist (OISC) to report an unknown pest management professional, possibly from Illinois, treated his duplex with a pesticide for the control of mold. The mold is still there, and the complainant does not believe the pest management professional is licensed. Disposition: A. Keith Hettich was cited for two (2) counts of violation of section 65(9) of the Indiana Pesticide Use and Application Law for applying pesticides for-hire without having an Indiana pesticide business license. A civil penalty in the amount of $500.00 (2 counts x $250.00 per count) was assessed. However, the civil penalty was reduced to $375.00. Consideration was given to the fact Keith Hettich cooperated during the investigation. B. As of November 26, 2019, Keith Hettich had not paid the $375.00 civil penalty assessed. A second letter was sent as a reminder the civil penalty was still owed to OISC. C. As of February 4, 2020, Keith Hettich had not paid the $375.00 civil penalty assessed. The case was forwarded to collections for the unmitigated civil penalty amount of $500.00. PS19-0169 On May 6, 2019, the complainant contacted the Compliance Officer of the Office of Indiana State Chemist (OISC) to report Jesse Lantz was making for-hire pesticide applications without being licensed. OISC database indicated Jesse Lantz was certified in category 7a but not licensed. Disposition: A. Jesse Lantz was cited for thirteen (13) counts of violation of section 65(9) of the Indiana Pesticide Use and Application Law for applying pesticides for hire without having an Indiana pesticide business license. -
SSSD Sites List 2018 01.Xlsx
January 2018_1 For SuperPack® licensors, Standard Site Settlement Data ("SSSD") is provided for no additional charge. These feeds do not require formal negotiation of specific Settlement Data contracts - the method used to generate Settlement Data under this service is defined in in the Standard Site Settlement Data Specfiction Neither Settlement Certificates nor Email Notifications are provided as standard under this service but may be requested for an additional administration charge. SSSD does not include the provision of feeds to counterparties. The list of Standard Sites is shown below and is subject to periodic updates ID Town WMO WBAN COOPID Country State Continent 57797 Aeroparque Bs. As. Aerodrome 87582 Argentina Distrito Federal South America 58961 Azul Aerodrome 87641 Argentina Buenos Aires South America 66589 Buenos Aires Observatorio 87585 Argentina Distrito Federal South America 57788 Ceres Aerodrome 87257 Argentina Santa Fe South America 58967 Comodoro Rivadavia Aerodrome 87860 Argentina Chubut South America 57790 Cordoba Aerodrome 87344 Argentina Cordoba South America 58970 Dolores Aerodrome 87648 Argentina Buenos Aires South America 58964 Ezeiza Aerodrome 87576 Argentina Buenos Aires South America 57787 Formosa Aerodrome 87162 Argentina Formosa South America 58973 Jujuy Aerodrome 87046 Argentina Jujuy South America 57796 Junin Aerodrome 87548 Argentina Buenos Aires South America 58977 Las Lomitas 87078 Argentina Formosa South America 57800 Mar Del Plata Aerodrome 87692 Argentina Buenos Aires South America 58979 Marcos -

KODY LOTNISK ICAO Niniejsze Zestawienie Zawiera 8372 Kody Lotnisk
KODY LOTNISK ICAO Niniejsze zestawienie zawiera 8372 kody lotnisk. Zestawienie uszeregowano: Kod ICAO = Nazwa portu lotniczego = Lokalizacja portu lotniczego AGAF=Afutara Airport=Afutara AGAR=Ulawa Airport=Arona, Ulawa Island AGAT=Uru Harbour=Atoifi, Malaita AGBA=Barakoma Airport=Barakoma AGBT=Batuna Airport=Batuna AGEV=Geva Airport=Geva AGGA=Auki Airport=Auki AGGB=Bellona/Anua Airport=Bellona/Anua AGGC=Choiseul Bay Airport=Choiseul Bay, Taro Island AGGD=Mbambanakira Airport=Mbambanakira AGGE=Balalae Airport=Shortland Island AGGF=Fera/Maringe Airport=Fera Island, Santa Isabel Island AGGG=Honiara FIR=Honiara, Guadalcanal AGGH=Honiara International Airport=Honiara, Guadalcanal AGGI=Babanakira Airport=Babanakira AGGJ=Avu Avu Airport=Avu Avu AGGK=Kirakira Airport=Kirakira AGGL=Santa Cruz/Graciosa Bay/Luova Airport=Santa Cruz/Graciosa Bay/Luova, Santa Cruz Island AGGM=Munda Airport=Munda, New Georgia Island AGGN=Nusatupe Airport=Gizo Island AGGO=Mono Airport=Mono Island AGGP=Marau Sound Airport=Marau Sound AGGQ=Ontong Java Airport=Ontong Java AGGR=Rennell/Tingoa Airport=Rennell/Tingoa, Rennell Island AGGS=Seghe Airport=Seghe AGGT=Santa Anna Airport=Santa Anna AGGU=Marau Airport=Marau AGGV=Suavanao Airport=Suavanao AGGY=Yandina Airport=Yandina AGIN=Isuna Heliport=Isuna AGKG=Kaghau Airport=Kaghau AGKU=Kukudu Airport=Kukudu AGOK=Gatokae Aerodrome=Gatokae AGRC=Ringi Cove Airport=Ringi Cove AGRM=Ramata Airport=Ramata ANYN=Nauru International Airport=Yaren (ICAO code formerly ANAU) AYBK=Buka Airport=Buka AYCH=Chimbu Airport=Kundiawa AYDU=Daru Airport=Daru -

Rules and Regulations Federal Register Vol
50605 Rules and Regulations Federal Register Vol. 81, No. 148 Tuesday, August 2, 2016 This section of the FEDERAL REGISTER adopting exemptions from the initial 1501 Farm Credit Drive, McLean, VA contains regulatory documents having general and variation margin requirements 22102–5090. applicability and legal effect, most of which published by the Agencies in November FHFA: George Sacco, Senior Financial are keyed to and codified in the Code of 2015 pursuant to sections 731 and 764 Analyst, Division of Housing Mission Federal Regulations, which is published under of the Dodd-Frank Wall Street Reform and Goals, (202) 649–3276, 50 titles pursuant to 44 U.S.C. 1510. and Consumer Protection Act (the [email protected], or Peggy K. The Code of Federal Regulations is sold by ‘‘Dodd-Frank Act’’ or the ‘‘Act’’). Balsawer, Associate General Counsel, the Superintendent of Documents. Prices of Pursuant to Title III of the Terrorism Office of General Counsel, (202) 649– new books are listed in the first FEDERAL Risk Insurance Program Reauthorization 3060, [email protected], Federal REGISTER issue of each week. Act of 2015 (‘‘TRIPRA’’), this final rule Housing Finance Agency, Constitution exempts certain non-cleared swaps and Center, 400 7th St. SW., Washington, DC non-cleared security-based swaps with 20219. The telephone number for the DEPARTMENT OF THE TREASURY certain financial and non-financial end Telecommunications Device for the users that qualify for an exception or Hearing Impaired is (800) 877–8339. Office of the Comptroller of the exemption from clearing. Currency SUPPLEMENTARY INFORMATION: DATES: This final rule is effective I. -

Vfr/Gps Chart Update
30 JUN 11 VFR ENROUTE CHANGE NOTICES US-1 VFR+GPS CHARTS NORTH AMERICA Jeppesen CHART CHANGE NOTICES highlight only significant changes affecting Jeppesen Charts, also regularly updated at www.jeppesen.com. IMPORTANT: CHECK FOR NOTAMS AND OTHER PERTINENT INFORMATION PRIOR TO FLIGHT. WAYPOINTS AND ROUTES VFR ENROUTE CHARTS NONE CHANGES TO LISTINGS ON THE REVERSE SIDE Cleveland-Hopkins Intl, CLE. Tower freq 124.50 MHz 06L/24R withdrawn. GENERAL NOTICES GL-2 New edition available from JUN 30 The Chart Change Notices are valid for the following Chart editions: AIRPORTS Great Lakes: Evart Mun, 9C8. Rwy length chgd to 3800‟. GL-1 (5th), GL-2 (5th), GL-3 (7th), GL-4 (4th), GL-5 (4th), Jasper Co, RZL. AWOS svc withdrawn. th th th th Kropf, 0II6. Apt perm withdrawn at N413835 W0854947. GL-6 (4 ), GL-7 (4 ), GL-8 (4 ), GL-9 (4 ) MC Helipad, 91MI. North Central: New civil Heliport estbld at N424456 W0852837. rd rd rd rd rd NC-1 (3 ), NC-2 (3 ), NC-3 (3 ), NC-4 (3 ), NC-5 (3 ), Podell, IN76. Apt perm withdrawn at N410735 W0864136. NC-6 (3rd), NC-7 (3rd), NC-8 (3rd), NC-9 (3rd), th rd rd th NC-10 (4 ), NC-11 (3 ), NC-12 (3 ), NC-13 (4 ), AIRSPACE th rd th th NC-14 (7 ), NC-15 (3 ), NC-16 (4 ), NC-17 (4 ), CLASS E Kokomo, IN. Modified. That airspace extending NC-18 (3rd), NC-19 (4th) upward from 700 feet above the surface within a 7 mile radius North East: of Kokomo Municipal Airport (N403141 W0860332). -
Final Documents/Your Two Cents—August 2016
Final Documents/Your Two Cents—August 2016 This list includes Federal Register (FR) publications such as rules, Advisory Circulars (ACs), policy statements and related material of interest to ARSA members. The date shown is the date of FR publication or other official release. Proposals opened for public comment represent your chance to provide input on rules and policies that will affect you. Agencies must provide the public notice and an opportunity for comment before their rules or policies change. Your input matters. Comments should be received before the indicated due date; however, agencies often consider comments they receive before drafting of the final document begins. Hyperlinks provided in blue text take you to the full document. If this link is broken, go to http://www.regulation.gov. In the keyword or ID field, type “FAA” followed by the docket number. August 1, 2016 FAA Guidance Documents and Notices FAA Final Advisory Circulars AC: Airport Field Condition Assessments and Winter Operations Safety Issued 07/29/2016 Document #: AC 150/5200- Effective date 10/01/2016 30D This AC provides guidance to assist airport operators in developing a snow and ice control plan, assessing and reporting airport conditions through the utilization of the Runway Condition Assessment Matrix (RCAM), and establishing snow removal and control procedures Flight Standards Information Management System (FSIMS) FSIMS: ED 1.4.2 145F AW Certificate Requirements Issued 07/13/2016 Revision 8, to keep OpSpecs, organizational charts, and capability lists up to date and available. FSIMS: ED 1.4.4 145G AW Quality Control System Issued 07/13/2016 Revision 11, to provide quality control of maintenance or alterations performed. -
![[4910-13] Department of Transportation](https://docslib.b-cdn.net/cover/4287/4910-13-department-of-transportation-6404287.webp)
[4910-13] Department of Transportation
This document is scheduled to be published in the Federal Register on 05/03/2016 and available online at http://federalregister.gov/a/2016-10177, and on FDsys.gov [4910-13] DEPARTMENT OF TRANSPORTATION Federal Aviation Administration 14 CFR Part 71 Docket No. FAA-2016-4291; Airspace Docket No. 16-AGL-7 Proposed Amendment of Class E Airspace for the following Indiana Towns; Goshen, IN; Greencastle, IN; Huntingburg, IN; North Vernon, IN; Rensselaer, IN; Tell City, IN; and Washington, IN; and Revocation of Class E Airspace; Vincennes, IN AGENCY: Federal Aviation Administration (FAA), DOT. ACTION: Notice of proposed rulemaking (NPRM). SUMMARY: This action proposes to modify Class E airspace extending upward from 700 feet above the surface at Vigil I. Grissom Municipal Airport, Bedford, IN; Goshen Municipal Airport, Goshen, IN; Putnam County Airport, Greencastle, IN; Huntingburg Airport, Huntingburg, IN; North Vernon Airport, North Vernon, IN; Jasper County Airport, Rensselaer, IN; Perry County Municipal Airport, Tell City, IN; and Daviess County Airport, Washington, IN. This action also proposes to remove Class E airspace extending upward from 700 feet above the surface at O’Neal Airport, Vincennes, IN. Decommissioning of non-directional radio beacons (NDB), cancellation of NDB approaches, implementation of area navigation (RNAV) procedures, and closure of O’Neal Airport, have made this action necessary for the safety and management of Instrument Flight Rules (IFR) operations at the above airports. This action also would update the geographic coordinates of Goshen Municipal Airport, Putnam County Airport, North Vernon Airport, Jasper County Airport, and Perry County Municipal Airport to coincide with the FAAs aeronautical database. -

Internally Managed Datasets Service Type Provider Description Variables
Internally Managed Datasets QC Validation checks QC Service Type provider description variables performed? Specific QC Validation performed by GLOS Partner Buoys Grand Valley State University Muskegon Lake Buoy (GVSU1) air pressure yes between 700-1200 mmHg GLOS air temperature yes between 0-50 deg C GLOS relative humidity yes between 0-100% GLOS water temperature (@0ft) yes between 0-40 deg C GLOS wind direction yes between 0-360 deg GLOS wind gust yes between 0-50 m/s GLOS wind speed yes between 0-50 m/s GLOS Illinois-Indiana Sea Grant and Illinios-Indiana Sea Grant Buoy between 0-15 sec Purdue Civil Engineering (45170) dominant wave period yes GLOS mean wave direction peak period yes between 0-15 sec GLOS significant wave height yes between 0-10 m GLOS water temperature yes between 0-40 deg C GLOS wind direction yes between 0-360 deg GLOS wind gust yes between 0-50 m/s GLOS wind speed yes between 0-50 m/s GLOS Wilmette Weather Buoy between 0-50 deg C (45174) air temperature yes GLOS dew point yes between -30 and 50 deg C GLOS significant wave height yes between 0-10 m GLOS significant wave period yes between 0-15 sec GLOS water temperature (@0ft) yes between 0-40 deg C GLOS wind direction yes between 0-360 deg GLOS wind gust yes between 0-50 m/s GLOS wind speed yes between 0-50 m/s GLOS Internally Managed Datasets QC Validation checks QC Service Type provider description variables performed? Specific QC Validation performed by Limno Tech Cook Plant Buoy (45026) air temperature yes between 0-50 deg C GLOS dew point yes between -30 and