Paris Case Study
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

DLA Piper. Details of the Member Entities of DLA Piper Are Available on the Website
EUROPEAN PPP REPORT 2009 ACKNOWLEDGEMENTS This Report has been published with particular thanks to: The EPEC Executive and in particular, Livia Dumitrescu, Goetz von Thadden, Mathieu Nemoz and Laura Potten. Those EPEC Members and EIB staff who commented on the country reports. Each of the contributors of a ‘View from a Country’. Line Markert and Mikkel Fritsch from Horten for assistance with the report on Denmark. Andrei Aganimov from Borenius & Kemppinen for assistance with the report on Finland. Maura Capoulas Santos and Alberto Galhardo Simões from Miranda Correia Amendoeira & Associados for assistance with the report on Portugal. Gustaf Reuterskiöld and Malin Cope from DLA Nordic for assistance with the report on Sweden. Infra-News for assistance generally and in particular with the project lists. All those members of DLA Piper who assisted with the preparation of the country reports and finally, Rosemary Bointon, Editor of the Report. Production of Report and Copyright This European PPP Report 2009 ( “Report”) has been produced and edited by DLA Piper*. DLA Piper acknowledges the contribution of the European PPP Expertise Centre (EPEC)** in the preparation of the Report. DLA Piper retains editorial responsibility for the Report. In contributing to the Report neither the European Investment Bank, EPEC, EPEC’s Members, nor any Contributor*** indicates or implies agreement with, or endorsement of, any part of the Report. This document is the copyright of DLA Piper and the Contributors. This document is confidential and personal to you. It is provided to you on the understanding that it is not to be re-used in any way, duplicated or distributed without the written consent of DLA Piper or the relevant Contributor. -

“10 out of TEN” TEN-T Project Implementation Successes
“10 OUT OF TEN” TEN-T Project Implementation Successes out 10 of TEN “10 OUT OF TEN” TEN-T Project Implementation Successes Project 9 Port enhancements out Page 10 of TEN 1-2-3-4-5-6-7-8-9-TEN: This brochure highlights 10 out of the 10 many implementation successes of the Trans-European Transport Project 1 Air traffic Network programme, for projects that the TEN-T Executive management Page 2 Agency is managing on behalf of the European Commission. The TEN-T programme plays a vital role in financing transport infrastructure by granting support to selected European projects Project 5 Project 2 ERTMS Motorway in all transport modes and in every EU Member State. With the installation connection Page 6 Page 3 ultimate aim of forming a multi-modal network that allows people Project 10 and goods to circulate quickly and easily in a single European ITS for roads transport area, TEN-T projects are also helping to build an integrated, Page 11 greener and ultimately decarbonised European transport system Project 3 Rail journey which benefits all EU citizens, both economically and socially. planning The TEN-T Executive Agency is playing its part by ensuring efficient Page 4 Project 7 and effective implementation of the projects. Inland waterways Page 8 As you journey through these pages, you will experience first- Project 4 hand how these individual TEN-T projects are collectively helping High-speed to complete the TEN-T network and change the face of European rail Page 5 mobility. Let's get moving… Project 6 High-speed Project 8 rail Inland waterways -
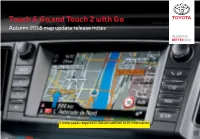
Touch & Go and Touch 2 with Go
Touch & Go and Touch 2 with Go Autumn 2018 map update release notes 4 more pages required in Autumn edition to fit information Keeping up to date with The Toyota Map Update Release Notes Map update information these and many more features: Touch & Go (CY11) helps you stay on track with the map Full map navigation Release date: Autumn 2018 Driver-friendly full map pan-European navigation updates of the Touch & Go and Touch 2 Version: 2018 with clear visual displays for signposts, junctions and lane with Go navigation systems. Database: 2018.Q1 guidance. Media: USB stick or download by user Speed limit and safety Toyota map updates are released at least once a year System vendor: Harman camera alerts Drive safely with the help of a and at a maximum twice. Coverage: Albania, Andorra, Austria, Belarus, Belgium, Bosnia Herzegovina, speed limit display and warning, including an optional Bulgaria, Croatia, Czech Republic, Denmark, Estonia, Finland, Gibraltar, France, speed warning setting. Alerts Keep up with the product information, map changes, Germany, Greece, Hungary, Iceland, Ireland, Italy, Kazakhstan, Kosovo, Latvia, notify you of fixed safety Liechtenstein, Lithuania, Luxembourg, Macedonia (F.Y.R.O.M), Malta, Moldova, camera locations (in countries premium content and sales arguments. where it is legal). Monaco, Montenegro, Netherlands, Norway, Poland, Portugal, Romania, Russia, San Marino, Serbia, Slovak Republic, Slovenia, Spain, Sweden, Switzerland, Turkey, Ukraine, United Kingdom, Vatican. Intuitive detour suggestions Real-time traffic information Contents updates* alert you to Touch 2 with Go (CY13/16) congestion ahead on your planned route. The system Map update information 3 Release date: Autumn, 2018 calculates potential delay times and suggests a detour Navigation features 4 Version: 2018 to avoid the problem. -

The Case of the World Cup 2006 in Germany
Working Paper Series, Paper No. 07-04 Relationships between investments costs for infrastructure and for sport stadia: The case of the World Cup 2006 in Germany Nicolas Büttner†,Wolfgang Maennig††, and Marco Messner††† April 2007 Abstract This study uses the example of the 2006 soccer World Cup in Germany to examine whether any systematic relationships exist between infrastructure investments on the one hand and investments in the respective stadium on the other. Particular attention is paid to an examination of whether the relative infrastructure costs in the case of newly-built stadia differ from those relating to stadia that have been reconstructed or extended. Such systematic relationships, or “rules of thumb”, could be used in the future to simplify the prediction of the expected volume of necessary infrastructure measures for major sporting events (other soccer World Cups, the Olympic Games, etc.) on the basis of the investment required for the sports venues. Our study makes use of a cluster and discriminance analysis and concludes that such general rules cannot be derived from the 2006 World Cup in Germany. JEL Classification Codes: L83, R42, R53 Keywords: Infrastructure investments, sport stadia costs, cluster analysis, discriminance analysis. This paper is also available as University of Hamburg Working Paper Series in Economic Policy, Number 04/2005 (revised 11/06). †University of Hamburg ††University of Hamburg, Chair for Economic Policy, Von-Melle-Park 5, 20146 Hamburg, Germany, E-mail: [email protected], phone: +49 (0)40 42838 - 4622, fax: +49 (0)40 42838 - 6251 (corresponding author) †††University of Hamburg Nicolas Büttner, Wolfgang Maennig∗, Marco Menßen Relationships between investments costs for infrastructure and for sport stadia: The case of the World Cup 2006 in Germany Abstract: This study uses the example of the 2006 soccer World Cup in Germany to examine whether any systematic relationships exist between infrastructure investments on the one hand and investments in the respective stadium on the other. -

Of Europe Beautiful
Beautiful ROADS of Europe I Beautiful ROADS of Europe Edited by Donaldas Andziulis Ex Arte | 2013 Vilnius II BEAUTIFUL ROADS OF EUROPE . Gritsun E hoto: hoto: UDK 625.7(4)(084) P Be28 Executive editor / compiler Donaldas Andziulis Editorial assistants Jayde Will, Marta Kuzmickaitė Designers Birutė Vilutienė, Ieva Kuzmienė Prepress Anatolij Kostrov Proof-reading Aingeal Flanagan All images in this book have been reproduced with the knowledge and prior consent of the individuals and organisations concerned. Every effort has been made to ensure that the credits accurately comply with the information supplied. © Ex Arte, 2013 ISBN 978-609-8010-24-4 First edition. Printed in Lithuania. The publishing of this book ‘Beautiful Roads of Europe’ is the name of this book. was funded by Here, the word ‘beautiful’ encompasses many things: aesthetic enjoyment, fantastic architecture, technical mastery, workmanship, road safety, and expanded trade. Have a pleasant journey on the beautiful roads of Europe! MA S I PR hoto: hoto: P Contents Roads of Europe – Benefits and challenges 6 NATIONAL ROAD NETWORKS Austria 12 Belgium 16 Cyprus 24 Denmark 28 Estonia 32 Finland 36 France 40 Germany 44 Greece 48 Hungary 52 Iceland 56 Ireland 60 Italy 64 Latvia 68 Lithuania 72 Luxembourg 76 Malta 80 Netherlands 84 Norway 88 Poland 92 Portugal 96 Romania 100 Slovenia 104 Spain 108 Sweden 112 Switzerland 116 United Kingdom 120 4 BEAUTIFUL ROADS OF EUROPE 5 Roads of Europe – Benefits and challenges Roads have been the lifeblood of our society since ancient times, whether for travel, trade, exploration, or conquest. The Silk Road from China to Europe, which is over 6,000 km long, has existed for more than 2,000 years. -

Paris Case Study
A cost-benefit analysis of tunnel † investment and tolling alternatives in Antwerp European Regional Science Association conference, Amsterdam, 2005 S. Proosta, S. Van der Loob, A. de Palmac, and R. Lindseyd Corresponding author: S. Proost ABSTRACT A proposal has been made to build a new tunnel under the Scheldt river near the centre of Antwerp in order to relieve traffic congestion on the ring road and in an existing tunnel. The new tunnel is expected to cost more than €1 billion, and tolls have been suggested to help finance construction and to manage demand. This paper conducts a preliminary cost-benefit analysis of a new tunnel and three alternative tolling schemes, and compares them with a do- nothing scenario and an option to toll the existing tunnel without building a new one. The analysis is performed using a model that was recently developed as part of the European- Union funded REVENUE project. The two tunnels are treated as imperfect substitutes, and a multi-year accounting framework is adopted that accounts for emissions, accidents and noise externalities, road damage, revenues accruing to the national and regional governments from existing transport user charges, and the salvage value of the new tunnel. With the base-case parameter values it is found that building the tunnel is worthwhile with all three tolling regimes and yields a higher benefit than not building the tunnel and tolling the old one. Nevertheless, the net benefit from building the tunnel differs appreciably between tolling regimes, and it is sensitive to the value assumed for the marginal cost of public funds. -

Road Pricing in Europe
1 ROAD PRICING IN EUROPE Second version April 2012 Colophon ROAD PRICING in EUROPE Issued by: RDW in cooperation with EReg Information: RDW-VIV2011/602 Date Updated: January 2012 Date Issued: April 2012 Version: Road Pricing in Europe version 2.0 Contact persons: Bertjan Marree en Melanie Meijer E-mail: [email protected] Design: Henk Kuipers This issue is also available in digital form on the EReg website, Association of European Vehicle and Driver Registration Authorities (www.ereg-association.eu). We are striving to continually improve this document, and therefore we would like to invite you to send any suggestions for improvements, additions, etc to us via e-mail ([email protected]) so that we are able to include this information in future versions. Copyright © 2012 by RDW All rights reserved No part of this book may be multiplied reproduces or made public, in any form bij print, photocopy, photo print, microfilm or any other means, without written permission from the RDW, Zoetermeer, the Netherlands, via e-mail: [email protected]. Road pricing in Europe 2 Road pricing in Europe 3 Content Foreword 5 1 Introduction 7 2 EETS 9 3 Austria 17 4 Belgium 29 5 Czech Republic 37 6 Denmark 49 7 Finland 55 8 France 61 9 Germany 69 10 Italy 79 11 Luxembourg 89 12 The Netherlands 93 13 Norway 99 14 Poland 109 15 Portugal 123 16 Spain 131 17 Sweden 137 18 Switzerland 147 19 United Kingdom 159 Abbreviations 169 Used literature 173 Notes 174 Road pricing in Europe 4 Road pricing in Europe 5 Foreword Toll collection is a fast growing business in Europe. -

1 Brisa – Concessão Rodoviária, SA (Incorporated
Brisa – Concessão Rodoviária, S.A. (incorporated with limited liability under the laws of Portugal) Euro 3,000,000,000 Euro Medium Term Note Programme Base Prospectus Under this Euro 3,000,000,000 Euro Medium Term Note Programme (the “Programme”), Brisa - Concessão Rodoviária, S.A. (the “Issuer” or “BCR”) may from time to time issue notes (the “Notes”) denominated in any currency agreed between the Issuer and the relevant Dealer or Dealers (as defined below) subject to applicable legal and regulatory central bank and securities authority requirements. The maximum aggregate nominal amount of all Notes from time to time outstanding under the Programme will not exceed Euro 3,000,000,000 (or its equivalent in other currencies calculated as described herein), subject to increase as described herein. Application has been made to the Commission de Surveillance du Secteur Financier (the “CSSF”) in its capacity as competent authority under the Luxembourg Act dated 10 July 2005 on prospectuses for securities (loi relative aux prospectus pour valeurs mobilières) to approve this document as a base prospectus in relation to the Issuer. The CSSF assumes no undertaking as to the economical and financial soundness of the information contained herein and the quality or solvency of the Issuer, pursuant to the provisions of article 7(7) of the Luxembourg Law dated 10 July 2005 on prospectuses for securities (implementing Directive 2003/71/EC of the European Parliament and of the Council of 4 November 2003 and amendments thereto, including Directive 2010/73/EU (the “Prospectus Directive”)). Application has also been made to the Luxembourg Stock Exchange for Notes issued under the Programme to be admitted to trading on the Bourse de Luxembourg, which is the regulated market of the Luxembourg Stock Exchange and to be listed on the Official List of the Luxembourg Stock Exchange. -

TEN – T Trans-European Transport Network
TEN – T Trans-European Transport Network Implementation of the Priority Projects Progress Report May 2008 Informal Transport Council Brdo, May 6, 2008 Information contained in this report summarises the current state of play regarding the development of the priority projects, including the sources of financing. It was put together with the data provided by the Member States in the framework of the annual survey on the implementation of priority project and complemented with information provided in response to the request of Vice President Barrot sent in preparation of the informal Council in Brdo. Each Member State provided information for the sections of the priority projects located on its territory, whereas the cross border sections were reported on jointly by the countries involved. In addition, the European Investment Bank provided information on the loans given to priority projects and the Commission added the figures reflecting the grant allocation to individual sections. This information was subsequently revised and in some cases altered by the Member States. Despite the attention given to the quality and reliability of data, some figures, especially on the sources of financing, may be missing. It should also be borne in mind that the data for the programming period 2007-2013 and beyond reflects intentions and plans of the Member States. In particular estimates of investment on TEN-T priority projects from cohesion policy funds are at this stage indicative. Information received may therefore naturally evolve in the future. The completeness of the information gathered in the table will be gradually improved since the process of data improvement based on further cooperation with Member States Authorities will continue. -

Public Private Partnership Options for the Second Generation of Motorway Developments in Poland
Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized PUBLIC PRIVATE PARTNERSHIP OPTIONS FOR THE SECOND GENERATION OF MOTORWAY DEVELOPMENTS IN POLAND Public Disclosure Authorized FINAL REPORT (cover image: by GDDKiA) INECO, S.A.; 2006 http://www.ineco.es Public Private Partnership Options for the Second Generation of Motorway Developments in Poland Final Report v. 1330 Project team: Team Leader: Antonio Lopez Corral Economist (National Accountancy Specialist): Antonio Sanchez Soliño Financial Specialist: Carlos Bonnelly Ginebra Institutional reinforcement and project evaluation specialist: Samuel Carpintero Legal Specialist: Alberto Ruiz Ojeda Local Specialist: Jakub Nalazek Local Specialist: Victoriano Sanz Losada CONTENTS Abbreviations ............................................................................................................................ 6 INTRODUCTION................................................................................................................................. 8 I. REVIEW AND ANALYSIS OF PAST EXPERIENCE.............................................................. 13 I.1. Road network planning, project programming and preparation ................................... 14 I.1.1. Basic legal and institutional framework............................................................ 14 I.1.2. Road planning and programming..................................................................... 18 I.1.3. European Union incidence in road planning and programming...................... -

North Sea-Baltic TEN-T Core Network Corridor – Project List, 14/07/2017
North Sea-Baltic TEN-T Core Network Corridor – Project list, 14/07/2017 Disclaimer: this list is indicative work in progress still evolving and does not represent a commitment by the MS or the project promoter. Project name Project category Project promoter Member States / Total costs (estimate, Project end date countries involved M EUR) Diabolo project Airport Infrabel BE 64.00 01/12/2023 Rail connection of the future Liège- Carex terminal and adaptation of Infrabel Rail BE unknown unknown existing HSL to allow the Liège Carex circulation of high- speed freight Iron Rhine: infrastructure works Rail Infrabel BE unknown unknown Brussels-Antwerp axis including the by-pass of Mechelen (1) L25: by-pass of Mechelen (2) Complex of otterbeek Rail Infrabel BE 144.4 01/12/2024 (3) HSL Vilvoorde - Antwerpen Albertkanaal (4) L25: adaptation of the track alignment in Duffel C-ITS for Trucks (CITRUS) Road Be-Mobile NV BE 1.82 01/09/2019 Flemish Department of C-Roads Belgium/Flanders Road Mobility and Public Works BE 3.18 01/12/2020 (MOW) Connecting Brussels airport Airport De Lijn BE 88.86 unknown OPTI CONNECT Maritime NV ITC Rubis Terminal BE 15.00 unknown Antwerp Vopak Chemical Terminals More Liguid Bulk 4 Rail Maritime BE 8.01 unknown Belgium NV ANTwerp Waterbus Exploration and Realisation Park&Ride building IWW Stad Antwerpen BE 16.58 unknown (ANTWERP) INtoLNG - Innovative LNG solutions Engie LNG Solutions Innovation BE 19.34 unknown to provide clean transport fuel Antwerp bvba Pilot deployment of a smart (bio-) Innovation DRIVE SYSTEMS BE 2.93