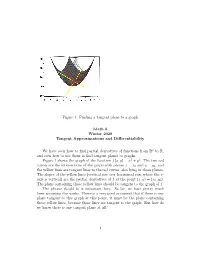
Vertical tangent
Top View
- Implicit Differentiation Investigations
- CALCULUS Table of Contents Calculus I, First Semester Chapter 1
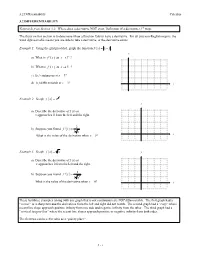
- §2.1—Limits, Rates of Change, and Tangent Lines
- Tangents of Parametric Curves
- Contemporarycalculuspart1.Pdf
- Concavity, Inflections, Cusps, Tangents, and Asymptotes
- Continuity Def: a Function F(X) Is Continuous at X = a If the Following Three Condi- Tions All Hold: (1) F(A) Exists (2) Lim F(X) Exists X→A (3) Lim F(X) = F(A)
- Continuity and Differentiability
- Derivatives Using Limits, We Can Define the Slope of a Tangent Line to a Function. When Given a Function F(X)
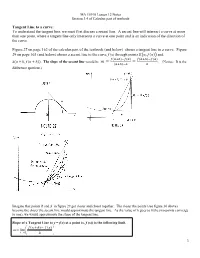
- §10.4 the Derivative Difference Quotient: Slope
- Parametric Equations and Polar Coordinates
- Math 124 Professor Christopher Hoffman Math 124
- Differentiability Versus Continuity: Restriction and Extension Theorems and Monstrous Examples
- Derivatives and Tangent Lines