DOCSLIB.ORG

Difference Quotients) 1.10.1

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Difference Quotients) 1.10.1 (Section 1.10: Difference Quotients) 1.10.1 SECTION 1.10: DIFFERENCE QUOTIENTS LEARNING OBJECTIVES • Define average rate of change (and average velocity) algebraically and graphically. • Be able to identify, construct, and evaluate (and simplify) various forms of difference quotients. PART A: DISCUSSION • This section will revisit Section 0.14 on slopes of lines, Section 1.1 on function evaluations, and Section 1.2 on graphs. • A difference quotient is used to find the slope of a secant line to a graph or to find an average rate of change (perhaps an average velocity). Difference quotients will form the basis for derivatives, tangent lines, and instantaneous rates of change in Section 1.11. PART B: SECANT LINES and AVERAGE RATE OF CHANGE The secant line to the graph of a function f on the interval a, b , where a < b, is the line that passes through the points ()a, fa() and ()b, fb(). The average rate of change of f on a, b is equal to the slope of this secant line, rise fb() fa() which is given by: = . run b a difference of outputs We call this a difference quotient, because it has the form: . difference of inputs • (See Footnote 1 on assumptions about f .) (Section 1.10: Difference Quotients) 1.10.2 PART C: AVERAGE VELOCITY The following development of average velocity will help explain the association between slope and average rate of change. Example 1 (Average Velocity) A car is driven due north 100 miles during a two-hour trip. What is the average velocity of the car? • Let t = the time (in hours) elapsed since the beginning of the trip. • Let y = st, where s is the position function for the car (in miles). () s gives the signed distance of the car from the starting position. •• The position (s) values would be negative if the car were south of the starting position. • Let s 0 = 0, meaning that y = 0 corresponds to the starting position. () Therefore, s 2 = 100 (miles). () The average velocity on the time-interval a, b is the average rate of change of position with respect to time. That is, change in position s = change in time t where (uppercase delta) denotes “change in” sb() sa() = , a difference quotient b a Here, the average velocity on 0, 2 is: s()2 s()0 100 0 = 2 0 2 miles mi = 50 or or mph hour hr unit of s TIP 1: The unit of velocity is the unit of slope given by: . unit of t (Section 1.10: Difference Quotients) 1.10.3 The average velocity is 50 mph on 0, 2 in the three scenarios below. It is the slope of the orange secant line. We will define instantaneous velocity (or simply velocity) in Section 1.11. • Here, the velocity is constant (50 mph). • Here, the velocity is increasing; the car is accelerating. • Here, the car overshoots the destination and then backtracks. WARNING 1: The car’s velocity is negative in value when it is backtracking; this happens when the graph falls. • In calculus, the Mean Value Theorem for Derivatives will imply that the car must be going exactly 50 mph at some time value t in 0, 2 . The theorem applies in all three () scenarios above, because s is continuous on 0, 2 and is differentiable on 0, 2 , () meaning that its graph makes no sharp turns and does not exhibit “infinite steepness” on ()0, 2 . Differentiability will be discussed in Section 1.11. § (Section 1.10: Difference Quotients) 1.10.4 PART D: FORMS OF DIFFERENCE QUOTIENTS The purposes of these forms will be discussed in Section 1.11 on derivatives. Forms of Difference Quotients Form 1: Fixed interval fb() fa() a, b are constants b a Form 2: Variable endpoint (x) fx() fa() a is constant; x is variable x a Form 3: Variable run (h) fa()+ h fa() a is constant; h is variable h Form 4: Variable endpoint (x) and Variable run (h) fx()+ h fx() x, h are variable h • The denominators can be negative. (See Footnote 2 in Section 1.11.) (Section 1.10: Difference Quotients) 1.10.5 PART E: EVALUATING DIFFERENCE QUOTIENTS Example 2 (Form 1 of a Difference Quotient; Profit) A company sells widgets. Assume that all widgets produced are sold. Let P be the profit function for the company; Px() is the profit (in dollars) if x widgets are produced and sold. Our model: Px= x2 + 200x 5000. () Find the average rate of change of profit between 60 and 90 widgets. WARNING 2: We will treat the domain of P as 0, ), even though one could argue that the domain should only consist of integers. Be aware of this issue with applications such as these. § Solution 2 2 90 + 200 90 5000 60 + 200 60 5000 P()90 P()60 () () () () = 90 60 30 WARNING 3: Grouping symbols are essential when expanding P 60 here, since we are subtracting an () expression with more than one term. 8100 + 18,000 5000 3600 + 12,000 5000 = 30 8100 + 18,000 5000 + 3600 12,000 + 5000 = 30 TIP 2: Instead of completely evaluating P()90 and P()60 , it may help to take advantage of cancellations such as the one above. 1500 = 30 dollars = 50 widget (Section 1.10: Difference Quotients) 1.10.6 • The practical interpretation is that, if the company increases its production level from 60 widgets to 90 widgets, then its profit will increase by dollars 50 , on average. widget • The total increase in profit is $1500 over the 30 additional widgets. • The graph of y = Px is below. () dollars •• The slope of the orange secant line is also 50 . widget •• The fact that the slope is positive reflects the fact that the profit function is increasing on 60, 90 . We will revisit this idea in Section 1.11 on derivatives. § (Section 1.10: Difference Quotients) 1.10.7 Example 3 (Form 2 of a Difference Quotient; Revisiting Example 2 on Profit) Px P 60 2 () () Again, Px()= x + 200x 5000. Evaluate . (Form 2) x 60 § Solution 2 x2 + 200x 5000 60 + 200 60 5000 Px() P()60 () () = x 60 x 60 2 x + 200x 5000 3600 + 12,000 5000 = x 60 x2 + 200x 5000 + 3600 12,000 + 5000 = x 60 x2 + 200x 8400 = x 60 ()x2 200x + 8400 = x 60 • The Factor Theorem in Chapter 2 will imply that, if P is polynomial, then x 60 is a factor of the () numerator, which is equivalent to Px() P()60 . This is because 60 is a zero of the numerator: P()60 P()60 = 0 . ()x 60 ()x 140 = , ()x 60 ()x 60 1 = ()x 140 , ()x 60 = 140 x, x 60 () (Section 1.10: Difference Quotients) 1.10.8 dollars • The unit for the difference quotient is still , though we tend to omit widget it when a variable is present in our final expression. dollars • If we substitute x = 90 , we obtain 50 , our answer to Example 2. widget § (Section 1.10: Difference Quotients) 1.10.9 Example 4 (Form 3 of a Difference Quotient; Revisiting Example 2 on Profit) P 60 h P 60 2 ()+ () Again, Px()= x + 200x 5000. Evaluate . (Form 3) h § Solution P()60 + h P()60 h 2 2 60 + h + 200 60 + h 5000 60 + 200 60 5000 () () () () = h 2 ()3600 + 120h + h + 12,000 + 200h 5000 3600 + 12,000 5000 = h 3600 120h h2 + 12,000 + 200h 5000 + 3600 12,000 + 5000 = h 80h h2 = h h ()80 h = , ()h 0 h 1 = 80 h, h 0 () • If we substitute h = 30 , which corresponds to x = 90 , we obtain dollars 50 , our answer to Example 2. § widget (Section 1.10: Difference Quotients) 1.10.10 Example 5 (Form 4 of a Difference Quotient; Revisiting Example 2 on Profit) Px h Px 2 ()+ () Again, Px()= x + 200x 5000. Evaluate . (Form 4) h § Solution Px()+ h Px() h 2 x + h + 200 x + h 5000 x2 + 200x 5000 () () = h 2 2 2 ()x + 2xh + h + 200x + 200h 5000 x + 200x 5000 = h x2 2xh h2 + 200x + 200h 5000 x2 + 200x 5000 = h x2 2xh h2 + 200x + 200h 5000 + x2 200x + 5000 = h 2xh h2 + 200h = h h () 2x h + 200 = , ()h 0 h 1 = 2x h + 200, ()h 0 • If we substitute x = 60 and h = 30 (which then corresponds to x = 90 ), dollars we obtain 50 , our answer to Example 2. § widget (Section 1.10: Difference Quotients) 1.10.11 FOOTNOTES 1. Assumptions made about a function. When defining the average rate of change of a function f on an interval a, b , where a < b, sources typically do not state the assumptions fb() fa() made about f . The formula seems only to require the existence of fa() and b a fb, but we typically assume more than just that. () • Although the slope of the secant line on a, b can still be defined, we need more for the existence of derivatives (i.e., the differentiability of f ) and the existence of non-vertical tangent lines, as we will see in Section 1.11. • We ordinarily assume that f is continuous on a, b . Then, there are no holes, jumps, or vertical asymptotes on a, b when f is graphed. (See Section 1.5.) • We may also assume that f is differentiable on a, b . Then, the graph of f makes no sharp turns and does not exhibit “infinite steepness” (corresponding to vertical tangent lines). However, this assumption may lead to circular reasoning, because the ideas of secant lines and average rate of change are used to develop the ideas of derivatives, tangent lines, and instantaneous rate of change, as we will see in Section 1.11.
Load more

Recommended publications
  • Numerical Differentiation and Integration
    Chapter 4 Numerical Di↵erentiation and Integration 4.1 Numerical Di↵erentiation In this section, we introduce how to numerically calculate the derivative of a function. First, the derivative of the function f at x0 is defined as f x0 h f x0 f 1 x0 : lim p ` q´ p q. p q “ h 0 h Ñ This formula gives an obvious way to generate an approximation to f x0 : simply compute 1p q f x0 h f x0 p ` q´ p q h for small values of h. Although this way may be obvious, it is not very successful, due to our old nemesis round-o↵error. But it is certainly a place to start. 2 To approximate f x0 , suppose that x0 a, b ,wheref C a, b , and that x1 x0 h for 1p q Pp q P r s “ ` some h 0 that is sufficiently small to ensure that x1 a, b . We construct the first Lagrange ‰ Pr s polynomial P0,1 x for f determined by x0 and x1, with its error term: p q x x0 x x1 f x P0,1 x p ´ qp ´ qf 2 ⇠ x p q“ p q` 2! p p qq f x0 x x0 h f x0 h x x0 x x0 x x0 h p qp ´ ´ q p ` qp ´ q p ´ qp ´ ´ qf 2 ⇠ x “ h ` h ` 2 p p qq ´ for some ⇠ x between x0 and x1. Di↵erentiating gives p q f x0 h f x0 x x0 x x0 h f 1 x p ` q´ p q Dx p ´ qp ´ ´ qf 2 ⇠ x p q“ h ` 2 p p qq „ ⇢ f x0 h f x0 2 x x0 h p ` q´ p q p ´ q´ f 2 ⇠ x “ h ` 2 p p qq x x0 x x0 h p ´ qp ´ ´ qDx f 2 ⇠ x .
    [Show full text]
  • MPI - Lecture 11
    MPI - Lecture 11 Outline • Smooth optimization – Optimization methods overview – Smooth optimization methods • Numerical differentiation – Introduction and motivation – Newton’s difference quotient Smooth optimization Optimization methods overview Examples of op- timization in IT • Clustering • Classification • Model fitting • Recommender systems • ... Optimization methods Optimization methods can be: 1 2 1. discrete, when the support is made of several disconnected pieces (usu- ally finite); 2. smooth, when the support is connected (we have a derivative). They are further distinguished based on how the method calculates a so- lution: 1. direct, a finite numeber of steps; 2. iterative, the solution is the limit of some approximate results; 3. heuristic, methods quickly producing a solution that may not be opti- mal. Methods are also classified based on randomness: 1. deterministic; 2. stochastic, e.g., evolution, genetic algorithms, . 3 Smooth optimization methods Gradient de- scent methods n Goal: find local minima of f : Df → R, with Df ⊂ R . We assume that f, its first and second derivatives exist and are continuous on Df . We shall describe an iterative deterministic method from the family of descent methods. Descent method - general idea (1) Let x ∈ Df . We shall construct a sequence x(k), with k = 1, 2,..., such that x(k+1) = x(k) + t(k)∆x(k), where ∆x(k) is a suitable vector (in the direction of the descent) and t(k) is the length of the so-called step. Our goal is to have fx(k+1) < fx(k), except when x(k) is already a point of local minimum. Descent method - algorithm overview Let x ∈ Df .
    [Show full text]
  • Calculus Lab 4—Difference Quotients and Derivatives (Edited from U. Of
    Calculus Lab 4—Difference Quotients and Derivatives (edited from U. of Alberta) Objective: To compute difference quotients and derivatives of expressions and functions. Recall Plotting Commands: plot({expr1,expr2},x=a..b); Plots two Maple expressions on one set of axes. plot({f,g},a..b); Plots two Maple functions on one set of axes. plot({f(x),g(x)},x=a..b); This allows us to plot the Maple functions f and g using the form of plot() command appropriate to Maple expressions. If f and g are Maple functions, then f(x) and g(x) are the corresponding Maple expressions. The output of this plot() command is precisely the same as that of the preceding (function version) plot() command. 1. We begin by using Maple to compute difference quotients and, from them, derivatives. Try the following sequence of commands: 1 f:=x->1/(x^2-2*x+2); This defines the function f (x) = . x 2 − 2x + 2 (f(2+h)-f(2))/h; This is the difference quotient of f at the point x = 2. simplify(%); Simplifies the last expression. limit(%,h=0); This gives the derivative of f at the point where x = 2. Exercise 1: Find the difference quotient and derivative of this function at a general point x (hint: make a simple modification of the above steps). This f (x + h) − f (x) means find and f’(x). Record your answers below. h Use this to evaluate the derivative at the points x = -1 and x = 4. (It may help to remember the subs() command here; for example, subs(x=1,e1); means substitute x = 1 into the expression e1).
    [Show full text]
  • 3.2 the Derivative As a Function 201
    SECT ION 3.2 The Derivative as a Function 201 SOLUTION Figure (A) satisfies the inequality f .a h/ f .a h/ f .a h/ f .a/ C C 2h h since in this graph the symmetric difference quotient has a larger negative slope than the ordinary right difference quotient. [In figure (B), the symmetric difference quotient has a larger positive slope than the ordinary right difference quotient and therefore does not satisfy the stated inequality.] 75. Show that if f .x/ is a quadratic polynomial, then the SDQ at x a (for any h 0) is equal to f 0.a/ . Explain the graphical meaning of this result. D ¤ SOLUTION Let f .x/ px 2 qx r be a quadratic polynomial. We compute the SDQ at x a. D C C D f .a h/ f .a h/ p.a h/ 2 q.a h/ r .p.a h/ 2 q.a h/ r/ C C C C C C C 2h D 2h pa2 2pah ph 2 qa qh r pa 2 2pah ph 2 qa qh r C C C C C C C D 2h 4pah 2qh 2h.2pa q/ C C 2pa q D 2h D 2h D C Since this doesn’t depend on h, the limit, which is equal to f 0.a/ , is also 2pa q. Graphically, this result tells us that the secant line to a parabola passing through points chosen symmetrically about x a is alwaysC parallel to the tangent line at x a. D D 76. Let f .x/ x 2.
    [Show full text]
  • CHAPTER 3: Derivatives
    CHAPTER 3: Derivatives 3.1: Derivatives, Tangent Lines, and Rates of Change 3.2: Derivative Functions and Differentiability 3.3: Techniques of Differentiation 3.4: Derivatives of Trigonometric Functions 3.5: Differentials and Linearization of Functions 3.6: Chain Rule 3.7: Implicit Differentiation 3.8: Related Rates • Derivatives represent slopes of tangent lines and rates of change (such as velocity). • In this chapter, we will define derivatives and derivative functions using limits. • We will develop short cut techniques for finding derivatives. • Tangent lines correspond to local linear approximations of functions. • Implicit differentiation is a technique used in applied related rates problems. (Section 3.1: Derivatives, Tangent Lines, and Rates of Change) 3.1.1 SECTION 3.1: DERIVATIVES, TANGENT LINES, AND RATES OF CHANGE LEARNING OBJECTIVES • Relate difference quotients to slopes of secant lines and average rates of change. • Know, understand, and apply the Limit Definition of the Derivative at a Point. • Relate derivatives to slopes of tangent lines and instantaneous rates of change. • Relate opposite reciprocals of derivatives to slopes of normal lines. PART A: SECANT LINES • For now, assume that f is a polynomial function of x. (We will relax this assumption in Part B.) Assume that a is a constant. • Temporarily fix an arbitrary real value of x. (By “arbitrary,” we mean that any real value will do). Later, instead of thinking of x as a fixed (or single) value, we will think of it as a “moving” or “varying” variable that can take on different values. The secant line to the graph of f on the interval []a, x , where a < x , is the line that passes through the points a, fa and x, fx.
    [Show full text]
  • Differentiation
    CHAPTER 3 Differentiation 3.1 Definition of the Derivative Preliminary Questions 1. What are the two ways of writing the difference quotient? 2. Explain in words what the difference quotient represents. In Questions 3–5, f (x) is an arbitrary function. 3. What does the following quantity represent in terms of the graph of f (x)? f (8) − f (3) 8 − 3 4. For which value of x is f (x) − f (3) f (7) − f (3) = ? x − 3 4 5. For which value of h is f (2 + h) − f (2) f (4) − f (2) = ? h 4 − 2 6. To which derivative is the quantity ( π + . ) − tan 4 00001 1 .00001 a good approximation? 7. What is the equation of the tangent line to the graph at x = 3 of a function f (x) such that f (3) = 5and f (3) = 2? In Questions 8–10, let f (x) = x 2. 1 2 Chapter 3 Differentiation 8. The expression f (7) − f (5) 7 − 5 is the slope of the secant line through two points P and Q on the graph of f (x).Whatare the coordinates of P and Q? 9. For which value of h is the expression f (5 + h) − f (5) h equal to the slope of the secant line between the points P and Q in Question 8? 10. For which value of h is the expression f (3 + h) − f (3) h equal to the slope of the secant line between the points (3, 9) and (5, 25) on the graph of f (x)? Exercises 1.
    [Show full text]
  • CALCULUS I §2.2: Differentiability, Graphs, and Higher Derivatives
    MATH 12002 - CALCULUS I x2.2: Differentiability, Graphs, and Higher Derivatives Professor Donald L. White Department of Mathematical Sciences Kent State University D.L. White (Kent State University) 1 / 10 Differentiability The process of finding a derivative is called differentiation, and we define: Definition Let y = f (x) be a function and let a be a number. We say f is differentiable at x = a if f 0(a) exists. What does this mean in terms of the graph of f ? If f 0(a) = lim f (a+h)−f (a) exists, then f (a) must be defined. h!0 h Since the denominator is approaching 0, in order for the limit to exist, the numerator must also approach 0; that is, lim (f (a + h) − f (a)) = 0: h!0 Hence lim f (a + h) = f (a), and so lim f (x) = f (a), h!0 x!a meaning f must be continuous at x = a. D.L. White (Kent State University) 2 / 10 Differentiability But being continuous at a is not enough to make f differentiable at a. Differentiability is \continuity plus." The \plus" is smoothness: the graph cannot have a sharp \corner" at a. The graph also cannot have a vertical tangent line at x = a: the slope of a vertical line is not a real number. Hence, in order for f to be differentiable at a, the graph of f must 1 be continuous at a, 2 be smooth at a, i.e., no sharp corners, and 3 not have a vertical tangent line at x = a.
    [Show full text]
  • Example: Using the Grid Provided, Graph the Function
    3.2 Differentiability Calculus 3.2 DIFFERENTIABILITY Notecards from Section 3.2: Where does a derivative NOT exist, Definition of a derivative (3rd way). The focus on this section is to determine when a function fails to have a derivative. For all you non-English majors, the word differentiable means you are able to take a derivative, or the derivative exists. Example 1: Using the grid provided, graph the function fx( ) = x − 3 . y a) What is fx'( ) as x → 3− ? b) What is fx'( ) as x → 3+ ? c) Is f continuous at x = 3? d) Is f differentiable at x = 3? x 2 Example 2: Graph fx x3 y a) Describe the derivative of f (x) as x approaches 0 from the left and the right. 2 b) Suppose you found fx' . 33 x x What is the value of the derivative when x = 0? 3 Example 3: Graph fx x y a) Describe the derivative of f (x) as x approaches 0 from the left and the right. 1 b) Suppose you found fx' . 33 x2 What is the value of the derivative when x = 0? x These last three examples (along with any graph that is not continuous) are NOT differentiable. The first graph had a “corner” or a sharp turn and the derivatives from the left and right did not match. The second graph had a “cusp” where secant line slope approach positive infinity from one side and negative infinity from the other. The third graph had a “vertical tangent line” where the secant line slopes approach positive or negative infinity from both sides.
    [Show full text]
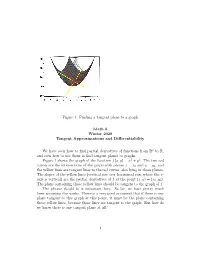
  • Figure 1: Finding a Tangent Plane to a Graph
    Figure 1: Finding a tangent plane to a graph Math 8 Winter 2020 Tangent Approximations and Differentiability We have seen how to find partial derivatives of functions from R2 to R, and seen how to use them to find tangent planes to graphs. Figure 1 shows the graph of the function f(x; y) = x2 + y2. The two red curves are the intersections of the graph with planes x = x0 and y = y0, and the yellow lines are tangent lines to the red curves, also lying in those planes. The slopes of the yellow lines (vertical rise over horizontal run, where the z- axis is vertical) are the partial derivatives of f at the point (x; y) = (x0; y0). The plane containing those yellow lines should be tangent to the graph of f. The phrase should be is important here. So far, we have pretty much been assuming this works. There is a very good argument that if there is any plane tangent to this graph at this point, it must be the plane containing these yellow lines, because those lines are tangent to the graph. But how do we know there is any tangent plane at all? 1 2xy Figure 2: Graph of f(x; y) = . px2 + y2 If (x; y) = (r sin θ; r cos θ), then f(x; y) = r sin(2θ). It turns out that a function can have partial derivatives without its graph having a tangent plane. Here is an example. Figure 2 shows two different pictures of a portion of the graph of the function 2xy f(x; y) = : px2 + y2 The x- and y-axes are drawn in red, and the intersection of the graph with the vertical plane y = x is drawn in yellow.
    [Show full text]
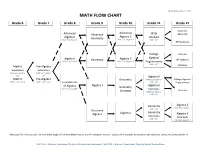
  • Math Flow Chart
    Updated November 12, 2014 MATH FLOW CHART Grade 6 Grade 7 Grade 8 Grade 9 Grade 10 Grade 11 Grade 12 Calculus Advanced Advanced Advanced Math AB or BC Algebra II Algebra I Geometry Analysis MAP GLA-Grade 8 MAP EOC-Algebra I MAP - ACT AP Statistics College Calculus Algebra/ Algebra I Geometry Algebra II AP Statistics MAP GLA-Grade 8 MAP EOC-Algebra I Trigonometry MAP - ACT Math 6 Pre-Algebra Statistics Extension Extension MAP GLA-Grade 6 MAP GLA-Grade 7 or or Algebra II Math 6 Pre-Algebra Geometry MAP EOC-Algebra I College Algebra/ MAP GLA-Grade 6 MAP GLA-Grade 7 MAP - ACT Foundations Trigonometry of Algebra Algebra I Algebra II Geometry MAP GLA-Grade 8 Concepts Statistics Concepts MAP EOC-Algebra I MAP - ACT Geometry Algebra II MAP EOC-Algebra I MAP - ACT Discovery Geometry Algebra Algebra I Algebra II Concepts Concepts MAP - ACT MAP EOC-Algebra I Additional Full Year Courses: General Math, Applied Technical Mathematics, and AP Computer Science. Calculus III is available for students who complete Calculus BC before grade 12. MAP GLA – Missouri Assessment Program Grade Level Assessment; MAP EOC – Missouri Assessment Program End-of-Course Exam Mathematics Objectives Calculus Mathematical Practices 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning. Linear and Nonlinear Functions • Write equations of linear and nonlinear functions in various formats.
    [Show full text]
  • Is Differentiable at X=A Means F '(A) Exists. If the Derivative
    The Derivative as a Function Differentiable: A function, f(x), is differentiable at x=a means f '(a) exists. If the derivative exists on an interval, that is , if f is differentiable at every point in the interval, then the derivative is a function on that interval. f ( x h ) f ( x ) Definition: f ' ( x ) lim . h 0 h ( x h ) 2 x 2 x 2 2 xh h 2 x 2 Example: f ( x ) x 2 f ' ( x ) lim lim lim (2 x h ) 2 x h 0 h h 0 h h 0 Exercise: Show the derivative of a line is the slope of the line. That is, show (mx + b)' = m The derivative of a constant is 0. Linear Rule: If A and B are numbers and if f '(x) and g '(x) both exist then the derivative of Af+Bg at x is Af '(x) + Bg '(x). That is (Af + Bg)'(x)= Af '(x) + Bg '(x) Applying the linear rule for derivatives, we can differentiate any quadratic. Example: g ( x ) 4 x 2 6 x 7 g ' ( x ) 4(2 x ) 6 8 x 6 We can find the tangent line to g at a given point. Example: For g(x) as above, find the equation of the tangent line at (2, g(2)). g(2)=4(4)-12+7= 11 so the point of tangency is (2, 11). To get the slope, we plug x=2 into g '(x)=8x-6 the slope is g'(2)= 8(2)-6=10 so the tangent line is y = 10(x - 2) + 11 Notations for the derivative: df df f ' ( x ) f ' (a ) dx dx x a If a function is differentiable at x=a then it must be continuous at a.
    [Show full text]
  • Advanced Placement Calculus Advanced Placement Physics
    AP Calc/Phys ADVANCED PLACEMENT CALCULUS ADVANCED PLACEMENT PHYSICS DESCRIPTION In this integrated course students will be enrolled in both AP Calculus and AP Physics. Throughout the year, topics will be covered in one subject that will supplement, reinforce, enhance, introduce, build on and extend topics in the other. Some tests will be combined, as will the exams, and some of the classes will be team taught. Calculus instruction is typically demanding and covers the topics included in the nationally approved Advanced Placement curriculum. Topics include the slope of a curve, derivatives of algebraic and transcendental functions, properties of limits, the rate of change of a function, optimization problems, Rolles and Mean Value Theorems, integration, the trapezoidal and Simpson's Rules, parametric equations and the use of scientific calculators. Physics instruction provides a systematic treatment of all of the topics required and recommended in the national AP curriculum as preparation for the AP "C" exam, specifically the mechanics part. The course is calculus based, and emphasizes not only the development of problem solving skills but also critical thinking skills. The course focuses on mechanics (statics, dynamics, momentum energy, etc.); electricity and magnetism; thermodynamics; wave phenomena (primarily electromagnetic waves); geometric optics; and, if time permits, relativity, modern and nuclear physics. I. Functions, Graphs and Limits A. Analysis of graphs. B. Limits of functions, including one-sided limits 1. Calculating limits using algebra. 2. Estimating limits from graphs or tables of data. C. Asymptotic and unbounded behavior. 1. Understanding asymptotes in terms of graphical behavior. 2. Describing asymptotic behavior in terms of limits involving infinity.
    [Show full text]