DOCSLIB.ORG

Applications of Differentiation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Applications of Differentiation Not for Sale Applications of 2 Differentiation What You’ll Learn Why It’s Important 2.1 Using First Derivatives to Classify Maximum In this chapter, we explore many applications and Minimum Values and Sketch Graphs of differentiation. We learn to find maximum 2.2 Using Second Derivatives to Classify and minimum values of functions, and that skill Maximum and Minimum Values and Sketch allows us to solve many kinds of problems in Graphs which we need to find the largest and/or smallest 2.3 Graph Sketching: Asymptotes and Rational value in a real-world situation. Our differentiation Functions skills will be applied to graphing, and we will use 2.4 Using Derivatives to Find Absolute differentials to approximate function values. We Maximum and Minimum Values will also use differentiation to explore elasticity of 2.5 Maximum–Minimum Problems; Business, demand and related rates. Economics, and General Applications 2.6 Marginals and Differentials 2.7 Elasticity of Demand 2.8 Implicit Differentiation and Related Rates Where It’s Used y C(r) Minimizing Cost: Minimizing cost is a common goal in 0.32 manufacturing. For example, cylindrical food cans come in a 3 (4.21, 0.2673) variety of sizes. Suppose a soup can is to have a volume of 250 cm . 0.24 2 The cost of material for the two circular ends is $0.0008 cm , and 0.16 the cost of material for the side is $0.0015 cm2. What dimensions > Cost (in dollars) 0.08 minimize the cost of material for the soup can?(This problem > appears as Example 3 in Section 2.5.) 20 4 6 8 r Radius (in centimeters) 188 Copyright 2016 Pearson. All rights reserved. M02_BITT9391_11_SE_C02.1.indd 188 29/10/14 4:39 PM Not for Sale 2.1 ● Using First Derivatives to Classify Maximum and Minimum Values and Sketch Graphs 189 Using First Derivatives to Classify Maximum and Minimum Values 2.1 and Sketch Graphs The graph below shows a typical life cycle of a retail product and is similar to graphs ● Find relative extrema of a continuous function using the we will consider in this chapter. Note that the number of items sold varies with re- First-Derivative Test. spect to time. Sales begin at a small level and increase to a point of maximum sales, after which they taper off to a low level, possibly because of new competitive prod- ● Sketch graphs of continuous ucts. The company then rejuvenates the product by making improvements. Think functions. about versions of certain products: televisions can be traditional, flat-screen, or high- definition; music recordings have been produced as phonograph (vinyl) records, au- diotapes, compact discs, and MP3 files. Where might each of these products be in a typical product life cycle? Is the curve below appropriate for each product? S PRODUCT LIFE CYCLE Sales of product t Introduction Growth Maturity Decline Rejuvenation Time Finding the largest and smallest values of a function—that is, the maximum and minimum values—has extensive applications. The first and second derivatives of a function can provide information for graphing functions and finding maximum and minimum values. Increasing and Decreasing Functions If the graph of a function rises from left to right over an interval I, the function is said to be increasing on, or over, I. If the graph drops from left to right, the function is said to be decreasing on, or over, I. y y f Decreasing f(b) g(a) f(a) g(b) Increasing g a b x a b x If the input a is less than the input b, If the input a is less than the input b, then the output for a is less than the then the output for a is greater than the output for b. output for b. Copyright 2016 Pearson. All rights reserved. M02_BITT9391_11_SE_C02.1.indd 189 29/10/14 4:39 PM Not for Sale 190 CHAPTER 2 ● Applications of Differentiation TECHNOLOGY CONNECTION We can define these concepts as follows. Exploratory DEFINITIONS Graph the function A function f is increasing over I if, for every a and b in I, 1 3 2 f x = - 3x + 6x - 11x - 50 if a 6 b, then f a 6 f b . and1 2 its derivative A function f is decreasing over I if, for every a and b in I, 2 1 2 1 2 f′ x = -x + 12x - 11 if a 6 b, then f a 7 f b . using1 2 the window -10, 25, -100, 150 , with Xscl = 5 and 1 2 1 2 3 Yscl = 25. Then TRACE from left The above definitions can be restated in terms of secant lines as shown below. to right along4 each graph. Mov- ing the cursor from left to right, f b - f a f b - f a Increasing: 7 0. Decreasing: 6 0. note that the x-coordinate always b a b a increases. If the function is 1 2 - 1 2 1 2 - 1 2 increasing, the y-coordinate will y y increase as well. If a function is decreasing, the y-coordinate will f f(b) f(a) decrease. Slope of secant Slope of secant Over what intervals is f line is positive. line is negative. increasing? Over what intervals is f f(a) decreasing? Over what intervals is f′ f positive? Over what intervals is f′ f(b) negative? What rules might relate the sign of f′ to the behavior of f? a b x a b x The following theorem shows how we can use the derivative (the slope of a tan- gent line) to determine whether a function is increasing or decreasing. THEOREM 1 Let f be differentiable over an open interval I. If f′ x 7 0 for all x in I, then f is increasing over I. If f′ x 6 0 for all x in I, then f is decreasing over I. 1 2 1 2 1 3 2 Theorem 1 is illustrated in the following graph of f x = 3x - x + 3. 1 2 4± ±1, 3 y 1 f(x)= ± x3 ±x + 2± 3 3 1 ±2 ±1 (1, 0) x Increasing Decreasing Increasing f9(x) > 0 f9(x) < 0 f9(x) > 0 f is increasing over the intervals (±, ∞ ±1) and (1, ∞); slopes of tangent lines are positive. f is decreasing over the interval (±1, 1); slopes of tangent lines are negative. Note in the graph above that x = -1 and x = 1 are not included in any interval over which the function is increasing or decreasing. These values are examples of critical values. Copyright 2016 Pearson. All rights reserved. M02_BITT9391_11_SE_C02.1.indd 190 29/10/14 4:39 PM Not for Sale 2.1 ● Using First Derivatives to Classify Maximum and Minimum Values and Sketch Graphs 191 Critical Values Consider the following graph of a continuous function f. y f x c1 c2 c3 c4 c5 c6 c7 c8 Note the following: 1. f′ x = 0 at x = c1, c2, c4, c7, and c8. That is, the tangent line to the graph is horizontal for these values. 1 2 2. f′ x does not exist at x = c3, c5, and c6. The tangent line is vertical at c3, and there are corners at both c5 and c6. (See also the discussion at the end of Section1 2 1.4.) DEFINITION A critical value of a function f is any number c in the domain of f for which the tangent line at c, f c is horizontal or for which the derivative does not exist. That is, c is a critical value if f c exists and 1 1 22 f′ c = 0 or f′ c does1 2 not exist. 1 2 1 2 Thus, in the graph of f above: ● c1, c2, c4, c7, and c8 are critical values because f′ c = 0 for each value. ● c , c , and c are critical values because f′ c does not exist for each value. 3 5 6 1 2 A continuous function can change from increasing1 2 to decreasing or from decreas- ing to increasing only at a critical value. In the above graph, c1, c2, c4, c5, c6, and c7 separate intervals over which the function f increases from those in which it decreases or intervals in which the function decreases from those in which it in- creases. Although c3 and c8 are critical values, they do not separate intervals over which the function changes from increasing to decreasing or from decreasing to increasing. Copyright 2016 Pearson. All rights reserved. M02_BITT9391_11_SE_C02.1.indd 191 29/10/14 4:39 PM Not for Sale 192 CHAPTER 2 ● Applications of Differentiation Finding Relative Maximum and Minimum Values Now consider a graph with “peaks” and “valleys” at x = c1, c2, and c3. y f(b) Relative Maxima maximum f f(c2) f(c3) Relative Minima f(a) minimum f(c1) abc1 c2 c3 x Here, f c2 is an example of a relative maximum (plural: maxima). Each of f c1 and f c3 is called a relative minimum (plural: minima). Collectively, maximum and minimum1 2values are called extrema (singular: extremum). 1 2 1 2 DEFINITIONS Let I be the domain of f. f c is a relative minimum if there exists within I an open interval I1 containing c such that f c … f x , for all x in I1; 1 2 and 1 2 1 2 f c is a relative maximum if there exists within I an open interval I2 containing c such that f c Ú f x , for all x in I2.
Load more

Recommended publications
  • CALCULUS I §2.2: Differentiability, Graphs, and Higher Derivatives
    MATH 12002 - CALCULUS I x2.2: Differentiability, Graphs, and Higher Derivatives Professor Donald L. White Department of Mathematical Sciences Kent State University D.L. White (Kent State University) 1 / 10 Differentiability The process of finding a derivative is called differentiation, and we define: Definition Let y = f (x) be a function and let a be a number. We say f is differentiable at x = a if f 0(a) exists. What does this mean in terms of the graph of f ? If f 0(a) = lim f (a+h)−f (a) exists, then f (a) must be defined. h!0 h Since the denominator is approaching 0, in order for the limit to exist, the numerator must also approach 0; that is, lim (f (a + h) − f (a)) = 0: h!0 Hence lim f (a + h) = f (a), and so lim f (x) = f (a), h!0 x!a meaning f must be continuous at x = a. D.L. White (Kent State University) 2 / 10 Differentiability But being continuous at a is not enough to make f differentiable at a. Differentiability is \continuity plus." The \plus" is smoothness: the graph cannot have a sharp \corner" at a. The graph also cannot have a vertical tangent line at x = a: the slope of a vertical line is not a real number. Hence, in order for f to be differentiable at a, the graph of f must 1 be continuous at a, 2 be smooth at a, i.e., no sharp corners, and 3 not have a vertical tangent line at x = a.
    [Show full text]
  • Example: Using the Grid Provided, Graph the Function
    3.2 Differentiability Calculus 3.2 DIFFERENTIABILITY Notecards from Section 3.2: Where does a derivative NOT exist, Definition of a derivative (3rd way). The focus on this section is to determine when a function fails to have a derivative. For all you non-English majors, the word differentiable means you are able to take a derivative, or the derivative exists. Example 1: Using the grid provided, graph the function fx( ) = x − 3 . y a) What is fx'( ) as x → 3− ? b) What is fx'( ) as x → 3+ ? c) Is f continuous at x = 3? d) Is f differentiable at x = 3? x 2 Example 2: Graph fx x3 y a) Describe the derivative of f (x) as x approaches 0 from the left and the right. 2 b) Suppose you found fx' . 33 x x What is the value of the derivative when x = 0? 3 Example 3: Graph fx x y a) Describe the derivative of f (x) as x approaches 0 from the left and the right. 1 b) Suppose you found fx' . 33 x2 What is the value of the derivative when x = 0? x These last three examples (along with any graph that is not continuous) are NOT differentiable. The first graph had a “corner” or a sharp turn and the derivatives from the left and right did not match. The second graph had a “cusp” where secant line slope approach positive infinity from one side and negative infinity from the other. The third graph had a “vertical tangent line” where the secant line slopes approach positive or negative infinity from both sides.
    [Show full text]
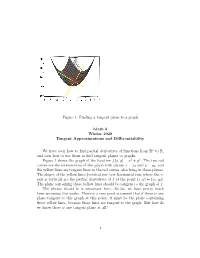
  • Figure 1: Finding a Tangent Plane to a Graph
    Figure 1: Finding a tangent plane to a graph Math 8 Winter 2020 Tangent Approximations and Differentiability We have seen how to find partial derivatives of functions from R2 to R, and seen how to use them to find tangent planes to graphs. Figure 1 shows the graph of the function f(x; y) = x2 + y2. The two red curves are the intersections of the graph with planes x = x0 and y = y0, and the yellow lines are tangent lines to the red curves, also lying in those planes. The slopes of the yellow lines (vertical rise over horizontal run, where the z- axis is vertical) are the partial derivatives of f at the point (x; y) = (x0; y0). The plane containing those yellow lines should be tangent to the graph of f. The phrase should be is important here. So far, we have pretty much been assuming this works. There is a very good argument that if there is any plane tangent to this graph at this point, it must be the plane containing these yellow lines, because those lines are tangent to the graph. But how do we know there is any tangent plane at all? 1 2xy Figure 2: Graph of f(x; y) = . px2 + y2 If (x; y) = (r sin θ; r cos θ), then f(x; y) = r sin(2θ). It turns out that a function can have partial derivatives without its graph having a tangent plane. Here is an example. Figure 2 shows two different pictures of a portion of the graph of the function 2xy f(x; y) = : px2 + y2 The x- and y-axes are drawn in red, and the intersection of the graph with the vertical plane y = x is drawn in yellow.
    [Show full text]
  • Is Differentiable at X=A Means F '(A) Exists. If the Derivative
    The Derivative as a Function Differentiable: A function, f(x), is differentiable at x=a means f '(a) exists. If the derivative exists on an interval, that is , if f is differentiable at every point in the interval, then the derivative is a function on that interval. f ( x h ) f ( x ) Definition: f ' ( x ) lim . h 0 h ( x h ) 2 x 2 x 2 2 xh h 2 x 2 Example: f ( x ) x 2 f ' ( x ) lim lim lim (2 x h ) 2 x h 0 h h 0 h h 0 Exercise: Show the derivative of a line is the slope of the line. That is, show (mx + b)' = m The derivative of a constant is 0. Linear Rule: If A and B are numbers and if f '(x) and g '(x) both exist then the derivative of Af+Bg at x is Af '(x) + Bg '(x). That is (Af + Bg)'(x)= Af '(x) + Bg '(x) Applying the linear rule for derivatives, we can differentiate any quadratic. Example: g ( x ) 4 x 2 6 x 7 g ' ( x ) 4(2 x ) 6 8 x 6 We can find the tangent line to g at a given point. Example: For g(x) as above, find the equation of the tangent line at (2, g(2)). g(2)=4(4)-12+7= 11 so the point of tangency is (2, 11). To get the slope, we plug x=2 into g '(x)=8x-6 the slope is g'(2)= 8(2)-6=10 so the tangent line is y = 10(x - 2) + 11 Notations for the derivative: df df f ' ( x ) f ' (a ) dx dx x a If a function is differentiable at x=a then it must be continuous at a.
    [Show full text]
  • Unit #5 - Implicit Differentiation, Related Rates
    Unit #5 - Implicit Differentiation, Related Rates Some problems and solutions selected or adapted from Hughes-Hallett Calculus. Implicit Differentiation 1. Consider the graph implied by the equation (c) Setting the y value in both equations equal to xy2 = 1. each other and solving to find the intersection point, the only solution is x = 0 and y = 0, so What is the equation of the line through ( 1 ; 2) 4 the two normal lines will intersect at the origin, which is also tangent to the graph? (x; y) = (0; 0). Differentiating both sides with respect to x, Solving process: dy 3 3 y2 + x 2y = 0 (x − 4) + 3 = − (x − 4) − 3 dx 4 4 3 3 so x − 3 + 3 = − x + 3 − 3 4 4 dy −y2 3 3 = x = − x dx 2xy 4 4 6 x = 0 4 dy At the point ( 1 ; 2), = −4, so we can use the x = 0 4 dx point/slope formula to obtain the tangent line y = −4(x − 1=4) + 2 Subbing back into either equation to find y, e.g. y = 3 (0 − 4) + 3 = −3 + 3 = 0. 2. Consider the circle defined by x2 + y2 = 25 4 3. Calculate the derivative of y with respect to x, (a) Find the equations of the tangent lines to given that the circle where x = 4. (b) Find the equations of the normal lines to x4y + 4xy4 = x + y this circle at the same points. (The normal line is perpendicular to the tangent line.) Let x4y + 4xy4 = x + y. Then (c) At what point do the two normal lines in- dy dy dy 4x3y + x4 + (4x) 4y3 + 4y4 = 1 + tersect? dx dx dx hence Differentiating both sides, dy 4yx3 + 4y4 − 1 = : dx 1 − x4 − 16xy3 d d x2 + y2 = (25) dx dx 4.
    [Show full text]
  • Limit Definition of the Derivative
    Limit Definition of the Derivative We define the derivative of a function f(x) at x = x0 as 0 f(x0 + h) − f(x0) 0 f(z) − f(x0) f (x0) = lim or f (x0) = lim h!0 h z!x0 z − x0 if these limits exist! We'll usually find the derivative as a function of x and then plug in x = a. (This allows us to quickly find the value of the derivative a multiple values of a without having to evaluate a limit for each of them.) f(x + h) − f(x) f(z) − f(x) f 0(x) = lim or f 0(x) = lim h!0 h z!x z − x (The book also defines left- and right-hand derivatives in a manner analogous to left- and right-hand limits or continuity.) Notation and Higher Order Derivatives The following are all different ways of writing the derivative of a function y = f(x): d df dy · f 0(x); y0; [f(x)] ; ; ;D [f(x)] ;D [f(x)] ; f dx dx dx x (The brackets in the third, sixth, and seventh forms may be changed to parentheses or omitted entirely.) If we take the derivative of the derivative we get the second derivative. We can also find other higher order derivatives (third, fourth, fifth, etc.). The notation for these is as follows: Order Notation d2 d2f d2y ·· Second f 00(x); y00; f(x); ; ;D2f(x);D2f(x); f dx2 dx2 dx2 x 3 3 3 d d f d y ) Third f 000(x); y000; f(x); ; ;D3f(x);D3f(x); f dx3 dx3 dx3 x d4 d4f d4y Fourth f (4)(x); y(4); f(x); ; ;D4f(x);D4f(x) dx4 dx4 dx4 x dn dnf dny nth f (n)(x); y(n); f(x); ; ;Dnf(x);Dnf(x) dxn dxn dxn x When is a Function Not Differentiable? There is a theorem relating differentiability and continuity which says that if a function is differentiable at a point then it is also continuous there.
    [Show full text]
  • Differential Calculus – Definitions, Rules and Theorems Sarah Brewer, Alabama School of Math and Science
    Differential Calculus – Definitions, Rules and Theorems Sarah Brewer, Alabama School of Math and Science Precalculus Review Functions, Domain and Range : a function from to assigns to each a unique the domain of is the set - the set of all real numbers for which the function is defined 푓 푋 → 푌 푓 푋 푌 푥 ∈ 푋 푦 ∈ 푌 is the image of under , denoted ( ) 푓 푋 the range of is the subset of consisting of all images of numbers in 푌 푥 푓 푓 푥 is the independent variable, is the dependent variable 푓 푌 푋 is one-to-one if to each -value in the range there corresponds exactly one -value in the domain 푥 푦 is onto if its range consists of all of 푓 푦 푥 푓Implicit v. Explicit Form 푌 3 + 4 = 8 implicitly defines in terms of = + 2 explicit form 푥 푦 푦 푥 3 푦Graphs− 4 o푥f Functions A function must pass the vertical line test A one-to-one function must also pass the horizontal line test Given the graph of a basic function = ( ), the graph of the transformed function, = ( + ) + = + + 푦 푓 푥, can be found using the following rules: 푐 - vertical stretch (mult. -values by ) 푦 푎푓 푏푥 푐 푑 푎푓 �푏 �푥 푏�� 푑 - horizontal stretch (divide -values by ) 푎 푦 푎 – horizontal shift (shift left if > 0, right if < 0) 푏푐 푥 푐 푏 푐 > 0 < 0 푏 - vertical shift (shift up if 푏 , down if 푏 ) You푑 should know the basic 푑graphs of: 푑 = , = , = , = | |, = , = , = , 3 1 = sin , =2 cos , 3 = tan , = csc , = sec , = cot 푦 푥 푦 푥 푦 푥 푦 푥 푦 √푥 푦 √푥 푦 푥 For푦 further푥 discussion푦 푥 of 푦graphing,푥 see푦 Precal 푥and푦 Trig Guides푥 푦 to Graphing푥 Elementary Functions Algebraic functions (polynomial, radical, rational) - functions that can be expressed as a finite number of sums, differences, multiples, quotients, & radicals involving Functions that are not algebraic are trancendental (eg.
    [Show full text]
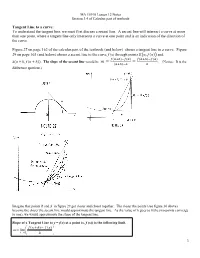
  • Tangent Line to a Curve: to Understand the Tangent Line, We Must First Discuss a Secant Line
    MA 15910 Lesson 12 Notes Section 3.4 of Calculus part of textbook Tangent Line to a curve: To understand the tangent line, we must first discuss a secant line. A secant line will intersect a curve at more than one point, where a tangent line only intersects a curve at one point and is an indication of the direction of the curve. Figure 27 on page 162 of the calculus part of the textbook (and below) shows a tangent line to a curve. Figure 29 on page 163 (and below) shows a secant line to the curve f (x) through points 푅(푎, 푓(푎)) and 푓(푎+ℎ)−푓(푎) 푓(푎+ℎ)−푓(푎) 푆(푎 + ℎ, 푓(푎 + ℎ)). The slope of the secant line would be 푚 = = . (Notice: It is the (푎+ℎ)−푎 ℎ difference quotient.) Imagine that points R and S in figure 29 get closer and closer together. The closer the points (see figure 30 above) become the closer the secant line would approximate the tangent line. As the value of h goes to 0(the two points converge to one), we would approximate the slope of the tangent line. Slope of a Tangent Line to y = f(x) at a point (x, f (x)) is the following limit. f()() x h f x m lim h0 h 1 Examples: Ex 1: Find the equation of the secant line through the curve y f( x ) x2 x containing point (1,1) and (3,6) . 6 1 5 m 3 1 2 Notice: These 5 are the same yx1 ( 1) 2 function.
    [Show full text]
  • 2.1: the Derivative and the Tangent Line Problem
    2.1.1 2.1: The Derivative and the Tangent Line Problem What is the definition of a “tangent line to a curve”? To answer the difficulty in writing a clear definition of a tangent line, we can define it as the limiting position of the secant line as the second point approaches the first. Definition: The tangent line to the curve yfx () at the point (,afa ()) is the line through P with slope f ()xfa () m lim provided this limit exists. xa xa Equivalently, f ()()ah fa m lim provided this limit exists. h0 h Note: If the tangent line is vertical, this limit does not exist. In the case of a vertical tangent, the equation of the tangent line is x a . Note: The slope of the tangent line to the graph of f at the point (,afa ()) is also called the slope of the graph of f at x a . How to get the second expression for slope: Instead of using the points (,afa ()) and (,x fx ()) on the secant line and letting x a , we can use (,afa ()) and (,())ahfah and let h 0 . 2.1.2 Example 1: Find the slope of the curve yx 412 at the point (3,37) . Find the equation of the tangent line at this point. Example 2: Find an equation of the tangent line to the curve y x3 at the point (1,1) . Example 3: Determine the equation of the tangent line to f ()xx at the point where x 2 . 2.1.3 The derivative: The derivative of a function at x is the slope of the tangent line at the point (x ,fx ( )) .
    [Show full text]
  • 2.1 the Derivative and the Tangent Line Problem
    96 Chapter 2 Differentiation 2.1 The Derivative and the Tangent Line Problem Find the slope of the tangent line to a curve at a point. Use the limit definition to find the derivative of a function. Understand the relationship between differentiability and continuity. The Tangent Line Problem Calculus grew out of four major problems that European mathematicians were working on during the seventeenth century. 1. The tangent line problem (Section 1.1 and this section) 2. The velocity and acceleration problem (Sections 2.2 and 2.3) 3. The minimum and maximum problem (Section 3.1) 4. The area problem (Sections 1.1 and 4.2) Each problem involves the notion of a limit, and calculus can be introduced with any of the four problems. A brief introduction to the tangent line problem is given in Section 1.1. Although partial solutions to this problem were given by Pierre de Fermat (1601–1665), René Descartes (1596–1650), Christian Huygens (1629–1695), and Isaac Barrow (1630–1677), credit for the first general solution is usually given to Isaac Newton (1642–1727) and Gottfried Leibniz (1646–1716). Newton’s work on this problem ISAAC NEWTON (1642–1727) stemmed from his interest in optics and light refraction. In addition to his work in calculus, What does it mean to say that a line is Newton made revolutionary y contributions to physics, including tangent to a curve at a point? For a circle, the the Law of Universal Gravitation tangent line at a point P is the line that is and his three laws of motion.
    [Show full text]
  • Basic Calculus Refresher
    1 BASIC CALCULUS REFRESHER Ismor Fischer, Ph.D. Dept. of Statistics UW-Madison 1. Introduction. This is a very condensed and simplified version of basic calculus, which is a prerequisite for many courses in Mathematics, Statistics, Engineering, Pharmacy, etc. It is not comprehensive, and absolutely not intended to be a substitute for a one-year freshman course in differential and integral calculus. You are strongly encouraged to do the included Exercises to reinforce the ideas. Important mathematical terms are in boldface; key formulas and concepts are boxed and highlighted (). To view a color .pdf version of this document (recommended), see http://www.stat.wisc.edu/~ifischer. 2. Exponents – Basic Definitions and Properties For any real number base x, we define powers of x: x0 = 1, x1 = x, x2 = x x, x3 = x x x, etc. (The exception is 00, which is considered indeterminate.) Powers are also called exponents. Examples: 50 = 1, ( 11.2)1 = 11.2, (8.6)2 = 8.6 8.6 = 73.96, 103 = 10 10 10 = 1000, ( 3)4 = ( 3) ( 3) ( 3) ( 3) = 81. Also, we can define fractional exponents in terms of roots, such as x1/2 = x , the square root of x. 1/3 3 2/3 3 2 m/n n m Similarly, x = x , the cube root of x, x = ( x) , etc. In general, we have x = ( x) , i.e., the nth root of x, raised to the mth power. 3 3 3 Examples: 641/2 = 64 = 8, 643/2 = ( 64) = 83 = 512, 641/3 = 64 = 4, 642/3 = ( 64) = 42 = 16. r 1 1 1 2 1 1/2 1 1 Finally, we can define negative exponents: x = r .
    [Show full text]
  • MORE on VERTICAL TANGENT LINES 1. Introduction in Thomas
    MORE ON VERTICAL TANGENT LINES MATTHEW BOND 1. Introduction In Thomas' Calculus, 12th Edition, section 3.1, problems 35-46, we studied func- tions having a vertical tangent at a point. Definition: A function f has a vertical tangent at a point x0 if one of the two following things occur: f(x + h) − f(x ) f(x + h) − f(x ) lim 0 0 = 1 or lim 0 0 = −∞ (1.1) h!0 h h!0 h (Reminder: The 2-sided limit must be one of these two values. If the one-sided limits are the two different values 1 and −∞, then this is called a cusp of f.) Once you have thoroughly covered section 4.2 of Thomas' Calculus, 12th ed. (the Mean Value Theorem) or something equivalent to that, you are ready to apply the Mean Value Theorem to investigate further properties of vertical tangent lines. Question: Suppose that a function f is differentiable on (a; x0) and also differ- entiable on (x0; b), and also continuous at the point x0. Then is it true that f has a vertical tangent at x0 if and only if one of the following two things occurs? lim f 0(x) = 1 or lim f 0(x) = −∞ (1.2) x!x0 x!x0 The answer is no. (1.2) implies (1.1), but NOT vice versa. That is, if f is continuous at x0, then (1.2) always results in a vertical tangent, but sometimes a vertical tangent can still exist even if (1.2) does not occur. In the next two sections, we will investigate both of these facts.
    [Show full text]