DOCSLIB.ORG

Dynamics in Several Complex Variables: Endomorphisms of Projective Spaces and Polynomial-Like Mappings

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Dynamics in Several Complex Variables: Endomorphisms of Projective Spaces and Polynomial-Like Mappings Dynamics in Several Complex Variables: Endomorphisms of Projective Spaces and Polynomial-like Mappings Tien-Cuong Dinh and Nessim Sibony Abstract The emphasis of this introductory course is on pluripotential methods in complex dynamics in higher dimension. They are based on the compactness prop- erties of plurisubharmonic (p.s.h.) functions and on the theory of positive closed currents. Applications of these methods are not limited to the dynamical systems that we consider here. Nervertheless, we choose to show their effectiveness and to describe the theory for two large familiesofmaps:theendomorphismsofprojective spaces and the polynomial-like mappings. The first section deals with holomorphic endomorphisms of the projective space Pk.Weestablishthefirstpropertiesandgive several constructions for the Green currents T p and the equilibrium measure µ = T k. The emphasis is on quantitative properties and speed of convergence. We then treat equidistribution problems. We show the existence of a proper algebraic set E ,totally 1 invariant, i.e. f − (E )=f (E )=E ,suchthatwhena E ,theprobabilitymeasures, n "∈ equidistributed on the fibers f − (a),convergetowardstheequilibriummeasureµ, as n goes to infinity. A similar result holds for the restriction of f to invariant sub- varieties. We survey the equidistribution problem when points are replaced with varieties of arbitrary dimension, and discuss the equidistribution of periodic points. We then establish ergodic properties of µ:K-mixing,exponentialdecayofcorrela- tions for various classes of observables, central limit theorem and large deviations theorem. We heavily use the compactness of the space DSH(Pk) of differences of quasi-p.s.h. functions. In particular, we show that the measure µ is moderate, i.e. α ϕ k µ,e | | c,onboundedsetsofϕ in DSH(P ),forsuitablepositiveconstants $ %≤ α,c.Finally,westudytheentropy,theLyapounovexponentsandthedimension of µ.Thesecondsectiondevelopsthetheoryofpolynomial-likemaps,i.e.proper T.-C. Dinh UPMC Univ Paris 06, UMR7586,Institut de Math´ematiques de Jussieu, F-75005 Paris, France e-mail: [email protected] N. Sibony Universit´eParis-Sud11,Math´ematique - Bˆatiment 425, 91405 Orsay, France e-mail: [email protected] G. Gentili et al. (eds.), Holomorphic Dynamical Systems,165 Lecture Notes in Mathematics 1998, DOI 10.1007/978-3-642-13171-4 4, c Springer-Verlag Berlin Heidelberg 2010 ! 166 Tien-Cuong Dinh and Nessim Sibony k holomorphic maps f : U V where U,V are open subsets of C with V convex → and U ! V .Weintroducethedynamicaldegreesforsuchmapsandconstructthe equilibrium measure µ of maximal entropy. Then, under a natural assumption on the dynamical degrees, we prove equidistribution properties of points and various statistical properties of the measure µ.Theassumptionisstableundersmallpertu- bations on the map. We also study the dimension of µ,theLyapounovexponents and their variation. Our aim is to get a self-contained text that requires only a min- imal background. In order to help the reader, an appendix gives the basics on p.s.h. functions, positive closed currents and super-potentials on projective spaces. Some exercises are proposed and an extensive bibliography is given. Introduction These notes are based on a series of lectures given by the authors at IHP in 2003, Luminy in 2007, Cetraro in 2008 and Bedlewo 2008. The purpose is to provide an introduction to some developments in dynamics of several complex variables. We have chosen to treat here only two sections of the theory: the dynamics of endomor- phisms of the projective space Pk and the dynamics of polynomial-like mappings in higher dimension. Besides the basic notions and results, we describe the recent developments and the new tools introduced in the theory. These tools are useful in other settings. We tried to give a complete picture of the theory for the above families of dynamical systems. Meromorphic maps on compact K¨ahler manifolds, in particular polynomial automorphisms of Ck,willbestudiedinaforthcoming survey. Let us comment on how complex dynamics fits in the general theory of dynamical systems. The abstract ergodic theory is well-developed with remark- able achievements like the Oseledec-Pesin theory. It is however difficult to show in concrete examples that an invariant measure satisfies exponential decay of corre- lations for smooth observables or is hyperbolic, i.e. has only non-zero Lyapounov exponents, see e.g. Benedicks-Carleson [BC], Viana [V], L.S. Young [Y, Y1]. One of our goals is to show that holomorphic dynamics in several variables provides remarkable examples of non-uniformly hyperbolic systems where the abstract the- ory can be applied. Powerful tools from the theory of several complex variables permit to avoid delicate combinatorial estimates. Complex dynamics also require a development of new tools like the calculus on currents and the introduction of new spaces of observables, which are of independent interest. 1 Complex dynamics in dimension one, i.e. dynamics of rational maps on P , is well-developed and has in some sense reached maturity. The main tools there are Montel’s theorem on normal families, the Riemann measurable mapping theo- rem and the theory of quasi-conformal maps, see e.g. Beardon, Carleson-Gamelin [BE, CG]. When dealing with maps in several variables such tools are not available: the Kobayashi hyperbolicity of a manifold and the possibility to apply normal fam- ily arguments, are more difficult to check. Holomorphic maps in several variables are not conformal and there is no Riemann measurable mapping theorem. Dynamics in Several Complex variables 167 The theory in higher dimension is developed using mostly pluripotential theory, i.e. the theory of plurisubharmonic (p.s.h. for short) functions and positive closed currents. The Montel’s compactness property is replaced with the compactness properties of p.s.h. or quasi-p.s.h. functions. Another crucial tool is the use of good estimates for the ddc-equation in various settings. One of the main ideas is: in order to study the statistical behavior of orbits of a holomorphic map, we consider its ac- tion on some appropriate functional spaces. We then decompose the action into the “harmonic” part and the “non-harmonic” one. This is done solving a ddc-equation with estimates. The non-harmonic part of the dynamical action may be controled thanks to good estimates for the solutions of a ddc-equation. The harmonic part can be treated using either Harnack’s inequality in the local setting or the linear action of maps on cohomology groups in the case of dynamics on compact K¨ahler manifolds. This approach has permitted to give a satisfactory theory of the ergodic properties of holomorphic and meromorphic dynamical systems: construction of the measure of maximal entropy, decay of correlations, central limit theorem, large deviations theorem, etc. with respect to that measure. In order to use the pluripotential methods, we are led to develop the calculus on positive closed currents. Readers not familiar with these theories may start with the appendix at the end of these notes where we have gathered some notions and results on currents and pluripotential theory. A large part in the appendix is classical but there are also some recent results, mostly on new spaces of currents and on the notion of super-potential associated to positive closed currents in higher bidegree. Since we only deal here with projective spaces and open sets in Ck,thisiseasier and the background is limited. The main problem in the dynamical study of a map is to understand the behavior of the orbits of points under the action of the map. Simple examples show that in general there is a set (Julia set) where the dynamics is unstable: the orbits may di- verge exponentially. Moreover, the geometry of the Julia set is in general very wild. In order to study complex dynamical systems, we follow the classical concepts. We introduce and establish basic properties of some invariants associated to the system, like the topological entropy and the dynamical degrees which are the analogues of volume growth indicators in the real dynamical setting. These invariants give a rough classification of the system. The remarkable fact in complex dynamics is that they can be computed or estimated in many non-trivial situations. Acentralquestionindynamicsistoconstructinterestinginvariantmeasures, in particular, measures with positive entropy. Metric entropy is an indicator of the complexity of the system with respect to an invariant measure. We focus our study on the measure of maximal entropy. Its support is in some sense the most chaotic part of the system. For the maps we consider here, measures of maximal entropy are constructed using pluripotential methods. For endomorphisms in Pk,theycan be obtained as self-intersections of some invariant positive closed (1,1)-currents (Green currents). We give estimates on the Hausdorff dimension and on Lyapounov exponents of these measures. The results give the behavior on the most chaotic part. Lyapounov exponents are shown to be strictly positive. This means in some sense that the system is expansive in all directions, despite of the existence of a critical set. 168 Tien-Cuong Dinh and Nessim Sibony Once, the measure of maximal entropy is constructed,we study its fine dynamical properties. Typical orbits can be observed using test functions. Under the action of the map, each observable provides a sequence of functions that can be seen as dependent random variables. The aim is to show that the dependence is weak and then to establish stochastic properties which are known for independent random variables in probability theory. Mixing, decay of correlations, central limit theorem, large deviations theorems, etc. are proved for the measure of maximal entropy. It is crucial here that the Green currents and the measures of maximal entropy are obtained using an iterative process with estimates; we can then bound the speed of convergence. Another problem, we consider in these notes, is the equidistribution of periodic points or of preimages of points with respect to the measure of maximal entropy.
Load more

Recommended publications
  • Symmetric Rigidity for Circle Endomorphisms with Bounded Geometry
    SYMMETRIC RIGIDITY FOR CIRCLE ENDOMORPHISMS WITH BOUNDED GEOMETRY JOHN ADAMSKI, YUNCHUN HU, YUNPING JIANG, AND ZHE WANG Abstract. Let f and g be two circle endomorphisms of degree d ≥ 2 such that each has bounded geometry, preserves the Lebesgue measure, and fixes 1. Let h fixing 1 be the topological conjugacy from f to g. That is, h ◦ f = g ◦ h. We prove that h is a symmetric circle homeomorphism if and only if h = Id. Many other rigidity results in circle dynamics follow from this very general symmetric rigidity result. 1. Introduction A remarkable result in geometry is the so-called Mostow rigidity theorem. This result assures that two closed hyperbolic 3-manifolds are isometrically equivalent if they are homeomorphically equivalent [18]. A closed hyperbolic 3-manifold can be viewed as the quotient space of a Kleinian group acting on the open unit ball in the 3-Euclidean space. So a homeomorphic equivalence between two closed hyperbolic 3-manifolds can be lifted to a homeomorphism of the open unit ball preserving group actions. The homeomorphism can be extended to the boundary of the open unit ball as a boundary map. The boundary is the Riemann sphere and the boundary map is a quasi-conformal homeomorphism. A quasi-conformal homeomorphism of the Riemann 2010 Mathematics Subject Classification. Primary: 37E10, 37A05; Secondary: 30C62, 60G42. Key words and phrases. quasisymmetric circle homeomorphism, symmetric cir- arXiv:2101.06870v1 [math.DS] 18 Jan 2021 cle homeomorphism, circle endomorphism with bounded geometry preserving the Lebesgue measure, uniformly quasisymmetric circle endomorphism preserving the Lebesgue measure, martingales.
    [Show full text]
  • Generalizations of the Riemann Integral: an Investigation of the Henstock Integral
    Generalizations of the Riemann Integral: An Investigation of the Henstock Integral Jonathan Wells May 15, 2011 Abstract The Henstock integral, a generalization of the Riemann integral that makes use of the δ-fine tagged partition, is studied. We first consider Lebesgue’s Criterion for Riemann Integrability, which states that a func- tion is Riemann integrable if and only if it is bounded and continuous almost everywhere, before investigating several theoretical shortcomings of the Riemann integral. Despite the inverse relationship between integra- tion and differentiation given by the Fundamental Theorem of Calculus, we find that not every derivative is Riemann integrable. We also find that the strong condition of uniform convergence must be applied to guarantee that the limit of a sequence of Riemann integrable functions remains in- tegrable. However, by slightly altering the way that tagged partitions are formed, we are able to construct a definition for the integral that allows for the integration of a much wider class of functions. We investigate sev- eral properties of this generalized Riemann integral. We also demonstrate that every derivative is Henstock integrable, and that the much looser requirements of the Monotone Convergence Theorem guarantee that the limit of a sequence of Henstock integrable functions is integrable. This paper is written without the use of Lebesgue measure theory. Acknowledgements I would like to thank Professor Patrick Keef and Professor Russell Gordon for their advice and guidance through this project. I would also like to acknowledge Kathryn Barich and Kailey Bolles for their assistance in the editing process. Introduction As the workhorse of modern analysis, the integral is without question one of the most familiar pieces of the calculus sequence.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
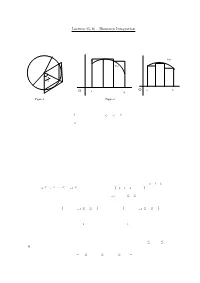
  • Lecture 15-16 : Riemann Integration Integration Is Concerned with the Problem of finding the Area of a Region Under a Curve
    1 Lecture 15-16 : Riemann Integration Integration is concerned with the problem of ¯nding the area of a region under a curve. Let us start with a simple problem : Find the area A of the region enclosed by a circle of radius r. For an arbitrary n, consider the n equal inscribed and superscibed triangles as shown in Figure 1. f(x) f(x) π 2 n O a b O a b Figure 1 Figure 2 Since A is between the total areas of the inscribed and superscribed triangles, we have nr2sin(¼=n)cos(¼=n) · A · nr2tan(¼=n): By sandwich theorem, A = ¼r2: We will use this idea to de¯ne and evaluate the area of the region under a graph of a function. Suppose f is a non-negative function de¯ned on the interval [a; b]: We ¯rst subdivide the interval into a ¯nite number of subintervals. Then we squeeze the area of the region under the graph of f between the areas of the inscribed and superscribed rectangles constructed over the subintervals as shown in Figure 2. If the total areas of the inscribed and superscribed rectangles converge to the same limit as we make the partition of [a; b] ¯ner and ¯ner then the area of the region under the graph of f can be de¯ned as this limit and f is said to be integrable. Let us de¯ne whatever has been explained above formally. The Riemann Integral Let [a; b] be a given interval. A partition P of [a; b] is a ¯nite set of points x0; x1; x2; : : : ; xn such that a = x0 · x1 · ¢ ¢ ¢ · xn¡1 · xn = b.
    [Show full text]
  • Bounded Holomorphic Functions of Several Variables
    Bounded holomorphic functions of several variables Gunnar Berg Introduction A characteristic property of holomorphic functions, in one as well as in several variables, is that they are about as "rigid" as one can demand, without being iden- tically constant. An example of this rigidity is the fact that every holomorphic function element, or germ of a holomorphic function, has associated with it a unique domain, the maximal domain to which the function can be continued. Usually this domain is no longer in euclidean space (a "schlicht" domain), but lies over euclidean space as a many-sheeted Riemann domain. It is now natural to ask whether, given a domain, there is a holomorphic func- tion for which it is the domain of existence, and for domains in the complex plane this is always the case. This is a consequence of the Weierstrass product theorem (cf. [13] p. 15). In higher dimensions, however, the situation is different, and the domains of existence, usually called domains of holomorphy, form a proper sub- class of the class of aU domains, which can be characterised in various ways (holo- morphic convexity, pseudoconvexity etc.). To obtain a complete theory it is also in this case necessary to consider many-sheeted domains, since it may well happen that the maximal domain to which all functions in a given domain can be continued is no longer "schlicht". It is possible to go further than this, and ask for quantitative refinements of various kinds, such as: is every domain of holomorphy the domain of existence of a function which satisfies some given growth condition? Certain results in this direction have been obtained (cf.
    [Show full text]
  • Notes on Metric Spaces
    Notes on Metric Spaces These notes introduce the concept of a metric space, which will be an essential notion throughout this course and in others that follow. Some of this material is contained in optional sections of the book, but I will assume none of that and start from scratch. Still, you should check the corresponding sections in the book for a possibly different point of view on a few things. The main idea to have in mind is that a metric space is some kind of generalization of R in the sense that it is some kind of \space" which has a notion of \distance". Having such a \distance" function will allow us to phrase many concepts from real analysis|such as the notions of convergence and continuity|in a more general setting, which (somewhat) surprisingly makes many things actually easier to understand. Metric Spaces Definition 1. A metric on a set X is a function d : X × X ! R such that • d(x; y) ≥ 0 for all x; y 2 X; moreover, d(x; y) = 0 if and only if x = y, • d(x; y) = d(y; x) for all x; y 2 X, and • d(x; y) ≤ d(x; z) + d(z; y) for all x; y; z 2 X. A metric space is a set X together with a metric d on it, and we will use the notation (X; d) for a metric space. Often, if the metric d is clear from context, we will simply denote the metric space (X; d) by X itself.
    [Show full text]
  • Convergence of Fourier Series
    CONVERGENCE OF FOURIER SERIES KEVIN STEPHEN STOTTER CUDDY Abstract. This paper sets out to explore and explain some of the basic con- cepts of Fourier analysis and its applications. Convolution and questions of convergence will be central. An application to the isoperimetric inequality will conclude the paper. Contents 1. Introduction to Fourier Series 1 2. Convolution and Kernels 2 3. Criteria for Convergence 8 4. Isoperimetric Inequality 18 Acknowledgments 19 References 19 1. Introduction to Fourier Series It will be important for the reader to recall Euler's Formula: ix (1.1) e = cos(x) + i sin(x); 8x 2 R Throughout this paper, an \integrable" function should be interpreted as integrable in the Riemann sense as well as bounded. Definition 1.2. For an integrable, bounded function f :[a; b] ! C we can define, for any integer n, the nth Fourier coefficient 1 Z b f^(n) = f(x)e−2πinx=(b−a)dx: b − a a When there is no question about the function we are referring to we may write ^ P1 ^ 2πinx f(n) = an. From these coefficients we get the Fourier series S(x) = n=−∞ f(n)e (note that this sum may or may not converge). To denote that a Fourier series is associated to a function f we write 1 X f ∼ f^(n)e2πinx n=−∞ Definition 1.3. The N th partial sum of the Fourier series for f, where N is a PN ^ 2πinx=L positive integer, is given by SN (f)(x) = n=−N f(n)e . Date: DEADLINE AUGUST 26, 2012.
    [Show full text]
  • (Sn) Converges to a Real Number S If ∀Ε > 0, ∃Ns.T
    32 MATH 3333{INTERMEDIATE ANALYSIS{BLECHER NOTES 4. Sequences 4.1. Convergent sequences. • A sequence (sn) converges to a real number s if 8 > 0, 9Ns:t: jsn − sj < 8n ≥ N. Saying that jsn−sj < is the same as saying that s− < sn < s+. • If (sn) converges to s then we say that s is the limit of (sn) and write s = limn sn, or s = limn!1 sn, or sn ! s as n ! 1, or simply sn ! s. • If (sn) does not converge to any real number then we say that it diverges. • A sequence (sn) is called bounded if the set fsn : n 2 Ng is a bounded set. That is, there are numbers m and M such that m ≤ sn ≤ M for all n 2 N. This is the same as saying that fsn : n 2 Ng ⊂ [m; M]. It is easy to see that this is equivalent to: there exists a number K ≥ 0 such that jsnj ≤ K for all n 2 N. (See the first lines of the last Section.) Fact 1. Any convergent sequence is bounded. Proof: Suppose that sn ! s as n ! 1. Taking = 1 in the definition of convergence gives that there exists a number N 2 N such that jsn −sj < 1 whenever n ≥ N. Thus jsnj = jsn − s + sj ≤ jsn − sj + jsj < 1 + jsj whenever n ≥ N. Now let M = maxfjs1j; js2j; ··· ; jsN j; 1 + jsjg. We have jsnj ≤ M if n = 1; 2; ··· ;N, and jsnj ≤ M if n ≥ N. So (sn) is bounded. • A sequence (an) is called nonnegative if an ≥ 0 for all n 2 N.
    [Show full text]
  • BAIRE ONE FUNCTIONS 1. History Baire One Functions Are Named in Honor of René-Louis Baire (1874- 1932), a French Mathematician
    BAIRE ONE FUNCTIONS JOHNNY HU Abstract. This paper gives a general overview of Baire one func- tions, including examples as well as several interesting properties involving bounds, uniform convergence, continuity, and Fσ sets. We conclude with a result on a characterization of Baire one func- tions in terms of the notion of first return recoverability, which is a topic of current research in analysis [6]. 1. History Baire one functions are named in honor of Ren´e-Louis Baire (1874- 1932), a French mathematician who had research interests in continuity of functions and the idea of limits [1]. The problem of classifying the class of functions that are convergent sequences of continuous functions was first explored in 1897. According to F.A. Medvedev in his book Scenes from the History of Real Functions, Baire was interested in the relationship between the continuity of a function of two variables in each argument separately and its joint continuity in the two variables [2]. Baire showed that every function of two variables that is continuous in each argument separately is not pointwise continuous with respect to the two variables jointly [2]. For instance, consider the function xy f(x; y) = : x2 + y2 Observe that for all points (x; y) =6 0, f is continuous and so, of course, f is separately continuous. Next, we see that, xy xy lim = lim = 0 (x;0)!(0;0) x2 + y2 (0;y)!(0;0) x2 + y2 as (x; y) approaches (0; 0) along the x-axis and y-axis respectively. However, as (x; y) approaches (0; 0) along the line y = x, we have xy 1 lim = : (x;x)!(0;0) x2 + y2 2 Hence, f is continuous along the lines y = 0 and x = 0, but is discon- tinuous overall at (0; 0).
    [Show full text]
  • Topological Properties of C(X, Y)
    Utah State University DigitalCommons@USU All Graduate Theses and Dissertations Graduate Studies 5-1978 Topological Properties of C(X, Y) Chris Alan Schwendiman Utah State University Follow this and additional works at: https://digitalcommons.usu.edu/etd Part of the Mathematics Commons Recommended Citation Schwendiman, Chris Alan, "Topological Properties of C(X, Y)" (1978). All Graduate Theses and Dissertations. 6949. https://digitalcommons.usu.edu/etd/6949 This Thesis is brought to you for free and open access by the Graduate Studies at DigitalCommons@USU. It has been accepted for inclusion in All Graduate Theses and Dissertations by an authorized administrator of DigitalCommons@USU. For more information, please contact [email protected]. TOPOLOGICALPROPERTIES OF C(X,Y) by Chris Alan Schwendiman A thesis submitted in partial fulfillment of the requirements for the degree of MASTEROF SCIENCE in Mathematics Plan A Approved: UTAHSTATE UNIVERSITY Logan, Utah 1978 ACKNOWLEDGEMENTS I wish to express my many thanks to the members of my committee for their time and effort which they have given me. Their assistance and patience were invaluable in the preparation of this thesis. In particular, I would like to give special thanks to Dr. E. R. Heal who made it possible to study this interesting topic. Chris A. Schwendiman TABLE OF CONTENTS INTRODUCTION. 1 PRELIMIN ARIES 2 PROPERTIES OF C(X,Y) WHENXIS COMPACT 11 PROPERTIES OF C(X,Y) WHENX MAYNOT BE COMPACT 14 REFERENCES 22 VITA 23 ABSTRACT Topological Properties of C(X,Y) by Chris A. Schwendiman, Master of Science Utah State University, 1978 Major Professor: Dr. E. Robert Heal Department: Mathematics The purpose of this paper is to examine the important topological properties of the function spaces BC(X,Y) and C(X,Y).
    [Show full text]
  • Chapter 10 Multivariable Integral
    Chapter 10 Multivariable integral 10.1 Riemann integral over rectangles Note: ??? lectures As in chapter chapter 5, we define the Riemann integral using the Darboux upper and lower inte- grals. The ideas in this section are very similar to integration in one dimension. The complication is mostly notational. The differences between one and several dimensions will grow more pronounced in the sections following. 10.1.1 Rectangles and partitions Definition 10.1.1. Let (a ,a ,...,a ) and (b ,b ,...,b ) be such that a b for all k. A set of 1 2 n 1 2 n k ≤ k the form [a ,b ] [a ,b ] [a ,b ] is called a closed rectangle. In this setting it is sometimes 1 1 × 2 2 ×···× n n useful to allow a =b , in which case we think of [a ,b ] = a as usual. If a <b for all k, then k k k k { k} k k a set of the form(a 1,b 1) (a 2,b 2) (a n,b n) is called an open rectangle. × ×···× n For an open or closed rectangle R:= [a 1,b 1] [a 2,b 2] [a n,b n] R or R:= (a 1,b 1) n × ×···× ⊂ × (a2,b 2) (a n,b n) R , we define the n-dimensional volume by ×···× ⊂ V(R):= (b a )(b a ) (b a ). 1 − 1 2 − 2 ··· n − n A partition P of the closed rectangle R=[a ,b ] [a ,b ] [a ,b ] is afinite set of par- 1 1 × 2 2 ×···× n n titions P1,P2,...,Pn of the intervals [a1,b 1],[a 2,b 2],...,[a n,b n].
    [Show full text]
  • 1. Space of Bounded Functions and Space of Continuous Functions Let X Be a Nonempty Set
    1. Space of Bounded Functions and Space of Continuous functions Let X be a nonempty set. A real-valued function f : X ! R is bounded if there exists M > 0 so that jf(x)j ≤ M; for all x 2 X: The set of bounded real-valued functions on X is denoted by B(X): Given f; g 2 B(X); and a 2 R; we define (f + g)(x) = f(x) + g(x); (af)(x) = af(x) for x 2 X: Proposition 1.1. The set B(X) forms a real vector space. Proof. We leave it to the reader as an exercise. Let V be a real vector space. A norm on V is a function k · k : V ! [0; 1) such that (1) kavk = jajkvk for all a 2 R and v 2 V: (2) kvk = 0 if and only if v = 0: (3) kv + wk ≤ kvk + kwk for v; w 2 V: A normed vector space over R is a real vector space together with a norm. It is easy to see that a norm on V induces a metric on V by d(v; w) = kv − wk: The metric defined above is called the metric induced from the norm. Definition 1.1. A normed vector space over R is called a real Banach space if the space V together with the metric induced from the norm is complete. On B(X); set kfk1 = sup jf(x)j: x2X Definition 1.2. If a sequence ffng converges to f in B(X); we say that ffng converges uniformly to f on X: If ffng converges to f in B(X); by definition, given > 0; there exists N > 0 so that for all n ≥ N; kfn − fk1 < .
    [Show full text]