DOCSLIB.ORG

Complex Analysis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Complex Analysis Complex Analysis Xue-Mei Li May 16, 2016 Contents 1 Complex Differentiation 6 1.1 The Complex Plane . .6 1.2 Complex Functions of One Variables . .6 1.3 Complex Linear Functions . 10 1.4 Complex Differentiation . 10 1.5 The @ and @¯ operator . 13 1.6 Harmonic Functions . 13 1.7 Holomorphic Functions . 14 1.8 Rules of Differentiation . 14 2 The Riemann Sphere and Mobius¨ Transforms 16 2.1 Conformal Mappings . 16 2.2 Mobius¨ Transforms (Lecture 5) . 17 2.2.1 The Extended Complex Plane . 18 2.2.2 Properties of Mobius¨ Transforms . 18 2.3 The Riemann Sphere and Stereographic Projection (lecture 7) . 22 3 Power Series 25 3.1 Power series is holomorphic in its disc of convergence . 25 3.2 Analytic Continuation (Lecture 8) . 27 3.3 The Exponential and Trigonometric Functions . 29 3.4 The Logarithmic Function and Power Function (Lecture 9) . 30 4 Complex Integration 31 4.1 Complex Integration . 31 4.2 Integration Along a Curve (lecture 9) . 32 4.3 Existence of Primitives (Lecture 9) . 34 4.4 Goursat’s Lemma . 37 4.5 Cauchy’s Theorem: simply connected domains (Lecture 12) . 39 4.6 Supplementary . 41 5 Cauchy’s Integral Formula 42 5.1 Keyhole Operation and Other Techniques (Lecture 12) . 42 5.2 Cauchy’s Integral Formula . 44 5.3 Taylor Expansion, Cauchy’s Derivative Formulas . 45 5.4 Estimates, Liouville’s Thm and Morera’s Thm . 46 5.4.1 Supplementary . 48 5.5 Locally Uniform Convergent Sequence of Holomorphic Functions . 48 1 5.6 Schwartz Reflection Principle (Lecture 15) . 49 5.7 The Fundamental Theorem of Algebra . 51 5.8 Zero’s of Analytic Functions . 52 5.9 Uniqueness of Analytic Continuation (Lecture 17) . 55 5.10 Supplementary . 55 6 Laurent Series and Singularities 56 6.1 Laurent Series Development (Lecture 17-18) . 56 6.2 Classification of Isolated Singularities (Lecture 19) . 61 6.2.1 Poles . 62 6.2.2 Essential Singularities . 64 6.3 Meromorphic Function . 64 6.3.1 Supplementary . 64 7 Winding Numbers and the Residue Theorem 66 7.1 The Index of a Closed Curve (Lecture 22) . 67 7.1.1 Supplementary . 69 7.2 The Residue Theorem (Lecture 23) . 71 7.3 Compute Real Integrals . 72 8 Fundamental Theorems 74 8.1 The Argument Principle (Lecture 24) . 74 8.2 Rouche’s´ Theorem . 75 8.2.1 Supplementary . 76 8.3 The Open mapping Theorem (Lecture 25) . 76 8.3.1 Supplementary . 78 8.4 Bi-holomorphic Maps on the Disc (lecture 25-26) . 79 9 The Riemann Mapping Theorem 81 9.1 Hurwitz’s Theorem (lecture 26) . 81 9.2 Family of Holomorphic Functions (Lecture 28) . 82 9.3 The Riemann Mapping Theorem (Lecture 28-29) . 84 9.4 Supplementary . 86 10 Special Functions 87 10.1 Constructing Holomorphic Functions by Integration (Lecture 30) . 87 10.2 The Gamma function . 87 10.3 The zeta function(Lecture 30) . 89 2 Prologue This is the lecture notes for the third year undergraduate module: MA3B8. If you need not be motivated, skip this section. Complex Analysis is concerned with the study of complex number valued functions with complex number as domain. Let f : C ! C be such a function. What can we say about it? Where do we use suchp an analysis? The complex number i = −1 appears in Fourier Transform, an important tool in analysis and engineering, and in the Schrodinger¨ equation, @ 2 @2 i = − ~ + V (x) (t; x); ~ @t 2m @2x a fundamental equation of physics, that describes how a wave function of a physical system evolves. Complex Differentiation is a very important concept, this is allured to by the fact that a number of terminologies are associated with ‘complex differentiable’. A function, complex differentiable on its domain, has two other names: a holomor- phic map and an analytic function, reflecting the original approach. The first meant the function is complex differentiable at every point, and the latter refers to functions with a power series expansion at every point. The beauty is that the two concepts are equivalent. A complex valued function defined on the whole complex domain is an entire function. Quotients of entire functions are Meromorphic functions on the whole plane. A map is conformal at a point if it preserves the angle between two tangent vec- tors at that point. A complex differentiable function is conformal at any point where its derivative does not vanish. Bi-holomorphic functions, a bi-jective holomorphic function between two regions, are conformal in the sense they preserve angles. Of- ten by conformal maps people mean bi-holomorphic maps. Conformal maps are the building blocks in Conformal Field Theory. It is conjectured that 2D statistical mod- els at criticality are conformal invariant. An exciting development is SLE, evolved from the Loewner differential equation describing evolutions of conformal maps. The Schramann-Loewner Evolution (also known as Stochastic Loewner Evolution, abbre- viated as SLE ) has been identified to describe the limits of a number of lattice models in statistical mechanics. Two mathematicians, W. Werner and S. Smirnov, have been awarded the Fields medals for their works on and related to SLE. Complex valued functions are built into the definition for Fourier transforms. For f : R ! R, Z 1 1 −ikx f^(k) = p e dx; k 2 R: 2π 1 Fourier transform extends the concept of Fourier series for period functions, is an im- portant tool in analysis and in image and sound processing, and is widely used in elec- trical engineering. 3 A well known function in number theory is the Riemann zeta-function, 1 X 1 ζ(s) = : ns n=1 The interests in the Riemann-zeta function began with Euler who discovered that the Riemann zeta function can be related to the study of prime numbers. 1 ζ(s) = Π : 1 − p−s The product on the right hand side is over all prime numbers: 1 1 1 1 1 1 1 Π = · · · · ::: :::: 1 − p−s 1 − 2−s 1 − 3−s 1 − 5−s 1 − 7−s 1 − 11−s 1 − p−s The Riemann-zeta function is clearly well defined for s > 1 and extends to all complex numbers except s = 1, a procedure known as the analytic /meromorphic continuation of a real analytic function. Riemann was interested in the following question: how many prime number are below a given number x? Denote this number π(x). Riemann found an explicit formula for π(x) in his 1859 paper in terms of a sum over the zeros of ζ. The Riemann hypothesis states that all non-trivial zeros of the Riemann zeta 1 function lie on the critical line s = 2 . The Clay institute in Canada has offered a prize of 1 million dollars for solving this problem. In symplectic geometry, symplectic manifolds are often studied together with a complex structure. The space C is a role model for symplectic manifold. A 2-dimensional symplectic manifold is a space that looks locally like a piece of R2 and has a symplectic form, which we do not define here. We may impose in addition a complex structure Jx 2 at each point of x 2 M. The complex structure Jx is essentially a matrix s.t. −Jx is the identity and defines a complex structure and leads to the concept of Khaler¨ manifolds. Finally we should mention that complex analysis is an important tool in combina- torial enumeration problems: analysis of analytic or meromorphic generating functions provides means for estimating the coefficients of its series expansions and estimates for the size of discrete structures. Topics Holomorphic Functions, meromorphic functions, poles, zeros, winding numbers (rota- tion number/index) of a closed curve, closed curves homologous to zero, closed curves homotopic to zero, classification of isolated singularities, analytical continuation, Con- formal mappings, Riemann spheres, special functions and maps. Main Theorems: Goursat’s theorem, Cauchy’s theorem, Cauchy’s derivative formulas, Cauchy’s inte- gral formula for curves homologous to zero, Weirerstrass Theorem, The Argument principle, Rouche’s´ theorem, Open Mapping Theorem, Maximum modulus principle, Schwartz’s lemma, Mantel’s Theorem, Hurwitz’s¨ theorem, and the Riemann Mapping Theorem. References • L. V. Ahlfors, Complex Analysis, Third Edition, Mc Graw-Hill, Inc. (1979) 4 • J. B. Conway. Functions of one complex variables. • T. Gamelin. Complex Analysis, Springer. (2001) • E. Hairer, G. Wanner, Analyse Complexe et Series´ de Fourier. http://www.unige.ch/hairer/poly_complexe/complexe.pdf • G. J. O. Jameson. A First course on complex functions. Chapman and Hall, (1970). • E. M. Stein and R. Shakarchi. Complex Analysis. Princeton University Press. (2003) Acknowledgement. I would like to thank E. Hairer and G. Wanner for the figures in this note. 5 Chapter 1 Complex Differentiation 1.1 The Complex Plane The complex plane C = fx+iy : x; y 2 Rg is a field with addition and multiplication, on which is also defined the complex conjugation x + iy = x − iy and modulus (also p p called absolute value) jzj = zz¯ = x2 + y2. It is a vector space over R and over C with the norm jz1 − z2j. We will frequently treat C as a metric space, with distance d(z1; z2) = jz1 − z2j, and so we understand that a sequence of complex numbers zn converges to a complex number z is meant by that the distance jzn − zj converges to zero. The space C with the above mentioned distance is a complete metric space and so a sequence converges if and only if it is a Cauchy sequence. Since 2 2 2 jzn − zj = jRe(zn) − Re(z)j + jIm(zn) − Im(z)j ; zn converges to z if and only if the real parts of (zn) converge to the real part of z and the imaginary parts of (zn) converge to the imaginary part of z.
Load more

Recommended publications
  • Symmetric Rigidity for Circle Endomorphisms with Bounded Geometry
    SYMMETRIC RIGIDITY FOR CIRCLE ENDOMORPHISMS WITH BOUNDED GEOMETRY JOHN ADAMSKI, YUNCHUN HU, YUNPING JIANG, AND ZHE WANG Abstract. Let f and g be two circle endomorphisms of degree d ≥ 2 such that each has bounded geometry, preserves the Lebesgue measure, and fixes 1. Let h fixing 1 be the topological conjugacy from f to g. That is, h ◦ f = g ◦ h. We prove that h is a symmetric circle homeomorphism if and only if h = Id. Many other rigidity results in circle dynamics follow from this very general symmetric rigidity result. 1. Introduction A remarkable result in geometry is the so-called Mostow rigidity theorem. This result assures that two closed hyperbolic 3-manifolds are isometrically equivalent if they are homeomorphically equivalent [18]. A closed hyperbolic 3-manifold can be viewed as the quotient space of a Kleinian group acting on the open unit ball in the 3-Euclidean space. So a homeomorphic equivalence between two closed hyperbolic 3-manifolds can be lifted to a homeomorphism of the open unit ball preserving group actions. The homeomorphism can be extended to the boundary of the open unit ball as a boundary map. The boundary is the Riemann sphere and the boundary map is a quasi-conformal homeomorphism. A quasi-conformal homeomorphism of the Riemann 2010 Mathematics Subject Classification. Primary: 37E10, 37A05; Secondary: 30C62, 60G42. Key words and phrases. quasisymmetric circle homeomorphism, symmetric cir- arXiv:2101.06870v1 [math.DS] 18 Jan 2021 cle homeomorphism, circle endomorphism with bounded geometry preserving the Lebesgue measure, uniformly quasisymmetric circle endomorphism preserving the Lebesgue measure, martingales.
    [Show full text]
  • Generalizations of the Riemann Integral: an Investigation of the Henstock Integral
    Generalizations of the Riemann Integral: An Investigation of the Henstock Integral Jonathan Wells May 15, 2011 Abstract The Henstock integral, a generalization of the Riemann integral that makes use of the δ-fine tagged partition, is studied. We first consider Lebesgue’s Criterion for Riemann Integrability, which states that a func- tion is Riemann integrable if and only if it is bounded and continuous almost everywhere, before investigating several theoretical shortcomings of the Riemann integral. Despite the inverse relationship between integra- tion and differentiation given by the Fundamental Theorem of Calculus, we find that not every derivative is Riemann integrable. We also find that the strong condition of uniform convergence must be applied to guarantee that the limit of a sequence of Riemann integrable functions remains in- tegrable. However, by slightly altering the way that tagged partitions are formed, we are able to construct a definition for the integral that allows for the integration of a much wider class of functions. We investigate sev- eral properties of this generalized Riemann integral. We also demonstrate that every derivative is Henstock integrable, and that the much looser requirements of the Monotone Convergence Theorem guarantee that the limit of a sequence of Henstock integrable functions is integrable. This paper is written without the use of Lebesgue measure theory. Acknowledgements I would like to thank Professor Patrick Keef and Professor Russell Gordon for their advice and guidance through this project. I would also like to acknowledge Kathryn Barich and Kailey Bolles for their assistance in the editing process. Introduction As the workhorse of modern analysis, the integral is without question one of the most familiar pieces of the calculus sequence.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
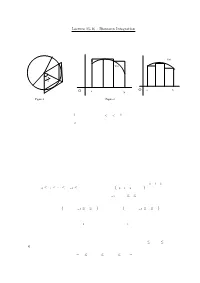
  • Lecture 15-16 : Riemann Integration Integration Is Concerned with the Problem of finding the Area of a Region Under a Curve
    1 Lecture 15-16 : Riemann Integration Integration is concerned with the problem of ¯nding the area of a region under a curve. Let us start with a simple problem : Find the area A of the region enclosed by a circle of radius r. For an arbitrary n, consider the n equal inscribed and superscibed triangles as shown in Figure 1. f(x) f(x) π 2 n O a b O a b Figure 1 Figure 2 Since A is between the total areas of the inscribed and superscribed triangles, we have nr2sin(¼=n)cos(¼=n) · A · nr2tan(¼=n): By sandwich theorem, A = ¼r2: We will use this idea to de¯ne and evaluate the area of the region under a graph of a function. Suppose f is a non-negative function de¯ned on the interval [a; b]: We ¯rst subdivide the interval into a ¯nite number of subintervals. Then we squeeze the area of the region under the graph of f between the areas of the inscribed and superscribed rectangles constructed over the subintervals as shown in Figure 2. If the total areas of the inscribed and superscribed rectangles converge to the same limit as we make the partition of [a; b] ¯ner and ¯ner then the area of the region under the graph of f can be de¯ned as this limit and f is said to be integrable. Let us de¯ne whatever has been explained above formally. The Riemann Integral Let [a; b] be a given interval. A partition P of [a; b] is a ¯nite set of points x0; x1; x2; : : : ; xn such that a = x0 · x1 · ¢ ¢ ¢ · xn¡1 · xn = b.
    [Show full text]
  • Bounded Holomorphic Functions of Several Variables
    Bounded holomorphic functions of several variables Gunnar Berg Introduction A characteristic property of holomorphic functions, in one as well as in several variables, is that they are about as "rigid" as one can demand, without being iden- tically constant. An example of this rigidity is the fact that every holomorphic function element, or germ of a holomorphic function, has associated with it a unique domain, the maximal domain to which the function can be continued. Usually this domain is no longer in euclidean space (a "schlicht" domain), but lies over euclidean space as a many-sheeted Riemann domain. It is now natural to ask whether, given a domain, there is a holomorphic func- tion for which it is the domain of existence, and for domains in the complex plane this is always the case. This is a consequence of the Weierstrass product theorem (cf. [13] p. 15). In higher dimensions, however, the situation is different, and the domains of existence, usually called domains of holomorphy, form a proper sub- class of the class of aU domains, which can be characterised in various ways (holo- morphic convexity, pseudoconvexity etc.). To obtain a complete theory it is also in this case necessary to consider many-sheeted domains, since it may well happen that the maximal domain to which all functions in a given domain can be continued is no longer "schlicht". It is possible to go further than this, and ask for quantitative refinements of various kinds, such as: is every domain of holomorphy the domain of existence of a function which satisfies some given growth condition? Certain results in this direction have been obtained (cf.
    [Show full text]
  • Notes on Metric Spaces
    Notes on Metric Spaces These notes introduce the concept of a metric space, which will be an essential notion throughout this course and in others that follow. Some of this material is contained in optional sections of the book, but I will assume none of that and start from scratch. Still, you should check the corresponding sections in the book for a possibly different point of view on a few things. The main idea to have in mind is that a metric space is some kind of generalization of R in the sense that it is some kind of \space" which has a notion of \distance". Having such a \distance" function will allow us to phrase many concepts from real analysis|such as the notions of convergence and continuity|in a more general setting, which (somewhat) surprisingly makes many things actually easier to understand. Metric Spaces Definition 1. A metric on a set X is a function d : X × X ! R such that • d(x; y) ≥ 0 for all x; y 2 X; moreover, d(x; y) = 0 if and only if x = y, • d(x; y) = d(y; x) for all x; y 2 X, and • d(x; y) ≤ d(x; z) + d(z; y) for all x; y; z 2 X. A metric space is a set X together with a metric d on it, and we will use the notation (X; d) for a metric space. Often, if the metric d is clear from context, we will simply denote the metric space (X; d) by X itself.
    [Show full text]
  • Dynamics in Several Complex Variables: Endomorphisms of Projective Spaces and Polynomial-Like Mappings
    Dynamics in Several Complex Variables: Endomorphisms of Projective Spaces and Polynomial-like Mappings Tien-Cuong Dinh and Nessim Sibony Abstract The emphasis of this introductory course is on pluripotential methods in complex dynamics in higher dimension. They are based on the compactness prop- erties of plurisubharmonic (p.s.h.) functions and on the theory of positive closed currents. Applications of these methods are not limited to the dynamical systems that we consider here. Nervertheless, we choose to show their effectiveness and to describe the theory for two large familiesofmaps:theendomorphismsofprojective spaces and the polynomial-like mappings. The first section deals with holomorphic endomorphisms of the projective space Pk.Weestablishthefirstpropertiesandgive several constructions for the Green currents T p and the equilibrium measure µ = T k. The emphasis is on quantitative properties and speed of convergence. We then treat equidistribution problems. We show the existence of a proper algebraic set E ,totally 1 invariant, i.e. f − (E )=f (E )=E ,suchthatwhena E ,theprobabilitymeasures, n "∈ equidistributed on the fibers f − (a),convergetowardstheequilibriummeasureµ, as n goes to infinity. A similar result holds for the restriction of f to invariant sub- varieties. We survey the equidistribution problem when points are replaced with varieties of arbitrary dimension, and discuss the equidistribution of periodic points. We then establish ergodic properties of µ:K-mixing,exponentialdecayofcorrela- tions for various classes of observables, central limit theorem and large deviations theorem. We heavily use the compactness of the space DSH(Pk) of differences of quasi-p.s.h. functions. In particular, we show that the measure µ is moderate, i.e.
    [Show full text]
  • Convergence of Fourier Series
    CONVERGENCE OF FOURIER SERIES KEVIN STEPHEN STOTTER CUDDY Abstract. This paper sets out to explore and explain some of the basic con- cepts of Fourier analysis and its applications. Convolution and questions of convergence will be central. An application to the isoperimetric inequality will conclude the paper. Contents 1. Introduction to Fourier Series 1 2. Convolution and Kernels 2 3. Criteria for Convergence 8 4. Isoperimetric Inequality 18 Acknowledgments 19 References 19 1. Introduction to Fourier Series It will be important for the reader to recall Euler's Formula: ix (1.1) e = cos(x) + i sin(x); 8x 2 R Throughout this paper, an \integrable" function should be interpreted as integrable in the Riemann sense as well as bounded. Definition 1.2. For an integrable, bounded function f :[a; b] ! C we can define, for any integer n, the nth Fourier coefficient 1 Z b f^(n) = f(x)e−2πinx=(b−a)dx: b − a a When there is no question about the function we are referring to we may write ^ P1 ^ 2πinx f(n) = an. From these coefficients we get the Fourier series S(x) = n=−∞ f(n)e (note that this sum may or may not converge). To denote that a Fourier series is associated to a function f we write 1 X f ∼ f^(n)e2πinx n=−∞ Definition 1.3. The N th partial sum of the Fourier series for f, where N is a PN ^ 2πinx=L positive integer, is given by SN (f)(x) = n=−N f(n)e . Date: DEADLINE AUGUST 26, 2012.
    [Show full text]
  • (Sn) Converges to a Real Number S If ∀Ε > 0, ∃Ns.T
    32 MATH 3333{INTERMEDIATE ANALYSIS{BLECHER NOTES 4. Sequences 4.1. Convergent sequences. • A sequence (sn) converges to a real number s if 8 > 0, 9Ns:t: jsn − sj < 8n ≥ N. Saying that jsn−sj < is the same as saying that s− < sn < s+. • If (sn) converges to s then we say that s is the limit of (sn) and write s = limn sn, or s = limn!1 sn, or sn ! s as n ! 1, or simply sn ! s. • If (sn) does not converge to any real number then we say that it diverges. • A sequence (sn) is called bounded if the set fsn : n 2 Ng is a bounded set. That is, there are numbers m and M such that m ≤ sn ≤ M for all n 2 N. This is the same as saying that fsn : n 2 Ng ⊂ [m; M]. It is easy to see that this is equivalent to: there exists a number K ≥ 0 such that jsnj ≤ K for all n 2 N. (See the first lines of the last Section.) Fact 1. Any convergent sequence is bounded. Proof: Suppose that sn ! s as n ! 1. Taking = 1 in the definition of convergence gives that there exists a number N 2 N such that jsn −sj < 1 whenever n ≥ N. Thus jsnj = jsn − s + sj ≤ jsn − sj + jsj < 1 + jsj whenever n ≥ N. Now let M = maxfjs1j; js2j; ··· ; jsN j; 1 + jsjg. We have jsnj ≤ M if n = 1; 2; ··· ;N, and jsnj ≤ M if n ≥ N. So (sn) is bounded. • A sequence (an) is called nonnegative if an ≥ 0 for all n 2 N.
    [Show full text]
  • BAIRE ONE FUNCTIONS 1. History Baire One Functions Are Named in Honor of René-Louis Baire (1874- 1932), a French Mathematician
    BAIRE ONE FUNCTIONS JOHNNY HU Abstract. This paper gives a general overview of Baire one func- tions, including examples as well as several interesting properties involving bounds, uniform convergence, continuity, and Fσ sets. We conclude with a result on a characterization of Baire one func- tions in terms of the notion of first return recoverability, which is a topic of current research in analysis [6]. 1. History Baire one functions are named in honor of Ren´e-Louis Baire (1874- 1932), a French mathematician who had research interests in continuity of functions and the idea of limits [1]. The problem of classifying the class of functions that are convergent sequences of continuous functions was first explored in 1897. According to F.A. Medvedev in his book Scenes from the History of Real Functions, Baire was interested in the relationship between the continuity of a function of two variables in each argument separately and its joint continuity in the two variables [2]. Baire showed that every function of two variables that is continuous in each argument separately is not pointwise continuous with respect to the two variables jointly [2]. For instance, consider the function xy f(x; y) = : x2 + y2 Observe that for all points (x; y) =6 0, f is continuous and so, of course, f is separately continuous. Next, we see that, xy xy lim = lim = 0 (x;0)!(0;0) x2 + y2 (0;y)!(0;0) x2 + y2 as (x; y) approaches (0; 0) along the x-axis and y-axis respectively. However, as (x; y) approaches (0; 0) along the line y = x, we have xy 1 lim = : (x;x)!(0;0) x2 + y2 2 Hence, f is continuous along the lines y = 0 and x = 0, but is discon- tinuous overall at (0; 0).
    [Show full text]
  • Topological Properties of C(X, Y)
    Utah State University DigitalCommons@USU All Graduate Theses and Dissertations Graduate Studies 5-1978 Topological Properties of C(X, Y) Chris Alan Schwendiman Utah State University Follow this and additional works at: https://digitalcommons.usu.edu/etd Part of the Mathematics Commons Recommended Citation Schwendiman, Chris Alan, "Topological Properties of C(X, Y)" (1978). All Graduate Theses and Dissertations. 6949. https://digitalcommons.usu.edu/etd/6949 This Thesis is brought to you for free and open access by the Graduate Studies at DigitalCommons@USU. It has been accepted for inclusion in All Graduate Theses and Dissertations by an authorized administrator of DigitalCommons@USU. For more information, please contact [email protected]. TOPOLOGICALPROPERTIES OF C(X,Y) by Chris Alan Schwendiman A thesis submitted in partial fulfillment of the requirements for the degree of MASTEROF SCIENCE in Mathematics Plan A Approved: UTAHSTATE UNIVERSITY Logan, Utah 1978 ACKNOWLEDGEMENTS I wish to express my many thanks to the members of my committee for their time and effort which they have given me. Their assistance and patience were invaluable in the preparation of this thesis. In particular, I would like to give special thanks to Dr. E. R. Heal who made it possible to study this interesting topic. Chris A. Schwendiman TABLE OF CONTENTS INTRODUCTION. 1 PRELIMIN ARIES 2 PROPERTIES OF C(X,Y) WHENXIS COMPACT 11 PROPERTIES OF C(X,Y) WHENX MAYNOT BE COMPACT 14 REFERENCES 22 VITA 23 ABSTRACT Topological Properties of C(X,Y) by Chris A. Schwendiman, Master of Science Utah State University, 1978 Major Professor: Dr. E. Robert Heal Department: Mathematics The purpose of this paper is to examine the important topological properties of the function spaces BC(X,Y) and C(X,Y).
    [Show full text]
  • Chapter 10 Multivariable Integral
    Chapter 10 Multivariable integral 10.1 Riemann integral over rectangles Note: ??? lectures As in chapter chapter 5, we define the Riemann integral using the Darboux upper and lower inte- grals. The ideas in this section are very similar to integration in one dimension. The complication is mostly notational. The differences between one and several dimensions will grow more pronounced in the sections following. 10.1.1 Rectangles and partitions Definition 10.1.1. Let (a ,a ,...,a ) and (b ,b ,...,b ) be such that a b for all k. A set of 1 2 n 1 2 n k ≤ k the form [a ,b ] [a ,b ] [a ,b ] is called a closed rectangle. In this setting it is sometimes 1 1 × 2 2 ×···× n n useful to allow a =b , in which case we think of [a ,b ] = a as usual. If a <b for all k, then k k k k { k} k k a set of the form(a 1,b 1) (a 2,b 2) (a n,b n) is called an open rectangle. × ×···× n For an open or closed rectangle R:= [a 1,b 1] [a 2,b 2] [a n,b n] R or R:= (a 1,b 1) n × ×···× ⊂ × (a2,b 2) (a n,b n) R , we define the n-dimensional volume by ×···× ⊂ V(R):= (b a )(b a ) (b a ). 1 − 1 2 − 2 ··· n − n A partition P of the closed rectangle R=[a ,b ] [a ,b ] [a ,b ] is afinite set of par- 1 1 × 2 2 ×···× n n titions P1,P2,...,Pn of the intervals [a1,b 1],[a 2,b 2],...,[a n,b n].
    [Show full text]