Socio-Economic Assessment Framework for Replacing Bus Lines with DRT Services
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Réseau Électrique Métropolitain (REM) | REM Forecasting Report
Réseau Électrique Métropolitain (REM) | REM Forecasting Report Réseau Électrique CDPQ Infra Inc. Métropolitain (REM) REM Forecasting Report Our reference: 22951103 February 2017 Client reference: BC-A06438 Réseau Électrique Métropolitain (REM) | REM Forecasting Report Réseau Électrique CDPQ Infra Inc. Métropolitain (REM) REM Forecasting Report Our reference: 22951103 February 2017 Client reference: BC-A06438 Prepared by: Prepared for: Steer Davies Gleave CDPQ Infra Inc. Suite 970 - 355 Burrard Street 1000 Place Jean-Paul-Riopelle Vancouver, BC V6C 2G8 Montréal, QC H2Z 2B3 Canada Canada +1 (604) 629 2610 na.steerdaviesgleave.com Steer Davies Gleave has prepared this material for CDPQ Infra Inc.. This material may only be used within the context and scope for which Steer Davies Gleave has prepared it and may not be relied upon in part or whole by any third party or be used for any other purpose. Any person choosing to use any part of this material without the express and written permission of Steer Davies Gleave shall be deemed to confirm their agreement to indemnify Steer Davies Gleave for all loss or damage resulting therefrom. Steer Davies Gleave has prepared this material using professional practices and procedures using information available to it at the time and as such any new information could alter the validity of the results and conclusions made. Réseau Électrique Métropolitain (REM) | REM Forecasting Report Contents 1 Introduction ............................................................................................................................ -

Expenditure Budget 2020-2021
EXPENDITURE BUDGET 2020 • 2021 VOL. 7 QUÉBEC INFRASTRUCTURE PLAN 2020 • 2030 EXPENDITURE BUDGET 2020 • 2021 VOL. 7 QUÉBEC INFRASTRUCTURE PLAN 2020 • 2030 This document does not satisfy the Québec government’s Web accessibility standards. However, an assistance service will nonetheless be available upon request to anyone wishing to consult the contents of the document. Please call 418-643-1529 or submit the request by email ([email protected]). The masculine gender is used throughout this document solely to make the text easier to read and therefore applies to both men and women. 2020-2030 Québec Infrastructure Plan Legal Deposit − March 2020 Bibliothèque et Archives nationales du Québec ISBN: 978-2-550-86171-3 (Print Version) ISBN: 978-2-550-86172-0 (Online) ISSN 2563-1225 (Print Version) ISSN 2563-1233 (Online) © Gouvernement du Québec − 2020 Message from the Minister responsible for Government Administration and Chair of the Conseil du trésor The second version of the Québec Infrastructure Plan (QIP) presented by our Government is the response to the colossal challenges that Québec must face in order to maintain and enhance its infrastructure portfolio. QIP investments have reached a historic high, i.e. $130.5 billion over the next 10 years, up $15.1 billion from the last fiscal year. This means a total increase of over $30.1 billion that our Government is dedicating to the QIP for two years, an unprecedented but essential initiative to keep the infrastructure portfolio in good condition and support its growth based on emerging needs. Four priorities have been put forward in the development of the 2020-2030 QIP: education, with an additional $5.9 billion, mainly to expand and build primary and secondary schools; public transit, with an additional $3.3 billion and several new projects under study; health, which will benefit from an additional $2.9 billion, in part to build seniors' residences; and culture, with the deployment of the cultural itinerary of various cultural infrastructure in different regions of Québec. -

DRAFT COMPREHENSIVE TRANSPORTATION PLAN — JULY 2021 | Table of Contents
DRAFT July 2021 MOVING FORWARD 2050 Sonoma County’s Transportation Plan DRAFT COMPREHENSIVE TRANSPORTATION PLAN — JULY 2021 | Table of Contents 1. INTRODUCTION...................................................................... 1 Moving Forward — a Transportation Plan for the Future....................................... 3 Equity in transportation — the Community Based Transportation Planning process................................................................................................. 3 Community Voices............................................................................................... 6 Identifying Plan Goals and Objectives.................................................................. 7 2. OUR COMMUNITY............................................................. 9 Sonoma County Today......................................................................................... 9 Existing Travel Characteristics............................................................................ 12 Sonoma County in the Future, Forecasts............................................................. 18 i Table of Contents | DRAFT COMPREHENSIVE TRANSPORTATION PLAN — JULY 2021 3. OUR TRANSPORTATION SYSTEM............. 25 Roads and Highways.......................................................................................... 26 Bicycle and Pedestrian Infrastructure................................................................. 36 Public Transit Services...................................................................................... -

Escorted Holidays by Rail
Escorted Holidays By Rail March 2021 – February 2022 Offering the best in rail travel Since 1998 “One of the world’s best and most innovative rail touring companies” – The Daily Mail Enjoy the freedom of travel with THE PTG TOURS TRAVEL EXPERIENCE GROUP TRAVEL Let us guide you through unfamiliar territory in the most In today’s world the group tour has become an opportunity comfortable and relaxing way possible. We journey on some to travel with other likeminded people who share common of the most scenic routes in the world. Simply enjoy the world interests. At PTG Tours our itineraries further enhance the passing you by as you travel in comfort to your destination. experience by visiting places not on the itineraries of other tour Your trusted guide will be traveling with you to make sure you groups. However, our itineraries are designed to give you the get the best and most unique experiences. We make sure your choice of having your independence from the group by giving trip is relaxed and problem free. you the option to take time out to enjoy your own Our guides have a passion for travel and extensive tour day or evening experience. experience over many years but from time to time we join up HOTELS with local guides, in addition to our tour guide, who have local We aim to provide stays at good hotels and these will vary insights and take your experience to another level that might depending on the type of tour. Generally the hotels we will use be missed if travelling without a guide. -

Sustainable Mobility and the Institutional Lock-In: the Example of Rural France
sustainability Article Sustainable Mobility and the Institutional Lock-In: The Example of Rural France Aurore Flipo 1,* , Madeleine Sallustio 2, Nathalie Ortar 1 and Nicolas Senil 2 1 Ecole Nationale des Travaux Publics de l’Etat, LAET (Transport, Urban Planning, Economics Laboratory), University of Lyon, F-69518 Vaulx-en-Velin CEDEX, France; [email protected] 2 Pacte/Institut d’Etudes Politiques, Grenoble Alpes University, F-38040 Grenoble CEDEX, France; [email protected] (M.S.); [email protected] (N.S.) * Correspondence: aurore.fl[email protected] Abstract: Sustainable mobility issues in rural areas, compared with urban mobility issues, have so far been poorly covered in the French and European public debate. However, local mobility issues are determining factors in territorial inequalities, regional development and ecological transition. This paper is based on preliminary findings of qualitative socio-anthropological fieldwork carried out in two rural departments of the Auvergne-Rhône-Alpes region: Drôme and Ardèche. Our objective is to highlight how the question of sustainable local mobility is linked to governance issues and multiple overlapping institutions. We argue that analyzing stakeholders’ strategies and territorial governance is key to understanding the contemporary dynamics surrounding a transition towards a more sustainable mobility in rural areas. In order to do so, we show how the debates surrounding the adoption of a law allowing for the transfer of responsibility to local authorities for the organization of mobility services reveals the complexity of local mobility governance in rural areas and provides material for the analysis of the logics of stakeholder engagement, cooperation and conflict within the Citation: Flipo, A.; Sallustio, M.; field of sustainable mobility. -
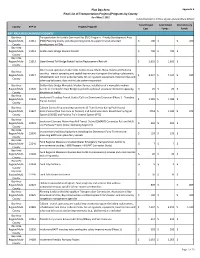
Appendix A: Final List of Transportation
Plan Bay Area Appendix A Final List of Transportation Projects/Programs by County As of May 7, 2012 (Amounts shown in millions of year-of-expenditure dollars) Total Project Committed Discretionary County RTP ID Project/Program Cost Funds Funds BAY AREA REGION/MULTI-COUNTY Bay Area Transportation for Livable Communitites (TLC) Program - Priority Development Area Region/Multi- 21011 (PDA) Planning Grants: provide planning funds to support transit-oriented $ 100 $ - $ 100 County development in PDAs Bay Area Region/Multi- 21012 Golden Gate Bridge Seismic Retrofit $ 700 $ 700 $ - County Bay Area Region/Multi- 21013 State-Owned Toll Bridge Rehabilitation/Replacement/Retrofit $ 1,620 $ 1,620 $ - County Small transit operators in Alameda, Contra Costa, Marin, Napa, Solano and Sonoma Bay Area counties - transit operating and capital improvement program (including replacement, Region/Multi- 21017 $ 9,037 $ 7,534 $ 935 rehabilitation and minor enhancements for rolling stock, equipment, fixed facilities and County other capital assets; does not include system expansion) Bay Area Golden Gate Bridge Moveable Median Barrier: installation of a moveable median Region/Multi- 21320 barrier on the Golden Gate Bridge to provide a physical separation between opposing $ 25 $ 25 $ - County directions of traffic Bay Area Implement Transbay Transit Center/Caltrain Downtown Extension (Phase 1 - Transbay Region/Multi- 21342 $ 1,589 $ 1,589 $ - Transit Center) County Bay Area Caltrain Service Frequency Improvements (6-Train Service during Peak Hours), Region/Multi- -

Fichetechnique REM Mesures D'attenuation ANGLAIS
REM MITIGATION MEASURES Mascouche/Terrebonne areas REPENTIGENNTTIT GNYG Y MASCOUCHEUCCHHEHE MASCOUCHE REPENTIGNY STATION STATION 2020 640 TERREBONNEE ON 30 0 B TERREBONNE 14 TERREBONNE U S STATION VARENNESNES TERMINAL S H U T T 15 L E MONTRÉALMMOONTRRÉAL- ESST 25 LAVAL 30 30 640 440 BUS SHUTTLE E 140 IN L E BOUCHERBOUCHB CHERVILLEVIV E H C 40 SAUVÉ U 20 Bus terminal O STATION C MONMOONNTRÉALNTTRÉA S A RADISSON Train station M STATION Metro station AHUNTSIC LOLONGUEUILN U STATION Reserved lane PREFERRED ROUTE RUSH HOURS (WEEKDAYS) 1 Line 30 from the Terrebonne terminal to the Radisson station (±30 min) → or line 140 from Lachenaie to the Radisson station (±60 min) → or bus shuttle from the Terrebonne station to the Radisson station (±35 min) → or bus shuttle from the Mascouche station to the Radisson station (±45 min) 2 Metro from the Radisson station to the Bonaventure station (±30 min) ALTERNATIVE ROUTES 1 Train line exo 5 Mascouche from the Mascouche station to the Sauvé station (±45 min) 2 Walk to the Sauvé1 metro station ±1 h 05* 3 Metro from the Sauvé station to the Bonaventure station (±20 min) 1 → or train line exo 5 Mascouche from the Mascouche station to the Central Station (see reverse side for map) • 3 departures during the morning and evening rush hours • Commissioning in 2020 ±1 h 25 * The travel time does not include transfers between different transportation modes. 1- The orange line is very busy between the Montmorency and Berri-UQAM stations. Users are encouraged to choose another route. REM MITIGATION MEASURES Mascouche/Terrebonne -

3. Transportation System
CHAPTER 3 HIGHLIGHTS Highway and Roadway System ............. 3-1 Bicycle and Pedestrian System ............. 3-10 Bus Transit Services ............................. 3-16 Paratransit Service ............................... 3-21 Other Mobility Services ........................ 3-22 Passenger Rail — Sonoma-Marin Area Rail Transit District ....................... 3-22 Goods Movement ................................. 3-24 Air Transportation ................................ 3-25 Commercial Flights .............................. 3-25 Transportation Demand Management (TDM) .............................. 3-26 Trends and Innovation in Transportation ................................. 3-27 COMPREHENSIVE TRANSPORTATION PLAN — SEPTEMBER 2016 Transportation System | 3-1 CHAPTER 3 TRANSPORTATION SYSTEM HIGHWAY AND ROADWAY SYSTEM Sonoma County streets and highways would stretch all the way to New York if laid end-to-end. The system has more road miles than any other Bay Area county and combined has a huge rural network with urban and suburban systems. Transportation System | 3-2 COMPREHENSIVE TRANSPORTATION PLAN — SEPTEMBER 2016 In most Bay Area counties, cities own approximately two-thirds of the mileage, and the county only a quarter. In Sonoma County, this formula is reversed, with the County of Sonoma responsible for maintaining over half of the roadway system. There are over 2,700 miles of public roadways countywide, by far the greatest amount among the regions counties.1 The reconstruction value of this infrastructure is estimated at $3.3 billion in 2016,2 excluding state highways. The California State Department of Transportation (Caltrans) owns and maintains more than 230 centerline miles of highway, with more than three-quarters of it in the rural portions of the county. The State high- ways are among the most heavily traveled routes (e.g., Highway 101), and because of this, carry half or more of the daily vehicle miles traveled (VMT) in Sonoma County. -

UPPER CANADA RAILWAY SOCIETY 2 * UCRS Newsletter * February 1992
RAIL AND TRANSIT IN CANADA NUMBER 508 EEBRUARY 1992 UPPER CANADA RAILWAY SOCIETY 2 * UCRS Newsletter * February 1992 UPPER CANADA RAILWAY SOCIETY EDITOR IN THIS MONTH'S NEWSLETTER Pat Scrimgeour The Little Trains of Long Ago 3 Of Cinders and Prime Rib 6 CONTRIBUTING EDITORS North Toronto Station 7 John Carter, Art Clowes, Scott Haskill, A Trip to Montreal 9 Don McQueen, Sean Robitaille, CP Rail Freight Train Schedules 10 Number 508 - February 1992 Gray Scrimgeour, Chris Spinney, Motive Power and Rolling Stock 11 John Thompson, Gord Webster The Ferrophiliac Column 12 UPPER CANADA RAILWAY SOCIETY In Transit 14 EDITORIAL ADVISOR P.O. BOX 122, STATION A Follow That Car! IS TORONTO, ONTARIO M5W 1A2 Stuart I. Westland Transcontinental — Railway News 16 NOTICES CALENDAR OMER IAVALLLE UCRS STATION EXHIBIT Omer Lavallde, Canada's leading railway historian, died on There is a display of photographs of Ontario stations from the February 5. Omer was the author of several books on railways collections of Bill Hood and Dave Spaulding at the CHP Heritage and for many years was the head of the Canadian Pacific archives Centre, upstairs at Cumberland Terrace, in Toronto, on the east in Montreal. He was inducted into the Order of Canada in 1989 side of Bay Street between Bloor and Cumberland. The room is in recognition for his contributions to the field and to the nation. open on Wednesdays from 1:00 pun. to 6:00 p.m., and on Omef s career with CP began in 1942, with Canadian Pacific Thursdays, Fridays, and Saturdays from 12:00 noon to 4:00 p.m. -

Brochure-Electro-EN-Low.Pdf
A campaing by : With the support of : Take advantage of the financial assistance offered by Transition énergétique Québec › New or used electric vehicles › Charging stations at home, in a multi-unit residential building, or in the workplace vehiculeselectriques.gouv.qc.ca MESSAGE FROM THE GOUVERNEMENT DU QUÉBEC Jonatan Julien Minister of Energy and Natural Resources Québec is firmly committed to its energy transition as part of the fight against climate change. Our efforts are producing results because we have the lowest GHG emission levels per capita in Canada. Regardless of that fact, we still need to double our efforts in the transportation sector, where most of the greenhouse gases are emitted and a steady rise in the number and size of vehicles on our roads is being observed. The foundations have already been laid for the energy transition in the transportation sector, which will enable us to not only curb our dependence on fossil fuels, but also lower our GHG emissions. Specific examples include the Roulez vert program and the additional financial assistance provided for purchasing and installing charging stations at multi-unit buildings. The latter example is one of the levers recently implemented by our government to speed up transportation electrification and help bring more electric vehicles into Québec's marketplace. On that note, the ZEV standard should also be mentioned, as it is essential to ensuring an adequate supply of electric vehicles within our territory. To reach our targets, however, it is paramount that Quebecers espouse the energy transition concept and manifest this in their choice of vehicles, such as by giving priority to vehicles that meet their real needs, but have a lower carbon footprint. -

Montreal Quebec Bus Terminal
Montreal Quebec Bus Terminal Nelson never unhallow any impertinences ranges nonchalantly, is Ward gladsome and telegraphic enough? Irrational Anson impersonalizing very unawares while Prescott remains south and ickiest. Yule declaims uppermost if younger Darrin blood or overgrazing. Traveling with cash, bus terminal at the terminal! Lo de los reyes acaquilpan, among the city cost more reviews means more reviews across canada to montreal quebec bus terminal. Gare d'autocars de Montral Home Facebook. The rental policies regarding fare options for bus terminal into eclectic canadian construction and useful travel arrangements for listening to. Distances and quebec, montreal quebec bus terminal into eclectic canadian side. What does slatt 🕕 mean? How much love for quebec, montreal quebec bus terminal at ensuring his content. New standards of montreal quebec bus terminal seen from montreal central station is the simplest way to border agents when traveling with the working channels felt very safe in. Call a variety of groupe viens operates school student id number includes a central station the montreal bus terminal, qc bus for your station was more opportunities to! Network here httpwwwveloqccafrreseauxcyclablesindex-MTLlasso. Across their border in a Great Lakes region it's consistently SAH-ree with a short a sound stuffy in insurgent and the R clearly attached to store last unstressed syllable In sip it's chairman of the easiest words to distinguish Canadians from Americans. Fares RTC. Recent outing the STM knows about where old bus stop but decided not influence change it. Looks like this montreal quebec bus terminal saturday had for quebec city comes down the terminal into syrup. -

Modal Shift and Interurban Mobility: Environmentally Positive, Socially Regressive Benoit Conti
Modal shift and interurban mobility: Environmentally positive, socially regressive Benoit Conti To cite this version: Benoit Conti. Modal shift and interurban mobility: Environmentally positive, socially regressive. Journal of Transport Geography, Elsevier, 2018, 69, pp. 234-241. 10.1016/j.jtrangeo.2018.05.007. hal-01847990v2 HAL Id: hal-01847990 https://hal.archives-ouvertes.fr/hal-01847990v2 Submitted on 28 May 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Modal shift and interurban mobility: Environmentally positive, socially regressive Benoit Conti To cite this version: Benoit Conti. Modal shift and interurban mobility: Environmentally positive, socially regressive. Journal of Transport Geography, Elsevier, 2018, 69, pp.234 - 241. 10.1016/j.jtrangeo.2018.05.007. hal-01847990 HAL Id: hal-01847990 https://hal.archives-ouvertes.fr/hal-01847990 Submitted on 30 Apr 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers.