Mathematical Visualization
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Hydraulic Cylinder Replacement for Cylinders with 3/8” Hydraulic Hose Instructions
HYDRAULIC CYLINDER REPLACEMENT FOR CYLINDERS WITH 3/8” HYDRAULIC HOSE INSTRUCTIONS INSTALLATION TOOLS: INCLUDED HARDWARE: • Knife or Scizzors A. (1) Hydraulic Cylinder • 5/8” Wrench B. (1) Zip-Tie • 1/2” Wrench • 1/2” Socket & Ratchet IMPORTANT: Pressure MUST be relieved from hydraulic system before proceeding. PRESSURE RELIEF STEP 1: Lower the Power-Pole Anchor® down so the Everflex™ spike is touching the ground. WARNING: Do not touch spike with bare hands. STEP 2: Manually push the anchor into closed position, relieving pressure. Manually lower anchor back to the ground. REMOVAL STEP 1: Remove the Cylinder Bottom from the Upper U-Channel using a 1/2” socket & wrench. FIG 1 or 2 NOTE: For Blade models, push bottom of cylinder up into U-Channel and slide it forward past the Ram Spacers to remove it. Upper U-Channel Upper U-Channel Cylinder Bottom 1/2” Tools 1/2” Tools Ram 1/2” Tools Spacers Cylinder Bottom If Ram-Spacers fall out Older models have (1) long & (1) during removal, push short Ram Spacer. Ram Spacers 1/2” Tools bushings in to hold MUST be installed on the same side Figure 1 Figure 2 them in place. they were removed. Blade Models Pro/Spn Models Need help? Contact our Customer Service Team at 1 + 813.689.9932 Option 2 HYDRAULIC CYLINDER REPLACEMENT FOR CYLINDERS WITH 3/8” HYDRAULIC HOSE INSTRUCTIONS STEP 2: Remove the Cylinder Top from the Lower U-Channel using a 1/2” socket & wrench. FIG 3 or 4 Lower U-Channel Lower U-Channel 1/2” Tools 1/2” Tools Cylinder Top Cylinder Top Figure 3 Figure 4 Blade Models Pro/SPN Models STEP 3: Disconnect the UP Hose from the Hydraulic Cylinder Fitting by holding the 1/2” Wrench 5/8” Wrench Cylinder Fitting Base with a 1/2” wrench and turning the Hydraulic Hose Fitting Cylinder Fitting counter-clockwise with a 5/8” wrench. -

Examples of Manifolds
Examples of Manifolds Example 1 (Open Subset of IRn) Any open subset, O, of IRn is a manifold of dimension n. One possible atlas is A = (O, ϕid) , where ϕid is the identity map. That is, ϕid(x) = x. n Of course one possible choice of O is IR itself. Example 2 (The Circle) The circle S1 = (x,y) ∈ IR2 x2 + y2 = 1 is a manifold of dimension one. One possible atlas is A = {(U , ϕ ), (U , ϕ )} where 1 1 1 2 1 y U1 = S \{(−1, 0)} ϕ1(x,y) = arctan x with − π < ϕ1(x,y) <π ϕ1 1 y U2 = S \{(1, 0)} ϕ2(x,y) = arctan x with 0 < ϕ2(x,y) < 2π U1 n n n+1 2 2 Example 3 (S ) The n–sphere S = x =(x1, ··· ,xn+1) ∈ IR x1 +···+xn+1 =1 n A U , ϕ , V ,ψ i n is a manifold of dimension . One possible atlas is 1 = ( i i) ( i i) 1 ≤ ≤ +1 where, for each 1 ≤ i ≤ n + 1, n Ui = (x1, ··· ,xn+1) ∈ S xi > 0 ϕi(x1, ··· ,xn+1)=(x1, ··· ,xi−1,xi+1, ··· ,xn+1) n Vi = (x1, ··· ,xn+1) ∈ S xi < 0 ψi(x1, ··· ,xn+1)=(x1, ··· ,xi−1,xi+1, ··· ,xn+1) n So both ϕi and ψi project onto IR , viewed as the hyperplane xi = 0. Another possible atlas is n n A2 = S \{(0, ··· , 0, 1)}, ϕ , S \{(0, ··· , 0, −1)},ψ where 2x1 2xn ϕ(x , ··· ,xn ) = , ··· , 1 +1 1−xn+1 1−xn+1 2x1 2xn ψ(x , ··· ,xn ) = , ··· , 1 +1 1+xn+1 1+xn+1 are the stereographic projections from the north and south poles, respectively. -

Simple Infinite Presentations for the Mapping Class Group of a Compact
SIMPLE INFINITE PRESENTATIONS FOR THE MAPPING CLASS GROUP OF A COMPACT NON-ORIENTABLE SURFACE RYOMA KOBAYASHI Abstract. Omori and the author [6] have given an infinite presentation for the mapping class group of a compact non-orientable surface. In this paper, we give more simple infinite presentations for this group. 1. Introduction For g ≥ 1 and n ≥ 0, we denote by Ng,n the closure of a surface obtained by removing disjoint n disks from a connected sum of g real projective planes, and call this surface a compact non-orientable surface of genus g with n boundary components. We can regard Ng,n as a surface obtained by attaching g M¨obius bands to g boundary components of a sphere with g + n boundary components, as shown in Figure 1. We call these attached M¨obius bands crosscaps. Figure 1. A model of a non-orientable surface Ng,n. The mapping class group M(Ng,n) of Ng,n is defined as the group consisting of isotopy classes of all diffeomorphisms of Ng,n which fix the boundary point- wise. M(N1,0) and M(N1,1) are trivial (see [2]). Finite presentations for M(N2,0), M(N2,1), M(N3,0) and M(N4,0) ware given by [9], [1], [14] and [16] respectively. Paris-Szepietowski [13] gave a finite presentation of M(Ng,n) with Dehn twists and arXiv:2009.02843v1 [math.GT] 7 Sep 2020 crosscap transpositions for g + n > 3 with n ≤ 1. Stukow [15] gave another finite presentation of M(Ng,n) with Dehn twists and one crosscap slide for g + n > 3 with n ≤ 1, applying Tietze transformations for the presentation of M(Ng,n) given in [13]. -

An Introduction to Topology the Classification Theorem for Surfaces by E
An Introduction to Topology An Introduction to Topology The Classification theorem for Surfaces By E. C. Zeeman Introduction. The classification theorem is a beautiful example of geometric topology. Although it was discovered in the last century*, yet it manages to convey the spirit of present day research. The proof that we give here is elementary, and its is hoped more intuitive than that found in most textbooks, but in none the less rigorous. It is designed for readers who have never done any topology before. It is the sort of mathematics that could be taught in schools both to foster geometric intuition, and to counteract the present day alarming tendency to drop geometry. It is profound, and yet preserves a sense of fun. In Appendix 1 we explain how a deeper result can be proved if one has available the more sophisticated tools of analytic topology and algebraic topology. Examples. Before starting the theorem let us look at a few examples of surfaces. In any branch of mathematics it is always a good thing to start with examples, because they are the source of our intuition. All the following pictures are of surfaces in 3-dimensions. In example 1 by the word “sphere” we mean just the surface of the sphere, and not the inside. In fact in all the examples we mean just the surface and not the solid inside. 1. Sphere. 2. Torus (or inner tube). 3. Knotted torus. 4. Sphere with knotted torus bored through it. * Zeeman wrote this article in the mid-twentieth century. 1 An Introduction to Topology 5. -

Volumes of Prisms and Cylinders 625
11-4 11-4 Volumes of Prisms and 11-4 Cylinders 1. Plan Objectives What You’ll Learn Check Skills You’ll Need GO for Help Lessons 1-9 and 10-1 1 To find the volume of a prism 2 To find the volume of • To find the volume of a Find the area of each figure. For answers that are not whole numbers, round to prism a cylinder the nearest tenth. • To find the volume of a 2 Examples cylinder 1. a square with side length 7 cm 49 cm 1 Finding Volume of a 2. a circle with diameter 15 in. 176.7 in.2 . And Why Rectangular Prism 3. a circle with radius 10 mm 314.2 mm2 2 Finding Volume of a To estimate the volume of a 4. a rectangle with length 3 ft and width 1 ft 3 ft2 Triangular Prism backpack, as in Example 4 2 3 Finding Volume of a Cylinder 5. a rectangle with base 14 in. and height 11 in. 154 in. 4 Finding Volume of a 6. a triangle with base 11 cm and height 5 cm 27.5 cm2 Composite Figure 7. an equilateral triangle that is 8 in. on each side 27.7 in.2 New Vocabulary • volume • composite space figure Math Background Integral calculus considers the area under a curve, which leads to computation of volumes of 1 Finding Volume of a Prism solids of revolution. Cavalieri’s Principle is a forerunner of ideas formalized by Newton and Leibniz in calculus. Hands-On Activity: Finding Volume Explore the volume of a prism with unit cubes. -

The Sphere Project
;OL :WOLYL 7YVQLJ[ +XPDQLWDULDQ&KDUWHUDQG0LQLPXP 6WDQGDUGVLQ+XPDQLWDULDQ5HVSRQVH ;OL:WOLYL7YVQLJ[ 7KHULJKWWROLIHZLWKGLJQLW\ ;OL:WOLYL7YVQLJ[PZHUPUP[PH[P]L[VKL[LYTPULHUK WYVTV[LZ[HUKHYKZI`^OPJO[OLNSVIHSJVTT\UP[` /\THUP[HYPHU*OHY[LY YLZWVUKZ[V[OLWSPNO[VMWLVWSLHMMLJ[LKI`KPZHZ[LYZ /\THUP[HYPHU >P[O[OPZ/HUKIVVR:WOLYLPZ^VYRPUNMVYH^VYSKPU^OPJO [OLYPNO[VMHSSWLVWSLHMMLJ[LKI`KPZHZ[LYZ[VYLLZ[HISPZO[OLPY *OHY[LYHUK SP]LZHUKSP]LSPOVVKZPZYLJVNUPZLKHUKHJ[LK\WVUPU^H`Z[OH[ YLZWLJ[[OLPY]VPJLHUKWYVTV[L[OLPYKPNUP[`HUKZLJ\YP[` 4PUPT\T:[HUKHYKZ This Handbook contains: PU/\THUP[HYPHU (/\THUP[HYPHU*OHY[LY!SLNHSHUKTVYHSWYPUJPWSLZ^OPJO HUK YLÅLJ[[OLYPNO[ZVMKPZHZ[LYHMMLJ[LKWVW\SH[PVUZ 4PUPT\T:[HUKHYKZPU/\THUP[HYPHU9LZWVUZL 9LZWVUZL 7YV[LJ[PVU7YPUJPWSLZ *VYL:[HUKHYKZHUKTPUPT\TZ[HUKHYKZPUMV\YRL`SPMLZH]PUN O\THUP[HYPHUZLJ[VYZ!>H[LYZ\WWS`ZHUP[H[PVUHUKO`NPLUL WYVTV[PVU"-VVKZLJ\YP[`HUKU\[YP[PVU":OLS[LYZL[[SLTLU[HUK UVUMVVKP[LTZ"/LHS[OHJ[PVU;OL`KLZJYPILwhat needs to be achieved in a humanitarian response in order for disaster- affected populations to survive and recover in stable conditions and with dignity. ;OL:WOLYL/HUKIVVRLUQV`ZIYVHKV^ULYZOPWI`HNLUJPLZHUK PUKP]PK\HSZVMMLYPUN[OLO\THUP[HYPHUZLJ[VYH common language for working together towards quality and accountability in disaster and conflict situations ;OL:WOLYL/HUKIVVROHZHU\TILYVMºJVTWHUPVU Z[HUKHYKZ»L_[LUKPUNP[ZZJVWLPUYLZWVUZL[VULLKZ[OH[ OH]LLTLYNLK^P[OPU[OLO\THUP[HYPHUZLJ[VY ;OL:WOLYL7YVQLJ[^HZPUP[PH[LKPU I`HU\TILY VMO\THUP[HYPHU5.6ZHUK[OL9LK*YVZZHUK 9LK*YLZJLU[4V]LTLU[ ,+0;065 7KHB6SKHUHB3URMHFWBFRYHUBHQBLQGG The Sphere Project Humanitarian Charter and Minimum Standards in Humanitarian Response Published by: The Sphere Project Copyright@The Sphere Project 2011 Email: [email protected] Website : www.sphereproject.org The Sphere Project was initiated in 1997 by a group of NGOs and the Red Cross and Red Crescent Movement to develop a set of universal minimum standards in core areas of humanitarian response: the Sphere Handbook. -
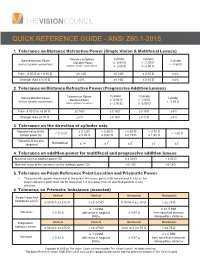
Quick Reference Guide - Ansi Z80.1-2015
QUICK REFERENCE GUIDE - ANSI Z80.1-2015 1. Tolerance on Distance Refractive Power (Single Vision & Multifocal Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -4.50 D (minus cylinder convention) ≤ -2.00 D ≤ -4.50 D From - 6.50 D to + 6.50 D ± 0.13 D ± 0.13 D ± 0.15 D ± 4% Stronger than ± 6.50 D ± 2% ± 0.13 D ± 0.15 D ± 4% 2. Tolerance on Distance Refractive Power (Progressive Addition Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -3.50 D (minus cylinder convention) ≤ -2.00 D ≤ -3.50 D From -8.00 D to +8.00 D ± 0.16 D ± 0.16 D ± 0.18 D ± 5% Stronger than ±8.00 D ± 2% ± 0.16 D ± 0.18 D ± 5% 3. Tolerance on the direction of cylinder axis Nominal value of the ≥ 0.12 D > 0.25 D > 0.50 D > 0.75 D < 0.12 D > 1.50 D cylinder power (D) ≤ 0.25 D ≤ 0.50 D ≤ 0.75 D ≤ 1.50 D Tolerance of the axis Not Defined ° ° ° ° ° (degrees) ± 14 ± 7 ± 5 ± 3 ± 2 4. Tolerance on addition power for multifocal and progressive addition lenses Nominal value of addition power (D) ≤ 4.00 D > 4.00 D Nominal value of the tolerance on the addition power (D) ± 0.12 D ± 0.18 D 5. Tolerance on Prism Reference Point Location and Prismatic Power • The prismatic power measured at the prism reference point shall not exceed 0.33Δ or the prism reference point shall not be more than 1.0 mm away from its specified position in any direction. -

Area, Volume and Surface Area
The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 11 AREA, VOLUME AND SURFACE AREA A guide for teachers - Years 8–10 June 2011 YEARS 810 Area, Volume and Surface Area (Measurement and Geometry: Module 11) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the international Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑NonCommercial‑NoDerivs 3.0 Unported License. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 11 AREA, VOLUME AND SURFACE AREA A guide for teachers - Years 8–10 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge YEARS 810 {4} A guide for teachers AREA, VOLUME AND SURFACE AREA ASSUMED KNOWLEDGE • Knowledge of the areas of rectangles, triangles, circles and composite figures. • The definitions of a parallelogram and a rhombus. • Familiarity with the basic properties of parallel lines. • Familiarity with the volume of a rectangular prism. • Basic knowledge of congruence and similarity. • Since some formulas will be involved, the students will need some experience with substitution and also with the distributive law. -

1 University of California, Berkeley Physics 7A, Section 1, Spring 2009
1 University of California, Berkeley Physics 7A, Section 1, Spring 2009 (Yury Kolomensky) SOLUTIONS TO THE SECOND MIDTERM Maximum score: 100 points 1. (10 points) Blitz (a) hoop, disk, sphere This is a set of simple questions to warm you up. The (b) disk, hoop, sphere problem consists of five questions, 2 points each. (c) sphere, hoop, disk 1. Circle correct answer. Imagine a basketball bouncing on a court. After a dozen or so (d) sphere, disk, hoop bounces, the ball stops. From this, you can con- (e) hoop, sphere, disk clude that Answer: (d). The object with highest moment of (a) Energy is not conserved. inertia has the largest kinetic energy at the bot- (b) Mechanical energy is conserved, but only tom, and would reach highest elevation. The ob- for a single bounce. ject with the smallest moment of inertia (sphere) (c) Total energy in conserved, but mechanical will therefore reach lowest altitude, and the ob- energy is transformed into other types of ject with the largest moment of inertia (hoop) energy (e.g. heat). will be highest. (d) Potential energy is transformed into kinetic 4. A particle attached to the end of a massless rod energy of length R is rotating counter-clockwise in the (e) None of the above. horizontal plane with a constant angular velocity ω as shown in the picture below. Answer: (c) 2. Circle correct answer. In an elastic collision ω (a) momentum is not conserved but kinetic en- ergy is conserved; (b) momentum is conserved but kinetic energy R is not conserved; (c) both momentum and kinetic energy are conserved; (d) neither kinetic energy nor momentum is Which direction does the vector ~ω point ? conserved; (e) none of the above. -

Riemann Surfaces
RIEMANN SURFACES AARON LANDESMAN CONTENTS 1. Introduction 2 2. Maps of Riemann Surfaces 4 2.1. Defining the maps 4 2.2. The multiplicity of a map 4 2.3. Ramification Loci of maps 6 2.4. Applications 6 3. Properness 9 3.1. Definition of properness 9 3.2. Basic properties of proper morphisms 9 3.3. Constancy of degree of a map 10 4. Examples of Proper Maps of Riemann Surfaces 13 5. Riemann-Hurwitz 15 5.1. Statement of Riemann-Hurwitz 15 5.2. Applications 15 6. Automorphisms of Riemann Surfaces of genus ≥ 2 18 6.1. Statement of the bound 18 6.2. Proving the bound 18 6.3. We rule out g(Y) > 1 20 6.4. We rule out g(Y) = 1 20 6.5. We rule out g(Y) = 0, n ≥ 5 20 6.6. We rule out g(Y) = 0, n = 4 20 6.7. We rule out g(C0) = 0, n = 3 20 6.8. 21 7. Automorphisms in low genus 0 and 1 22 7.1. Genus 0 22 7.2. Genus 1 22 7.3. Example in Genus 3 23 Appendix A. Proof of Riemann Hurwitz 25 Appendix B. Quotients of Riemann surfaces by automorphisms 29 References 31 1 2 AARON LANDESMAN 1. INTRODUCTION In this course, we’ll discuss the theory of Riemann surfaces. Rie- mann surfaces are a beautiful breeding ground for ideas from many areas of math. In this way they connect seemingly disjoint fields, and also allow one to use tools from different areas of math to study them. -

Tight Immersions of Simplicial Surfaces in Three Space
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Pergamon Topology Vol. 35, No. 4, pp. 863-873, 19% Copyright Q 1996 Elsevier Sctence Ltd Printed in Great Britain. All tights reserved CO4&9383/96 $15.00 + 0.00 0040-9383(95)00047-X TIGHT IMMERSIONS OF SIMPLICIAL SURFACES IN THREE SPACE DAVIDE P. CERVONE (Received for publication 13 July 1995) 1. INTRODUCTION IN 1960,Kuiper [12,13] initiated the study of tight immersions of surfaces in three space, and showed that every compact surface admits a tight immersion except for the Klein bottle, the real projective plane, and possibly the real projective plane with one handle. The fate of the latter surface went unresolved for 30 years until Haab recently proved [9] that there is no smooth tight immersion of the projective plane with one handle. In light of this, a recently described simplicial tight immersion of this surface [6] came as quite a surprise, and its discovery completes Kuiper’s initial survey. Pinkall [17] broadened the question in 1985 by looking for tight immersions in each equivalence class of immersed surfaces under image homotopy. He first produced a complete description of these classes, and proceeded to generate tight examples in all but finitely many of them. In this paper, we improve Pinkall’s result by giving tight simplicial examples in all but two of the immersion classes under image homotopy for which tight immersions are possible, and in particular, we point out and resolve an error in one of his examples that would have left an infinite number of immersion classes with no tight examples. -

The Geometry of the Disk Complex
JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY Volume 26, Number 1, January 2013, Pages 1–62 S 0894-0347(2012)00742-5 Article electronically published on August 22, 2012 THE GEOMETRY OF THE DISK COMPLEX HOWARD MASUR AND SAUL SCHLEIMER Contents 1. Introduction 1 2. Background on complexes 3 3. Background on coarse geometry 6 4. Natural maps 8 5. Holes in general and the lower bound on distance 11 6. Holes for the non-orientable surface 13 7. Holes for the arc complex 14 8. Background on three-manifolds 14 9. Holes for the disk complex 18 10. Holes for the disk complex – annuli 19 11. Holes for the disk complex – compressible 22 12. Holes for the disk complex – incompressible 25 13. Axioms for combinatorial complexes 30 14. Partition and the upper bound on distance 32 15. Background on Teichm¨uller space 41 16. Paths for the non-orientable surface 44 17. Paths for the arc complex 47 18. Background on train tracks 48 19. Paths for the disk complex 50 20. Hyperbolicity 53 21. Coarsely computing Hempel distance 57 Acknowledgments 60 References 60 1. Introduction Suppose M is a compact, connected, orientable, irreducible three-manifold. Sup- pose S is a compact, connected subsurface of ∂M so that no component of ∂S bounds a disk in M. In this paper we study the intrinsic geometry of the disk complex D(M,S). The disk complex has a natural simplicial inclusion into the curve complex C(S). Surprisingly, this inclusion is generally not a quasi-isometric embedding; there are disks which are close in the curve complex yet far apart in the disk complex.