DOCSLIB.ORG

The Cosmic Web! What Does Our Universe Look Like on the Largest Scale?

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Cosmic Web! What Does Our Universe Look Like on the Largest Scale? Lecture III The Cosmic Web! what does our Universe look like on the largest scale? aurorasimionescu.wordpress.com/teaching “Large-scale structure” refers to spatial scales larger than single galaxies: superclusters, clusters, groups, filaments, walls, voids What structure is our own Galaxy embedded in? The Local Group What structure is our own Galaxy embedded in? The Virgo Supercluster: a ~ 60 Mpc flattened structure, centered on the Virgo Cluster; the Local Group is at the outskirts. We are falling towards Virgo with ~ 300 km/s, and will get there in about 10 - 15 Gyr What structure is our own Galaxy embedded in? The Laniakea Supercluster find locations where peculiar velocity flows diverge, rather than defining structures based on galaxy number overdensity R. Brent Tully et al. Nature 513, 71 (2014) Redshift surveys To map and quantify the LSS (and compare with theoretical predictions), we need redshift surveys: mapping the 3-D distribution of galaxies in space (2D position on the sky plus redshift used as distance indicator) The 2dF (2 degree Field) redshift survey done with the 3.9-m Anglo-Australian telescope from 1997-2002 – Redshifts of ~ 250,000 galaxies with B < 19.5 mag, covering 5% of the sky reaching to z ~ 0.3 The Sloan Digital Sky Survey (SDSS) done with a dedicated 2.5-m telescope at Apache Point Observatory in New Mexico – Multicolor imaging to r ~ 23 mag, and spectra of galaxies down to r < 17.5 mag, reaching to z ~ 0.7; final data release covers 35% of sky and spectra from 3 million objects The 2dF Galaxy Redshift Survey How do we quantify Large-Scale Structure? If galaxies are clustered, they are “correlated”. This is usually quantified using the (c+v)T0 p1+β 2-pointλ0 =correlation function= λ, ξ0, defined as an “excess probability” of finding p1 v2/c2 p1 β another galaxy− at a distance− r from some galaxy, relative to a uniform random p1+β distributionλ0 =(1+.z)λ0 = p1 β λ0 − Letn ¯ be the average number density of galaxies. The probability of finding a galaxy in the volume element dV is: P1 =¯ndV The probability of finding a galaxy in the volume element dV at location x and another galaxy at location y is: 2 P2 =(¯ndV ) [1 + ⇠(x, y)] 2 If the galaxies are uncorrelated, P2 =(P1) and ⇠ = 0. For a statistically homogeneous and isotropic universe, ⇠ can only depend on r = x y . | − | 1 (c+v)T0 p1+β λ0 = = λ0 p1 v2/c2 p1 β − − p1+β λ0 =(1+z)λ0 = p1 β λ0 − Letn ¯ be the average number density of galaxies. The probability of finding a galaxy in the volume element dV is: P1 =¯ndV The probability of finding a galaxy in the volume element dV at location x and another galaxy at location y is: 2 P2 =(¯ndV ) [1 + ⇠(x, y)] 2 If the galaxiesCorrelation are function uncorrelated, measured by 2dFP2 =(P1) and ⇠ = 0. For a statistically homogeneousRoughly a power-law and isotropic universe, ⇠ can only depend on r = x y . γ | − | ⇠(r)= r − r0 For galaxies⇣ of⌘ average brightness, r0~5Mpc and γ~1.7 ! Βrighter galaxies are clustered more strongly than fainter ones; redder galaxies are clustered more strongly than bluer ones (this is related to galaxy evolution!) E. Hawkins et al. 2003, MNRAS 346,78 1 (c+v)T0 p1+β λ0 = = λ0 p1 v2/c2 p1 β − − p1+β λ0 =(1+z)λ0 = p1 β λ0 − Letn ¯ be the average number density of galaxies. The probability of finding a galaxy in the volume element dV is: P1 =¯ndV The probability of finding a galaxy in the volume element dV at location x and another galaxy at location y is: How do we quantify Large-Scale Structure? 2 An alternative description of the statistical properties of a randomP2 field=(¯ isndV the ) [1 + ⇠(x, y)] Fourier power spectrum, P(k). The larger P(k), the larger the amplitude of fluctuations on length scale L=2π/k. 2 ! If the galaxies are uncorrelated, P2 =(P1) and ⇠ = 0. For a statistically The density fluctuations homogeneousare decomposed into and a sum isotropic of plane waves universe, of the form⇠ can only depend on r = x y . δ(x)=⌃a cos(x k) | − | k · P(k) describes the mean of the squares |ak|2 of the amplitudes, averaged over all |k|=k. γ P(k) and the correlation function⇠(r are)= relatedr through− a Fourier transform. r0 ⇣ ⌘ 2dF measurement of P(k) W.J. Percival et al., MNRAS 337, 1068 (2002) Of course P(k) and ξ (r) depend on cosmic time! 1 Challenges in quantifying Large-Scale Structure via power spectra and correlation functions, I Very different images can have the same power spectrum! ! Knowing only the power spectrum is sufficient to fully describe a random field ONLY in the special case of a Gaussian random field ! (δ(x) is Gaussian) ! The phase space information (ensemble of peculiar velocities) is important, in addition to the spatial distribution. Challenges in quantifying Large-Scale Structure via power spectra and correlation functions, II • brighter galaxies are clustered more strongly than fainter ones; redder galaxies are clustered more strongly than bluer ones • density fluctuations in mass and in light are not necessarily the same! (so-called “galaxy biasing”) Smaller fluctuations ride atop of the larger density waves, which lift them up in bunches; thus the highest peaks (densest fluctuations) are clustered more strongly than the average ones. This bias gets stronger at higher redshifts! Le Fevre et al. Large-scale structure formation and evolution Structure Formation and Evolution! From this (Δρ/ρ ~ 10 -6)! to this ! (Δρ/ρ ~ 10 +2)! to this! (Δρ/ρ ~ 10 +6)! (c+v)T0 p1+β λ0 = = λ0 p1 v2/c2 p1 β − − p1+β λ0 =(1+z)λ0 = p1 β λ0 − Letn ¯ be the average number density of galaxies. The probability of finding a galaxy in the volume element dV is: P1 =¯ndV The probability of finding a galaxy in the volume element dV at location x and another galaxy at location y is: (c+v)T0 p1+β λ0 = = λ0 p1 v2/c2 p1 β − − 2 P2 p=(¯1+β ndV ) [1 + ⇠(x, y)] λ0 =(1+z)λ0 = p1 β λ0 − 2 If the galaxies are uncorrelated, P2 =(P1) and ⇠ = 0. For a statistically homogeneous and isotropicLetn ¯ be the universe, average number⇠ can density only of galaxies. depend The on probabilityr = x of findingy . a galaxy in the volume element dV is: | − | δ(x)=⌃akcos(x k) · P1 =¯ndV (c+v)T0 p1+β λ0 = = λ0 p1 v2/c2 p1 β − − p1+β The probability of finding a galaxy in the volume element dV at location x and λ0 =(1+z)λ0 = p1 β λ0 − another galaxy2 6 at location y is: ↵ 32⇡Z e neni 2⇡ h⌫/kB T ✏⌫ = 2 e− gff(T,⌫) Letn ¯ be the average number density3m of galaxies.c3 The probabilityP32 k=(¯ndVTm of finding) [1 + ⇠(x, y)] a galaxy in the volume element dV is: e r B e 2 If the galaxies are uncorrelated, P2 =(P1) and ⇠ = 0. For a statistically ↵ P1 =¯ndV ✏⌫ is flat for h⌫homogeneous<< kBT andand isotropic exponentially universe, ⇠ can only decreasing depend on r for= xh⌫y >k. BT . ∆TheTSZ probability of finding a galaxy in the volume element dV at location x and | − | = f(⌫)y δ(x)=⌃akcos(x k) TCMBanother galaxy at locationc y is: · γ 2 r − P2 =(¯ndV ) [1 + ⇠(x, y)] 2 6 ⇠(r)= 32⇡Z e neni 2⇡ r0 2↵ h⌫/kB T If the galaxies are uncorrelated, P2 =(P1✏)⌫ and= ⇠ = 0. For3 a statistically e− gff(T,⌫) homogeneous and isotropic universe, ⇠ can only depend3 onmerc= x y .3kBTme ⇣ ⌘ | −r| δ(x)=⌃akcos(x k) ↵ · ✏⌫ is flat for h⌫ << kBT and exponentially decreasing for h⌫ >kBT . ∆TSZ = f(⌫)y TCMB c 2 6 ↵ 32⇡Z e neni 2⇡ γ h⌫/k T @⇢ ✏ = r −e− B g (T,⌫) Equations⌫ of3 mmotionc⇠3(r)= of3 kuniformTm expandingff universe @t + (⇢v)=0 e r Br0 e r↵· @v ✏⌫ is flat for h⌫ << kBT andP exponentially⇣ ⌘ decreasing for h⌫ >kBT . +(v∆TSZ = )f(v⌫)y= r Φ @t TCMB toc account ⇢for expansion with time, it is useful to γ · r r − −transformr to comoving coordinates 2 ⇠(r)= @⇢ Φ =4⇡Gr0⇢ ⇤ +r=a(t)x;( ⇢v=vd)=0r/dt=(ȧ/a)r+u! ⇣ ⌘ @t r · r − Hubble’s@v +( law:v v=) vHr=, thus H=P ȧ/a andΦ ! u is the peculiar@t velocity expressed inr ⇢comoving coordinates 2 · r − r @⇢ a(t)Φ is=4 called⇡G the⇢ “scale⇤ factor" @t + (⇢v)=0 @v r · P r − +(v )v = r Φ 2 Now, @considert · rthe evolution− ⇢ r of a spherical volume of radius L(t)=Ld 0a(t)L (if we chooseGM small L 2Φ =4⇡G⇢ ⇤ thenr GR corrections− become small and we can use Newtonian dynamics).2 =d 2ExpansionL 2GM will slow down because of gravitational pull of matter insidedt sphere: L −2 = 2 d2L GM 3 dt − L = 3 2 2 L L u u dt − L V =4⇡ ⇢ = ⇢ + L3 V =4u⇡ ⇢ = ⇢m +m 2 V =4⇡ ⇢ = ⇢ + 3 2 c 3 m c2 3 c 4⇡G⇢m with respect to a pointa¨ =in time where3 a we know the density to be ρ0 4⇡G⇢m ⇢ (t−)=⇢ a3/a(t)3 a¨ = 3 a m 0 0 − so,3 in a matter3 dominated Universe, we obtain ⇢m(t)=⇢0a0/a(t) 4⇡G⇢ a3 (deceleration must be non-zero! 0 0 1 Here is where Einstein added his cosmological a¨ = 2 3 a constant term at first to force ä to be 0) − 3 3 2 4⇡G⇢0a0 2˙a 8⇡G⇢0a0 2˙aa¨ = d(˙a )/dt = 3 a2 = 3 d( 1/a)/dt 3 − − − 2 8⇡G⇢0a0 1 2 1 a˙ = 3 a kc − 1 1 (c+v)T0 p1+β λ0 = = λ0 p1 v2/c2 p1 β − − p1+β λ0 =(1+z)λ0 = p1 β λ0 − Letn ¯ be the average number density of galaxies.
Load more

Recommended publications
  • Highlights and Discoveries from the Chandra X-Ray Observatory1
    Highlights and Discoveries from the Chandra X-ray Observatory1 H Tananbaum1, M C Weisskopf2, W Tucker1, B Wilkes1 and P Edmonds1 1Smithsonian Astrophysical Observatory, 60 Garden Street, Cambridge, MA 02138. 2 NASA/Marshall Space Flight Center, ZP12, 320 Sparkman Drive, Huntsville, AL 35805. Abstract. Within 40 years of the detection of the first extrasolar X-ray source in 1962, NASA’s Chandra X-ray Observatory has achieved an increase in sensitivity of 10 orders of magnitude, comparable to the gain in going from naked-eye observations to the most powerful optical telescopes over the past 400 years. Chandra is unique in its capabilities for producing sub-arcsecond X-ray images with 100-200 eV energy resolution for energies in the range 0.08<E<10 keV, locating X-ray sources to high precision, detecting extremely faint sources, and obtaining high resolution spectra of selected cosmic phenomena. The extended Chandra mission provides a long observing baseline with stable and well-calibrated instruments, enabling temporal studies over time-scales from milliseconds to years. In this report we present a selection of highlights that illustrate how observations using Chandra, sometimes alone, but often in conjunction with other telescopes, have deepened, and in some instances revolutionized, our understanding of topics as diverse as protoplanetary nebulae; massive stars; supernova explosions; pulsar wind nebulae; the superfluid interior of neutron stars; accretion flows around black holes; the growth of supermassive black holes and their role in the regulation of star formation and growth of galaxies; impacts of collisions, mergers, and feedback on growth and evolution of groups and clusters of galaxies; and properties of dark matter and dark energy.
    [Show full text]
  • Stsci Newsletter: 2011 Volume 028 Issue 02
    National Aeronautics and Space Administration Interacting Galaxies UGC 1810 and UGC 1813 Credit: NASA, ESA, and the Hubble Heritage Team (STScI/AURA) 2011 VOL 28 ISSUE 02 NEWSLETTER Space Telescope Science Institute We received a total of 1,007 proposals, after accounting for duplications Hubble Cycle 19 and withdrawals. Review process Proposal Selection Members of the international astronomical community review Hubble propos- als. Grouped in panels organized by science category, each panel has one or more “mirror” panels to enable transfer of proposals in order to avoid conflicts. In Cycle 19, the panels were divided into the categories of Planets, Stars, Stellar Rachel Somerville, [email protected], Claus Leitherer, [email protected], & Brett Populations and Interstellar Medium (ISM), Galaxies, Active Galactic Nuclei and Blacker, [email protected] the Inter-Galactic Medium (AGN/IGM), and Cosmology, for a total of 14 panels. One of these panels reviewed Regular Guest Observer, Archival, Theory, and Chronology SNAP proposals. The panel chairs also serve as members of the Time Allocation Committee hen the Cycle 19 Call for Proposals was released in December 2010, (TAC), which reviews Large and Archival Legacy proposals. In addition, there Hubble had already seen a full cycle of operation with the newly are three at-large TAC members, whose broad expertise allows them to review installed and repaired instruments calibrated and characterized. W proposals as needed, and to advise panels if the panelists feel they do not have The Advanced Camera for Surveys (ACS), Cosmic Origins Spectrograph (COS), the expertise to review a certain proposal. Fine Guidance Sensor (FGS), Space Telescope Imaging Spectrograph (STIS), and The process of selecting the panelists begins with the selection of the TAC Chair, Wide Field Camera 3 (WFC3) were all close to nominal operation and were avail- about six months prior to the proposal deadline.
    [Show full text]
  • Astrophysics in 2006 3
    ASTROPHYSICS IN 2006 Virginia Trimble1, Markus J. Aschwanden2, and Carl J. Hansen3 1 Department of Physics and Astronomy, University of California, Irvine, CA 92697-4575, Las Cumbres Observatory, Santa Barbara, CA: ([email protected]) 2 Lockheed Martin Advanced Technology Center, Solar and Astrophysics Laboratory, Organization ADBS, Building 252, 3251 Hanover Street, Palo Alto, CA 94304: ([email protected]) 3 JILA, Department of Astrophysical and Planetary Sciences, University of Colorado, Boulder CO 80309: ([email protected]) Received ... : accepted ... Abstract. The fastest pulsar and the slowest nova; the oldest galaxies and the youngest stars; the weirdest life forms and the commonest dwarfs; the highest energy particles and the lowest energy photons. These were some of the extremes of Astrophysics 2006. We attempt also to bring you updates on things of which there is currently only one (habitable planets, the Sun, and the universe) and others of which there are always many, like meteors and molecules, black holes and binaries. Keywords: cosmology: general, galaxies: general, ISM: general, stars: general, Sun: gen- eral, planets and satellites: general, astrobiology CONTENTS 1. Introduction 6 1.1 Up 6 1.2 Down 9 1.3 Around 10 2. Solar Physics 12 2.1 The solar interior 12 2.1.1 From neutrinos to neutralinos 12 2.1.2 Global helioseismology 12 2.1.3 Local helioseismology 12 2.1.4 Tachocline structure 13 arXiv:0705.1730v1 [astro-ph] 11 May 2007 2.1.5 Dynamo models 14 2.2 Photosphere 15 2.2.1 Solar radius and rotation 15 2.2.2 Distribution of magnetic fields 15 2.2.3 Magnetic flux emergence rate 15 2.2.4 Photospheric motion of magnetic fields 16 2.2.5 Faculae production 16 2.2.6 The photospheric boundary of magnetic fields 17 2.2.7 Flare prediction from photospheric fields 17 c 2008 Springer Science + Business Media.
    [Show full text]
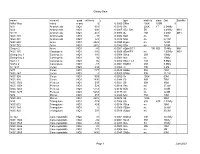
  • Galaxy Data Name Constell
    Galaxy Data name constell. quadvel km/s z type width ly starsDist. Satellite Milky Way many many 0 0.0000 SBbc 106K 200M 0 M31 Andromeda NQ1 -301 -0.0010 SA 220K 1T 2.54Mly M32 Andromeda NQ1 -200 -0.0007 cE2 Sat. 5K 2.49Mly M31 M110 Andromeda NQ1 -241 -0.0008 dE 15K 2.69M M31 NGC 404 Andromeda NQ1 -48 -0.0002 SA0 no 10M NGC 891 Andromeda NQ1 528 0.0018 SAb no 27.3M NGC 680 Aries NQ1 2928 0.0098 E pec no 123M NGC 772 Aries NQ1 2472 0.0082 SAb no 130M Segue 2 Aries NQ1 -40 -0.0001 dSph/GC?. 100 5E5 114Kly MW NGC 185 Cassiopeia NQ1 -185 -0.0006dSph/E3 no 2.05Mly M31 Dwingeloo 1 Cassiopeia NQ1 110 0.0004 SBcd 25K 10Mly Dwingeloo 2 Cassiopeia NQ1 94 0.0003Iam no 10Mly Maffei 1 Cassiopeia NQ1 66 0.0002 S0pec E3 75K 9.8Mly Maffei 2 Cassiopeia NQ1 -17 -0.0001 SABbc 25K 9.8Mly IC 1613 Cetus NQ1 -234 -0.0008Irr 10K 2.4M M77 Cetus NQ1 1177 0.0039 SABd 95K 40M NGC 247 Cetus NQ1 0 0.0000SABd 50K 11.1M NGC 908 Cetus NQ1 1509 0.0050Sc 105K 60M NGC 936 Cetus NQ1 1430 0.0048S0 90K 75M NGC 1023 Perseus NQ1 637 0.0021 S0 90K 36M NGC 1058 Perseus NQ1 529 0.0018 SAc no 27.4M NGC 1263 Perseus NQ1 5753 0.0192SB0 no 250M NGC 1275 Perseus NQ1 5264 0.0175cD no 222M M74 Pisces NQ1 857 0.0029 SAc 75K 30M NGC 488 Pisces NQ1 2272 0.0076Sb 145K 95M M33 Triangulum NQ1 -179 -0.0006 SA 60K 40B 2.73Mly NGC 672 Triangulum NQ1 429 0.0014 SBcd no 16M NGC 784 Triangulum NQ1 0 0.0000 SBdm no 26.6M NGC 925 Triangulum NQ1 553 0.0018 SBdm no 30.3M IC 342 Camelopardalis NQ2 31 0.0001 SABcd 50K 10.7Mly NGC 1560 Camelopardalis NQ2 -36 -0.0001Sacd 35K 10Mly NGC 1569 Camelopardalis NQ2 -104 -0.0003Ibm 5K 11Mly NGC 2366 Camelopardalis NQ2 80 0.0003Ibm 30K 10M NGC 2403 Camelopardalis NQ2 131 0.0004Ibm no 8M NGC 2655 Camelopardalis NQ2 1400 0.0047 SABa no 63M Page 1 2/28/2020 Galaxy Data name constell.
    [Show full text]
  • Arxiv:1007.2659V1 [Astro-Ph.SR] 15 Jul 2010 Aeteesasecletcrnmtr N Edsrb Why Describe Stars
    The Astronomy & Astrophysics Review manuscript No. (will be inserted by the editor) Evolutionary and pulsational properties of white dwarf stars Leandro G. Althaus Alejandro H. Corsico´ Jordi Isern Enrique Garc´ıa–Berro· · · Received: October 22, 2018/ Accepted: October 22, 2018 Abstract White dwarf stars are the final evolutionary stage of the vast majority of stars, including our Sun. Since the coolest white dwarfs are very old objects, the present popula- tion of white dwarfs contains a wealth of information on the evolution of stars from birth to death, and on the star formation rate throughout the history of our Galaxy. Thus, the study of white dwarfs has potential applications to different fields of astrophysics. In partic- ular, white dwarfs can be used as independent reliable cosmic clocks, and can also provide valuable information about the fundamental parameters of a wide variety of stellar popu- lations, like our Galaxy and open and globular clusters. In addition, the high densities and temperatures characterizing white dwarfs allow to use these stars as cosmic laboratories for studying physical processes under extreme conditions that cannot be achieved in terrestrial laboratories. Last but not least, since many white dwarf stars undergo pulsational instabili- ties, the study of their properties constitutes a powerful tool for applications beyond stellar astrophysics. In particular, white dwarfs can be used to constrain fundamental properties of elementary particles such as axions and neutrinos, and to study problems related to the variation of fundamental constants. These potential applications of white dwarfs have led to a renewed interest in the cal- culation of very detailed evolutionary and pulsational models for these stars.
    [Show full text]
  • MARGARET J. GELLER Education: University of California, Berkeley, BA
    MARGARET J. GELLER Education: University of California, Berkeley, B.A. (physics, 1970) Princeton University, M.A. (physics, 1972) Princeton University, Ph.D. (physics, 1974) Positions: 1970-1973 NSF Predoctoral Fellow, Princeton University 1974-1976 Center Postdoctoral Fellow, Center for Astrophysics 1976-1978 Research Fellow, Harvard College Observatory 1977-1980 Lecturer, Harvard University 1978-1980 Research Associate, Harvard College Observatory 1978-1980 Senior Visiting Fellow, Institute of Astronomy, Cambridge University 1980-1983 Assistant Professor, Harvard University 1983-1991 Astronomer, Smithsonian Astrophysical Observatory 1991- Senior Scientist, Smithsonian Astrophysical Observatory Professional Societies: International Astronomical Union American Association for the Advancement of Science (Fellow 1992) American Physical Society (Fellow 1995) Honorary Societies: Phi Beta Kappa (elected 1969) American Academy of Arts and Sciences (elected 1990) National Academy of Sciences (elected 1992) Honorary Degrees: D.S.H.C. Connecticut College (1995) D.S.H.C. Gustavus Adolphus College (1997) D.S.H.C. University of Massachusetts, Dartmouth (2000) D.S.H.C. Colby College (2009) D.S.H.C. Universitat Rovira i Virgili (Tarragona, Spain) (2009) D.S.H.C. Dartmouth College (2014) L.H.C. University of Turin (2017) Awards (Selected) : MacArthur Fellowship (1990-1995) AAAS Newcomb - Cleveland Prize (1989) Best Case Study (for redshift survey graphics), IEEE SIGGRAPH Visualization (1992) Helen Sawyer Hogg Lectureship, Royal Astronomical Society
    [Show full text]
  • The Dark Matter Distribution in Abell 383: Evidence for a Shallow
    Accepted to ApJL A Preprint typeset using LTEX style emulateapj v. 11/10/09 THE DARK MATTER DISTRIBUTION IN ABELL 383: EVIDENCE FOR A SHALLOW DENSITY CUSP FROM IMPROVED LENSING, STELLAR KINEMATIC AND X-RAY DATA Andrew B. Newman1, Tommaso Treu2, Richard S. Ellis1, David J. Sand2,3 Accepted to ApJL ABSTRACT We extend our analyses of the dark matter (DM) distribution in relaxed clusters to the case of Abell 383, a luminous X-ray cluster at z=0.189 with a dominant central galaxy and numerous strongly-lensed features. Following our earlier papers, we combine strong and weak lensing constraints secured with Hubble Space Telescope and Subaru imaging with the radial profile of the stellar velocity dispersion of the central galaxy, essential for separating the baryonic mass distribution in the cluster core. Hydrostatic mass estimates from Chandra X-ray observations further constrain the solution. These combined datasets provide nearly continuous constraints extending from 2 kpc to 1.5 Mpc in radius, allowing stringent tests of results from recent numerical simulations. Two key improvements in our data and its analysis make this the most robust case yet for a shallow slope β of the DM density −β profile ρDM ∝ r on small scales. First, following deep Keck spectroscopy, we have secured the stellar velocity dispersion profile to a radius of 26 kpc for the first time in a lensing cluster. Secondly, we improve our previous analysis by adopting a triaxial DM distribution and axisymmetric dynamical models. We demonstate that in this remarkably well-constrained system, the logarithmic slope of the DM density at small radii is β < 1.0 (95% confidence).
    [Show full text]
  • The Universe Contents 3 HD 149026 B
    History . 64 Antarctica . 136 Utopia Planitia . 209 Umbriel . 286 Comets . 338 In Popular Culture . 66 Great Barrier Reef . 138 Vastitas Borealis . 210 Oberon . 287 Borrelly . 340 The Amazon Rainforest . 140 Titania . 288 C/1861 G1 Thatcher . 341 Universe Mercury . 68 Ngorongoro Conservation Jupiter . 212 Shepherd Moons . 289 Churyamov- Orientation . 72 Area . 142 Orientation . 216 Gerasimenko . 342 Contents Magnetosphere . 73 Great Wall of China . 144 Atmosphere . .217 Neptune . 290 Hale-Bopp . 343 History . 74 History . 218 Orientation . 294 y Halle . 344 BepiColombo Mission . 76 The Moon . 146 Great Red Spot . 222 Magnetosphere . 295 Hartley 2 . 345 In Popular Culture . 77 Orientation . 150 Ring System . 224 History . 296 ONIS . 346 Caloris Planitia . 79 History . 152 Surface . 225 In Popular Culture . 299 ’Oumuamua . 347 In Popular Culture . 156 Shoemaker-Levy 9 . 348 Foreword . 6 Pantheon Fossae . 80 Clouds . 226 Surface/Atmosphere 301 Raditladi Basin . 81 Apollo 11 . 158 Oceans . 227 s Ring . 302 Swift-Tuttle . 349 Orbital Gateway . 160 Tempel 1 . 350 Introduction to the Rachmaninoff Crater . 82 Magnetosphere . 228 Proteus . 303 Universe . 8 Caloris Montes . 83 Lunar Eclipses . .161 Juno Mission . 230 Triton . 304 Tempel-Tuttle . 351 Scale of the Universe . 10 Sea of Tranquility . 163 Io . 232 Nereid . 306 Wild 2 . 352 Modern Observing Venus . 84 South Pole-Aitken Europa . 234 Other Moons . 308 Crater . 164 Methods . .12 Orientation . 88 Ganymede . 236 Oort Cloud . 353 Copernicus Crater . 165 Today’s Telescopes . 14. Atmosphere . 90 Callisto . 238 Non-Planetary Solar System Montes Apenninus . 166 How to Use This Book 16 History . 91 Objects . 310 Exoplanets . 354 Oceanus Procellarum .167 Naming Conventions . 18 In Popular Culture .
    [Show full text]
  • Annual Report 2011
    ANNUAL REPORT 2011 ON THE COVER: HEADQUARTERS LOCATION: FY2011 Ace summit operations team Kamuela, Hawai’i, USA Number of Full Time members, from left: Arnold Employees: 115 Matsuda, John Baldwin and MANAGEMENT: Mike Dahler, focus their California Association for Number of Observing attention to removing a Research in Astronomy Astronomers FY2011: 464 single segment from the PARTNER INSTITUTIONS: Number of Keck Science Keck Telescope primary California Institute of Investigations: 400 mirror in the first major step Technology (CIT/Caltech), in the segment recoating Number of Refereed Articles process. University of California (UC), FY2011: 278 National Aeronautics and Fiscal Year begins October 1 BELOW: Space Administration (NASA) The newly commissioned Federal Identification Keck I Laser penetrates the OBSERVATORY DIRECTOR: Number: 95-3972799 night sky from the majestic Taft E. Armandroff landscape of Mauna Kea. DEPUTY DIRECTOR: The laser is part of Keck’s Hilton A. Lewis world leading adaptive optics systems, a technology used to remove the effects of turbulence in Earth’s atmosphere and provides unprecedented image clarity of cosmic targets near and distant. VISION A world in which all humankind is inspired and united by the pursuit of knowledge of the infinite CONTENTS variety and richness of the Universe. Director’s Report . 3 Cosmic Visionaries . 6 Science Highlights . 8 MISSION Finances . 16 To advance the frontiers of astronomy and share Philanthropic Support . .18 our discoveries, inspiring the imagination of all. Reflections . .20 Education & Outreach . .22 Observatory Groundbreaking: 1985 Honors & Recognition . .26 First light Keck I telescope: 1992 Science Bibliography . 28 First light Keck II telescope: 1996 DIRECTOR’s REPORT Taft E.
    [Show full text]
  • A Weak-Lensing Analysis of the Abell 383 Cluster ⋆
    A&A 529, A93 (2011) Astronomy DOI: 10.1051/0004-6361/201015955 & c ESO 2011 Astrophysics A weak-lensing analysis of the Abell 383 cluster Z. Huang1,3,M.Radovich2,A.Grado1, E. Puddu1,A.Romano3,L.Limatola1, and L. Fu4,1 1 INAF Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italy e-mail: [email protected] 2 INAF – Osservatorio Astronomico di Padova, vicolo dell’Osservatorio 5, 35122 Padova, Italy e-mail: [email protected] 3 INAF – Osservatorio Astronomico di Roma, Monte Porzio, 00185 Roma, Italy 4 Key Lab for Astrophysics, Shanghai Normal University, 100 Guilin Road, 200234 Shanghai, PR China Received 20 October 2010 / Accepted 9 February 2011 ABSTRACT Aims. We use deep CFHT and SUBARU uBVRIz archival images of the Abell 383 cluster (z = 0.187) to estimate its mass by weak- lensing. Methods. To this end, we first use simulated images to check the accuracy provided by our Kaiser-Squires-Broadhurst (KSB) pipeline. These simulations include shear testing programme (STEP) 1 and 2 simulations, as well as more realistic simulations of the distortion of galaxy shapes by a cluster with a Navarro-Frenk-White (NFW) profile. From these simulations we estimate the effect of noise on shear measurement and derive the correction terms. The R-band image is used to derive the mass by fitting the observed tangential shear profile with an NFW mass profile. Photometric redshifts are computed from the uBVRIz catalogs. Different methods for the foreground/background galaxy selection are implemented, namely selection by magnitude, color, and photometric redshifts, and the results are compared.
    [Show full text]
  • 2016 Publication Year 2020-04-28T10:16:34Z Acceptance in OA@INAF the Galaxy Cluster Concentration-Mass Scaling Relation Title Gr
    Publication Year 2016 Acceptance in OA@INAF 2020-04-28T10:16:34Z Title The galaxy cluster concentration-mass scaling relation Authors Groener, A. M.; Goldberg, D. M.; Sereno, Mauro DOI 10.1093/mnras/stv2341 Handle http://hdl.handle.net/20.500.12386/24269 Journal MONTHLY NOTICES OF THE ROYAL ASTRONOMICAL SOCIETY Number 455 MNRAS 455, 892–919 (2016) doi:10.1093/mnras/stv2341 The galaxy cluster concentration–mass scaling relation A. M. Groener,1‹ D. M. Goldberg1‹ and M. Sereno2,3 1Department of Physics, Drexel University Philadelphia, PA 19104, USA 2Dipartimento di Fisica e Astronomia, Alma Mater Studiorum Universita` di Bologna, viale Berti Pichat 6/2, I-40127 Bologna, Italy 3INAF, Osservatorio Astronomico di Bologna, via Ranzani 1, I-40127 Bologna, Italy Accepted 2015 October 6. Received 2015 September 18; in original form 2015 July 6 Downloaded from ABSTRACT Scaling relations of clusters have made them particularly important cosmological probes of structure formation. In this work, we present a comprehensive study of the relation between two http://mnras.oxfordjournals.org/ profile observables, concentration (cvir) and mass (Mvir). We have collected the largest known sample of measurements from the literature which make use of one or more of the following reconstruction techniques: weak gravitational lensing (WL), strong gravitational lensing (SL), weak+strong lensing (WL+SL), the caustic method (CM), line-of-sight velocity dispersion (LOSVD), and X-ray. We find that the concentration–mass (c–M) relation is highly variable depending upon the reconstruction technique used. We also find concentrations derived from 14 dark matter-only simulations (at approximately Mvir ∼ 10 M) to be inconsistent with the WL and WL+SL relations at the 1σ level, even after the projection of triaxial haloes is taken at Universitàdi Bologna - Sistema Bibliotecario d'Ateneo on June 1, 2016 into account.
    [Show full text]
  • Dark Matter in Galaxy Clusters: Shape, Projection, and Environment
    Dark Matter in Galaxy Clusters: Shape, Projection, and Environment A Thesis Submitted to the Faculty of Drexel University by Austen M. Groener in partial fulfillment of the requirements for the degree of Doctor of Philosophy September 2015 c Copyright 2015 Austen M. Groener. ii Dedications I dedicate this thesis to my family, and to my wife, who supported me unconditionally throughout my career as a scientist. iii Acknowledgments I have many people to thank for making this work a possibility. Firstly, I would like to thank my advisor, Dr. David Goldberg. His guidance, support, and most of all his patience provided the framework for which I was able to build my work from. I would also like to thank my dissertation committee members, Dr. Michael Vogeley, Dr. Gordon Richards, Dr. Luis Cruz, and Dr. Andrew Hicks, for their constructive criticism and support of my research. I would also like to acknowledge fellow graduate students for their assistance and support. A special thanks to Justin Bird, Markus Rexroth, Frank Jones, Crystal Moorman, and Vishal Kasliwal for allowing me to bounce ideas off of them, which was a truly important but time consuming process. iv Table of Contents List of Tables ........................................... vi List of Figures .......................................... vii Abstract .............................................. ix 1. Introduction .......................................... 1 1.1 The Radial Density Profile.................................. 2 1.2 Cluster Scaling Relations .................................. 5 1.3 Clusters and Environment.................................. 7 1.4 Outline ............................................ 11 2. Cluster Shape and Orientation .............................. 12 2.1 Introduction.......................................... 12 2.2 Triaxial Projections...................................... 14 2.3 Sample and Methods..................................... 15 2.3.1 Simulation Sample .................................... 15 2.3.2 Methods.........................................
    [Show full text]