The SAMI Galaxy Survey: Stellar Population and Structural Trends Across the Fundamental Plane
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Portsmouth Number List 2019
Portsmouth Number List 2019 The RYA Portsmouth Yardstick Scheme is provided to enable clubs to allow boats of different classes to race against each other fairly. The RYA actively encourages clubs to adjust handicaps where classes are either under or over performing compared to the number being used. The Portsmouth Yardstick list combines the Portsmouth numbers with class configuration and the total number of races returned to the RYA in the annual return. This additional data has been provided to help clubs achieve the stated aims of the Portsmouth Yardstick system and make adjustments to Portsmouth Numbers where necessary. Clubs using the PN list should be aware that the list is based on the typical performance of each boat across a variety of clubs and locations. Experimental numbers are based on fewer returns and are to be used as a guide for clubs to allocate as a starting number before reviewing and adjusting where necessary. The list of experimental Portsmouth Numbers will be periodically reviewed by the RYA and is based on data received via PY Online. Users of the PY scheme are reminded that all Portsmouth Numbers published by the RYA should be regarded as a guide only. The RYA list is not definitive and clubs should adjust where necessary. For further information please visit the RYA website: http://www.rya.org.uk/racing/Pages/portsmouthyardstick.aspx RYA PN LIST - Dinghy No. of Change Class Name Rig Spinnaker Number Races Notes Crew from '18 420 2 S C 1111 0 428 2000 2 S A 1112 3 2242 29ER 2 S A 907 -5 277 505 2 S C 903 0 277 -

Southport Yacht Club Sailing @ Southport Yacht Club
SOUTHPORT YACHT CLUB NEWS / INFO Issue Number 29 Summer 2012 / 2013 INFUSION WORLD CHAMPIONSHIPS NACRA AT SYC - HOLLYWELL FESTIVE YC S SEASON 1ST dec - 28TH feb Hardstand Refi t Bays Specialist Workshops Retail Factories Specialist Workshops Main Entrance Southport Yacht Club Gold Members can now save 5% on their boat works. n the heart of the Gold Coast Marine of the partnership between SYC and The BOAT YARD SERVICES Precinct is The Boat Works. Boat Works. All Gold Members can now save Boat Lifting | Shipwrights | Painters As the name suggests, you get The 5% on all service charges relating to haul I out and return to water, barnacle scrapping, Antifouling | Slipway | Engineers Works: there’s nothing that can’t be carried out here. And excellently. waterblasting, hardstand and refit bay charges. The name also suggests the level of The full menu of The Boat Works’s services MARINA & REFIT FACILITIES reassurance boat owners gain from this are listed below. But we should highlight some world-class facility. stand-out advantages: Refi t Bays | Storage Options Stretching over 9.2 hectares of sheltered Our modern facility offers 30 work berths Marina Berths | Hardstand Coomera riverfront, The Boat Works is a full for vessels up to 25m. The covered refit bays take boats up to 24m. service and refit yard, offering businesslike BUSINESS OPPORTUNITIES marine service to pleasure boaters. There are 17,000 square metres of Here you’ll find an enthusiastic crew and hardstand, maintenance and service areas; a Retail Factories | Leasing Opportunities first grade facilities. travelift that can lift up to 70- tonners; plus unique hydraulic trolleys that can lift wider You will also find economical rates courtesy cats, tris, barges and houseboats. -

Buying a Lark Barker, Parker, Rondar, Ovington
Barker, Parker, Rondar, Ovington Buying a Lark Over the 40 years Larks have been in production over 2500 hulls have been made. Some of which are owned and raced regularly, however many are sitting in dinghy parks or garages providing a safe habitat for an abun- dance of wildlife. The materials used and build quality of the Lark means that virtually all of these hulls could be restored with minimum expense and therefore offer an excellent opportunity for sailors on a budget. This means you can buy a Lark second hand from as little as £50, they regularly come up on sites like E-bay, Apollo Duck and in Yachts and Yachting and Dinghy Sailing Magazine as well as on the lark web-site www.larkclass.org . So when shopping for a Lark what should you expect to get for your money: Booking Form Boat Numbers 1-1838 – Baker Lark Boat Numbers 1839-2454 Parker Lark Baker was the original Lark builder from 1967 right Parker took over building the Lark and built a huge num- up until the late 1970’s and built the vast majority of ber of Larks throughout the 1980’s and 1990’s, including Larks in terms of numbers. The boats are still fan- a huge number for Universities and Colleges who often tastic sailing and racing boats, but have suffered replaced theirP fleetsa six boats at a time. Parker Larks from issues with hull andk centreboarder case stiffness are still extremely competitiverke if they have been well as the have agedB (thea oldest are now over 40 years maintained and looked after, andr offer a cheap and old). -

IT's a WINNER! Refl Ecting All That's Great About British Dinghy Sailing
ALeXAnDRA PALACe, LOnDOn 3-4 March 2012 IT'S A WINNER! Refl ecting all that's great about British dinghy sailing 1647 DS Guide (52).indd 1 24/01/2012 11:45 Y&Y AD_20_01-12_PDF.pdf 23/1/12 10:50:21 C M Y CM MY CY CMY K The latest evolution in Sailing Hikepant Technology. Silicon Liquid Seam: strongest, lightest & most flexible seams. D3O Technology: highest performance shock absorption, impact protection solutions. Untitled-12 1 23/01/2012 11:28 CONTENTS SHOW ATTRACTIONS 04 Talks, seminars, plus how to get to the show and where to eat – all you need to make the most out of your visit AN OLYMPICS AT HOME 10 Andy Rice speaks to Stephen ‘Sparky’ Parks about the plus and minus points for Britain's sailing team as they prepare for an Olympic Games on home waters SAIL FOR GOLD 17 How your club can get involved in celebrating the 2012 Olympics SHOW SHOPPING 19 A range of the kit and equipment on display photo: rya* photo: CLubS 23 Whether you are looking for your first club, are moving to another part of the country, or looking for a championship venue, there are plenty to choose WELCOME SHOW MAP enjoy what’s great about British dinghy sailing 26 Floor plans plus an A-Z of exhibitors at the 2012 RYA Volvo Dinghy Show SCHOOLS he RYA Volvo Dinghy Show The show features a host of exhibitors from 29 Places to learn, or improve returns for another year to the the latest hi-tech dinghies for the fast and your skills historical Alexandra Palace furious to the more traditional (and stable!) in London. -

The 49Er Is the Two Person One-Design Skiff Which Has
The Julian Bethwaite designed B14 has been built by Ovington boats since 2001. With the 29er, 49er, Musto Skiff and the 18foot skiff the world class range of skiffs now numbers five. The Boat Ovington's 'secret' in building long lasting epoxy boats is in our ability to apply a polyester gel coat to an epoxy laminate. The hugely popular B14 is a lightweight, 2 person, non-trapeze skiff with blistering performance and a strong international following. The boat enjoys a very large active fleet in the UK. Outstanding power to weight ratio is the key to the B14's blistering performance which is enhanced by a sophisticated rig. A wide range of body weights can remain competitive in all conditions and because of the light loads and easily driven hull form it returns an outstanding performance relative to effort. The Ovington B14 is made from epoxy resins using the unique tried and tested system that successfully makes the fastest Flying Fifteens and International 14s. There changes made to the deck mould to improve ergonomics and pole launching have revolutionised the strength of the hull and made handling the spinnaker easier. Specification Overall Length 6.07 m Waterline Length 4.25 m Beam (sailing) 3.8 m Beam (travelling) 1.66 m Hull Weight 62 kg Mast Height above sheer line 6.25m Main 12 sq.m Jin 5.2 sq.m Asymmetric Spinnaker 29.2 sq.m Designer Julian Bethwaite Boat Options Hull Option 1 Complete boat ready to sail – EX sails. Includes; Fully rigged carbon mast, boom, bow sprit, foils, wings all fittings and ropes. -

Seite 1 Von 3 VELUM Ng
VELUM ng - Wettfahrt Seite 1 von 3 Deutsch- Schweizerischer Motorboot-Club e.V. XXXIX Regatta der Eisernen L31304457 Deutsch- Schweizerischer Motorboot-Club e.V. vorläufige Ergebnisliste 1.Wettfahrt 29. November 2014 Low-Point Wettfahrtleitung: Matthias Hagner & Jörn Thamm Auswertung: Markus Meyer 30.11.2014 - 13:49:07 Gruppe: (1,0) Bahn Lang (Yardstick) 1.Wf / Startzeit: 29.11.2014 12:15:00 PL. NAT SEGELNR BOOTSNAME STEUERMANN/- BOOTSTYP CLUB GES.ZEIT BER.ZEIT FRAU Nila-Ann by 1 GER 100 Team Black Jack CR 950 YCM 00:44:10 00:53:13 Bauen.ch 2 GER 832 Corvus Begher Thomas Longtze YLB 00:47:30 00:55:53 3 SUI 156 Sail North Schroff Daniel Esse 850 SVK 00:49:04 00:57:03 4 SUI 34 Mistral Maier-Ring, Adrian Blu 26 SSCK 00:50:55 00:57:52 5 VIII-3 HOC Neustadt Kaiser, Karlheinz 80er Seefahrtskreuzer YCL 00:54:09 00:58:14 6 AUT 7 seven B Bemetz, Jonas Sun Fast 3200 BSC 00:53:09 00:59:43 7 FRA 820 ToughCookie Eitner Andreas Longtze YCL 00:52:44 01:02:02 8 SUI 46 J Lane Seger, Benu J-88 SVB 00:53:40 01:02:24 9 SUI 160 Carondimonio Smits Sammy Libera B YC Arbon 00:43:46 01:02:31 Hans-Peter 10 GER 450 Jackpot J-70 BYCÜ 00:59:25 01:03:13 Burckhardt 11 GER 3242 Plan/B Lochbrunner Andi B/One LSC 01:00:21 01:03:32 12 Ger 2053 Ralf Breitenfeldt Streamline MYC 00:57:57 01:03:41 van Merkesteyn, 75er Nationaler 13 O 12 Vinga YCL 00:58:46 01:04:35 Roel Kreuzer 14 SUI 33 - Flessati Julian Blu 26 SC Rietli 00:57:52 01:05:45 15 GER 820 Ti Punsh Graf Elmar First Class 8 SCMB 01:03:02 01:06:21 16 AUT 66 Vento Hämmerle Urs Modulo 90 BSC 01:01:48 01:06:27 Speedwave -

The First Fifty Years People, Memories and Reminiscences Contents
McCrae Yacht Club – the First Fifty Years People, Memories and Reminiscences Contents Championships Hosted at McCrae ...................................................................................................2 Our champion sailors...........................................................................................................................5 Classes Sailed over the years.......................................................................................................... 12 Stories from various sailing events.............................................................................................. 25 Rescues and Tall Tales...................................................................................................................... 31 Notable personalities........................................................................................................................ 37 Did you know? – some interesting trivia.................................................................................... 43 Personal Recollections and Reminiscences .............................................................................. 46 The Little America’s Cup – what really happened ….. ............................................................ 53 McCrae Yacht Club History - firsts ................................................................................................ 58 Championships Hosted at McCrae The Club started running championships in the second year of operation. The first championships held in 1963/64 -

Wingflap Octo 05
OCTOBER 2005 Dennis (skipper) and Daniel (crew) Watson, at Jervis Bay in the first heat of the Travellers Trophy, October 2005. Photographer: Mark Watson (dad) p a l f g n i W Countdown to the World Championships Letter from your President And it’s important that we don’t just have a good showing on the sailing side of things, there’re the It’s that time again! Time to dust off the boat and social events! These will culminate in a Harbour get out on the water, if you haven’t already done Cruise on the night of Friday 13th after World’s so. And it’s more exciting than ever this season, Presentation. with the Big Events happening on Sydney Harbour this January. The Poms are coming out in numbers to take us on in our own back yard, so it’s incum- There will be a Toga Party at Woollahra Sailing bent upon us all to put on our best-ever showing! Club on New Year’s Eve. It’s free for members and all B14ers and their guests. We expect some At the last Worlds in Garda, the Aussies came of the Poms will be here at that stage and looking away with 3rd, 4th, 9th, 11th, 13th and 37th. At the for somewhere to party. It will be a laid-back af- previous event in Melbourne, Guy and Rhys Ban- fair, BYO grog and toga. croft achieved the best ever result (so far) for an nd Australian crew with 2 . What can we do this We are currently compiling rosters for volunteers time??? for the event, so please encourage friends and family to lend a hand. -

Portsmouth Number List 2016
Portsmouth Number List 2016 The RYA Portsmouth Yardstick Scheme is provided to enable clubs to allow boats of different classes to race against each other fairly. The RYA actively encourages clubs to adjust handicaps where classes are either under or over performing compared to the number being used. The Portsmouth Yardstick list combines the Portsmouth numbers with class configuration and the total number of races returned to the RYA in the annual return. This additional data has been provided to help clubs achieve the stated aims of the Portsmouth Yardstick system and make adjustments to Portsmouth Numbers where necessary. Clubs using the PN list should be aware that the list is based on the typical performance of each boat across a variety of clubs and locations. Experimental numbers are based on fewer returns and are to be used as a guide for clubs to allocate as a starting number before reviewing and adjusting where necessary. The list of experimental Portsmouth Numbers will be periodically reviewed by the RYA and is based on data received from the PY Online website (www.pys.org.uk). Users of the PY scheme are reminded that all Portsmouth Numbers published by the RYA should be regarded as a guide only. The RYA list is not definitive and clubs should adjust where necessary. For further information please visit the RYA website: http://www.rya.org.uk/racing/Pages/portsmouthyardstick.aspx RYA PN LIST - Dinghy Change Class Name No. of Crew Rig Spinnaker Number Races Notes from '15 420 2 S C 1105 0 278 2000 2 S A 1101 1 1967 29ER 2 S A -
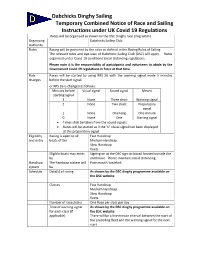
Dabchicks Dinghy Sailing Temporary Combined Notice of Race And
Dabchicks Dinghy Sailing Temporary Combined Notice of Race and Sailing Instructions under UK Covid 19 Regulations Races will be organised as shown by the DSC Dinghy race programme Organising Dabchicks Sailing Club Authority Rules Racing will be governed by the rules as defined in the Racing Rules of Sailing The relevant rules and bye-laws of Dabchicks Sailing Club (DSC) will apply. Races organised under Covid-19 conditions social distancing regulations. Please note it is the responsibility of participants and volunteers to abide by the Government Covid 19 regulations in force at that time. Rule Races will be started by using RRS 26 with the warning signal made 5 minutes changes before the start signal. or RRS 26 is changed as follows: Minutes before Visual signal Sound signal Means starting signal 3 None Three short Warning signal 2 None Two short Preparatory signal 1 None One long One minute 0 None One Starting signal Times shall be taken from the sound signals. Races will be started as if the ‘U’ visual signal had been displayed at the preparatory signal Eligibility Racing is open to all Fast Handicap and entry boats of the Medium Handicap Slow Handicap fleets Eligible boats may enter Signing on at the DSC sign on board located outside the by clubhouse. Please maintain social distancing Handicap The handicap system will Portsmouth Yardstick system be Schedule Date(s) of racing As shown by the DSC dinghy programme available on the DSC website Classes Fast Handicap Medium Handicap Slow Handicap fleets Number of races/class One Race -

2021 Boat Parking Fees
2021 Boat Parking Fees Fee payable: boat length x beam rounded to closest sq. m. Main compound: £9 per sq. m. Minster compound: £4.5 per sq. m. COST PER YEAR: Class Length Beam m2 MAIN compound MINSTER compound 29er 4.45 1.77 8 £72 £36 29erxx 4.45 1.77 8 £72 £36 420 4.2 1.71 7 £63 £32 470 4.7 1.68 8 £72 £36 49er 4.99 2.9 14 £126 £63 505 5.05 1.88 9 £81 £41 Access 2.3 2.3 1.25 3 £27 £14 Access 303 3.03 1.35 4 £36 £18 Albacore 4.57 1.53 7 £63 £32 B14 4.25 3.05 13 £117 £59 Blaze 4.2 2.48 10 £90 £45 Bobbin 2.74 1.27 3 £27 £14 Boss 4.9 2 10 £90 £45 Bosun 4.27 1.68 7 £63 £32 Buzz 4.2 1.92 8 £72 £36 Byte 3.65 1.3 5 £45 £23 Cadet 3.22 1.27 4 £36 £18 Catapult 5 2.25 11 £99 £50 Challenger Tri 4.57 3.5 16 £144 £72 Cherub 3.7 1.8 7 £63 £32 Comet 3.45 1.37 5 £45 £23 Comet Duo 3.57 1.52 5 £45 £23 Comet Mino 3.45 1.37 5 £45 £23 Comet Race 4.27 1.63 7 £63 £32 Comet Trio 4.6 1.83 8 £72 £36 Comet Versa 3.96 1.65 7 £63 £32 Comet XTRA 3.45 1.37 5 £45 £23 Comet Zero 3.45 1.42 5 £45 £23 Contender 4.87 1.5 7 £63 £32 Cruz 4.58 1.82 8 £72 £36 Dart 15 4.54 2.13 10 £90 £45 Dart 16 4.8 2.3 11 £99 £50 Dart 18 5.5 2.29 13 £117 £59 Dart Hawk 5.5 2.6 14 £126 £63 Enterprise 4.04 1.62 7 £63 £32 Escape 12 3.89 1.52 6 £54 £27 Escape Captiva 3.6 1.6 6 £54 £27 Escape Mango 2.9 1.2 3 £27 £14 Escape Playcat 4.8 2.1 10 £90 £45 Escape Rumba 3.9 1.6 6 £54 £27 Escape Solsa 2.9 1.2 3 £27 £14 Europe 3.38 1.41 5 £45 £23 F18 5.52 2.6 14 £126 £63 Finn 4.5 1.5 7 £63 £32 Fireball 4.93 1.37 7 £63 £32 Firefly 3.66 1.42 5 £45 £23 Flash 3.55 1.3 5 £45 £23 Flying Fifteen 6.1 1.54 9 £81 £41 -

Final Placings Place Boat Number Helm Crew 1 RS800 1219 Peter
Final Placings Place Boat Number Helm Crew 1 RS800 1219 Peter Barton Chris Feibusch 2 Fireball 15083 Chris Gill Adam Broughton 3 B14 795 Mark Barnes Charlotte Jones 4 Osprey 1116 Colin Stephens Mike Greig 5 RS800 1164 Russ Gibbs Jamie Dawson 6 RS400 411 Richard Cain 7 Merlin 3779 Dave Lee Tim Laws 8 RS200 1626 Edd Whitehead Edd Whitehead 9 Laser 210631 Ben Flower 10 Osprey 1356 Emma Stevenson Ben Hawkes 11 RS300 411 Steve Bolland 12 Merlin 3787 Chris Martin Jared Lewis 13 Fireball 14708 Colin Jarvis Derek Jarvis 14 Blaze 803 Hugh Kingdon 15 Fireball 14789 Hannah Showell James Beer 16 Phantom 14 Simon Hawkes 17 Hornet 2160 Nigel Skudder Keith Hills 18 RS400 727 Bob Warren Marianne Bryan 19 RS Aero 7 1632 Greg Bartlett 20 RS Aero 7 1930 Paul Bartlett 21 Blaze 710 Nick Ripley 22 RS400 6 Dave Stockton Paul Birbeck 23 B14 735 Tom Gatehouse Kate Gatehouse 24 RS400 1123 Dave Stubbs Paul Aitken 25 Supernova 1092 Ian Horlock 26 RS Aero 7 1397 Mark Pollard 27 Enterprise 21889 Thomas Kliskey Simon Lees 28 GP14 13146 Steve Ward 29 Blaze 797 Mike Holmes 30 Osprey 1357 Paul Roberts John Clark 31 Merlin 3713 Steve Harling Eleanor Thomas 32 Merlin 3544 David Downs Ros Downs 33 RS Aero 7 1817 Chris Jones 34 Merlin 3628 Robin Charles Dan Newman 35 Laser 200521 Martin Gibson 36 Phantom 1348 Richard Cumberbatch 37 Supernova 1168 Alistair Glen 38 Merlin 3757 Andy Postle Aidan Postle 39 Merlin 3721 Nick Turner Carly Gurr 40 Solo 5494 John Steels 41 Finn 666 Ian Jay 42 RS400 1287 James Bowman Andrew Gladstone 43 Laser 205791 Dan Newall 44 RS Aero 1312 Andrew