Matt Chiu, Eastman School of Music, "Putting the Math in Math Rock"
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Galapagos Momentum Press Quotes
Quotes from Upsilon Acrux’s Paul Lai, excerpted from Etan Rosenbloom’s “Mapping the path to obscurity” in Prefix Magazine, October 18, 2006: “We feel 7/4 the way that most people feel a 4/4 pocket. It's just a downbeat -- it's like you wanna rock, but so much shit is rocked in 4. And it's rad. But I can't do that shit again -- I'd like to hear something else. That's why I like Meshuggah and other bands that step out of the standard time signatures. “ “…we are a rock band, we just try not to do typical things. We listen to enough music, we're big enough music geeks, that we wouldn't want to play something cool that had already been done by ten thousand bands. It works in music and it works in art: If you have something to say, then say it in your own way. If you don't have anything to say, shut the fuck up, go home and be a consumer. … Most bands these days sound like they're working at Kinko's, just carbon copies of other bands. … … Ultimately, I'm looking for singularity. We strive for unprecedented music. …” “…I think Faust, especially, is one of the most creative bands ever: You can't really pinpoint what they exactly do. That's what all bands should strive for, creativity above genres or styles. It should be about trying to be as creative possible. … If you're not reaching out to someone, creating a personal bridge with lyrics and vocals,…then you should be insanely creative in a completely different way. -

MTO 17.3: Osborn, Understanding Through-Composition
KU ScholarWorks | http://kuscholarworks.ku.edu Please share your stories about how Open Access to this article benefits you. Understanding Through-Composition in Post- Rock, Math-Metal, and other Post-Millennial Rock Genres by Brad Osborn 2011 This is the published version of the article, made available with the permission of the publisher. The original published version can be found at the link below. Osborn, Brad. 2011. “Understanding Through-Composition in Post- Rock, Math-Metal, and other Post-Millennial Rock Genres.” Music Theory Online 17, no. 3 Published version: http://www.mtosmt.org/issues/mto.11.17.3/ mto.11.17.3.osborn.pdf Terms of Use: http://www2.ku.edu/~scholar/docs/license.shtml This work has been made available by the University of Kansas Libraries’ Office of Scholarly Communication and Copyright. Volume 17, Number 3, October 2011 Copyright © 2011 Society for Music Theory Understanding Through-Composition in Post-Rock, Math-Metal, and other Post-Millennial Rock Genres (1) Brad Osborn NOTE: The examples for the (text-only) PDF version of this item are available online at: http://www.mtosmt.org/issues/mto.11.17.3/mto.11.17.3.osborn.php KEYWORDS: form, through-composition, rock, experimental rock, post-millennial rock, art rock, post-rock, math-metal, progressive rock, Radiohead, Animal Collective, The Beatles ABSTRACT: Since the dawn of experimental rock’s second coming in the new millennium, experimental artists have begun distancing themselves from Top-40 artists through formal structures that eschew recapitulatory verse/chorus conventions altogether. In order to understand the correlation between genre and form more thoroughly, this paper provides a taxonomic approach to through-composition in several post-millennial experimental rock genres including post-rock, math-metal, art rock, and neo-prog. -
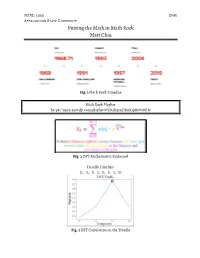
Putting the Math in Math Rock Matt Chiu
MTSE: 2020 Chiu Appalachian State University Putting the Math in Math Rock Matt Chiu Fig. 1 Math Rock Timeline Math Rock Playlist: https://open.spotify.com/playlist/0YMehqtnDK9X1pBsVc0ftN Fig. 2 DFT Mathematics Explained Tresillo Timeline: [1, 0, 0, 1, 0, 0, 1, 0] Fig. 3 DFT Calculation on the Tresillo MTSE: 2020 Chiu Appalachian State University ACCENT PROFILE RULES MPR 3: Event +1 wherever there is a note MPR 6: Bass Note +1 to lowest note of any 5 contiguous units PEC: Second of Two +1 to second to two adjacent notes PEC: Initial and Final Tones +1 to both ends of an adjacent string of notes Large Leaps +1 to any leap of 5 semitones or more +1 to all changes in the contour: contour is established after Continuous/Contour 2 moves in the same direction MPR 1: Parallelism +1 to parallelism projects PEC = Povel/Essens Clock (Rules) MPR = Metric Preference Rules (Lerdahl and Jackendoff) Fig. 4 Accent Profile Rule [5, 2, – 2, 2, 1, 1, 2, 1, 4, 1, 2, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 2, 1, 1] E . Gtr. œ œ œ œ œ œ œ œ œ œ œ (Lead) & œ œ œ œ œ œ œ œ œ œ œ œ œ œ ˙ œ j œ œ ˙ œ™ œ & ™ œ ˙ ™ J J ˙ ˙ & ˙ ˙ ˙ ˙ agnitude M Component ˙ ˙ œ Fig. 5 Never Meant: Guitar 1 (top); Rhythmic Profile (bottom) MTSE: 2020 Chiu Appalachian State University [4, 2, 2, 3, 1, 2, 1, 3, 2, 3, 3, 0, 0, 5, 2, 3, 1, 2, 1, 1, 4, 2, 2, 1] E. -

Brand New Cd & Dvd Releases 2006 6,400 Titles
BRAND NEW CD & DVD RELEASES 2006 6,400 TITLES COB RECORDS, PORTHMADOG, GWYNEDD,WALES, U.K. LL49 9NA Tel. 01766 512170: Fax. 01766 513185: www. cobrecords.com // e-mail [email protected] CDs, DVDs Supplied World-Wide At Discount Prices – Exports Tax Free SYMBOLS USED - IMP = Imports. r/m = remastered. + = extra tracks. D/Dble = Double CD. *** = previously listed at a higher price, now reduced Please read this listing in conjunction with our “ CDs AT SPECIAL PRICES” feature as some of the more mainstream titles may be available at cheaper prices in that listing. Please note that all items listed on this 2006 6,400 titles listing are all of U.K. manufacture (apart from Imports which are denoted IM or IMP). Titles listed on our list of SPECIALS are a mix of U.K. and E.C. manufactured product. We will supply you with whichever item for the price/country of manufacture you choose to order. ************************************************************************************************************* (We Thank You For Using Stock Numbers Quoted On Left) 337 AFTER HOURS/G.DULLI ballads for little hyenas X5 11.60 239 ANATA conductor’s departure B5 12.00 327 AFTER THE FIRE a t f 2 B4 11.50 232 ANATHEMA a fine day to exit B4 11.50 ST Price Price 304 AG get dirty radio B5 12.00 272 ANDERSON, IAN collection Double X1 13.70 NO Code £. 215 AGAINST ALL AUTHOR restoration of chaos B5 12.00 347 ANDERSON, JON animatioin X2 12.80 92 ? & THE MYSTERIANS best of P8 8.30 305 AGALAH you already know B5 12.00 274 ANDERSON, JON tour of the universe DVD B7 13.00 -

Shane Perlowin (Guitar), Derek Poteat (Bass), Sean Dail (Drums)
WHAT THE PRESS HAS SAID ABOUT: AHLEUCHATISTAS WHAT YOU WILL CUNEIFORM 2006 Line-up: Shane Perlowin (guitar), Derek Poteat (bass), Sean Dail (drums) “…hefty doses of prog rock shock therapy… like the Magic Band on steroids. …these young lads convey boundless energy amid some unrelenting quirks and knotty time signatures, where meter and momentum are apt to change on a nanosecond’s notice. Diehard progressive rock junkies should enjoy the heck out of this little gem.” – Glen Astarita, All About Jazz, February 2006, www.allaboutjazz.com “…you owe it to yourself to hear this wonderful new recording from the Ahleuchatistas (great band name – think Charlie Parker, y’all). These three youngsters seem to be channeling the spirits of Fred Frith, Bill Laswell and Fred Maher, who recorded a similarly funky, spiky and fun album in 1981 under the name Massacre. Difficult, yes, but challenging, no – for all its weird jumpiness, this is friendly and inviting music that will be sure to have your patrons nodding their heads and tapping their feet. Granted, they’ll be tapping in 15/8 time, but still.” – Rick Anderson, CD Hot List: New Releases for Libraries, April 2006, cdhotlist.btol.com “This…trio’s math rock is a series of screeds against war, for human rights, even corporate malfeasance. The nuance: There are no words. …A free- jazz stepchild of Don Caballero, Ahleuchatistas have more swerves, rougher time changes, mini-improvisational sections and not a hint of distortion or studio trickery. On opener “Remember Rumsfeld at Abu Ghraib,” bass and drum roll over aloof guitars, acting as communiqués between the Pentagon and Iraq… “Shell in Ogoniland,” about the oil company’s mistreatment of people in Niger, sounds like the gurgling of a viscous liquid…created by a sludge-like bass groove and doubled bass drum kicks. -

America's Hardcore.Indd 278-279 5/20/10 9:28:57 PM Our First Show at an Amherst Youth Center
our first show at an Amherst youth center. Scott Helland’s brother Eric’s band Mace played; they became The Outpatients. Our first Boston show was with DYS, The Mighty COs and The AMERICA’S HARDCORE FU’s. It was very intense for us. We were so intimidated. Future generations will fuck up again THE OUTPATIENTS got started in 1982 by Deep Wound bassist Scott Helland At least we can try and change the one we’re in and his older brother Eric “Vis” Helland, guitarist/vocalist of Mace — a 1980-82 — Deep Wound, “Deep Wound” Metal group that played like Motörhead but dug Black Flag (a rare blend back then). The Outpatients opened for bands like EAST COAST Black Flag, Hüsker Dü and SSD. Flipside called ’em “one of the most brutalizing live bands In 1980, over-with small cities and run-down mill towns across the Northeast from the period.” 1983’s gnarly Basement Tape teemed with bored kids with nothing to do. Punk of any kind earned a cultural demo included credits that read: “Play loud in death sentence in the land of stiff upper-lipped Yanks. That cultural isolation math class.” became the impetus for a few notable local Hardcore scenes. CANCEROUS GROWTH started in 1982 in drummer Charlie Infection’s Burlington, WESTERN MASSACHUSETTS MA bedroom, and quickly spread across New had an active early-80s scene of England. They played on a few comps then 100 or so inspired kids. Western made 1985’s Late For The Grave LP in late 1984 Mass bands — Deep Wound, at Boston’s Radiobeat Studios (with producer The Outpatients, Pajama Slave Steve Barry). -

Teacher Biographies
0 Teacher Biographies Guitar & Bass Teachers Eric Brewer ...................................................................................................... 1 Chris Bumbera ................................................................................................. 2 Mike Dattilo ..................................................................................................... 3 Preston Lindey ................................................................................................. 4 Stephen Maynard ............................................................................................. 5 Dan Monacella ................................................................................................. 7 Mike Moore ..................................................................................................... 8 Zack Orr ........................................................................................................... 9 Drum Teachers Steve Barone .................................................................................................. 10 Tory Shatto .................................................................................................... 11 Brian Strobel .................................................................................................. 12 Band & Orchestra Teachers Jim Caspar ..................................................................................................... 13 Elva Newcomer-Kocher ............................................................................... -

Xiami Music Genre 文档
xiami music genre douban 2021 年 02 月 14 日 Contents: 1 目录 3 2 23 3 流行 Pop 25 3.1 1. 国语流行 Mandarin Pop ........................................ 26 3.2 2. 粤语流行 Cantopop .......................................... 26 3.3 3. 欧美流行 Western Pop ........................................ 26 3.4 4. 电音流行 Electropop ......................................... 27 3.5 5. 日本流行 J-Pop ............................................ 27 3.6 6. 韩国流行 K-Pop ............................................ 27 3.7 7. 梦幻流行 Dream Pop ......................................... 28 3.8 8. 流行舞曲 Dance-Pop ......................................... 29 3.9 9. 成人时代 Adult Contemporary .................................... 29 3.10 10. 网络流行 Cyber Hit ......................................... 30 3.11 11. 独立流行 Indie Pop ......................................... 30 3.12 12. 女子团体 Girl Group ......................................... 31 3.13 13. 男孩团体 Boy Band ......................................... 32 3.14 14. 青少年流行 Teen Pop ........................................ 32 3.15 15. 迷幻流行 Psychedelic Pop ...................................... 33 3.16 16. 氛围流行 Ambient Pop ....................................... 33 3.17 17. 阳光流行 Sunshine Pop ....................................... 34 3.18 18. 韩国抒情歌曲 Korean Ballad .................................... 34 3.19 19. 台湾民歌运动 Taiwan Folk Scene .................................. 34 3.20 20. 无伴奏合唱 A cappella ....................................... 36 3.21 21. 噪音流行 Noise Pop ......................................... 37 3.22 22. 都市流行 City Pop ......................................... -

Mise En Page 1
www.sonicprotest.com Jamais trois sans quatre comme dit si bien Peugeot et donc logiquement : Sonic Protest 2006, du 4 au 7 mai : youpi. C’est une ouverture facile mais puisque même la Vache qui rit s’y est mis.... (pour contacter la régie publicitaire, merci de passer par notre site) Bref, depuis 2003, la micro équipe de Sonic Protest se réunit souvent, avec plaisir et sans rancune, pour qu’au rythme exténuant d’une fois l’an, on puisse voir et entendre des tentatives de musique vivante dans des lieux vivables. C’est un vrai luxe puisque ça n’a l’air de rien. Et puisque ça n’a l’air de rien, ça ne se donne pas l’air, ça ne pompe pas. Ca, c’est Sonic Protest : une collection précieuse de concerts qui ne se ressemblent pas ; une réunion d’artistes qui ont du style, loin des genres ; un fatras de moments qui se partagent avec joie et ne se consomment pas. Sonic Protest n’aime vraiment pas l’autoroute et roule donc sur la bordure des petits chemins, plus chaotiques et plus propices aux cascades et aux rencontres. Une nouvelle station service d’ailleurs cette année puisqu’aux partenaires de toujours (LES Instants Chavirés) et aux collaborateurs de moins en moins éphémères (Mains d’Oeuvres), et c’est tant mieux, s’ajoute désormais l'Espace 1789, histoire d’abolir les privilégiés, cette fois. Pour continuer dans le vroum-vroum, Sonic Protest carbure toujours au mélange free-harsh-lo-fi- fartcore-psyche-drone-folk-garage-math’n’roll et enrichit même sa formule en distillant des projections de films et des performances garanties 100% sans musiciens. -

Excerpts from What the Press Has Said About
Excerpts from what the press has said about some of Cheer-Accident’s past releases: WHAT SEQUEL? 2006 PRAVDA Featuring: Scott Ashley (Guitar), Thymme Jones (Vocals, Drums, Clarinet, Trumpet, Recorder, various keyboard instruments), Jeff Libersher (Bass, Guitar, Piano, Trumpet, bg. Vocals), John McEntire (Overdubs, Mixing), Julie Pomerleau (Violin), Jessica Ruffins (Engineer), Toby Summerfield (Double Bass) “Cheer-Accident seems to thrive on the contradictions of experimental music. For every straight-ahead piano-driven pop number there's a song flailing hard rock riffs with abandon, and usually these two opposing genres are place right next to one another. …the group does an admirable job synthesizing an avant-garde pop collection from decades old indie rock basics and eccentric asides. There are shades of Pavement, Unwound and Sonic Youth in the slightly atonal slacker guitar strum on "Keep in Touch," the pogoing chorus punctuation seems particularly Malkmus-ian. "Go Gone Green" has a great drive of '70s prog/jazz... Jesus Lizard skronk spreads out all over "Surviving a Methodology;" chugging guitars cut a sinister path through a rhythm section bent on strange time signatures. …as an album of '90s fringe indie rock revisited, it's a fine statement.” – Aaron Shaul, Ink 19, July 2007, www.ink19.com “… Cheer-Accident has been dirtying their hands in some form or another for over twenty-years and it’s obvious that music is the fruit of their hard work. … What Sequel? finds the band actually introducing the word “concise” into their terminology, thanks in large part to the efforts of producer John McEntire (Tortoise, The Sea And Cake). -

Issue 161.Pmd
email: [email protected] website: nightshift.oxfordmusic.net Free every month. NIGHTSHIFT Issue 161 December Oxford’s Music Magazine 2008 Flying Fish! Little Fish on their crazy year inside NIGHTSHIFT: PO Box 312, Kidlington, OX5 1ZU. Phone: 01865 372255 NEWNEWSS Nightshift: PO Box 312, Kidlington, OX5 1ZU Phone: 01865 372255 email: [email protected] Online: nightshift.oxfordmusic.net THE ACADEMY will be renamed pub is currently owned by Greene the O2 Academy from 1st January King and they are searching for a 2009 after a partnership deal was new manager but as of yet struck between the mobile network everything is up in the air and the company and Live Nation, the current area manager is said not to majority shareholder company in be keen on live music. the Academy Music Group. The deal Allison Young, who has promoted follows on from Carling’s gigs at the Port, on St Clement’s, YOUNG KNIVES’ HENRY DARTNALL has been talking to Nightshift sponsorship of the venue expiring. for the last three and a half years about the band’s special ‘Homecoming’ gig at the Academy on Sunday A press release documenting the told Nightshift, “Our last night at 21st December, and his pride in the band’s acclaimed ‘Suprerabundance’ new partnership declared that “O2 the Port Mahon is on the 2nd album, released earlier this year. The Oxford show is part of a series of customers will gain priority access December. We are aware that there Academy Homecoming gigs at cities around the UK and will see Young to tickets to all gigs at the venues, is someone interested in the place; Knives taking over the entire venue and picking some of their favourite as well as other Live Nation events they, however, want to change it bands as support. -

Riff Schemes, Form, and the Genre of Early American Hardcore Punk (1978–83) * David B
Volume 21, Number 1, March 2015 Copyright © 2015 Society for Music Theory Riff Schemes, Form, and the Genre of Early American Hardcore Punk (1978–83) * David B. Easley NOTE: The examples for the (text-only) PDF version of this item are available online at: http://www.mtosmt.org/issues/mto.15.21.1/mto.15.21.1.easley.php KEYWORDS: punk rock, hardcore, genre, popular music, riff, repetition, form, musical meaning, Bad Brains, Black Flag, Dead Kennedys, Minor Threat ABSTRACT: This article explores the structures of guitar riffs in early American hardcore punk rock and their role in the creation of meaning within the genre. Drawing upon a corpus analysis of recordings by Bad Brains, Black Flag, Dead Kennedys, and Minor Threat, the article begins by outlining the main ways in which guitar riffs are structured. Many reflect a structural basis in what I call “riff schemes,” organizing patterns of physical repetition and physical change made by a guitarist’s fretting hand. There are four main types, which are defined by the location of repetition within the riff (at the beginning or at the end) and whether the type of repetition is exact or altered: (1) Initial Repetition and Contrast, (2) Statement and Terminal Repetition, (3) Statement and Terminal Alteration, and (4) Model and Sequential Repetition. These schemes may also play an expressive role in song narratives of energy, intensity, and aggression, all of which are common tropes in oral histories of hardcore. In the final part of the article, I present analyses of two songs that demonstrate this use: Minor Threat’s “Straight Edge” and Black Flag’s “Rise Above.” Received July 2014 Introduction [1.1] American hardcore punk rock—or simply “hardcore”—is a subgenre of punk that first emerged in the late 1970s as a response to the “punk rock revolution” created by bands such as the Sex Pistols and the Ramones ( Blush 2010 , 14).