DOCSLIB.ORG

Lecture 12 Heteroscedasticity

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 12 Heteroscedasticity RS – Lecture 12 Lecture 12 Heteroscedasticity 1 Two-Step Estimation of the GR Model: Review • Use the GLS estimator with an estimate of 1. is parameterized by a few estimable parameters, = (θ). Example: Harvey’s heteroscedastic model. 2. Iterative estimation procedure: (a) Use OLS residuals to estimate the variance function. (b) Use the estimated in GLS - Feasible GLS, or FGLS. • True GLS estimator -1 -1 -1 bGLS = (X’Ω X) X’Ω y (converges in probability to .) • We seek a vector which converges to the same thing that this does. Call it FGLS, based on [X -1 X]-1 X-1 y 1 RS – Lecture 12 Two-Step Estimation of the GR Model: Review Two-Step Estimation of the GR Model: FGLS • Feasible GLS is based on finding an estimator which has the same properties as the true GLS. 2 Example: Var[i] = Exp(zi). True GLS: Regress yi/[ Exp((1/2)zi)] on xi/[ Exp((1/2)zi)] FGLS: With a consistent estimator of [,], say [s,c], we do the same computation with our estimates. Note: If plim [s,c] = [,], then, FGLS is as good as true GLS. • Remark: To achieve full efficiency, we do not need an efficient estimate of the parameters in , only a consistent one. 2 RS – Lecture 12 Heteroscedasticity • Assumption (A3) is violated in a particular way: has unequal variances, but i and j are still not correlated with each other. Some observations (lower variance) are more informative than others (higher variance). f(y|x) . E(y|x) = b0 + b1x . x1 x2 x3 x 5 Heteroscedasticity • Now, we have the CLM regression with hetero-(different) scedastic (variance) disturbances. (A1) DGP: y = X + is correctly specified. (A2) E[|X] = 0 2 (A3’) Var[i] = i, i > 0. (CLM => i = 1, for all i.) (A4) X has full column rank – rank(X)=k-, where T ≥ k. 2 • Popular normalization: i i = 1. (A scaling, absorbed into .) • A characterization of the heteroscedasticity: Well defined estimators and methods for testing hypotheses will be obtainable if the heteroscedasticity is “well behaved” in the sense that i / i i → 0 as T → . -i.e., no single observation becomes dominant. (1/T)i i → some stable constant. (Not a plim!) 3 RS – Lecture 12 GR Model and Testing • Implications for conventional OLS and hypothesis testing: 1. b is still unbiased. 2. Consistent? We need the more general proof. Not difficult. 3. If plim b = , then plim s2 = 2 (with the normalization). 4. Under usual assumptions, we have asymptotic normality. • Two main problems with OLS estimation under heterocedasticity: (1) The usual standard errors are not correct. (They are biased!) (2) OLS is not BLUE. • Since the standard errors are biased, we cannot use the usual t- statistics or F --statistics or LM statistics for drawing inferences. This is a serious issue. Heteroscedasticity: Inference Based on OLS • Q: But, what happens if we still use s2(XX)-1? A: It depends on XX - XX. If they are nearly the same, the OLS covariance matrix will give OK inferences. But, when will XX - XX be nearly the same? The answer is based on a property of weighted averages. Suppose i is randomly drawn from a distribution with E[i] = 1. Then, 2 p 2 2 (1/T)i i xi E[x ] --just like (1/T)i xi . • Remark: For the heteroscedasticity to be a significant issue for estimation and inference by OLS, the weights must be correlated with 2 x and/or xi . The higher correlation, heteroscedasticity becomes more important (b is more inefficient). 4 RS – Lecture 12 Finding Heteroscedasticity • There are several theoretical reasons why the i may be related to x 2 and/or xi : 1. Following the error-learning models, as people learn, their errors of 2 behavior become smaller over time. Then, σ i is expected to decrease. 2 2. As data collecting techniques improve, σ i is likely to decrease. Companies with sophisticated data processing techniques are likely to commit fewer errors in forecasting customer’s orders. 3. As incomes grow, people have more discretionary income and, thus, 2 more choice about how to spend their income. Hence, σ i is likely to increase with income. 4. Similarly, companies with larger profits are expected to show greater variability in their dividend/buyback policies than companies with lower profits. Finding Heteroscedasticity • Heteroscedasticity can also be the result of model misspecification. • It can arise as a result of the presence of outliers (either very small or very large). The inclusion/exclusion of an outlier, especially if T is small, can affect the results of regressions. • Violations of (A1) --model is correctly specified--, can produce heteroscedasticity, due to omitted variables from the model. • Skewness in the distribution of one or more regressors included in the model can induce heteroscedasticity. Examples are economic variables such as income, wealth, and education. • David Hendry notes that heteroscedasticity can also arise because of – (1) incorrect data transformation (e.g., ratio or first difference transformations). – (2) incorrect functional form (e.g., linear vs log–linear models). 5 RS – Lecture 12 Finding Heteroscedasticity • Heteroscedasticity is usually modeled using one the following specifications: 2 2 2 - H1 : σt is a function of past εt and past σt (GARCH model). 2 -H2 : σt increases monotonically with one (or several) exogenous variable(s) (x1,, . , xT ). 2 -H3 : σt increases monotonically with E(yt). 2 -H4 : σt is the same within p subsets of the data but differs across the subsets (grouped heteroscedasticity). This specification allows for structural breaks. • These are the usual alternatives hypothesis in the heteroscedasticity tests. Finding Heteroscedasticity • Visual test In a plot of residuals against dependent variable or other variable will often produce a fan shape. 180 160 140 120 100 Series1 80 60 40 20 0 050100150 12 6 RS – Lecture 12 Testing for Heteroscedasticity • Usual strategy when heteroscedasticity is suspected: Use OLS along the White estimator. This will give us consistent inferences. • Q: Why do we want to test for heteroscedasticity? A: OLS is no longer efficient. There is an estimator with lower asymptotic variance (the GLS/FGLS estimator). 2 2 2 • We want to test: H0: E(ε |x1, x2,…, xk) = E(ε ) = 2 2 2 • The key is whether E[ ] = i is related to x and/or xi . Suppose we suspect a particular independent variable, say X1, is driving i. • Then, a simple test: Check the RSS for large values of X1, and the RSS for small values of X1. This is the Goldfeld-Quandt test. Testing for Heteroscedasticity • The Goldfeld-Quandt test - Step 1. Arrange the data from small to large values of the independent variable suspected of causing heteroscedasticity, Xj. - Step 2. Run two separate regressions, one for small values of Xj and one for large values of Xj, omitting d middle observations (≈ 20%). Get the RSS for each regression: RSS1 for small values of Xj and RSS2 for large Xj’s. - Step 3. Calculate the F ratio GQ = RSS2/RSS1, ~ Fdf,df with df =[(T – d) – 2(k+1)]/2 (A5 holds). If (A5) does not hold, we have GQ is asymptoticallly χ2. 7 RS – Lecture 12 Testing for Heteroscedasticity • The Goldfeld-Quandt test Note: When we suspect more than one variable is driving the i’s, this test is not very useful. • But, the GQ test is a popular to test for structural breaks (two regimes) in variance. For these tests, we rewrite step 3 to allow for different size in the sub-samples 1 and 2. - Step 3. Calculate the F-test ratio GQ = [RSS2/ (T2 – k)]/[RSS1/ (T1 – k)] Testing for Heteroscedasticity: LR Test • The Likelihood Ratio Test Let’s define the likelihood function, assuming normality, for a general case, where we have g different variances: g g T T 1 1 ln L ln2 i ln2 (y X )(y X ) i 2 i i i i 2 i1 2 2 i1 i We have two models: 2 2 (R) Restricted under H0: i = . From this model, we calculate ln L T T ln L [ln(2) 1] ln(ˆ 2 ) R 2 2 (U) Unrestricted. From this model, we calculate the log likelihood. g T Ti 2 2 1 ln LU [ln(2) 1] lnˆ i ; ˆ i (yi X ib)(yi X ib) 2 2 Ti i1 8 RS – Lecture 12 Testing for Heteroscedasticity: LR Test • Now, we can estimate the Likelihood Ratio (LR) test: g ˆ 2 ˆ 2 a 2 LR 2(ln LU ln LR ) T ln Ti lni g1 i1 2 Under the usual regularity conditions, LR is approximated by a χ g-1. 2 • Using specific functions for i , this test has been used by Rutemiller and Bowers (1968) and in Harvey’s (1976) groupwise heteroscedasticity paper. Testing for Heteroscedasticity • Score LM tests 2 2 • We want to develop tests of H0: E(ε |x1, x2,…, xk) = against an H1 with a general functional form. 2 2 • Recall the central issue is whether E[ ] = i is related to x 2 and/or xi . Then, a simple strategy is to use OLS residuals to estimate 2 2 disturbances and look for relationships between ei and xi and/or xi . • Suppose that the relationship between ε2 and X is linear: ε2 = Xα + v Then, we test: H0: α = 0 against H1: α ≠ 0. • We can base the test on how the squared OLS residuals e correlate with X. 9 RS – Lecture 12 Testing for Heteroscedasticity • Popular heteroscedasticity LM tests: - Breusch and Pagan (1979)’s LM test (BP). - White (1980)’s general test. • Both tests are based on OLS residuals. That is, calculated under H0: No heteroscedasticity.
Load more

Recommended publications
  • Hypothesis Testing and Likelihood Ratio Tests
    Hypottthesiiis tttestttiiing and llliiikellliiihood ratttiiio tttesttts Y We will adopt the following model for observed data. The distribution of Y = (Y1, ..., Yn) is parameter considered known except for some paramett er ç, which may be a vector ç = (ç1, ..., çk); ç“Ç, the paramettter space. The parameter space will usually be an open set. If Y is a continuous random variable, its probabiiillliiittty densiiittty functttiiion (pdf) will de denoted f(yy;ç) . If Y is y probability mass function y Y y discrete then f(yy;ç) represents the probabii ll ii tt y mass functt ii on (pmf); f(yy;ç) = Pç(YY=yy). A stttatttiiistttiiicalll hypottthesiiis is a statement about the value of ç. We are interested in testing the null hypothesis H0: ç“Ç0 versus the alternative hypothesis H1: ç“Ç1. Where Ç0 and Ç1 ¶ Ç. hypothesis test Naturally Ç0 § Ç1 = ∅, but we need not have Ç0 ∞ Ç1 = Ç. A hypott hesii s tt estt is a procedure critical region for deciding between H0 and H1 based on the sample data. It is equivalent to a crii tt ii call regii on: a critical region is a set C ¶ Rn y such that if y = (y1, ..., yn) “ C, H0 is rejected. Typically C is expressed in terms of the value of some tttesttt stttatttiiistttiiic, a function of the sample data. For µ example, we might have C = {(y , ..., y ): y – 0 ≥ 3.324}. The number 3.324 here is called a 1 n s/ n µ criiitttiiicalll valllue of the test statistic Y – 0 . S/ n If y“C but ç“Ç 0, we have committed a Type I error.
    [Show full text]
  • Lecture 22: Bivariate Normal Distribution Distribution
    6.5 Conditional Distributions General Bivariate Normal Let Z1; Z2 ∼ N (0; 1), which we will use to build a general bivariate normal Lecture 22: Bivariate Normal Distribution distribution. 1 1 2 2 f (z1; z2) = exp − (z1 + z2 ) Statistics 104 2π 2 We want to transform these unit normal distributions to have the follow Colin Rundel arbitrary parameters: µX ; µY ; σX ; σY ; ρ April 11, 2012 X = σX Z1 + µX p 2 Y = σY [ρZ1 + 1 − ρ Z2] + µY Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 1 / 22 6.5 Conditional Distributions 6.5 Conditional Distributions General Bivariate Normal - Marginals General Bivariate Normal - Cov/Corr First, lets examine the marginal distributions of X and Y , Second, we can find Cov(X ; Y ) and ρ(X ; Y ) Cov(X ; Y ) = E [(X − E(X ))(Y − E(Y ))] X = σX Z1 + µX h p i = E (σ Z + µ − µ )(σ [ρZ + 1 − ρ2Z ] + µ − µ ) = σX N (0; 1) + µX X 1 X X Y 1 2 Y Y 2 h p 2 i = N (µX ; σX ) = E (σX Z1)(σY [ρZ1 + 1 − ρ Z2]) h 2 p 2 i = σX σY E ρZ1 + 1 − ρ Z1Z2 p 2 2 Y = σY [ρZ1 + 1 − ρ Z2] + µY = σX σY ρE[Z1 ] p 2 = σX σY ρ = σY [ρN (0; 1) + 1 − ρ N (0; 1)] + µY = σ [N (0; ρ2) + N (0; 1 − ρ2)] + µ Y Y Cov(X ; Y ) ρ(X ; Y ) = = ρ = σY N (0; 1) + µY σX σY 2 = N (µY ; σY ) Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 2 / 22 Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 3 / 22 6.5 Conditional Distributions 6.5 Conditional Distributions General Bivariate Normal - RNG Multivariate Change of Variables Consequently, if we want to generate a Bivariate Normal random variable Let X1;:::; Xn have a continuous joint distribution with pdf f defined of S.
    [Show full text]
  • Generalized Linear Models and Generalized Additive Models
    00:34 Friday 27th February, 2015 Copyright ©Cosma Rohilla Shalizi; do not distribute without permission updates at http://www.stat.cmu.edu/~cshalizi/ADAfaEPoV/ Chapter 13 Generalized Linear Models and Generalized Additive Models [[TODO: Merge GLM/GAM and Logistic Regression chap- 13.1 Generalized Linear Models and Iterative Least Squares ters]] [[ATTN: Keep as separate Logistic regression is a particular instance of a broader kind of model, called a gener- chapter, or merge with logis- alized linear model (GLM). You are familiar, of course, from your regression class tic?]] with the idea of transforming the response variable, what we’ve been calling Y , and then predicting the transformed variable from X . This was not what we did in logis- tic regression. Rather, we transformed the conditional expected value, and made that a linear function of X . This seems odd, because it is odd, but it turns out to be useful. Let’s be specific. Our usual focus in regression modeling has been the condi- tional expectation function, r (x)=E[Y X = x]. In plain linear regression, we try | to approximate r (x) by β0 + x β. In logistic regression, r (x)=E[Y X = x] = · | Pr(Y = 1 X = x), and it is a transformation of r (x) which is linear. The usual nota- tion says | ⌘(x)=β0 + x β (13.1) · r (x) ⌘(x)=log (13.2) 1 r (x) − = g(r (x)) (13.3) defining the logistic link function by g(m)=log m/(1 m). The function ⌘(x) is called the linear predictor. − Now, the first impulse for estimating this model would be to apply the transfor- mation g to the response.
    [Show full text]
  • Data 8 Final Stats Review
    Data 8 Final Stats review I. Hypothesis Testing Purpose: To answer a question about a process or the world by testing two hypotheses, a null and an alternative. Usually the null hypothesis makes a statement that “the world/process works this way”, and the alternative hypothesis says “the world/process does not work that way”. Examples: Null: “The customer was not cheating-his chances of winning and losing were like random tosses of a fair coin-50% chance of winning, 50% of losing. Any variation from what we expect is due to chance variation.” Alternative: “The customer was cheating-his chances of winning were something other than 50%”. Pro tip: You must be very precise about chances in your hypotheses. Hypotheses such as “the customer cheated” or “Their chances of winning were normal” are vague and might be considered incorrect, because you don’t state the exact chances associated with the events. Pro tip: Null hypothesis should also explain differences in the data. For example, if your hypothesis stated that the coin was fair, then why did you get 70 heads out of 100 flips? Since it’s possible to get that many (though not expected), your null hypothesis should also contain a statement along the lines of “Any difference in outcome from what we expect is due to chance variation”. Steps: 1) Precisely state your null and alternative hypotheses. 2) Decide on a test statistic (think of it as a general formula) to help you either reject or fail to reject the null hypothesis. • If your data is categorical, a good test statistic might be the Total Variation Distance (TVD) between your sample and the distribution it was drawn from.
    [Show full text]
  • Stochastic Process - Introduction
    Stochastic Process - Introduction • Stochastic processes are processes that proceed randomly in time. • Rather than consider fixed random variables X, Y, etc. or even sequences of i.i.d random variables, we consider sequences X0, X1, X2, …. Where Xt represent some random quantity at time t. • In general, the value Xt might depend on the quantity Xt-1 at time t-1, or even the value Xs for other times s < t. • Example: simple random walk . week 2 1 Stochastic Process - Definition • A stochastic process is a family of time indexed random variables Xt where t belongs to an index set. Formal notation, { t : ∈ ItX } where I is an index set that is a subset of R. • Examples of index sets: 1) I = (-∞, ∞) or I = [0, ∞]. In this case Xt is a continuous time stochastic process. 2) I = {0, ±1, ±2, ….} or I = {0, 1, 2, …}. In this case Xt is a discrete time stochastic process. • We use uppercase letter {Xt } to describe the process. A time series, {xt } is a realization or sample function from a certain process. • We use information from a time series to estimate parameters and properties of process {Xt }. week 2 2 Probability Distribution of a Process • For any stochastic process with index set I, its probability distribution function is uniquely determined by its finite dimensional distributions. •The k dimensional distribution function of a process is defined by FXX x,..., ( 1 x,..., k ) = P( Xt ≤ 1 ,..., xt≤ X k) x t1 tk 1 k for anyt 1 ,..., t k ∈ I and any real numbers x1, …, xk .
    [Show full text]
  • Variance Function Regressions for Studying Inequality
    Variance Function Regressions for Studying Inequality The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Western, Bruce and Deirdre Bloome. 2009. Variance function regressions for studying inequality. Working paper, Department of Sociology, Harvard University. Citable link http://nrs.harvard.edu/urn-3:HUL.InstRepos:2645469 Terms of Use This article was downloaded from Harvard University’s DASH repository, and is made available under the terms and conditions applicable to Open Access Policy Articles, as set forth at http:// nrs.harvard.edu/urn-3:HUL.InstRepos:dash.current.terms-of- use#OAP Variance Function Regressions for Studying Inequality Bruce Western1 Deirdre Bloome Harvard University January 2009 1Department of Sociology, 33 Kirkland Street, Cambridge MA 02138. E-mail: [email protected]. This research was supported by a grant from the Russell Sage Foundation. Abstract Regression-based studies of inequality model only between-group differ- ences, yet often these differences are far exceeded by residual inequality. Residual inequality is usually attributed to measurement error or the in- fluence of unobserved characteristics. We present a regression that in- cludes covariates for both the mean and variance of a dependent variable. In this model, the residual variance is treated as a target for analysis. In analyses of inequality, the residual variance might be interpreted as mea- suring risk or insecurity. Variance function regressions are illustrated in an analysis of panel data on earnings among released prisoners in the Na- tional Longitudinal Survey of Youth. We extend the model to a decomposi- tion analysis, relating the change in inequality to compositional changes in the population and changes in coefficients for the mean and variance.
    [Show full text]
  • The Detection of Heteroscedasticity in Regression Models for Psychological Data
    Psychological Test and Assessment Modeling, Volume 58, 2016 (4), 567-592 The detection of heteroscedasticity in regression models for psychological data Andreas G. Klein1, Carla Gerhard2, Rebecca D. Büchner2, Stefan Diestel3 & Karin Schermelleh-Engel2 Abstract One assumption of multiple regression analysis is homoscedasticity of errors. Heteroscedasticity, as often found in psychological or behavioral data, may result from misspecification due to overlooked nonlinear predictor terms or to unobserved predictors not included in the model. Although methods exist to test for heteroscedasticity, they require a parametric model for specifying the structure of heteroscedasticity. The aim of this article is to propose a simple measure of heteroscedasticity, which does not need a parametric model and is able to detect omitted nonlinear terms. This measure utilizes the dispersion of the squared regression residuals. Simulation studies show that the measure performs satisfactorily with regard to Type I error rates and power when sample size and effect size are large enough. It outperforms the Breusch-Pagan test when a nonlinear term is omitted in the analysis model. We also demonstrate the performance of the measure using a data set from industrial psychology. Keywords: Heteroscedasticity, Monte Carlo study, regression, interaction effect, quadratic effect 1Correspondence concerning this article should be addressed to: Prof. Dr. Andreas G. Klein, Department of Psychology, Goethe University Frankfurt, Theodor-W.-Adorno-Platz 6, 60629 Frankfurt; email: [email protected] 2Goethe University Frankfurt 3International School of Management Dortmund Leipniz-Research Centre for Working Environment and Human Factors 568 A. G. Klein, C. Gerhard, R. D. Büchner, S. Diestel & K. Schermelleh-Engel Introduction One of the standard assumptions underlying a linear model is that the errors are inde- pendently identically distributed (i.i.d.).
    [Show full text]
  • LSAR: Efficient Leverage Score Sampling Algorithm for the Analysis
    LSAR: Efficient Leverage Score Sampling Algorithm for the Analysis of Big Time Series Data Ali Eshragh∗ Fred Roostay Asef Nazariz Michael W. Mahoneyx December 30, 2019 Abstract We apply methods from randomized numerical linear algebra (RandNLA) to de- velop improved algorithms for the analysis of large-scale time series data. We first develop a new fast algorithm to estimate the leverage scores of an autoregressive (AR) model in big data regimes. We show that the accuracy of approximations lies within (1 + O (")) of the true leverage scores with high probability. These theoretical results are subsequently exploited to develop an efficient algorithm, called LSAR, for fitting an appropriate AR model to big time series data. Our proposed algorithm is guaranteed, with high probability, to find the maximum likelihood estimates of the parameters of the underlying true AR model and has a worst case running time that significantly im- proves those of the state-of-the-art alternatives in big data regimes. Empirical results on large-scale synthetic as well as real data highly support the theoretical results and reveal the efficacy of this new approach. 1 Introduction A time series is a collection of random variables indexed according to the order in which they are observed in time. The main objective of time series analysis is to develop a statistical model to forecast the future behavior of the system. At a high level, the main approaches for this include the ones based on considering the data in its original time domain and arXiv:1911.12321v2 [stat.ME] 26 Dec 2019 those arising from analyzing the data in the corresponding frequency domain [31, Chapter 1].
    [Show full text]
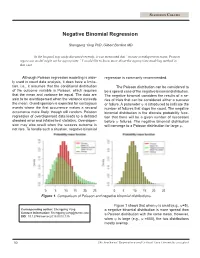
  • Negative Binomial Regression
    STATISTICS COLUMN Negative Binomial Regression Shengping Yang PhD ,Gilbert Berdine MD In the hospital stay study discussed recently, it was mentioned that “in case overdispersion exists, Poisson regression model might not be appropriate.” I would like to know more about the appropriate modeling method in that case. Although Poisson regression modeling is wide- regression is commonly recommended. ly used in count data analysis, it does have a limita- tion, i.e., it assumes that the conditional distribution The Poisson distribution can be considered to of the outcome variable is Poisson, which requires be a special case of the negative binomial distribution. that the mean and variance be equal. The data are The negative binomial considers the results of a se- said to be overdispersed when the variance exceeds ries of trials that can be considered either a success the mean. Overdispersion is expected for contagious or failure. A parameter ψ is introduced to indicate the events where the first occurrence makes a second number of failures that stops the count. The negative occurrence more likely, though still random. Poisson binomial distribution is the discrete probability func- regression of overdispersed data leads to a deflated tion that there will be a given number of successes standard error and inflated test statistics. Overdisper- before ψ failures. The negative binomial distribution sion may also result when the success outcome is will converge to a Poisson distribution for large ψ. not rare. To handle such a situation, negative binomial 0 5 10 15 20 25 0 5 10 15 20 25 Figure 1. Comparison of Poisson and negative binomial distributions.
    [Show full text]
  • Heteroscedastic Errors
    Heteroscedastic Errors ◮ Sometimes plots and/or tests show that the error variances 2 σi = Var(ǫi ) depend on i ◮ Several standard approaches to fixing the problem, depending on the nature of the dependence. ◮ Weighted Least Squares. ◮ Transformation of the response. ◮ Generalized Linear Models. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Weighted Least Squares ◮ Suppose variances are known except for a constant factor. 2 2 ◮ That is, σi = σ /wi . ◮ Use weighted least squares. (See Chapter 10 in the text.) ◮ This usually arises realistically in the following situations: ◮ Yi is an average of ni measurements where you know ni . Then wi = ni . 2 ◮ Plots suggest that σi might be proportional to some power of 2 γ γ some covariate: σi = kxi . Then wi = xi− . Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Variances depending on (mean of) Y ◮ Two standard approaches are available: ◮ Older approach is transformation. ◮ Newer approach is use of generalized linear model; see STAT 402. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Transformation ◮ Compute Yi∗ = g(Yi ) for some function g like logarithm or square root. ◮ Then regress Yi∗ on the covariates. ◮ This approach sometimes works for skewed response variables like income; ◮ after transformation we occasionally find the errors are more nearly normal, more homoscedastic and that the model is simpler. ◮ See page 130ff and check under transformations and Box-Cox in the index. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Generalized Linear Models ◮ Transformation uses the model T E(g(Yi )) = xi β while generalized linear models use T g(E(Yi )) = xi β ◮ Generally latter approach offers more flexibility.
    [Show full text]
  • Section 1: Regression Review
    Section 1: Regression review Yotam Shem-Tov Fall 2015 Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 1 / 58 Contact information Yotam Shem-Tov, PhD student in economics. E-mail: [email protected]. Office: Evans hall room 650 Office hours: To be announced - any preferences or constraints? Feel free to e-mail me. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 2 / 58 R resources - Prior knowledge in R is assumed In the link here is an excellent introduction to statistics in R . There is a free online course in coursera on programming in R. Here is a link to the course. An excellent book for implementing econometric models and method in R is Applied Econometrics with R. This is my favourite for starting to learn R for someone who has some background in statistic methods in the social science. The book Regression Models for Data Science in R has a nice online version. It covers the implementation of regression models using R . A great link to R resources and other cool programming and econometric tools is here. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 3 / 58 Outline There are two general approaches to regression 1 Regression as a model: a data generating process (DGP) 2 Regression as an algorithm (i.e., an estimator without assuming an underlying structural model). Overview of this slides: 1 The conditional expectation function - a motivation for using OLS. 2 OLS as the minimum mean squared error linear approximation (projections). 3 Regression as a structural model (i.e., assuming the conditional expectation is linear).
    [Show full text]
  • Power Comparisons of the Mann-Whitney U and Permutation Tests
    Power Comparisons of the Mann-Whitney U and Permutation Tests Abstract: Though the Mann-Whitney U-test and permutation tests are often used in cases where distribution assumptions for the two-sample t-test for equal means are not met, it is not widely understood how the powers of the two tests compare. Our goal was to discover under what circumstances the Mann-Whitney test has greater power than the permutation test. The tests’ powers were compared under various conditions simulated from the Weibull distribution. Under most conditions, the permutation test provided greater power, especially with equal sample sizes and with unequal standard deviations. However, the Mann-Whitney test performed better with highly skewed data. Background and Significance: In many psychological, biological, and clinical trial settings, distributional differences among testing groups render parametric tests requiring normality, such as the z test and t test, unreliable. In these situations, nonparametric tests become necessary. Blair and Higgins (1980) illustrate the empirical invalidity of claims made in the mid-20th century that t and F tests used to detect differences in population means are highly insensitive to violations of distributional assumptions, and that non-parametric alternatives possess lower power. Through power testing, Blair and Higgins demonstrate that the Mann-Whitney test has much higher power relative to the t-test, particularly under small sample conditions. This seems to be true even when Welch’s approximation and pooled variances are used to “account” for violated t-test assumptions (Glass et al. 1972). With the proliferation of powerful computers, computationally intensive alternatives to the Mann-Whitney test have become possible.
    [Show full text]