DOCSLIB.ORG

Section 1: Regression Review

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Section 1: Regression Review Section 1: Regression review Yotam Shem-Tov Fall 2015 Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 1 / 58 Contact information Yotam Shem-Tov, PhD student in economics. E-mail: [email protected]. Office: Evans hall room 650 Office hours: To be announced - any preferences or constraints? Feel free to e-mail me. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 2 / 58 R resources - Prior knowledge in R is assumed In the link here is an excellent introduction to statistics in R . There is a free online course in coursera on programming in R. Here is a link to the course. An excellent book for implementing econometric models and method in R is Applied Econometrics with R. This is my favourite for starting to learn R for someone who has some background in statistic methods in the social science. The book Regression Models for Data Science in R has a nice online version. It covers the implementation of regression models using R . A great link to R resources and other cool programming and econometric tools is here. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 3 / 58 Outline There are two general approaches to regression 1 Regression as a model: a data generating process (DGP) 2 Regression as an algorithm (i.e., an estimator without assuming an underlying structural model). Overview of this slides: 1 The conditional expectation function - a motivation for using OLS. 2 OLS as the minimum mean squared error linear approximation (projections). 3 Regression as a structural model (i.e., assuming the conditional expectation is linear). 4 Applications, examples and additional topics. This slides relay heavily on Mostly Harmless Econometrics, Hansen's book Econometrics and Pat Kline's lecture notes. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 4 / 58 Notation and theoretical framework The researcher observes an i:i:d sample of N observations of (Yi ; Xi ), denoted by SN ≡ (Y1; X1);::: (YN ; XN ). 0 Xi = (X1i ; X2i ;:::; Xpi ) is a 1 × p random vector, where p is the number of covariates. Yi is a scalar random variable. (Yi ; Xi ) are sampled i:i:d from the distribution function FY ;X (y; x). Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 5 / 58 The Conditional expectations function (CEF) The conditional expectation function is, Z Z E[Yi jXi = x] = tdFY jX (tjXi = x) = tfY jX (tjXi = x)dt For any two variables Xi and Yi we can always compute the conditional expectation of one given the other. Additional assumptions are required to give anything other than a purely descriptive interpretation to the conditional expectation function. Descriptive tools are important and can be valuable. The law of iterated expectations (LIE) is, E[Yi ] = E [E [Yi jXi = x]] More in detail LIE is: EY [Yi ] = EX EY jX =x [Yi jXi = x] Another way of writing LIE is, E[Yi jX1i = x1] = E [E [Yi jX1i = x1; X2i = x2] jX1i = x1] Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 6 / 58 Properties of the CEF The LIE has several useful implications, E [Yi − E [Yi jXi ]] = 0 E [(Yi − E [Yi jXi ]) · Xi ] = 0 E [(Yi − E [Yi jXi ]) · g(Xi )] = 0 8 g(·) Therefore we can decompose any scalar random variable Yi to two parts, Yi = E [Yi jXi ] + ui ; E [ui jXi ] = 0: Question: Does E [ui jXi ]=0 implies E [ui ]=0? Yes, the proof follows from the LIE. The statement E [ui jXi ]=0 is more general than the statement E [ui ]=0. Question: Does E [ui ]=0 imply E [ui jXi ]=0? No. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 7 / 58 Properties of the CEF The ANOVA theorem (variance decomposition) V [Yi ] = V [E [Yi jXi ]] + E [V [Yi jXi ]] The CEF prediction property Let m(Xi ) be any function of Xi . The CEF solves, h 2i E [Yi jXi ] = argmin E (Yi − m(Xi )) m(Xi ) The CEF is the best predictor of Y using the loss function h i i ^ ^ 2 L(Yi ; Yi ) = E (Yi − Yi ) . The CEF is also refereed to as the minimum mean squares error (MMSE) estimator of Yi . Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 8 / 58 Homoskedasticity and Heteroskedasticity Homoskedasticity 2 2 The error is homoskedastic if E u jX = σ , does not depend on X . Hetroskedasticity 2 2 The error is hetroskedastic if E u jX = x = σ (x), depends on x. The concepts of homoskedasticity and heteroskedasticity concern the conditional variance, not the unconditional variance. By definition the unconditional variance σ2 is constant and independent of the regressors. The unconditional variance is a number, not a random variable or a function of X . The conditional variance depends on X and if X is a random variable it is also a random variable. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 9 / 58 Projections Denote the population linear projection of Yi on Xi by, p ∗ 0 X E [Yi jXi ] = Xi β = β0 + Xji βj j=1 where β is defined as the minimum mean squared error linear projection, h 0 2i β = argmin E Yi − Xi b b The F.O.C of the minimization problem are, 0 0−1 E Xi · Yi − Xi β = 0 ) β = E Xi Xi E [Xi Yi ] ∗ Denote by ei the projection residual, ei = Yi − E [Yi jXi ]. It follows from the F.O.C that, E [Xi · ei ] = 0. The residual of projecting Yi on Xi is not correlated with Xi . Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 10 / 58 Projections Theorem (Projection is the MMSE linear approximation to the CEF) h 0 2i β = argmin E E [Yi jXi ] − Xi b b 0 If the conditional expectation is linear, E [Yi jXi ] = Xi β then, ∗ E [Yi jXi ] = E [Yi jXi ]. Proof Projections and conditional expectations are related also without imposing any structural assumptions, ∗ ∗ E [Yi jXi ] = E [E [Yi jZi ; Xi ] jXi ] Proof: ∗ 0 0−1 0 0−1 E [Yi jXi ] = Xi E Xi Xi E [Xi Yi ] = Xi E Xi Xi E [Xi E [Yi jXi ; Zi ]] ∗ = E [E [Yi jZi ; Xi ] jXi ] 0 0 −1 ∗ where Xi E [Xi Xi ] E [Xi A] = E [AjXi ] for all A, and in our case A = E [Yi jZi ; Xi ]. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 11 / 58 Projections Projections also follow the law of iterated projections (LIP), ∗ ∗ ∗ E [Yi jXi ] = E [E [Yi jZi ; Xi ] jXi ] Consider the following special case, Ti is a binary variable (i.e., Ti 2 f0; 1g). Show that, ∗ E [Yi jTi ] = E [E [Yi jXi ; Ti ] jTi ] The proof is left as a homework assignment. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 12 / 58 Regression as a structural model: The CEF is linear 0 When E [Yi jXi ] = Xi β, β has a causal interpretation. It is no longer a linear approximation based on correlations, but a structural parameter that describes a relationship between Xi and Yi . The parameter β has two different possible interpretations: (i) Conditional mean interpretation: β indicates the effect of increasing X on the conditional mean E [Y jX ] in the model E [Y jX ] = X β. (ii) Unconditional mean interpretation: By the LIE it follows that E [Y ] = E [X ] β. Hence, β can be interpreted as the effect of increasing the mean value of X on the (unconditional) mean value of Y (i.e., E [Y ]). Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 13 / 58 Regression as a prediction algorithm Denote by X the design matrix. This is the matrix on which we will project y . In other words we have an input matrix X with dimensions n × p and an output vector y with dimensions n × 1. 0 1 X11 X12 ::: X1p B X21 X22 ::: X2p C X = B C B . C @ . A X X ::: X n1 n2 np n×p The Xji denotes the value of characteristic j for individual i. Example: If the researcher observes 2 covariates: education and age. A possible design matrix is, 0 2 1 1 education1 age1 agep B . C X = @ . A 1 education age age2 n n n n×4 Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 14 / 58 Regression as a prediction algorithm The linear regression algorithm has the following form: p X y^i = f (Xi ) = β0 + Xji βj j=1 We can estimate the coefficients β in a variety of ways but OLS is by far the most common, which minimizes the residual sum of squares (RSS): N P X X 2 RSS(β) = (yi − β0 − Xji βj ) i=1 j=1 The estimation of β is according to a square loss function, i.e. L(a; ^a) = (a − ^a)2. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 15 / 58 Visualization of OLS Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 16 / 58 The OLS estimator of β Write the RSS as: RSS(β) = (y − Xβ)0(y − xβ) Differentiate with respect to β: @RSS = −2X0(y − Xβ) (1) @β Assume that X is full rank (no perfect collinearity among any of the independent variables) and set first derivative to 0: X0(y − Xβ) = 0 Solve for β: β^ = (X0X)−1X0y Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 17 / 58 Rank condition for identifying β What happens if X is not full rank? There is an infinite number of ways to invert the matrix X0X, and the algorithm does not have a unique solution.
Load more

Recommended publications
  • Lecture 22: Bivariate Normal Distribution Distribution
    6.5 Conditional Distributions General Bivariate Normal Let Z1; Z2 ∼ N (0; 1), which we will use to build a general bivariate normal Lecture 22: Bivariate Normal Distribution distribution. 1 1 2 2 f (z1; z2) = exp − (z1 + z2 ) Statistics 104 2π 2 We want to transform these unit normal distributions to have the follow Colin Rundel arbitrary parameters: µX ; µY ; σX ; σY ; ρ April 11, 2012 X = σX Z1 + µX p 2 Y = σY [ρZ1 + 1 − ρ Z2] + µY Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 1 / 22 6.5 Conditional Distributions 6.5 Conditional Distributions General Bivariate Normal - Marginals General Bivariate Normal - Cov/Corr First, lets examine the marginal distributions of X and Y , Second, we can find Cov(X ; Y ) and ρ(X ; Y ) Cov(X ; Y ) = E [(X − E(X ))(Y − E(Y ))] X = σX Z1 + µX h p i = E (σ Z + µ − µ )(σ [ρZ + 1 − ρ2Z ] + µ − µ ) = σX N (0; 1) + µX X 1 X X Y 1 2 Y Y 2 h p 2 i = N (µX ; σX ) = E (σX Z1)(σY [ρZ1 + 1 − ρ Z2]) h 2 p 2 i = σX σY E ρZ1 + 1 − ρ Z1Z2 p 2 2 Y = σY [ρZ1 + 1 − ρ Z2] + µY = σX σY ρE[Z1 ] p 2 = σX σY ρ = σY [ρN (0; 1) + 1 − ρ N (0; 1)] + µY = σ [N (0; ρ2) + N (0; 1 − ρ2)] + µ Y Y Cov(X ; Y ) ρ(X ; Y ) = = ρ = σY N (0; 1) + µY σX σY 2 = N (µY ; σY ) Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 2 / 22 Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 3 / 22 6.5 Conditional Distributions 6.5 Conditional Distributions General Bivariate Normal - RNG Multivariate Change of Variables Consequently, if we want to generate a Bivariate Normal random variable Let X1;:::; Xn have a continuous joint distribution with pdf f defined of S.
    [Show full text]
  • Laws of Total Expectation and Total Variance
    Laws of Total Expectation and Total Variance Definition of conditional density. Assume and arbitrary random variable X with density fX . Take an event A with P (A) > 0. Then the conditional density fXjA is defined as follows: 8 < f(x) 2 P (A) x A fXjA(x) = : 0 x2 = A Note that the support of fXjA is supported only in A. Definition of conditional expectation conditioned on an event. Z Z 1 E(h(X)jA) = h(x) fXjA(x) dx = h(x) fX (x) dx A P (A) A Example. For the random variable X with density function 8 < 1 3 64 x 0 < x < 4 f(x) = : 0 otherwise calculate E(X2 j X ≥ 1). Solution. Step 1. Z h i 4 1 1 1 x=4 255 P (X ≥ 1) = x3 dx = x4 = 1 64 256 4 x=1 256 Step 2. Z Z ( ) 1 256 4 1 E(X2 j X ≥ 1) = x2 f(x) dx = x2 x3 dx P (X ≥ 1) fx≥1g 255 1 64 Z ( ) ( )( ) h i 256 4 1 256 1 1 x=4 8192 = x5 dx = x6 = 255 1 64 255 64 6 x=1 765 Definition of conditional variance conditioned on an event. Var(XjA) = E(X2jA) − E(XjA)2 1 Example. For the previous example , calculate the conditional variance Var(XjX ≥ 1) Solution. We already calculated E(X2 j X ≥ 1). We only need to calculate E(X j X ≥ 1). Z Z Z ( ) 1 256 4 1 E(X j X ≥ 1) = x f(x) dx = x x3 dx P (X ≥ 1) fx≥1g 255 1 64 Z ( ) ( )( ) h i 256 4 1 256 1 1 x=4 4096 = x4 dx = x5 = 255 1 64 255 64 5 x=1 1275 Finally: ( ) 8192 4096 2 630784 Var(XjX ≥ 1) = E(X2jX ≥ 1) − E(XjX ≥ 1)2 = − = 765 1275 1625625 Definition of conditional expectation conditioned on a random variable.
    [Show full text]
  • Multicollinearity
    Chapter 10 Multicollinearity 10.1 The Nature of Multicollinearity 10.1.1 Extreme Collinearity The standard OLS assumption that ( xi1; xi2; : : : ; xik ) not be linearly related means that for any ( c1; c2; : : : ; ck ) xik =6 c1xi1 + c2xi2 + ··· + ck 1xi;k 1 (10.1) − − for some i. If the assumption is violated, then we can find ( c1; c2; : : : ; ck 1 ) such that − xik = c1xi1 + c2xi2 + ··· + ck 1xi;k 1 (10.2) − − for all i. Define x12 ··· x1k xk1 c1 x22 ··· x2k xk2 c2 X1 = 0 . 1 ; xk = 0 . 1 ; and c = 0 . 1 : . B C B C B C B xn2 ··· xnk C B xkn C B ck 1 C B C B C B − C @ A @ A @ A Then extreme collinearity can be represented as xk = X1c: (10.3) We have represented extreme collinearity in terms of the last explanatory vari- able. Since we can always re-order the variables this choice is without loss of generality and the analysis could be applied to any non-constant variable by moving it to the last column. 10.1.2 Near Extreme Collinearity Of course, it is rare, in practice, that an exact linear relationship holds. Instead, we have xik = c1xi1 + c2xi2 + ··· + ck 1xi;k 1 + vi (10.4) − − 133 134 CHAPTER 10. MULTICOLLINEARITY or, more compactly, xk = X1c + v; (10.5) where the v's are small relative to the x's. If we think of the v's as random variables they will have small variance (and zero mean if X includes a column of ones). A convenient way to algebraically express the degree of collinearity is the sample correlation between xik and wi = c1xi1 +c2xi2 +···+ck 1xi;k 1, namely − − cov( xik; wi ) cov( wi + vi; wi ) rx;w = = (10.6) var(xi;k)var(wi) var(wi + vi)var(wi) d d Clearly, as the variancep of vi grows small, thisp value will go to unity.
    [Show full text]
  • CONDITIONAL EXPECTATION Definition 1. Let (Ω,F,P)
    CONDITIONAL EXPECTATION 1. CONDITIONAL EXPECTATION: L2 THEORY ¡ Definition 1. Let (­,F ,P) be a probability space and let G be a σ algebra contained in F . For ¡ any real random variable X L2(­,F ,P), define E(X G ) to be the orthogonal projection of X 2 j onto the closed subspace L2(­,G ,P). This definition may seem a bit strange at first, as it seems not to have any connection with the naive definition of conditional probability that you may have learned in elementary prob- ability. However, there is a compelling rationale for Definition 1: the orthogonal projection E(X G ) minimizes the expected squared difference E(X Y )2 among all random variables Y j ¡ 2 L2(­,G ,P), so in a sense it is the best predictor of X based on the information in G . It may be helpful to consider the special case where the σ algebra G is generated by a single random ¡ variable Y , i.e., G σ(Y ). In this case, every G measurable random variable is a Borel function Æ ¡ of Y (exercise!), so E(X G ) is the unique Borel function h(Y ) (up to sets of probability zero) that j minimizes E(X h(Y ))2. The following exercise indicates that the special case where G σ(Y ) ¡ Æ for some real-valued random variable Y is in fact very general. Exercise 1. Show that if G is countably generated (that is, there is some countable collection of set B G such that G is the smallest σ algebra containing all of the sets B ) then there is a j 2 ¡ j G measurable real random variable Y such that G σ(Y ).
    [Show full text]
  • Conditional Expectation and Prediction Conditional Frequency Functions and Pdfs Have Properties of Ordinary Frequency and Density Functions
    Conditional expectation and prediction Conditional frequency functions and pdfs have properties of ordinary frequency and density functions. Hence, associated with a conditional distribution is a conditional mean. Y and X are discrete random variables, the conditional frequency function of Y given x is pY|X(y|x). Conditional expectation of Y given X=x is Continuous case: Conditional expectation of a function: Consider a Poisson process on [0, 1] with mean λ, and let N be the # of points in [0, 1]. For p < 1, let X be the number of points in [0, p]. Find the conditional distribution and conditional mean of X given N = n. Make a guess! Consider a Poisson process on [0, 1] with mean λ, and let N be the # of points in [0, 1]. For p < 1, let X be the number of points in [0, p]. Find the conditional distribution and conditional mean of X given N = n. We first find the joint distribution: P(X = x, N = n), which is the probability of x events in [0, p] and n−x events in [p, 1]. From the assumption of a Poisson process, the counts in the two intervals are independent Poisson random variables with parameters pλ and (1−p)λ (why?), so N has Poisson marginal distribution, so the conditional frequency function of X is Binomial distribution, Conditional expectation is np. Conditional expectation of Y given X=x is a function of X, and hence also a random variable, E(Y|X). In the last example, E(X|N=n)=np, and E(X|N)=Np is a function of N, a random variable that generally has an expectation Taken w.r.t.
    [Show full text]
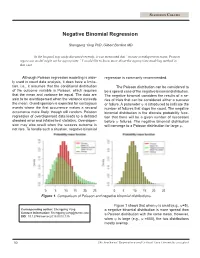
  • Negative Binomial Regression
    STATISTICS COLUMN Negative Binomial Regression Shengping Yang PhD ,Gilbert Berdine MD In the hospital stay study discussed recently, it was mentioned that “in case overdispersion exists, Poisson regression model might not be appropriate.” I would like to know more about the appropriate modeling method in that case. Although Poisson regression modeling is wide- regression is commonly recommended. ly used in count data analysis, it does have a limita- tion, i.e., it assumes that the conditional distribution The Poisson distribution can be considered to of the outcome variable is Poisson, which requires be a special case of the negative binomial distribution. that the mean and variance be equal. The data are The negative binomial considers the results of a se- said to be overdispersed when the variance exceeds ries of trials that can be considered either a success the mean. Overdispersion is expected for contagious or failure. A parameter ψ is introduced to indicate the events where the first occurrence makes a second number of failures that stops the count. The negative occurrence more likely, though still random. Poisson binomial distribution is the discrete probability func- regression of overdispersed data leads to a deflated tion that there will be a given number of successes standard error and inflated test statistics. Overdisper- before ψ failures. The negative binomial distribution sion may also result when the success outcome is will converge to a Poisson distribution for large ψ. not rare. To handle such a situation, negative binomial 0 5 10 15 20 25 0 5 10 15 20 25 Figure 1. Comparison of Poisson and negative binomial distributions.
    [Show full text]
  • Assumptions of the Simple Classical Linear Regression Model (CLRM)
    ECONOMICS 351* -- NOTE 1 M.G. Abbott ECON 351* -- NOTE 1 Specification -- Assumptions of the Simple Classical Linear Regression Model (CLRM) 1. Introduction CLRM stands for the Classical Linear Regression Model. The CLRM is also known as the standard linear regression model. Three sets of assumptions define the CLRM. 1. Assumptions respecting the formulation of the population regression equation, or PRE. Assumption A1 2. Assumptions respecting the statistical properties of the random error term and the dependent variable. Assumptions A2-A4 3. Assumptions respecting the properties of the sample data. Assumptions A5-A8 ECON 351* -- Note 1: Specification of the Simple CLRM … Page 1 of 16 pages ECONOMICS 351* -- NOTE 1 M.G. Abbott • Figure 2.1 Plot of Population Data Points, Conditional Means E(Y|X), and the Population Regression Function PRF Y Fitted values 200 $ PRF = 175 e, ur β0 + β1Xi t i nd 150 pe ex n o i t 125 p um 100 cons y ekl e W 75 50 60 80 100 120 140 160 180 200 220 240 260 Weekly income, $ Recall that the solid line in Figure 2.1 is the population regression function, which takes the form f (Xi ) = E(Yi Xi ) = β0 + β1Xi . For each population value Xi of X, there is a conditional distribution of population Y values and a corresponding conditional distribution of population random errors u, where (1) each population value of u for X = Xi is u i X i = Yi − E(Yi X i ) = Yi − β0 − β1 X i , and (2) each population value of Y for X = Xi is Yi X i = E(Yi X i ) + u i = β0 + β1 X i + u i .
    [Show full text]
  • Lectures Prepared By: Elchanan Mossel Yelena Shvets
    Introduction to probability Stat 134 FAll 2005 Berkeley Lectures prepared by: Elchanan Mossel Yelena Shvets Follows Jim Pitman’s book: Probability Sections 6.1-6.2 # of Heads in a Random # of Tosses •Suppose a fair die is rolled and let N be the number on top. N=5 •Next a fair coin is tossed N times and H, the number of heads is recorded: H=3 Question : Find the distribution of H, the number of heads? # of Heads in a Random Number of Tosses Solution : •The conditional probability for the H=h , given N=n is •By the rule of the average conditional probability and using P(N=n) = 1/6 h 0 1 2 3 4 5 6 P(H=h) 63/384 120/384 99/384 64/384 29/384 8/384 1/384 Conditional Distribution of Y given X =x Def: For each value x of X, the set of probabilities P(Y=y|X=x) where y varies over all possible values of Y, form a probability distribution, depending on x, called the conditional distribution of Y given X=x . Remarks: •In the example P(H = h | N =n) ~ binomial(n,½). •The unconditional distribution of Y is the average of the conditional distributions, weighted by P(X=x). Conditional Distribution of X given Y=y Remark: Once we have the conditional distribution of Y given X=x , using Bayes’ rule we may obtain the conditional distribution of X given Y=y . •Example : We have computed distribution of H given N = n : •Using the product rule we can get the joint distr.
    [Show full text]
  • (Introduction to Probability at an Advanced Level) - All Lecture Notes
    Fall 2018 Statistics 201A (Introduction to Probability at an advanced level) - All Lecture Notes Aditya Guntuboyina August 15, 2020 Contents 0.1 Sample spaces, Events, Probability.................................5 0.2 Conditional Probability and Independence.............................6 0.3 Random Variables..........................................7 1 Random Variables, Expectation and Variance8 1.1 Expectations of Random Variables.................................9 1.2 Variance................................................ 10 2 Independence of Random Variables 11 3 Common Distributions 11 3.1 Ber(p) Distribution......................................... 11 3.2 Bin(n; p) Distribution........................................ 11 3.3 Poisson Distribution......................................... 12 4 Covariance, Correlation and Regression 14 5 Correlation and Regression 16 6 Back to Common Distributions 16 6.1 Geometric Distribution........................................ 16 6.2 Negative Binomial Distribution................................... 17 7 Continuous Distributions 17 7.1 Normal or Gaussian Distribution.................................. 17 1 7.2 Uniform Distribution......................................... 18 7.3 The Exponential Density...................................... 18 7.4 The Gamma Density......................................... 18 8 Variable Transformations 19 9 Distribution Functions and the Quantile Transform 20 10 Joint Densities 22 11 Joint Densities under Transformations 23 11.1 Detour to Convolutions......................................
    [Show full text]
  • 5. Conditional Expectation A. Definition of Conditional Expectation
    5. Conditional Expectation A. Definition of conditional expectation Suppose that we have partial information about the outcome ω, drawn from Ω according to probability measure IP ; the partial information might be in the form of the value of a random vector Y (ω)orofaneventB in which ω is known to lie. The concept of conditional expectation tells us how to calculate the expected values and probabilities using this information. The general definition of conditional expectation is fairly abstract and takes a bit of getting used to. We shall first build intuition by recalling the definitions of conditional expectaion in elementary elementary probability theory, and showing how they can be used to compute certain Radon-Nikodym derivatives. With this as motivation, we then develop the fully general definition. Before doing any prob- ability, though, we pause to review the Radon-Nikodym theorem, which plays an essential role in the theory. The Radon-Nikodym theorem. Let ν be a positive measure on a measurable space (S, S). If µ is a signed measure on (S, S), µ is said to be absolutely continuous with respect to ν, written µ ν,if µ(A) = 0 whenever ν(A)=0. SupposeZ that f is a ν-integrable function on (S, S) and define the new measure µ(A)= f(s)ν(ds), A ∈S. Then, clearly, µ ν. The Radon-Nikodym theorem A says that all measures which are absolutely continuous to ν arise in this way. Theorem (Radon-Nikodym). Let ν be a σ-finite, positive measure on (SsS). (This means that there is a countable covering A1,A2,..
    [Show full text]
  • Week 6: Linear Regression with Two Regressors
    Week 6: Linear Regression with Two Regressors Brandon Stewart1 Princeton October 17, 19, 2016 1These slides are heavily influenced by Matt Blackwell, Adam Glynn and Jens Hainmueller. Stewart (Princeton) Week 6: Two Regressors October 17, 19, 2016 1 / 132 Where We've Been and Where We're Going... Last Week I mechanics of OLS with one variable I properties of OLS This Week I Monday: F adding a second variable F new mechanics I Wednesday: F omitted variable bias F multicollinearity F interactions Next Week I multiple regression Long Run I probability inference regression ! ! Questions? Stewart (Princeton) Week 6: Two Regressors October 17, 19, 2016 2 / 132 1 Two Examples 2 Adding a Binary Variable 3 Adding a Continuous Covariate 4 Once More With Feeling 5 OLS Mechanics and Partialing Out 6 Fun With Red and Blue 7 Omitted Variables 8 Multicollinearity 9 Dummy Variables 10 Interaction Terms 11 Polynomials 12 Conclusion 13 Fun With Interactions Stewart (Princeton) Week 6: Two Regressors October 17, 19, 2016 3 / 132 Why Do We Want More Than One Predictor? Summarize more information for descriptive inference Improve the fit and predictive power of our model Control for confounding factors for causal inference 2 Model non-linearities (e.g. Y = β0 + β1X + β2X ) Model interactive effects (e.g. Y = β0 + β1X + β2X2 + β3X1X2) Stewart (Princeton) Week 6: Two Regressors October 17, 19, 2016 4 / 132 Example 1: Cigarette Smokers and Pipe Smokers Stewart (Princeton) Week 6: Two Regressors October 17, 19, 2016 5 / 132 Example 1: Cigarette Smokers and Pipe Smokers Consider the following example from Cochran (1968).
    [Show full text]
  • CONDITIONAL EXPECTATION Definition 1. Let (Ω,F,P) Be A
    CONDITIONAL EXPECTATION STEVEN P.LALLEY 1. CONDITIONAL EXPECTATION: L2 THEORY ¡ Definition 1. Let (­,F ,P) be a probability space and let G be a σ algebra contained in F . For ¡ any real random variable X L2(­,F ,P), define E(X G ) to be the orthogonal projection of X 2 j onto the closed subspace L2(­,G ,P). This definition may seem a bit strange at first, as it seems not to have any connection with the naive definition of conditional probability that you may have learned in elementary prob- ability. However, there is a compelling rationale for Definition 1: the orthogonal projection E(X G ) minimizes the expected squared difference E(X Y )2 among all random variables Y j ¡ 2 L2(­,G ,P), so in a sense it is the best predictor of X based on the information in G . It may be helpful to consider the special case where the σ algebra G is generated by a single random ¡ variable Y , i.e., G σ(Y ). In this case, every G measurable random variable is a Borel function Æ ¡ of Y (exercise!), so E(X G ) is the unique Borel function h(Y ) (up to sets of probability zero) that j minimizes E(X h(Y ))2. The following exercise indicates that the special case where G σ(Y ) ¡ Æ for some real-valued random variable Y is in fact very general. Exercise 1. Show that if G is countably generated (that is, there is some countable collection of set B G such that G is the smallest σ algebra containing all of the sets B ) then there is a j 2 ¡ j G measurable real random variable Y such that G σ(Y ).
    [Show full text]