Week 6: Linear Regression with Two Regressors
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lecture 22: Bivariate Normal Distribution Distribution
6.5 Conditional Distributions General Bivariate Normal Let Z1; Z2 ∼ N (0; 1), which we will use to build a general bivariate normal Lecture 22: Bivariate Normal Distribution distribution. 1 1 2 2 f (z1; z2) = exp − (z1 + z2 ) Statistics 104 2π 2 We want to transform these unit normal distributions to have the follow Colin Rundel arbitrary parameters: µX ; µY ; σX ; σY ; ρ April 11, 2012 X = σX Z1 + µX p 2 Y = σY [ρZ1 + 1 − ρ Z2] + µY Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 1 / 22 6.5 Conditional Distributions 6.5 Conditional Distributions General Bivariate Normal - Marginals General Bivariate Normal - Cov/Corr First, lets examine the marginal distributions of X and Y , Second, we can find Cov(X ; Y ) and ρ(X ; Y ) Cov(X ; Y ) = E [(X − E(X ))(Y − E(Y ))] X = σX Z1 + µX h p i = E (σ Z + µ − µ )(σ [ρZ + 1 − ρ2Z ] + µ − µ ) = σX N (0; 1) + µX X 1 X X Y 1 2 Y Y 2 h p 2 i = N (µX ; σX ) = E (σX Z1)(σY [ρZ1 + 1 − ρ Z2]) h 2 p 2 i = σX σY E ρZ1 + 1 − ρ Z1Z2 p 2 2 Y = σY [ρZ1 + 1 − ρ Z2] + µY = σX σY ρE[Z1 ] p 2 = σX σY ρ = σY [ρN (0; 1) + 1 − ρ N (0; 1)] + µY = σ [N (0; ρ2) + N (0; 1 − ρ2)] + µ Y Y Cov(X ; Y ) ρ(X ; Y ) = = ρ = σY N (0; 1) + µY σX σY 2 = N (µY ; σY ) Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 2 / 22 Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 3 / 22 6.5 Conditional Distributions 6.5 Conditional Distributions General Bivariate Normal - RNG Multivariate Change of Variables Consequently, if we want to generate a Bivariate Normal random variable Let X1;:::; Xn have a continuous joint distribution with pdf f defined of S. -
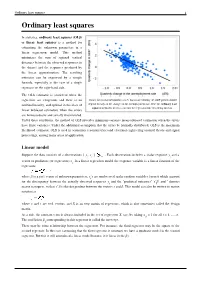
Ordinary Least Squares 1 Ordinary Least Squares
Ordinary least squares 1 Ordinary least squares In statistics, ordinary least squares (OLS) or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear approximation. The resulting estimator can be expressed by a simple formula, especially in the case of a single regressor on the right-hand side. The OLS estimator is consistent when the regressors are exogenous and there is no Okun's law in macroeconomics states that in an economy the GDP growth should multicollinearity, and optimal in the class of depend linearly on the changes in the unemployment rate. Here the ordinary least squares method is used to construct the regression line describing this law. linear unbiased estimators when the errors are homoscedastic and serially uncorrelated. Under these conditions, the method of OLS provides minimum-variance mean-unbiased estimation when the errors have finite variances. Under the additional assumption that the errors be normally distributed, OLS is the maximum likelihood estimator. OLS is used in economics (econometrics) and electrical engineering (control theory and signal processing), among many areas of application. Linear model Suppose the data consists of n observations { y , x } . Each observation includes a scalar response y and a i i i vector of predictors (or regressors) x . In a linear regression model the response variable is a linear function of the i regressors: where β is a p×1 vector of unknown parameters; ε 's are unobserved scalar random variables (errors) which account i for the discrepancy between the actually observed responses y and the "predicted outcomes" x′ β; and ′ denotes i i matrix transpose, so that x′ β is the dot product between the vectors x and β. -

Laws of Total Expectation and Total Variance
Laws of Total Expectation and Total Variance Definition of conditional density. Assume and arbitrary random variable X with density fX . Take an event A with P (A) > 0. Then the conditional density fXjA is defined as follows: 8 < f(x) 2 P (A) x A fXjA(x) = : 0 x2 = A Note that the support of fXjA is supported only in A. Definition of conditional expectation conditioned on an event. Z Z 1 E(h(X)jA) = h(x) fXjA(x) dx = h(x) fX (x) dx A P (A) A Example. For the random variable X with density function 8 < 1 3 64 x 0 < x < 4 f(x) = : 0 otherwise calculate E(X2 j X ≥ 1). Solution. Step 1. Z h i 4 1 1 1 x=4 255 P (X ≥ 1) = x3 dx = x4 = 1 64 256 4 x=1 256 Step 2. Z Z ( ) 1 256 4 1 E(X2 j X ≥ 1) = x2 f(x) dx = x2 x3 dx P (X ≥ 1) fx≥1g 255 1 64 Z ( ) ( )( ) h i 256 4 1 256 1 1 x=4 8192 = x5 dx = x6 = 255 1 64 255 64 6 x=1 765 Definition of conditional variance conditioned on an event. Var(XjA) = E(X2jA) − E(XjA)2 1 Example. For the previous example , calculate the conditional variance Var(XjX ≥ 1) Solution. We already calculated E(X2 j X ≥ 1). We only need to calculate E(X j X ≥ 1). Z Z Z ( ) 1 256 4 1 E(X j X ≥ 1) = x f(x) dx = x x3 dx P (X ≥ 1) fx≥1g 255 1 64 Z ( ) ( )( ) h i 256 4 1 256 1 1 x=4 4096 = x4 dx = x5 = 255 1 64 255 64 5 x=1 1275 Finally: ( ) 8192 4096 2 630784 Var(XjX ≥ 1) = E(X2jX ≥ 1) − E(XjX ≥ 1)2 = − = 765 1275 1625625 Definition of conditional expectation conditioned on a random variable. -

Multicollinearity
Chapter 10 Multicollinearity 10.1 The Nature of Multicollinearity 10.1.1 Extreme Collinearity The standard OLS assumption that ( xi1; xi2; : : : ; xik ) not be linearly related means that for any ( c1; c2; : : : ; ck ) xik =6 c1xi1 + c2xi2 + ··· + ck 1xi;k 1 (10.1) − − for some i. If the assumption is violated, then we can find ( c1; c2; : : : ; ck 1 ) such that − xik = c1xi1 + c2xi2 + ··· + ck 1xi;k 1 (10.2) − − for all i. Define x12 ··· x1k xk1 c1 x22 ··· x2k xk2 c2 X1 = 0 . 1 ; xk = 0 . 1 ; and c = 0 . 1 : . B C B C B C B xn2 ··· xnk C B xkn C B ck 1 C B C B C B − C @ A @ A @ A Then extreme collinearity can be represented as xk = X1c: (10.3) We have represented extreme collinearity in terms of the last explanatory vari- able. Since we can always re-order the variables this choice is without loss of generality and the analysis could be applied to any non-constant variable by moving it to the last column. 10.1.2 Near Extreme Collinearity Of course, it is rare, in practice, that an exact linear relationship holds. Instead, we have xik = c1xi1 + c2xi2 + ··· + ck 1xi;k 1 + vi (10.4) − − 133 134 CHAPTER 10. MULTICOLLINEARITY or, more compactly, xk = X1c + v; (10.5) where the v's are small relative to the x's. If we think of the v's as random variables they will have small variance (and zero mean if X includes a column of ones). A convenient way to algebraically express the degree of collinearity is the sample correlation between xik and wi = c1xi1 +c2xi2 +···+ck 1xi;k 1, namely − − cov( xik; wi ) cov( wi + vi; wi ) rx;w = = (10.6) var(xi;k)var(wi) var(wi + vi)var(wi) d d Clearly, as the variancep of vi grows small, thisp value will go to unity. -

CONDITIONAL EXPECTATION Definition 1. Let (Ω,F,P)
CONDITIONAL EXPECTATION 1. CONDITIONAL EXPECTATION: L2 THEORY ¡ Definition 1. Let (,F ,P) be a probability space and let G be a σ algebra contained in F . For ¡ any real random variable X L2(,F ,P), define E(X G ) to be the orthogonal projection of X 2 j onto the closed subspace L2(,G ,P). This definition may seem a bit strange at first, as it seems not to have any connection with the naive definition of conditional probability that you may have learned in elementary prob- ability. However, there is a compelling rationale for Definition 1: the orthogonal projection E(X G ) minimizes the expected squared difference E(X Y )2 among all random variables Y j ¡ 2 L2(,G ,P), so in a sense it is the best predictor of X based on the information in G . It may be helpful to consider the special case where the σ algebra G is generated by a single random ¡ variable Y , i.e., G σ(Y ). In this case, every G measurable random variable is a Borel function Æ ¡ of Y (exercise!), so E(X G ) is the unique Borel function h(Y ) (up to sets of probability zero) that j minimizes E(X h(Y ))2. The following exercise indicates that the special case where G σ(Y ) ¡ Æ for some real-valued random variable Y is in fact very general. Exercise 1. Show that if G is countably generated (that is, there is some countable collection of set B G such that G is the smallest σ algebra containing all of the sets B ) then there is a j 2 ¡ j G measurable real random variable Y such that G σ(Y ). -

Conditional Expectation and Prediction Conditional Frequency Functions and Pdfs Have Properties of Ordinary Frequency and Density Functions
Conditional expectation and prediction Conditional frequency functions and pdfs have properties of ordinary frequency and density functions. Hence, associated with a conditional distribution is a conditional mean. Y and X are discrete random variables, the conditional frequency function of Y given x is pY|X(y|x). Conditional expectation of Y given X=x is Continuous case: Conditional expectation of a function: Consider a Poisson process on [0, 1] with mean λ, and let N be the # of points in [0, 1]. For p < 1, let X be the number of points in [0, p]. Find the conditional distribution and conditional mean of X given N = n. Make a guess! Consider a Poisson process on [0, 1] with mean λ, and let N be the # of points in [0, 1]. For p < 1, let X be the number of points in [0, p]. Find the conditional distribution and conditional mean of X given N = n. We first find the joint distribution: P(X = x, N = n), which is the probability of x events in [0, p] and n−x events in [p, 1]. From the assumption of a Poisson process, the counts in the two intervals are independent Poisson random variables with parameters pλ and (1−p)λ (why?), so N has Poisson marginal distribution, so the conditional frequency function of X is Binomial distribution, Conditional expectation is np. Conditional expectation of Y given X=x is a function of X, and hence also a random variable, E(Y|X). In the last example, E(X|N=n)=np, and E(X|N)=Np is a function of N, a random variable that generally has an expectation Taken w.r.t. -

Section 1: Regression Review
Section 1: Regression review Yotam Shem-Tov Fall 2015 Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 1 / 58 Contact information Yotam Shem-Tov, PhD student in economics. E-mail: [email protected]. Office: Evans hall room 650 Office hours: To be announced - any preferences or constraints? Feel free to e-mail me. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 2 / 58 R resources - Prior knowledge in R is assumed In the link here is an excellent introduction to statistics in R . There is a free online course in coursera on programming in R. Here is a link to the course. An excellent book for implementing econometric models and method in R is Applied Econometrics with R. This is my favourite for starting to learn R for someone who has some background in statistic methods in the social science. The book Regression Models for Data Science in R has a nice online version. It covers the implementation of regression models using R . A great link to R resources and other cool programming and econometric tools is here. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 3 / 58 Outline There are two general approaches to regression 1 Regression as a model: a data generating process (DGP) 2 Regression as an algorithm (i.e., an estimator without assuming an underlying structural model). Overview of this slides: 1 The conditional expectation function - a motivation for using OLS. 2 OLS as the minimum mean squared error linear approximation (projections). 3 Regression as a structural model (i.e., assuming the conditional expectation is linear). -

Assumptions of the Simple Classical Linear Regression Model (CLRM)
ECONOMICS 351* -- NOTE 1 M.G. Abbott ECON 351* -- NOTE 1 Specification -- Assumptions of the Simple Classical Linear Regression Model (CLRM) 1. Introduction CLRM stands for the Classical Linear Regression Model. The CLRM is also known as the standard linear regression model. Three sets of assumptions define the CLRM. 1. Assumptions respecting the formulation of the population regression equation, or PRE. Assumption A1 2. Assumptions respecting the statistical properties of the random error term and the dependent variable. Assumptions A2-A4 3. Assumptions respecting the properties of the sample data. Assumptions A5-A8 ECON 351* -- Note 1: Specification of the Simple CLRM … Page 1 of 16 pages ECONOMICS 351* -- NOTE 1 M.G. Abbott • Figure 2.1 Plot of Population Data Points, Conditional Means E(Y|X), and the Population Regression Function PRF Y Fitted values 200 $ PRF = 175 e, ur β0 + β1Xi t i nd 150 pe ex n o i t 125 p um 100 cons y ekl e W 75 50 60 80 100 120 140 160 180 200 220 240 260 Weekly income, $ Recall that the solid line in Figure 2.1 is the population regression function, which takes the form f (Xi ) = E(Yi Xi ) = β0 + β1Xi . For each population value Xi of X, there is a conditional distribution of population Y values and a corresponding conditional distribution of population random errors u, where (1) each population value of u for X = Xi is u i X i = Yi − E(Yi X i ) = Yi − β0 − β1 X i , and (2) each population value of Y for X = Xi is Yi X i = E(Yi X i ) + u i = β0 + β1 X i + u i . -

Lectures Prepared By: Elchanan Mossel Yelena Shvets
Introduction to probability Stat 134 FAll 2005 Berkeley Lectures prepared by: Elchanan Mossel Yelena Shvets Follows Jim Pitman’s book: Probability Sections 6.1-6.2 # of Heads in a Random # of Tosses •Suppose a fair die is rolled and let N be the number on top. N=5 •Next a fair coin is tossed N times and H, the number of heads is recorded: H=3 Question : Find the distribution of H, the number of heads? # of Heads in a Random Number of Tosses Solution : •The conditional probability for the H=h , given N=n is •By the rule of the average conditional probability and using P(N=n) = 1/6 h 0 1 2 3 4 5 6 P(H=h) 63/384 120/384 99/384 64/384 29/384 8/384 1/384 Conditional Distribution of Y given X =x Def: For each value x of X, the set of probabilities P(Y=y|X=x) where y varies over all possible values of Y, form a probability distribution, depending on x, called the conditional distribution of Y given X=x . Remarks: •In the example P(H = h | N =n) ~ binomial(n,½). •The unconditional distribution of Y is the average of the conditional distributions, weighted by P(X=x). Conditional Distribution of X given Y=y Remark: Once we have the conditional distribution of Y given X=x , using Bayes’ rule we may obtain the conditional distribution of X given Y=y . •Example : We have computed distribution of H given N = n : •Using the product rule we can get the joint distr. -

An Analysis of Random Design Linear Regression
An Analysis of Random Design Linear Regression Daniel Hsu1,2, Sham M. Kakade2, and Tong Zhang1 1Department of Statistics, Rutgers University 2Department of Statistics, Wharton School, University of Pennsylvania Abstract The random design setting for linear regression concerns estimators based on a random sam- ple of covariate/response pairs. This work gives explicit bounds on the prediction error for the ordinary least squares estimator and the ridge regression estimator under mild assumptions on the covariate/response distributions. In particular, this work provides sharp results on the \out-of-sample" prediction error, as opposed to the \in-sample" (fixed design) error. Our anal- ysis also explicitly reveals the effect of noise vs. modeling errors. The approach reveals a close connection to the more traditional fixed design setting, and our methods make use of recent ad- vances in concentration inequalities (for vectors and matrices). We also describe an application of our results to fast least squares computations. 1 Introduction In the random design setting for linear regression, one is given pairs (X1;Y1);:::; (Xn;Yn) of co- variates and responses, sampled from a population, where each Xi are random vectors and Yi 2 R. These pairs are hypothesized to have the linear relationship > Yi = Xi β + i for some linear map β, where the i are noise terms. The goal of estimation in this setting is to find coefficients β^ based on these (Xi;Yi) pairs such that the expected prediction error on a new > 2 draw (X; Y ) from the population, measured as E[(X β^ − Y ) ], is as small as possible. -

5. Conditional Expectation A. Definition of Conditional Expectation
5. Conditional Expectation A. Definition of conditional expectation Suppose that we have partial information about the outcome ω, drawn from Ω according to probability measure IP ; the partial information might be in the form of the value of a random vector Y (ω)orofaneventB in which ω is known to lie. The concept of conditional expectation tells us how to calculate the expected values and probabilities using this information. The general definition of conditional expectation is fairly abstract and takes a bit of getting used to. We shall first build intuition by recalling the definitions of conditional expectaion in elementary elementary probability theory, and showing how they can be used to compute certain Radon-Nikodym derivatives. With this as motivation, we then develop the fully general definition. Before doing any prob- ability, though, we pause to review the Radon-Nikodym theorem, which plays an essential role in the theory. The Radon-Nikodym theorem. Let ν be a positive measure on a measurable space (S, S). If µ is a signed measure on (S, S), µ is said to be absolutely continuous with respect to ν, written µ ν,if µ(A) = 0 whenever ν(A)=0. SupposeZ that f is a ν-integrable function on (S, S) and define the new measure µ(A)= f(s)ν(ds), A ∈S. Then, clearly, µ ν. The Radon-Nikodym theorem A says that all measures which are absolutely continuous to ν arise in this way. Theorem (Radon-Nikodym). Let ν be a σ-finite, positive measure on (SsS). (This means that there is a countable covering A1,A2,.. -
![ROBUST LINEAR LEAST SQUARES REGRESSION 3 Bias Term R(F ∗) R(F (Reg)) Has the Order D/N of the Estimation Term (See [3, 6, 10] and References− Within)](https://docslib.b-cdn.net/cover/5087/robust-linear-least-squares-regression-3-bias-term-r-f-r-f-reg-has-the-order-d-n-of-the-estimation-term-see-3-6-10-and-references-within-1085087.webp)
ROBUST LINEAR LEAST SQUARES REGRESSION 3 Bias Term R(F ∗) R(F (Reg)) Has the Order D/N of the Estimation Term (See [3, 6, 10] and References− Within)
The Annals of Statistics 2011, Vol. 39, No. 5, 2766–2794 DOI: 10.1214/11-AOS918 c Institute of Mathematical Statistics, 2011 ROBUST LINEAR LEAST SQUARES REGRESSION By Jean-Yves Audibert and Olivier Catoni Universit´eParis-Est and CNRS/Ecole´ Normale Sup´erieure/INRIA and CNRS/Ecole´ Normale Sup´erieure and INRIA We consider the problem of robustly predicting as well as the best linear combination of d given functions in least squares regres- sion, and variants of this problem including constraints on the pa- rameters of the linear combination. For the ridge estimator and the ordinary least squares estimator, and their variants, we provide new risk bounds of order d/n without logarithmic factor unlike some stan- dard results, where n is the size of the training data. We also provide a new estimator with better deviations in the presence of heavy-tailed noise. It is based on truncating differences of losses in a min–max framework and satisfies a d/n risk bound both in expectation and in deviations. The key common surprising factor of these results is the absence of exponential moment condition on the output distribution while achieving exponential deviations. All risk bounds are obtained through a PAC-Bayesian analysis on truncated differences of losses. Experimental results strongly back up our truncated min–max esti- mator. 1. Introduction. Our statistical task. Let Z1 = (X1,Y1),...,Zn = (Xn,Yn) be n 2 pairs of input–output and assume that each pair has been independently≥ drawn from the same unknown distribution P . Let denote the input space and let the output space be the set of real numbersX R, so that P is a proba- bility distribution on the product space , R.