DOCSLIB.ORG

Lecture 21: Conditional Distributions and Covariance / Correlation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 21: Conditional Distributions and Covariance / Correlation 6.3, 6.4 Conditional Distributions Conditional Probability / Distributions Let X and Y be random variables then Lecture 21: Conditional Distributions and Covariance / Conditional probability: Correlation P(X = x; Y = y) P(X = xjY = y) = P(Y = y) Statistics 104 f (x; y) f (xjy) = Colin Rundel fY (y) Product rule: April 9, 2012 P(X = x; Y = y) = P(X = xjY = y)P(Y = y) f (x; y) = f (xjy)fY (y) Statistics 104 (Colin Rundel) Lecture 21 April 9, 2012 1 / 23 6.3, 6.4 Conditional Distributions 6.3, 6.4 Conditional Distributions Bayes' Theorem and the Law of Total Probability Example - Conditional Uniforms Let X and Y be random variables then Let X ∼ Unif(0; 1) and Y jX ∼ Unif(x; 1), find f (x; y), fY (y), and f (xjy). Bayes' Theorem: f (x; y) f (yjx)f (x) f (xjy) = = X fY (y) fY (y) f (x; y) f (xjy)f (y) f (yjx) = = Y fX (x) fX (x) Law of Total Probability: Z 1 Z 1 fX (x) = f (x; y) dy = f (xjy)fY (y) dy −∞ −∞ Z 1 Z 1 fY (y) = f (x; y) dx = f (yjx)fX (x) dx −∞ −∞ Statistics 104 (Colin Rundel) Lecture 21 April 9, 2012 2 / 23 Statistics 104 (Colin Rundel) Lecture 21 April 9, 2012 3 / 23 6.3, 6.4 Conditional Distributions 6.3, 6.4 Conditional Expectation Independence and Conditional Distributions Conditional Expectation If X and Y are independent random variables then If X and Y are independent random variables then we define the conditional expectation as follows f (xjy) = f (x) 4.7 Conditional Expectation X 257 X The value of E(Y x) will not be uniquely defined for those values of x such that E(X jY = y) = xf (xjy) dx f (they marginaljx) = p.f.fY or( p.d.f.y| ) of X satisfies f (x) 0. However, since these values of x 1 = all y 256 Chapter 4 Expectation form a set of points whose probability is 0, the definition of E(Y x) at such a point | is irrelevant. (See Exercise 11 in Sec. 3.6.) It is also possible that there will be some Z 1 4.7 Conditional Expectation values of x such that the mean of the conditional distribution of Y given X x is Justification for this is straightundefined forward: for those x values. When the mean of Y exists and is finite, the set= of x E(X jY = y) = xf (xjy) dx Since expectations (including variances and covariances) are propertiesvalues forof distri- which the conditional mean is undefined has probability 0. −∞ butions, there will exist conditional versions of all such distributionalThe summaries expressions in Eqs. (4.7.1) and (4.7.2) are functions of x. These functions of as well as conditional versions of all theorems that we havef proven(x;cany or) be will computed laterfX (x)f beforeY (y)X is observed, and this idea leads to the following useful prove about expectations. In particular, suppose that we wish to predict one ran- f (xjy) = concept.= = fX (x) dom variable Y using a function d(X) of another random variablefY (y)X so as to fY (y) minimize E([Y d(X)]2). Then d(X) should be the conditional mean of Y given X. There is also− a very useful theorem that is anDefinition extension to expectationsConditional of Meansthe as Random Variables. Let h(x) stand for the function of x that is law of total probability. 4.7.2 denoted E(Y x) in either (4.7.1) or (4.7.2). Define the symbol E(Y X) to mean h(X) and call it the| conditional mean of Y given X. | Definition and Basic Properties In other words, E(Y X) is a random variable (a function of X) whose value when X x is E(Y x). Obviously,| we could define E(X Y)and E(X y) analogously. Example Household Survey. A collection of households were surveyed, and each= household| re- | | 4.7.1 ported the number of members and the number of automobiles owned. The reported numbers are in Table 4.1. Example Household Survey. Consider the household survey in Example 4.7.1. Let X be the Suppose that we were to sample a household at4.7.2 random fromnumber those households of members in a randomly selected household from the survey, and let Y be in the survey and learn the number of members. What would thenthe numberbe the expected of cars owned by that household. The 250 surveyed households are all number of automobiles that they own? equally likely to! be selected, so Pr(X x, Y y) is the number of households with = = The question at the end of Example 4.7.1 is closely relatedx members to the conditional and y cars, divided by 250. Those probabilities are reported in Table 4.2. Suppose that the sampled household has X 4 members. The conditional p.f. of Y distributionStatistics of one 104 random (Colin variable Rundel) given the other, as defined in Sec.Lecture 3.6. 21 April 9, 2012 4 / 23 Statistics 104 (Colin Rundel) Lecture 21 April 9, 2012 5 / 23 given X 4 is g (y 4) f(4, y)/f (4), which= is the x 4 column of Table 4.2 divided = 2 | = 1 = Definition Conditional Expectation/Mean. Let X and Y be random variablesby suchf1( that4) the0.208, mean namely, 4.7.1 of Y exists and is finite. The conditional expectation (or conditional mean)= of Y given g (0 4) 0.0385,g(1 4) 0.5769,g(2 4) 0.2885,g(3 4) 0.0962. X x is denoted by E(Y x) and is defined to be the expectation of the2 | conditional= 2 | = 2 | = 2 | = distribution= of Y given X| x. = The conditional mean of Y given X 4 is then = For example, if Y has a continuous conditional distribution6.3, given 6.4X xConditionalwith Expectation 6.3, 6.4 Conditional Expectation E(Y= 4) 0 0.0385 1 0.5769 2 0.2885 3 0.0962 1.442. conditional p.d.f. g2(y x), then | = × + × + × + × = | Similarly, we can compute E(Y x) for all eight values of x. They are E(Y x) ∞ yg (y x) dy. (4.7.1) | Example - Family| = 2 Cars| (Example 4.7.2 deGroot) Conditional Expectation as a Random Variable !−∞ x 12345678 Similarly, if Y has a discrete conditional distribution given X x with conditional p.f. g (y x), then = 2 | E(Y x) 0.609 1.057 1.317 1.442 1.538 1.533 1.75 2 Let X be the numberE(Y x) of membersyg (y x). in a randomly| (4.7.2) selected household and Y be the number of | = 2 | Based on the previous example we can see that the value of E(Y jX ) cars owned by that household.All y " changes depending on the value of x. Table 4.2 Joint p.f. f (x, y) of X and Y in Example 4.7.2 together with marginal Table 4.1 Reported numbers of household members and p.f.’s f1(x) and f2(y) automobiles in Example 4.7.1 As such we can think of the conditional expectation as being a function of x Number of members Number of the random variable X , thereby making E(Y jX ) itself a random variable, y 12345678f2(y) automobiles 12345678 0 0.040 0.028 0.012 0.008 0.008 0.004 0 0 0.100 which can be manipulated like any other random variable. 0 10 7 3 2 2 1 0 0 1 0.048 0.084 0.100 0.120 0.100 0.060 0.020 0.004 0.536 1 12 21 25 30 25 15 5 1 Law of Total Probability for Expectations: 2 1 5 10 15 20 11 5 3 2 0.004 0.020 0.040 0.060 0.080 0.044 0.020 0.012 0.280 302355321 3 0 0.008 0.012 0.020 0.020 0.012 0.008 0.004 0.084 f1(x) 0.092 0.140 0.164 0.208 0.208 0.120 0.048 0.020 Z 1 Z 1 Z 1 E[E(Y jX )] = E(Y jX = x)fX (x) dx = yf (yjx)fX (x) dy dx We can then calculate the expected number of cars in a household with 4 members as follows −∞ −∞ −∞ Z 1 Z 1 Z 1 Z 1 4 4 f (x; y) X X = y fX (x) dy dx = yf (x; y) dy dx E(Y jX = 4) = y · P(Y = yjX = 4) = y · P(X = 4; Y = y)=P(X = 4) −∞ −∞ fX (x) −∞ −∞ y=0 y=0 Z 1 Z 1 = y f (x; y) dx dy = 0 × 0:0385 + 1 × 0:5769 + 2 × 0:2885 + 3 × 0:0962 = 1:442 −∞ −∞ Similarly, we can calulcate E(Y jX ) for the other seven values of x Z 1 = yfY (y) dy = E(Y ) x 1 2 3 4 5 6 7 8 −∞ E(Y jX = x) 0.609 1.057 1.317 1.442 1.538 1.533 1.75 2 Statistics 104 (Colin Rundel) Lecture 21 April 9, 2012 6 / 23 Statistics 104 (Colin Rundel) Lecture 21 April 9, 2012 7 / 23 6.3, 6.4 Conditional Expectation 6.3, 6.4 Conditional Expectation Example - Family Cars, cont. (Example 4.7.2 deGroot) Example - Conditional Uniforms, cont. We can confirm the Law of Total Probability for Expectations using the Let X ∼ Unif(0; 1) and Y jX ∼ Unif(x; 1), find E(Y ).
Load more

Recommended publications
  • Lecture 22: Bivariate Normal Distribution Distribution
    6.5 Conditional Distributions General Bivariate Normal Let Z1; Z2 ∼ N (0; 1), which we will use to build a general bivariate normal Lecture 22: Bivariate Normal Distribution distribution. 1 1 2 2 f (z1; z2) = exp − (z1 + z2 ) Statistics 104 2π 2 We want to transform these unit normal distributions to have the follow Colin Rundel arbitrary parameters: µX ; µY ; σX ; σY ; ρ April 11, 2012 X = σX Z1 + µX p 2 Y = σY [ρZ1 + 1 − ρ Z2] + µY Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 1 / 22 6.5 Conditional Distributions 6.5 Conditional Distributions General Bivariate Normal - Marginals General Bivariate Normal - Cov/Corr First, lets examine the marginal distributions of X and Y , Second, we can find Cov(X ; Y ) and ρ(X ; Y ) Cov(X ; Y ) = E [(X − E(X ))(Y − E(Y ))] X = σX Z1 + µX h p i = E (σ Z + µ − µ )(σ [ρZ + 1 − ρ2Z ] + µ − µ ) = σX N (0; 1) + µX X 1 X X Y 1 2 Y Y 2 h p 2 i = N (µX ; σX ) = E (σX Z1)(σY [ρZ1 + 1 − ρ Z2]) h 2 p 2 i = σX σY E ρZ1 + 1 − ρ Z1Z2 p 2 2 Y = σY [ρZ1 + 1 − ρ Z2] + µY = σX σY ρE[Z1 ] p 2 = σX σY ρ = σY [ρN (0; 1) + 1 − ρ N (0; 1)] + µY = σ [N (0; ρ2) + N (0; 1 − ρ2)] + µ Y Y Cov(X ; Y ) ρ(X ; Y ) = = ρ = σY N (0; 1) + µY σX σY 2 = N (µY ; σY ) Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 2 / 22 Statistics 104 (Colin Rundel) Lecture 22 April 11, 2012 3 / 22 6.5 Conditional Distributions 6.5 Conditional Distributions General Bivariate Normal - RNG Multivariate Change of Variables Consequently, if we want to generate a Bivariate Normal random variable Let X1;:::; Xn have a continuous joint distribution with pdf f defined of S.
    [Show full text]
  • Chapter 6 Continuous Random Variables and Probability
    EF 507 QUANTITATIVE METHODS FOR ECONOMICS AND FINANCE FALL 2019 Chapter 6 Continuous Random Variables and Probability Distributions Chap 6-1 Probability Distributions Probability Distributions Ch. 5 Discrete Continuous Ch. 6 Probability Probability Distributions Distributions Binomial Uniform Hypergeometric Normal Poisson Exponential Chap 6-2/62 Continuous Probability Distributions § A continuous random variable is a variable that can assume any value in an interval § thickness of an item § time required to complete a task § temperature of a solution § height in inches § These can potentially take on any value, depending only on the ability to measure accurately. Chap 6-3/62 Cumulative Distribution Function § The cumulative distribution function, F(x), for a continuous random variable X expresses the probability that X does not exceed the value of x F(x) = P(X £ x) § Let a and b be two possible values of X, with a < b. The probability that X lies between a and b is P(a < X < b) = F(b) -F(a) Chap 6-4/62 Probability Density Function The probability density function, f(x), of random variable X has the following properties: 1. f(x) > 0 for all values of x 2. The area under the probability density function f(x) over all values of the random variable X is equal to 1.0 3. The probability that X lies between two values is the area under the density function graph between the two values 4. The cumulative density function F(x0) is the area under the probability density function f(x) from the minimum x value up to x0 x0 f(x ) = f(x)dx 0 ò xm where
    [Show full text]
  • Extremal Dependence Concepts
    Extremal dependence concepts Giovanni Puccetti1 and Ruodu Wang2 1Department of Economics, Management and Quantitative Methods, University of Milano, 20122 Milano, Italy 2Department of Statistics and Actuarial Science, University of Waterloo, Waterloo, ON N2L3G1, Canada Journal version published in Statistical Science, 2015, Vol. 30, No. 4, 485{517 Minor corrections made in May and June 2020 Abstract The probabilistic characterization of the relationship between two or more random variables calls for a notion of dependence. Dependence modeling leads to mathematical and statistical challenges and recent developments in extremal dependence concepts have drawn a lot of attention to probability and its applications in several disciplines. The aim of this paper is to review various concepts of extremal positive and negative dependence, including several recently established results, reconstruct their history, link them to probabilistic optimization problems, and provide a list of open questions in this area. While the concept of extremal positive dependence is agreed upon for random vectors of arbitrary dimensions, various notions of extremal negative dependence arise when more than two random variables are involved. We review existing popular concepts of extremal negative dependence given in literature and introduce a novel notion, which in a general sense includes the existing ones as particular cases. Even if much of the literature on dependence is focused on positive dependence, we show that negative dependence plays an equally important role in the solution of many optimization problems. While the most popular tool used nowadays to model dependence is that of a copula function, in this paper we use the equivalent concept of a set of rearrangements.
    [Show full text]
  • Joint Probability Distributions
    ST 380 Probability and Statistics for the Physical Sciences Joint Probability Distributions In many experiments, two or more random variables have values that are determined by the outcome of the experiment. For example, the binomial experiment is a sequence of trials, each of which results in success or failure. If ( 1 if the i th trial is a success Xi = 0 otherwise; then X1; X2;:::; Xn are all random variables defined on the whole experiment. 1 / 15 Joint Probability Distributions Introduction ST 380 Probability and Statistics for the Physical Sciences To calculate probabilities involving two random variables X and Y such as P(X > 0 and Y ≤ 0); we need the joint distribution of X and Y . The way we represent the joint distribution depends on whether the random variables are discrete or continuous. 2 / 15 Joint Probability Distributions Introduction ST 380 Probability and Statistics for the Physical Sciences Two Discrete Random Variables If X and Y are discrete, with ranges RX and RY , respectively, the joint probability mass function is p(x; y) = P(X = x and Y = y); x 2 RX ; y 2 RY : Then a probability like P(X > 0 and Y ≤ 0) is just X X p(x; y): x2RX :x>0 y2RY :y≤0 3 / 15 Joint Probability Distributions Two Discrete Random Variables ST 380 Probability and Statistics for the Physical Sciences Marginal Distribution To find the probability of an event defined only by X , we need the marginal pmf of X : X pX (x) = P(X = x) = p(x; y); x 2 RX : y2RY Similarly the marginal pmf of Y is X pY (y) = P(Y = y) = p(x; y); y 2 RY : x2RX 4 / 15 Joint
    [Show full text]
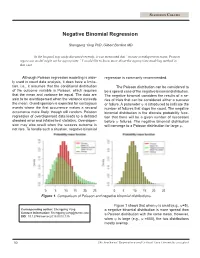
  • Negative Binomial Regression
    STATISTICS COLUMN Negative Binomial Regression Shengping Yang PhD ,Gilbert Berdine MD In the hospital stay study discussed recently, it was mentioned that “in case overdispersion exists, Poisson regression model might not be appropriate.” I would like to know more about the appropriate modeling method in that case. Although Poisson regression modeling is wide- regression is commonly recommended. ly used in count data analysis, it does have a limita- tion, i.e., it assumes that the conditional distribution The Poisson distribution can be considered to of the outcome variable is Poisson, which requires be a special case of the negative binomial distribution. that the mean and variance be equal. The data are The negative binomial considers the results of a se- said to be overdispersed when the variance exceeds ries of trials that can be considered either a success the mean. Overdispersion is expected for contagious or failure. A parameter ψ is introduced to indicate the events where the first occurrence makes a second number of failures that stops the count. The negative occurrence more likely, though still random. Poisson binomial distribution is the discrete probability func- regression of overdispersed data leads to a deflated tion that there will be a given number of successes standard error and inflated test statistics. Overdisper- before ψ failures. The negative binomial distribution sion may also result when the success outcome is will converge to a Poisson distribution for large ψ. not rare. To handle such a situation, negative binomial 0 5 10 15 20 25 0 5 10 15 20 25 Figure 1. Comparison of Poisson and negative binomial distributions.
    [Show full text]
  • Section 1: Regression Review
    Section 1: Regression review Yotam Shem-Tov Fall 2015 Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 1 / 58 Contact information Yotam Shem-Tov, PhD student in economics. E-mail: [email protected]. Office: Evans hall room 650 Office hours: To be announced - any preferences or constraints? Feel free to e-mail me. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 2 / 58 R resources - Prior knowledge in R is assumed In the link here is an excellent introduction to statistics in R . There is a free online course in coursera on programming in R. Here is a link to the course. An excellent book for implementing econometric models and method in R is Applied Econometrics with R. This is my favourite for starting to learn R for someone who has some background in statistic methods in the social science. The book Regression Models for Data Science in R has a nice online version. It covers the implementation of regression models using R . A great link to R resources and other cool programming and econometric tools is here. Yotam Shem-Tov STAT 239A/ PS 236A September 3, 2015 3 / 58 Outline There are two general approaches to regression 1 Regression as a model: a data generating process (DGP) 2 Regression as an algorithm (i.e., an estimator without assuming an underlying structural model). Overview of this slides: 1 The conditional expectation function - a motivation for using OLS. 2 OLS as the minimum mean squared error linear approximation (projections). 3 Regression as a structural model (i.e., assuming the conditional expectation is linear).
    [Show full text]
  • (Introduction to Probability at an Advanced Level) - All Lecture Notes
    Fall 2018 Statistics 201A (Introduction to Probability at an advanced level) - All Lecture Notes Aditya Guntuboyina August 15, 2020 Contents 0.1 Sample spaces, Events, Probability.................................5 0.2 Conditional Probability and Independence.............................6 0.3 Random Variables..........................................7 1 Random Variables, Expectation and Variance8 1.1 Expectations of Random Variables.................................9 1.2 Variance................................................ 10 2 Independence of Random Variables 11 3 Common Distributions 11 3.1 Ber(p) Distribution......................................... 11 3.2 Bin(n; p) Distribution........................................ 11 3.3 Poisson Distribution......................................... 12 4 Covariance, Correlation and Regression 14 5 Correlation and Regression 16 6 Back to Common Distributions 16 6.1 Geometric Distribution........................................ 16 6.2 Negative Binomial Distribution................................... 17 7 Continuous Distributions 17 7.1 Normal or Gaussian Distribution.................................. 17 1 7.2 Uniform Distribution......................................... 18 7.3 The Exponential Density...................................... 18 7.4 The Gamma Density......................................... 18 8 Variable Transformations 19 9 Distribution Functions and the Quantile Transform 20 10 Joint Densities 22 11 Joint Densities under Transformations 23 11.1 Detour to Convolutions......................................
    [Show full text]
  • Probability for Statistics: the Bare Minimum Prerequisites
    Probability for Statistics: The Bare Minimum Prerequisites This note seeks to cover the very bare minimum of topics that students should be familiar with before starting the Probability for Statistics module. Most of you will have studied classical and/or axiomatic probability before, but given the various backgrounds it's worth being concrete on what students should know going in. Real Analysis Students should be familiar with the main ideas from real analysis, and at the very least be familiar with notions of • Limits of sequences of real numbers; • Limit Inferior (lim inf) and Limit Superior (lim sup) and their connection to limits; • Convergence of sequences of real-valued vectors; • Functions; injectivity and surjectivity; continuous and discontinuous functions; continuity from the left and right; Convex functions. • The notion of open and closed subsets of real numbers. For those wanting for a good self-study textbook for any of these topics I would recommend: Mathematical Analysis, by Malik and Arora. Complex Analysis We will need some tools from complex analysis when we study characteristic functions and subsequently the central limit theorem. Students should be familiar with the following concepts: • Imaginary numbers, complex numbers, complex conjugates and properties. • De Moivre's theorem. • Limits and convergence of sequences of complex numbers. • Fourier transforms and inverse Fourier transforms For those wanting a good self-study textbook for these topics I recommend: Introduction to Complex Analysis by H. Priestley. Classical Probability and Combinatorics Many students will have already attended a course in classical probability theory beforehand, and will be very familiar with these basic concepts.
    [Show full text]
  • Using Learned Conditional Distributions As Edit Distance Jose Oncina, Marc Sebban
    Using Learned Conditional Distributions as Edit Distance Jose Oncina, Marc Sebban To cite this version: Jose Oncina, Marc Sebban. Using Learned Conditional Distributions as Edit Distance. Structural, Syntactic, and Statistical Pattern Recognition, Joint IAPR International Workshops, SSPR 2006 and SPR 2006, Aug 2006, Hong Kong, China. pp 403-411, ISBN 3-540-37236-9. hal-00322429 HAL Id: hal-00322429 https://hal.archives-ouvertes.fr/hal-00322429 Submitted on 18 Sep 2008 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Using Learned Conditional Distributions as Edit Distance⋆ Jose Oncina1 and Marc Sebban2 1 Dep. de Lenguajes y Sistemas Informaticos,´ Universidad de Alicante (Spain) [email protected] 2 EURISE, Universite´ de Saint-Etienne, (France) [email protected] Abstract. In order to achieve pattern recognition tasks, we aim at learning an unbiased stochastic edit distance, in the form of a finite-state transducer, from a corpus of (input,output) pairs of strings. Contrary to the state of the art methods, we learn a transducer independently on the marginal probability distribution of the input strings. Such an unbiased way to proceed requires to optimize the pa- rameters of a conditional transducer instead of a joint one.
    [Show full text]
  • Multivariate Rank Statistics for Testing Randomness Concerning Some Marginal Distributions
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector JOURNAL OF MULTIVARIATE ANALYSIS 5, 487-496 (1975) Multivariate Rank Statistics for Testing Randomness Concerning Some Marginal Distributions MARIE HuS~ovli Department of Statistics, CharZes University, Prague, Czechoskwahia Communicated by P. K. Sen In the present paper there is proposed a rank statistic for multivariate testing of randomness concerning some marginal distributions. The asymptotic distribu- tion of this statistic under hypothesis and “near” alternatives is treated. 1. INTRODUCTION Let Xj = (X, ,..., XJ, j = I,..., IV, be independent p-dimensional random variables and letF,&, y) andFdj(x) denote the distribution function of (Xii , XV!) and X,, , respectively. Fi, is assumedcontinuous throughout the whole paper, i=l ,..., p,j = l,...) N. We are interested in testing hypothesis of randomness of the univariate marginal distributions: for all x, i = l,..., p, j = 1,. N (1.1) against for all x, i = I,..., p, j = I ,..., N, (1.2) where $,, are unknown parameters. Or more generally, we are interested in testing hypothesis of randomnessassociated with some marginal distributions: F,“(x”) = F”(X”), u = l,..., Y, j = l,..., N, (1.3) against F,y(X”) = qx”; El;), Y = l,..., r, j = I,..., N, (1.4) Received September 1974; revised April 15, 1975. AMS subject classifications: Primary 62G10, Secondary 62HlO. Key words and phrases: Rank statistics; Testing randomness, Asymptotic distribution. 487 Copyright 0 1975 by Academic Press, Inc. All rights of reproduction in any form reserved. 488 MARIE HU?,KOVsi where FjV(xy) is the marginal distribution of the subvector Xy, Y = I,..., r, Xl ,***>x7, is a partition of the vector x, i.e., x’ = (xl’,..., xr’) and Oj’ = (0,” ,..., 0;‘) is a vector of unknown parameters.
    [Show full text]
  • Random Variables and Probability Distributions
    Schaum's Outline of Probability and Statistics CHAPTERCHAPTER 122 Random Variables and Probability Distributions Random Variables Suppose that to each point of a sample space we assign a number. We then have a function defined on the sam- ple space. This function is called a random variable (or stochastic variable) or more precisely a random func- tion (stochastic function). It is usually denoted by a capital letter such as X or Y. In general, a random variable has some specified physical, geometrical, or other significance. EXAMPLE 2.1 Suppose that a coin is tossed twice so that the sample space is S ϭ {HH, HT, TH, TT}. Let X represent the number of heads that can come up. With each sample point we can associate a number for X as shown in Table 2-1. Thus, for example, in the case of HH (i.e., 2 heads), X ϭ 2 while for TH (1 head), X ϭ 1. It follows that X is a random variable. Table 2-1 Sample Point HH HT TH TT X 2110 It should be noted that many other random variables could also be defined on this sample space, for example, the square of the number of heads or the number of heads minus the number of tails. A random variable that takes on a finite or countably infinite number of values (see page 4) is called a dis- crete random variable while one which takes on a noncountably infinite number of values is called a nondiscrete random variable. Discrete Probability Distributions Let X be a discrete random variable, and suppose that the possible values that it can assume are given by x1, x2, x3, .
    [Show full text]
  • Large Scale Conditional Covariance Matrix Modeling, Estimation and Testing
    Large Scale Conditional Covariance Matrix Modeling, Estimation and Testing Zhuanxin Ding1 Frank Russell Company, Tacoma, WA 98401, USA and Robert F. Engle University of California, San Diego, La Jolla, CA 92093, USA June 1996 This Revision May 2001 Abstract A new representation of the diagonal Vech model is given using the Hadamard product. Sufficient conditions on parameter matrices are provided to ensure the positive definiteness of covariance matrices from the new representation. Based on this, some new and simple models are discussed. A set of diagnostic tests for multivariate ARCH models is proposed. The tests are able to detect various model misspecifications by examing the orthogonality of the squared normalized residuals. A small Monte-Carlo study is carried out to check the small sample performance of the test. An empirical example is also given as guidance for model estimation and selection in the multivariate framework. For the specific data set considered, it is found that the simple one and two parameter models and the constant conditional correlation model perform fairly well. Keywords: conditional covariance, Multivariate ARCH, Hadamard product, M-test. 1 We would like to thank Clive Granger, Hong-Ye Gao, Doug Martin, Jeffrey Wang and Hal White for many helpful discussions. 2 1. Introduction It has now become common knowledge that the risk of the financial market, which is mainly represented by the variance of individual stock returns and the covariance between different assets or with the market, is highly forecastable. The research in this area however is far from complete and the application of different econometric models is just at its beginning.
    [Show full text]