Table 25 Distribution Coeffcients K Determined from Feldspar-Fluid And
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Single-Crystal Epr Study of Radiation-Induced Defects
A SINGLE-CRYSTAL EPR STUDY OF RADIATION-INDUCED DEFECTS IN SELECTED SILICATES A Thesis Submitted to the College of Graduate Studies and Research In Partial Fulfillment of the Requirements For the Degree of Doctor of Philosophy In the Department of Geological Sciences University of Saskatchewan Saskatoon By Mao Mao Copyright Mao Mao, October, 2012. All rights reserved. Permission to Use In presenting this thesis in partial fulfilment of the requirements for a Doctor of Philosophy degree from the University of Saskatchewan, I agree that the Libraries of this University may make it freely available for inspection. I further agree that permission for copying of this thesis in any manner, in whole or in part, for scholarly purposes may be granted by the professor or professors who supervised my thesis work or, in their absence, by the Head of the Department or the Dean of the College in which my thesis work was done. It is understood that any copying or publication or use of this thesis or parts thereof for financial gain shall not be allowed without my written permission. It is also understood that due recognition shall be given to me and to the University of Saskatchewan in any scholarly use which may be made of any material in my thesis. Requests for permission to copy or to make other use of material in this thesis in whole or part should be addressed to: Head of the Department of Geological Sciences 114 Science Place University of Saskatchewan Saskatoon, Saskatchewan S7N5E2, Canada i Abstract This thesis presents a series of single-crystal electron paramagnetic resonance (EPR) studies on radiation-induced defects in selected silicate minerals, including apophyllites, prehnite, and hemimorphite, not only providing new insights to mechanisms of radiation-induced damage in minerals but also having direct relevance to remediation of heavy metalloid contamination and nuclear waste disposal. -

THB Avterican Mtxeralocist
THB AvtERICAN MtxERALocIST JOURNAL OF THE MINERALOGICAL SOCIETY OF AMERICA Vol. 49 JUL\'-AUGUST, 1964 Nos. 7 and 8 BUDDINGTONITE, AN AMMONIUM FELDSPAR WITH ZEOLITIC WATER1 Rrcn,lno C. Ent, DoNaro E. Wnrro, Josorn J. Faunv eNo Dower-o E. Lno, U. S. Geol,ogicolSurttey, Menlo Park, Calif ., and' Wash'ington,D' C. Arsrn,q.ct Buddingtonite, the first ammonium aluminosilicate found in nature, occurs in Quater- nary andesite and older rocks hydrothermally altered by ammonia-bearing hot-spring waters below the water table at the Sulphur Bank quicksilver mine, Lake county, cali- fornia. Typicaliy, it occurs as compact masses pseudomorphous after plagioclase, and as crystals as much as 0.05 mm diameter lining cavities. Buddingtonite is biaxial (*), a:1.530,0:1'531, r:1.534 all *0'002,2V not de- terrnined,X/1a:4',2:b,Y Ac:19'. H 5+, G2.32+0.01- Chemical analysis of purest separate gave: SiOz,63.80;A1:Or, 19.16; FezOe, 1'85; MgO' 0.21; CaO,0.04; BaO, 0.26; NarO, 0.06; KzO, 0.62; (NHr)rO, 7.95;TiO2,0.99; HzO-, 0'88; HzO+,3.28; S, 1.59;total 100.69(-O+S):100.10 per cent. Buddingtonite is monoclinic; P21or P21fm;a:8.571,b:13.032,c:7.187,A:ll2o44' !l'; a:b:c:0.658:1:0.551; cell volume, 7+0.42fu;ceil contents4[NHdISirOs'1/2HzO]; calculated density, 2.38s gcm-3. From 370" to 430. c, buddingtonite is the ammonium analogue of monoclinic K-feld- spar; below about 370' C with normal atmospheric moisture, buddingtonite adsorbs zeo- Iitic water. -

Nho* in Pegmatitic Feldspars from the Southern Black Hills, South Dakota
American Mineralogist, Volume 73, pages 818-82I , 1988 NHo* in pegmatitic feldspars from the southern Black Hills, South Dakota G. Cr,nvn SolovroNrr Gnoncn R. RossNr.q.N Division of Geological and Planetary Sciences,2California Institute of Technology, Pasadena,California 91125, U.S.A. Ansrru,cr Trace amounts of ammonium ion (0.7 molo/oNHo* substitution) have been identified from the infrared spectra of alkali feldspars from pegmatites occurring in the southern Black Hills district, South Dakota. The spectroscopicdata indicate that the ammonium is structurally bound, most likely in the M site of the microcline. These results indicate that ammonium was likely a component of metamorphic fluids present during anatexis of metasedimentaryrocks in the southern Black Hills district. INrnonucrroN cent materialintimately mixed with sinuouspatches of turbid materialin a typicalperthitic intergrowth. In the clearregions, Buddingtonite, the feldspar in which NHf, substitutes no inclusions-fluid or solid-were observedmicroscopically. for K+ in the M site, was first discovered in a low-tem- The slabs,mounted over brassapertures that rangedfrom 2.0 perature, ammonium-rich environment (Erd et al., 19 6 4). to 0.5 mm, werepositioned so that the beamavoided strongly Both buddingtonite and K-feldspars with variable am- turbid zones.The slabsranged in thicknessfrom 0.20 to 0.80 monium contents have subsequentlybeen found in a va- mm for measurementsin the 4000- to 2500-cm-' regionand riety of localities where rocks have been hydrothermally weregreater than -

Italian Type Minerals / Marco E
THE AUTHORS This book describes one by one all the 264 mi- neral species first discovered in Italy, from 1546 Marco E. Ciriotti was born in Calosso (Asti) in 1945. up to the end of 2008. Moreover, 28 minerals He is an amateur mineralogist-crystallographer, a discovered elsewhere and named after Italian “grouper”, and a systematic collector. He gradua- individuals and institutions are included in a pa- ted in Natural Sciences but pursued his career in the rallel section. Both chapters are alphabetically industrial business until 2000 when, being General TALIAN YPE INERALS I T M arranged. The two catalogues are preceded by Manager, he retired. Then time had come to finally devote himself to his a short presentation which includes some bits of main interest and passion: mineral collecting and information about how the volume is organized related studies. He was the promoter and is now the and subdivided, besides providing some other President of the AMI (Italian Micromineralogical As- more general news. For each mineral all basic sociation), Associate Editor of Micro (the AMI maga- data (chemical formula, space group symmetry, zine), and fellow of many organizations and mine- type locality, general appearance of the species, ralogical associations. He is the author of papers on main geologic occurrences, curiosities, referen- topological, structural and general mineralogy, and of a mineral classification. He was awarded the “Mi- ces, etc.) are included in a full page, together cromounters’ Hall of Fame” 2008 prize. Etymology, with one or more high quality colour photogra- geoanthropology, music, and modern ballet are his phs from both private and museum collections, other keen interests. -

Shin-Skinner January 2018 Edition
Page 1 The Shin-Skinner News Vol 57, No 1; January 2018 Che-Hanna Rock & Mineral Club, Inc. P.O. Box 142, Sayre PA 18840-0142 PURPOSE: The club was organized in 1962 in Sayre, PA OFFICERS to assemble for the purpose of studying and collecting rock, President: Bob McGuire [email protected] mineral, fossil, and shell specimens, and to develop skills in Vice-Pres: Ted Rieth [email protected] the lapidary arts. We are members of the Eastern Acting Secretary: JoAnn McGuire [email protected] Federation of Mineralogical & Lapidary Societies (EFMLS) Treasurer & member chair: Trish Benish and the American Federation of Mineralogical Societies [email protected] (AFMS). Immed. Past Pres. Inga Wells [email protected] DUES are payable to the treasurer BY January 1st of each year. After that date membership will be terminated. Make BOARD meetings are held at 6PM on odd-numbered checks payable to Che-Hanna Rock & Mineral Club, Inc. as months unless special meetings are called by the follows: $12.00 for Family; $8.00 for Subscribing Patron; president. $8.00 for Individual and Junior members (under age 17) not BOARD MEMBERS: covered by a family membership. Bruce Benish, Jeff Benish, Mary Walter MEETINGS are held at the Sayre High School (on Lockhart APPOINTED Street) at 7:00 PM in the cafeteria, the 2nd Wednesday Programs: Ted Rieth [email protected] each month, except JUNE, JULY, AUGUST, and Publicity: Hazel Remaley 570-888-7544 DECEMBER. Those meetings and events (and any [email protected] changes) will be announced in this newsletter, with location Editor: David Dick and schedule, as well as on our website [email protected] chehannarocks.com. -
![Usgeorosicar',)Ljii;'?'Ix",Ihi'f; I.'""':';:I%:1L|;'Ffi].]:St""'Mser''](https://docslib.b-cdn.net/cover/6802/usgeorosicar-ljii-ix-ihif-i-i-1l-ffi-st-mser-3426802.webp)
Usgeorosicar',)Ljii;'?'Ix",Ihi'f; I.'""':';:I%:1L|;'Ffi].]:St""'Mser''
American Mineralogist, Volume 78, pages204-209, 1993 Holotype buddingtonite:An ammoniumfeldspar without zeolitic HrO J.H.L. VoNCKEN,* H.L.M. vAN RSERMUNDT** A.M.J. vAN DER EnnonN, J.B.H. Jl.NsnN Facultyof EarthSciences, Department of ChemicalGeology, Budapestlaan 4, 3508TA Utrecht,The Netherlands R. C. Eno uSGeorosicar',)lJii;'?'ix",iHi'f; i.'""':';:i%:1l|;'ffi].]:sT""'Mser'' Ansrucr Holotype buddingtonite from the Sulphur Bank Quicksilver deposit, Lake County, Cal- ifornia, was studied by XRD, IR, STEM, SEM, TGA, DTA and wet chemical analyses. Synthetic anhydrous ammonium feldspar was studied also for comparison. The holotype buddingtonite specimen(NMNH no. I1697400) contains admixtures of FeSr,anatase and, most importantly, montmorillonite. Montmorillonite is capableof reversibledehydration, and its admixture explains the zeolitic behavior previously ascribed to buddingtonite. It is concluded that buddingtonite is an anhydrous ammonium feldspar: i.e., free of zeolitic HrO, with no zeolitic properties. INtnooucrroN the HrO is not present in an ordered way (Kimball and Megaw, 1974). Moreover, structure and properties of Buddingtonite was first describedby Erd et al. (1964) synthetic ammonium feldspar are consistentwith the an- as an ammonium feldspar with zeolitic HrO, with the hydrous formula NHoAlSi3Os(Voncken et al., 1988; following formula: NHoAlSi3Os't/zH2O.The mineral was Voncken, 1990). In addition, the lattice parametersand studied by chemical analysis,XRD, thermal analysis,and X-ray diffraction pattern of synthetic ammonium feld- IR. Buddingtonite was found initially as a hydrothermal spar are essentiallyidentical to those of natural ammo- replacementof plagioclasoin certain parts of the Sulphur nium feldspar, suggestingthat differencesin properties Bank Quicksilver deposit,Lake County, California (White between natural and synthetic ammonium feldspar are and Robertson,1962), and later in oil shalesand hydro- due to impurities in the natural material. -

Holotype Buddingtonite: an Ammonium Feldspar Without Zeolitic H20
American Mineralogist, Volume 78, pages 204-209, 1993 Holotype buddingtonite: An ammonium feldspar without zeolitic H20 J.H.L. VONCKEN,* H.L.M. VAN ROERMUND,** A.M.J. VAN DER EERDEN, J.D.H. JANSEN Faculty of Earth Sciences, Department of Chemical Geology, Budapestlaan 4, 3508 TA Utrecht, The Netherlands R.C.ERD U.S. Geological Survey, Branch of Igneous and Geothermal Processes, MS910, 345 Middlefield Road, Menlo Park, California, U.S.A. ABSTRACT Holotype buddingtonite from the Sulphur Bank Quicksilver deposit, Lake County, Cal- ifornia, was studied by XRD, IR, STEM, SEM, TGA, DT A and wet chemical analyses. Synthetic anhydrous ammonium feldspar was studied also for comparison. The holotype buddingtonite specimen (NMNH no. 11697400) contains admixtures ofFeS2, anatase and, most importantly, montmorillonite. Montmorillonite is capable of reversible dehydration, and its admixture explains the zeolitic behavior previously ascribed to buddingtonite. It is concluded that buddingtonite is an anhydrous ammonium feldspar: i.e., free of zeolitic H20, with no zeolitic properties. INTRODUCTION the H20 is not present in an ordered way (Kimball and Buddingtonite was first described by Erd et al. (1964) Megaw, 1974). Moreover, structure and properties of as an ammonium feldspar with zeolitic H20, with the synthetic ammonium feldspar are consistent with the an- following formula: NH4AISi30g. IhH20. The mineral was hydrous formula NH4AISi30g (Voncken et aI., 1988; studied by chemical analysis, XRD, thermal analysis, and Voncken, 1990). In addition, the -

U. S. Department of the Interior U.S. Geological
uses science for a changing world U. S. DEPARTMENT OF THE INTERIOR U.S. GEOLOGICAL SURVEY BULK MINERALOGY, MICROMEVERALOGY, AND AUTHIGENIC MINERALS IN THE MEADE PEAK PHOSPHATIC SHALE MEMBER OF THE PHOSPHORIA FORMATION, SOUTHEASTERN IDAHO By George A. Desborough i , Russell G. Tysdal 1 , Andrew C. Knudsen 01, Richard I. Grauch , James R. Herring1, and Isabelle Brownfield1 OPEN-FILE REPORT 01-0004 Prepared In Collaboration with: U.S. Bureau of Land Management U.S. Forest Service Agrium U.S. Inc. Astaris LLC J.R. Simplot Company Monsanto Company Rhodia Inc. This report is preliminary and has not been reviewed for conformity with United States Geological Survey editorial Standards or with the North American Stratigraphic Code. Any use of trade, product or firm names is for descriptive Purposes only and does not imply endorsement by the U.S. Government 'U.S. Geological Survey, Denver, CO 80225; 2University of Idaho, Department of Geological Sciences, Moscow, ID 83844 CONTENTS Page Abstract.......................................................................................3 Introduction................................................................................. 3 Background........................................................................ 3 Geologic Setting...................................................................4 Mineralogy of less-weathered strata.....................................................4 Authigenic feldspars in the middle waste......................................6 Scanning electron microscope studies -

Buddingtonite (NH4-Feldspar) in the Condor Oilshale Deposit, Queensland, Australia
MINERALOGICAL MAGAZINE, SEPTEMBER 1983, VOL. 47, PP. 327-34 Buddingtonite (NH4-feldspar) in the Condor Oilshale Deposit, Queensland, Australia F. C. LOUGI'tNAN AND F. IVOR ROBERTS School of Applied Geology, Unversity of NSW, Kensington, Australia AND A. W. LINDNER Southern Pacific Petroleum, Sydney, Australia ABSTRACT. Buddingtonite of similar composition and tonite at Sulphur Bank occurs within altered properties to that described from the type area, is andesites and was considered by Erd et al. (1964) to uniformly distributed throughout the upper 600 m of have resulted from reaction of ammonium-rich,hot strata in the Condor Oilshale Deposit near Proserpine, spring waters with plagioclase. Gulbrandsen (1974) Queensland. The mineral, which constitutes up to 16~ on the other hand, attributed the presence of the and averages nearly 10 ~o of the strata, is associated with abundant montmorillonite, siderite, and quartz as well as mineral in the Phosphoria Formation to dia- minor amounts of disordered kaolinite, iUite, calcite, genesis. pyrite, cristobalite, and an unnamedspecies of tliejahnsite Recently, buddingtonite of similar composition group. The buddingtonite is concluded to be of diagenetic to that at Sulphur Bank was encountered in several origin. It developed in an ammonium-rich environment, samples from the Early Tertiary Condor Oilshale most probably at significant depth within the mud Deposit near Proserpine in central coastal Queens- beneath a stratified lake. Its progenitor, however, remains land (fig. 1) and an ensuing systematic study of the unknown. The occurrence of this mineral is also of interest in that ammonia could prove an important by-product in the commercial exploitation of the oilshales. -
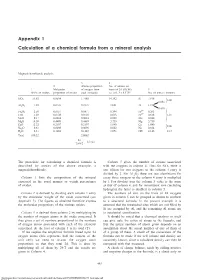
Appendix 1 Calculation of a Chemical Formula from a Mineral Analysis
Appendix 1 Calculation of a chemical formula from a mineral analysis Appendix 1 Magnesiohornblende analysis 3 4 2 Atomic proportion No. of anions on 1 Molecular of oxygen from basis of 24 (O,OH) 5 Wt.% of oxides proportion of oxides each molecule i.e. col. 368.3735 No. of ions in formula SiO 51.63 0.8594 1.7188 14.392 Si 7.196 2 8.00 0.804 } Al2O3 7.39 0.0725 0.2175 1.821 Al 1.214 0.410 3+ Fe2O3 2.50 0.0157 0.0471 0.394 Fe 0.263 FeO 5.30 0.0738 0.0738 0.618 Fe2+ 0.618 5.07 MnO 0.17 0.0024 0.0024 0.020 Mn 0.020 } MgO 18.09 0.4489 0.4489 3.759 Mg 3.759 CaO 12.32 0.2197 0.2197 1.840 Ca 1.840 2.00 Na2O 0.61 0.0098 0.0098 0.082 Na 0.164 } H2O+ 2.31 0.1282 0.1282 1.073 OH 2.146 2.15 Total 100.32 2.8662 24 = 8.3735 2.8662 The procedure for calculating a chemical formula is Column 5 gives the number of cations associated described by means of the above example, a with the oxygens in column 4. Thus for SiO2 there is magnesiohornblende. one silicon for two oxygens so the column 4 entry is divided by 2. For A12O3 there are two aluminiums for Column 1 lists the composition of the mineral every three oxygens so the column 4 entry is multiplied expressed in the usual manner as weight percentages by ~˜. -

Nitrogen Geochemistry As a Tracer of Fluid Flow in a Hydrothermal Vent
Available online at www.sciencedirect.com Geochimica et Cosmochimica Acta 72 (2008) 4929–4947 www.elsevier.com/locate/gca Nitrogen geochemistry as a tracer of fluid flow in a hydrothermal vent complex in the Karoo Basin, South Africa Henrik Svensen a,*, Gray Bebout b, Andreas Kronz c, Long Li b, Sverre Planke a,d, Luc Chevallier e,Bjørn Jamtveit a a Physics of Geological Processes (PGP), Department of Physics, University of Oslo, P.O. Box 1048, Blindern, Norway b Department of Earth and Environmental Sciences, Lehigh University, Bethlehem, PA 18015-3188, USA c Geowissenschaftliches Zentrum, University of Goettingen, Goldschmidt-Strasse 1, D-37077 Goettingen, Germany d Volcanic Basin Petroleum Research (VBPR), Oslo Research Park, Oslo, Norway e Council for Geoscience, P.O. Box 572, Bellville 7535, Cape Town, South Africa Received 28 January 2008; accepted in revised form 31 July 2008; available online 7 August 2008 Abstract We have investigated the N geochemistry of minerals and rocks from contact metamorphic aureoles and hydrothermal vent complexes (HVC) in the Karoo Basin in South Africa. The HVC formed during phreatic eruptions associated with rapid devolatilization and pressure build-up in contact aureoles around early Jurassic sill intrusions. By combining outcrop data from a HVC and core data from contact aureoles, we investigate the relationship between light element release during metamorphism and vertical fluid migration. Sandstone and breccia from the HVC contain early-diagenetic ammonium þ NH4 -bearing feldspar (buddingtonite) and illite. Ammonium occupies up to 95% of the A site in feldspar, corresponding to concentrations up to 5.2 wt% N. Bulk-rock N isotope data for rocks from inside and outside the hydrothermal vent com- 15 plex fall into two distinct groups. -

Mineral Mapping at Cuprite, Nevada with a 63-Channel Imaging Spectrometer
Mineral Mapping at Cuprite, Nevada with a 63-Channel Imaging Spectrometer F. A. Kruse, K. S. Kierein-Young, and 1. W. Boardman Center for the Study of Earth from Space (CSES), Cooperative Institute for Research in Environmental Sciences (CIRES), University of Colorado, Boulder, CO 80309-0449 ABSTRACT:Geophysical and Environmental Research Imaging Spectrometer (GERIS) 63-channel scanner data covering the spectral region 0.4 to 2.5 km were analyzed for the Cuprite mining district, Esmeralda and Nye Counties, Nevada. The data were calibrated to reflectance using field spectral measurements. Individual and spatially averaged spectra extracted from the GERIS data were used to identify the minerals alunite, kaolinite, buddingtonite, and hematite by their spectral characterisitcs. An area with reflectance properties similar to zeolite-group minerals was also identified. The images were classified in the spectral domain to produce color-coded image maps of mineral distribution that clearly show the zoned nature of the hydrothermal system. Comparison of the thematic mineral maps with existing geologic and alteration maps demonstrates the utility of imaging spectrometers for producing detailed maps for mineral exploration. Identification of individual minerals and spatial display of the dominant mineralogy using the imaging spectrometer data adds information that can be used in determining the morphology and genetic origin of the district. INTRODUCTION 1'111'1'1'1'1'1'1'1 -ALUNITE LAB SPEClRUM - HE OBJECTIVE OF THIS RESEARCH was both to evaluate the - ----- TM RESAMPLU) ALUNI'W - TGENS and to use the data to develop a better understanding CUPRm OERlS ALUNllE - of the hydrothermal system at Cuprite, Nevada.