Conditional Graphical Models for Protein Structure Prediction
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Protein Identities in Evs Isolated from U87-MG GBM Cells As Determined by NG LC-MS/MS
Protein identities in EVs isolated from U87-MG GBM cells as determined by NG LC-MS/MS. No. Accession Description Σ Coverage Σ# Proteins Σ# Unique Peptides Σ# Peptides Σ# PSMs # AAs MW [kDa] calc. pI 1 A8MS94 Putative golgin subfamily A member 2-like protein 5 OS=Homo sapiens PE=5 SV=2 - [GG2L5_HUMAN] 100 1 1 7 88 110 12,03704523 5,681152344 2 P60660 Myosin light polypeptide 6 OS=Homo sapiens GN=MYL6 PE=1 SV=2 - [MYL6_HUMAN] 100 3 5 17 173 151 16,91913397 4,652832031 3 Q6ZYL4 General transcription factor IIH subunit 5 OS=Homo sapiens GN=GTF2H5 PE=1 SV=1 - [TF2H5_HUMAN] 98,59 1 1 4 13 71 8,048185945 4,652832031 4 P60709 Actin, cytoplasmic 1 OS=Homo sapiens GN=ACTB PE=1 SV=1 - [ACTB_HUMAN] 97,6 5 5 35 917 375 41,70973209 5,478027344 5 P13489 Ribonuclease inhibitor OS=Homo sapiens GN=RNH1 PE=1 SV=2 - [RINI_HUMAN] 96,75 1 12 37 173 461 49,94108966 4,817871094 6 P09382 Galectin-1 OS=Homo sapiens GN=LGALS1 PE=1 SV=2 - [LEG1_HUMAN] 96,3 1 7 14 283 135 14,70620005 5,503417969 7 P60174 Triosephosphate isomerase OS=Homo sapiens GN=TPI1 PE=1 SV=3 - [TPIS_HUMAN] 95,1 3 16 25 375 286 30,77169764 5,922363281 8 P04406 Glyceraldehyde-3-phosphate dehydrogenase OS=Homo sapiens GN=GAPDH PE=1 SV=3 - [G3P_HUMAN] 94,63 2 13 31 509 335 36,03039959 8,455566406 9 Q15185 Prostaglandin E synthase 3 OS=Homo sapiens GN=PTGES3 PE=1 SV=1 - [TEBP_HUMAN] 93,13 1 5 12 74 160 18,68541938 4,538574219 10 P09417 Dihydropteridine reductase OS=Homo sapiens GN=QDPR PE=1 SV=2 - [DHPR_HUMAN] 93,03 1 1 17 69 244 25,77302971 7,371582031 11 P01911 HLA class II histocompatibility antigen, -

The Function of NM23-H1/NME1 and Its Homologs in Major Processes Linked to Metastasis
University of Dundee The Function of NM23-H1/NME1 and Its Homologs in Major Processes Linked to Metastasis Mátyási, Barbara; Farkas, Zsolt; Kopper, László; Sebestyén, Anna; Boissan, Mathieu; Mehta, Anil Published in: Pathology and Oncology Research DOI: 10.1007/s12253-020-00797-0 Publication date: 2020 Licence: CC BY Document Version Publisher's PDF, also known as Version of record Link to publication in Discovery Research Portal Citation for published version (APA): Mátyási, B., Farkas, Z., Kopper, L., Sebestyén, A., Boissan, M., Mehta, A., & Takács-Vellai, K. (2020). The Function of NM23-H1/NME1 and Its Homologs in Major Processes Linked to Metastasis. Pathology and Oncology Research, 26(1), 49-61. https://doi.org/10.1007/s12253-020-00797-0 General rights Copyright and moral rights for the publications made accessible in Discovery Research Portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from Discovery Research Portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain. • You may freely distribute the URL identifying the publication in the public portal. Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your -

Eukaryotic Genome Annotation
Comparative Features of Multicellular Eukaryotic Genomes (2017) (First three statistics from www.ensembl.org; other from original papers) C. elegans A. thaliana D. melanogaster M. musculus H. sapiens Species name Nematode Thale Cress Fruit Fly Mouse Human Size (Mb) 103 136 143 3,482 3,555 # Protein-coding genes 20,362 27,655 13,918 22,598 20,338 (25,498 (13,601 original (30,000 (30,000 original est.) original est.) original est.) est.) Transcripts 58,941 55,157 34,749 131,195 200,310 Gene density (#/kb) 1/5 1/4.5 1/8.8 1/83 1/97 LINE/SINE (%) 0.4 0.5 0.7 27.4 33.6 LTR (%) 0.0 4.8 1.5 9.9 8.6 DNA Elements 5.3 5.1 0.7 0.9 3.1 Total repeats 6.5 10.5 3.1 38.6 46.4 Exons % genome size 27 28.8 24.0 per gene 4.0 5.4 4.1 8.4 8.7 average size (bp) 250 506 Introns % genome size 15.6 average size (bp) 168 Arabidopsis Chromosome Structures Sorghum Whole Genome Details Characterizing the Proteome The Protein World • Sequencing has defined o Many, many proteins • How can we use this data to: o Define genes in new genomes o Look for evolutionarily related genes o Follow evolution of genes ▪ Mixing of domains to create new proteins o Uncover important subsets of genes that ▪ That deep phylogenies • Plants vs. animals • Placental vs. non-placental animals • Monocots vs. dicots plants • Common nomenclature needed o Ensure consistency of interpretations InterPro (http://www.ebi.ac.uk/interpro/) Classification of Protein Families • Intergrated documentation resource for protein super families, families, domains and functional sites o Mitchell AL, Attwood TK, Babbitt PC, et al. -

STACK: a Toolkit for Analysing Β-Helix Proteins
STACK: a toolkit for analysing ¯-helix proteins Master of Science Thesis (20 points) Salvatore Cappadona, Lars Diestelhorst Abstract ¯-helix proteins contain a solenoid fold consisting of repeated coils forming parallel ¯-sheets. Our goal is to formalise the intuitive notion of a ¯-helix in an objective algorithm. Our approach is based on first identifying residues stacks — linear spatial arrangements of residues with similar conformations — and then combining these elementary patterns to form ¯-coils and ¯-helices. Our algorithm has been implemented within STACK, a toolkit for analyzing ¯-helix proteins. STACK distinguishes aromatic, aliphatic and amidic stacks such as the asparagine ladder. Geometrical features are computed and stored in a relational database. These features include the axis of the ¯-helix, the stacks, the cross-sectional shape, the area of the coils and related packing information. An interface between STACK and a molecular visualisation program enables structural features to be highlighted automatically. i Contents 1 Introduction 1 2 Biological Background 2 2.1 Basic Concepts of Protein Structure ....................... 2 2.2 Secondary Structure ................................ 2 2.3 The ¯-Helix Fold .................................. 3 3 Parallel ¯-Helices 6 3.1 Introduction ..................................... 6 3.2 Nomenclature .................................... 6 3.2.1 Parallel ¯-Helix and its ¯-Sheets ..................... 6 3.2.2 Stacks ................................... 8 3.2.3 Coils ..................................... 8 3.2.4 The Core Region .............................. 8 3.3 Description of Known Structures ......................... 8 3.3.1 Helix Handedness .............................. 8 3.3.2 Right-Handed Parallel ¯-Helices ..................... 13 3.3.3 Left-Handed Parallel ¯-Helices ...................... 19 3.4 Amyloidosis .................................... 20 4 The STACK Toolkit 24 4.1 Identification of Structural Elements ....................... 24 4.1.1 Stacks ................................... -

Development and Validation of a Protein-Based Risk Score for Cardiovascular Outcomes Among Patients with Stable Coronary Heart Disease
Supplementary Online Content Ganz P, Heidecker B, Hveem K, et al. Development and validation of a protein-based risk score for cardiovascular outcomes among patients with stable coronary heart disease. JAMA. doi: 10.1001/jama.2016.5951 eTable 1. List of 1130 Proteins Measured by Somalogic’s Modified Aptamer-Based Proteomic Assay eTable 2. Coefficients for Weibull Recalibration Model Applied to 9-Protein Model eFigure 1. Median Protein Levels in Derivation and Validation Cohort eTable 3. Coefficients for the Recalibration Model Applied to Refit Framingham eFigure 2. Calibration Plots for the Refit Framingham Model eTable 4. List of 200 Proteins Associated With the Risk of MI, Stroke, Heart Failure, and Death eFigure 3. Hazard Ratios of Lasso Selected Proteins for Primary End Point of MI, Stroke, Heart Failure, and Death eFigure 4. 9-Protein Prognostic Model Hazard Ratios Adjusted for Framingham Variables eFigure 5. 9-Protein Risk Scores by Event Type This supplementary material has been provided by the authors to give readers additional information about their work. Downloaded From: https://jamanetwork.com/ on 10/02/2021 Supplemental Material Table of Contents 1 Study Design and Data Processing ......................................................................................................... 3 2 Table of 1130 Proteins Measured .......................................................................................................... 4 3 Variable Selection and Statistical Modeling ........................................................................................ -

Calculating the Structure-Based Phylogenetic Relationship
CALCULATING THE STRUCTURE-BASED PHYLOGENETIC RELATIONSHIP OF DISTANTLY RELATED HOMOLOGOUS PROTEINS UTILIZING MAXIMUM LIKELIHOOD STRUCTURAL ALIGNMENT COMBINATORICS AND A NOVEL STRUCTURAL MOLECULAR CLOCK HYPOTHESIS A DISSERTATION IN Molecular Biology and Biochemistry and Cell Biology and Biophysics Presented to the Faculty of the University of Missouri-Kansas City in partial fulfillment of the requirements for the degree Doctor of Philosophy by SCOTT GARRETT FOY B.S., Southwest Baptist University, 2005 B.A., Truman State University, 2007 M.S., University of Missouri-Kansas City, 2009 Kansas City, Missouri 2013 © 2013 SCOTT GARRETT FOY ALL RIGHTS RESERVED CALCULATING THE STRUCTURE-BASED PHYLOGENETIC RELATIONSHIP OF DISTANTLY RELATED HOMOLOGOUS PROTEINS UTILIZING MAXIMUM LIKELIHOOD STRUCTURAL ALIGNMENT COMBINATORICS AND A NOVEL STRUCTURAL MOLECULAR CLOCK HYPOTHESIS Scott Garrett Foy, Candidate for the Doctor of Philosophy Degree University of Missouri-Kansas City, 2013 ABSTRACT Dendrograms establish the evolutionary relationships and homology of species, proteins, or genes. Homology modeling, ligand binding, and pharmaceutical testing all depend upon the homology ascertained by dendrograms. Regardless of the specific algorithm, all dendrograms that ascertain protein evolutionary homology are generated utilizing polypeptide sequences. However, because protein structures superiorly conserve homology and contain more biochemical information than their associated protein sequences, I hypothesize that utilizing the structure of a protein instead -

Assessing the Human Canonical Protein Count[Version 1; Peer Review
F1000Research 2017, 6:448 Last updated: 15 JUL 2020 REVIEW Last rolls of the yoyo: Assessing the human canonical protein count [version 1; peer review: 1 approved, 2 approved with reservations] Christopher Southan IUPHAR/BPS Guide to Pharmacology, Centre for Integrative Physiology, University of Edinburgh, Edinburgh, EH8 9XD, UK First published: 07 Apr 2017, 6:448 Open Peer Review v1 https://doi.org/10.12688/f1000research.11119.1 Latest published: 07 Apr 2017, 6:448 https://doi.org/10.12688/f1000research.11119.1 Reviewer Status Abstract Invited Reviewers In 2004, when the protein estimate from the finished human genome was 1 2 3 only 24,000, the surprise was compounded as reviewed estimates fell to 19,000 by 2014. However, variability in the total canonical protein counts version 1 (i.e. excluding alternative splice forms) of open reading frames (ORFs) in 07 Apr 2017 report report report different annotation portals persists. This work assesses these differences and possible causes. A 16-year analysis of Ensembl and UniProtKB/Swiss-Prot shows convergence to a protein number of ~20,000. The former had shown some yo-yoing, but both have now plateaued. Nine 1 Michael Tress, Spanish National Cancer major annotation portals, reviewed at the beginning of 2017, gave a spread Research Centre (CNIO), Madrid, Spain of counts from 21,819 down to 18,891. The 4-way cross-reference concordance (within UniProt) between Ensembl, Swiss-Prot, Entrez Gene 2 Elspeth A. Bruford , European Molecular and the Human Gene Nomenclature Committee (HGNC) drops to 18,690, Biology Laboratory, Hinxton, UK indicating methodological differences in protein definitions and experimental existence support between sources. -

And Beta-Helical Protein Motifs
Soft Matter Mechanical Unfolding of Alpha- and Beta-helical Protein Motifs Journal: Soft Matter Manuscript ID SM-ART-10-2018-002046.R1 Article Type: Paper Date Submitted by the 28-Nov-2018 Author: Complete List of Authors: DeBenedictis, Elizabeth; Northwestern University Keten, Sinan; Northwestern University, Mechanical Engineering Page 1 of 10 Please doSoft not Matter adjust margins Soft Matter ARTICLE Mechanical Unfolding of Alpha- and Beta-helical Protein Motifs E. P. DeBenedictis and S. Keten* Received 24th September 2018, Alpha helices and beta sheets are the two most common secondary structure motifs in proteins. Beta-helical structures Accepted 00th January 20xx merge features of the two motifs, containing two or three beta-sheet faces connected by loops or turns in a single protein. Beta-helical structures form the basis of proteins with diverse mechanical functions such as bacterial adhesins, phage cell- DOI: 10.1039/x0xx00000x puncture devices, antifreeze proteins, and extracellular matrices. Alpha helices are commonly found in cellular and extracellular matrix components, whereas beta-helices such as curli fibrils are more common as bacterial and biofilm matrix www.rsc.org/ components. It is currently not known whether it may be advantageous to use one helical motif over the other for different structural and mechanical functions. To better understand the mechanical implications of using different helix motifs in networks, here we use Steered Molecular Dynamics (SMD) simulations to mechanically unfold multiple alpha- and beta- helical proteins at constant velocity at the single molecule scale. We focus on the energy dissipated during unfolding as a means of comparison between proteins and work normalized by protein characteristics (initial and final length, # H-bonds, # residues, etc.). -

Introduction to the Local Theory of Curves and Surfaces
Introduction to the Local Theory of Curves and Surfaces Notes of a course for the ICTP-CUI Master of Science in Mathematics Marco Abate, Fabrizio Bianchi (with thanks to Francesca Tovena) (Much more on this subject can be found in [1]) CHAPTER 1 Local theory of curves Elementary geometry gives a fairly accurate and well-established notion of what is a straight line, whereas is somewhat vague about curves in general. Intuitively, the difference between a straight line and a curve is that the former is, well, straight while the latter is curved. But is it possible to measure how curved a curve is, that is, how far it is from being straight? And what, exactly, is a curve? The main goal of this chapter is to answer these questions. After comparing in the first two sections advantages and disadvantages of several ways of giving a formal definition of a curve, in the third section we shall show how Differential Calculus enables us to accurately measure the curvature of a curve. For curves in space, we shall also measure the torsion of a curve, that is, how far a curve is from being contained in a plane, and we shall show how curvature and torsion completely describe a curve in space. 1.1. How to define a curve n What is a curve (in a plane, in space, in R )? Since we are in a mathematical course, rather than in a course about military history of Prussian light cavalry, the only acceptable answer to such a question is a precise definition, identifying exactly the objects that deserve being called curves and those that do not. -
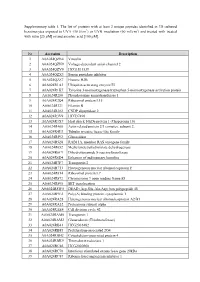
Supplementary Table 1. the List of Proteins with at Least 2 Unique
Supplementary table 1. The list of proteins with at least 2 unique peptides identified in 3D cultured keratinocytes exposed to UVA (30 J/cm2) or UVB irradiation (60 mJ/cm2) and treated with treated with rutin [25 µM] or/and ascorbic acid [100 µM]. Nr Accession Description 1 A0A024QZN4 Vinculin 2 A0A024QZN9 Voltage-dependent anion channel 2 3 A0A024QZV0 HCG1811539 4 A0A024QZX3 Serpin peptidase inhibitor 5 A0A024QZZ7 Histone H2B 6 A0A024R1A3 Ubiquitin-activating enzyme E1 7 A0A024R1K7 Tyrosine 3-monooxygenase/tryptophan 5-monooxygenase activation protein 8 A0A024R280 Phosphoserine aminotransferase 1 9 A0A024R2Q4 Ribosomal protein L15 10 A0A024R321 Filamin B 11 A0A024R382 CNDP dipeptidase 2 12 A0A024R3V9 HCG37498 13 A0A024R3X7 Heat shock 10kDa protein 1 (Chaperonin 10) 14 A0A024R408 Actin related protein 2/3 complex, subunit 2, 15 A0A024R4U3 Tubulin tyrosine ligase-like family 16 A0A024R592 Glucosidase 17 A0A024R5Z8 RAB11A, member RAS oncogene family 18 A0A024R652 Methylenetetrahydrofolate dehydrogenase 19 A0A024R6C9 Dihydrolipoamide S-succinyltransferase 20 A0A024R6D4 Enhancer of rudimentary homolog 21 A0A024R7F7 Transportin 2 22 A0A024R7T3 Heterogeneous nuclear ribonucleoprotein F 23 A0A024R814 Ribosomal protein L7 24 A0A024R872 Chromosome 9 open reading frame 88 25 A0A024R895 SET translocation 26 A0A024R8W0 DEAD (Asp-Glu-Ala-Asp) box polypeptide 48 27 A0A024R9E2 Poly(A) binding protein, cytoplasmic 1 28 A0A024RA28 Heterogeneous nuclear ribonucleoprotein A2/B1 29 A0A024RA52 Proteasome subunit alpha 30 A0A024RAE4 Cell division cycle 42 31 -

Chern-Simons-Higgs Model As a Theory of Protein Molecules
ITEP-TH-12/19 Chern-Simons-Higgs Model as a Theory of Protein Molecules Dmitry Melnikov and Alyson B. F. Neves November 13, 2019 Abstract In this paper we discuss a one-dimensional Abelian Higgs model with Chern-Simons interaction as an effective theory of one-dimensional curves embedded in three-dimensional space. We demonstrate how this effective model is compatible with the geometry of protein molecules. Using standard field theory techniques we analyze phenomenologically interesting static configurations of the model and discuss their stability. This simple model predicts some characteristic relations for the geometry of secondary structure motifs of proteins, and we show how this is consistent with the experimental data. After using the data to universally fix basic local geometric parameters, such as the curvature and torsion of the helical motifs, we are left with a single free parameter. We explain how this parameter controls the abundance and shape of the principal motifs (alpha helices, beta strands and loops connecting them). 1 Introduction Proteins are very complex objects, but in the meantime there is an impressive underlying regularity beyond their structure. This regularity is captured in part by the famous Ramachandran plots that map the correlation of the dihedral (torsion) angles of consecutive bonds in the protein backbone (see for example [1, 2, 3]). The example on figure 1 shows an analogous data of about hundred of proteins, illustrating the localization of the pairs of angles around two regions.1 These two most densely populated regions, labeled α and β, correspond to the most common secondary structure elements in proteins: (right) alpha helices and beta strands. -

Computational Genomics
COMPUTATIONAL GENOMICS: GROUP MEMBERS: Anshul Kundaje (EE) [email protected] Daita Domnica Nicolae (Bio) [email protected] Deniz Sarioz (CS) [email protected] Joseph Gagliano (CS) [email protected] Predicting the Beta-helix fold from Protein sequence data Abstract: This project involves the study and implementation of Betawrap, an algorithm used to predict Beta-helix supersecondary structural motifs using protein sequence data. We begin with a biochemical view of proteins and their structural features. This is followed by a general discussion of the various methods of protein structural prediction. A structural viewpoint of the Beta-Helix is highlighted followed by a detailed discussion of Betawrap. We include the design and implementation details alongside. PERL was the programming language used for the implementation. The alpha helical filter was implemented with the help of pre-existing software known as Pred2ary. The implementation was run on a positive and negative test set, a total of 59 proteins. These tests sets were generated from the SCOP database by checking predictions made by the original Betawrap software and by directly looking at the structures in the PDB. Our program can be downloaded from betawrap.tar.gz. The archive contains a readme with necessary instructions. The program has been commented extensively. Some debugging statements have also be left as comments. The predictions made by our program are very accurate and we had a only 2 misclassifications in a set of 59 proteins. Basic Biochemistry of Protein Structure: Proteins are polymers of 20 different amino acids joined by peptide bonds. At physiological temperatures in aqueous solution, the polypeptide chains of proteins fold into a structure that in most cases is globular.