Q Skills Review Dr
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lesson 1: Length English Vs
Lesson 1: Length English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer B. 1 yard or 1 meter C. 1 inch or 1 centimeter English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers 1 yard = 0.9444 meters English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers 1 inch = 2.54 centimeters 1 yard = 0.9444 meters Metric Units The basic unit of length in the metric system in the meter and is represented by a lowercase m. Standard: The distance traveled by light in absolute vacuum in 1∕299,792,458 of a second. Metric Units 1 Kilometer (km) = 1000 meters 1 Meter = 100 Centimeters (cm) 1 Meter = 1000 Millimeters (mm) Which is larger? A. 1 meter or 105 centimeters C. 12 centimeters or 102 millimeters B. 4 kilometers or 4400 meters D. 1200 millimeters or 1 meter Measuring Length How many millimeters are in 1 centimeter? 1 centimeter = 10 millimeters What is the length of the line in centimeters? _______cm What is the length of the line in millimeters? _______mm What is the length of the line to the nearest centimeter? ________cm HINT: Round to the nearest centimeter – no decimals. -

Download Metric Conversion Factors
Metric Conversion Factors Imperial Units Factor Metric Units Imperial Units Factor Metric Units LENGTH oz./acre 70 g/ha inches 2.5 centimeters (cm) lb./acre 1.12 kg/ha feet 30 centimeters (cm) bu./acre 0.9 hL/ha feet 0.3 meters (m) tons/acre 2.24 t/ha yards 0.9 meters (m) fl.oz./acre 70 mL/ha miles 1.6 kilometers (km) pt./acre 1.4 L/ha qt./acre 2.8 L/ha AREA gal./acre 11.2 L/ha square inches 6.5 square centimeters (cm2) gal./acre (US) 9.35 L/ha square feet 0.09 square meters (m2) plants/acre 2.47 plants/ha acres 0.40 hectacres (ha) oz./gal. 6.2 mL/L lb/gal. .01 kg/L VOLUME oz./sq.ft. 305 g/m2 cubic inches 16 cubic centimeters (cm3) lb./sq.ft. 4.9 kg/m2 cubic feet 0.03 cubic meters (m3) oz./ft.row 93 g/m row cubic yards 0.8 cubic meters (m3) lb./ft.row 1.5 kg/m row fluid ounces 28 milliliters (mL) ft./sec. 0.3 m/s pints 0.57 liters (L) m.p.h. 1.6 km/h quarts 1.1 liters (L) p.s.i. 6.9 kPa gallons (imperial) 4.5 liters (L) gallons (US) 3.75 liters (L) To convert from imperial to metric, multiply by the conversion factor. bushels 0.36 hectoliters (hL) For example: 10 inches x 2.5 = 25 centimeters To convert from metric to imperial, divide by the conversion factor. -

Imperial Units
Imperial units From Wikipedia, the free encyclopedia Jump to: navigation, search This article is about the post-1824 measures used in the British Empire and countries in the British sphere of influence. For the units used in England before 1824, see English units. For the system of weight, see Avoirdupois. For United States customary units, see Customary units . Imperial units or the imperial system is a system of units, first defined in the British Weights and Measures Act of 1824, later refined (until 1959) and reduced. The system came into official use across the British Empire. By the late 20th century most nations of the former empire had officially adopted the metric system as their main system of measurement. The former Weights and Measures office in Seven Sisters, London. Contents [hide] • 1 Relation to other systems • 2 Units ○ 2.1 Length ○ 2.2 Area ○ 2.3 Volume 2.3.1 British apothecaries ' volume measures ○ 2.4 Mass • 3 Current use of imperial units ○ 3.1 United Kingdom ○ 3.2 Canada ○ 3.3 Australia ○ 3.4 Republic of Ireland ○ 3.5 Other countries • 4 See also • 5 References • 6 External links [edit] Relation to other systems The imperial system is one of many systems of English or foot-pound-second units, so named because of the base units of length, mass and time. Although most of the units are defined in more than one system, some subsidiary units were used to a much greater extent, or for different purposes, in one area rather than the other. The distinctions between these systems are often not drawn precisely. -

The International System of Units (SI) - Conversion Factors For
NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v -

Appendix C – General Tables of Units of Measurement
Handbook 44 – 2014 Appendix C – General Tables of Units of Measurement Table of Contents Appendix C. General Tables of Units of Measurement ........................................................ C-3 1. Tables of Metric Units of Measurement ..................................................................................................... C-3 Units of Length ............................................................................................................................................... C-3 Units of Area .................................................................................................................................................. C-3 Units of Liquid Volume .................................................................................................................................. C-4 Units of Volume ............................................................................................................................................. C-4 Units of Mass .................................................................................................................................................. C-4 2. Tables of U.S. Units of Measurement ......................................................................................................... C-4 Units of Length ............................................................................................................................................... C-4 Units of Area ................................................................................................................................................. -

Measurements and Conversions
For your review, this is the first five pages of Chapter 12 of The Original Encyclopizza. To return to prior page, use your Back button. ~ To get more info on this book, go to: http://correllconcepts.com/Encyclopizza/_home_encyclopizza.htm To order this book, go to: https://www.amazon.com/dp/B00XK0Q4V6 – Chapter 12 – Measurements and Conversions ecause this website was created by an American company, lengths, weights, temperatures, and liquid volume measure- Bments are given in inches, pounds and ounces, degrees Fahren- heit, and quarts and cups (U.S. version). If you deal in another measurement system, this chapter will help make the conversion. Abbreviations U.S. Metric oz = ounce g = gram (also gm) lb = pound kg = kilogram (kilo) t = teaspoon (also tsp) ml = milliliter T = tablespoon (also tbsp) cl = centiliter c = cup l = liter (also L) pt = pint mm = millimeter qt = quart cm = centimeter gal = gallon m = meter in = inches (also " ) C = Celsius (Centigrade) ft = feet yd = yard F = Fahrenheit 437 438 Chapter 12 Liquid Volume Equivalents For liquid volume measurements (U.S. version), here’s two charts of equivalent amounts that can be handy when reducing or expanding recipes. Small “t” = teaspoon. Capital “T” = tablespoon. VOLUME-TO-VOLUME VOLUME-TO-WEIGHT* 3 t = 1 T 1/4 t = 1/24 fluid ounce 16 T = 1 c 1/2 t = 1/12 fl oz 2 c = 1 pt 1 t = 1/6 fl oz 2 pt = 1 qt 1 T = 1/2 fl oz (2T = 1 fl oz) 4 qt = 1 gal 1 c = 8 fl oz 1 pt = 16 fl oz 1 qt = 32 fl oz 1 gal = 128 fl oz * U.S. -
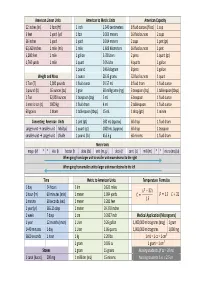
Conversion Chart Revised
American Linear Units American to Metric Units American Capacity 12 inches (in) 1 foot (ft) 1 inch 2.540 centimeters 8 fluid ounces (fl oz) 1 cup 3 feet 1 yard (yd) 1 foot 0.305 meters 16 fluid ounces 2 cups 36 inches 1 yard 1 yard 0.914 meters 2 cups 1 pint (pt) 63,360 inches 1 mile (mi) 1 mile 1.609 kilometers 16 fluid ounces 1 pint 5,280 feet 1 mile 1 gallon 3.78 Liters 2 pints 1 quart (qt) 1,760 yards 1 mile 1 quart 0.95 Liter 4 quarts 1 gallon 1 pound 0.45 kilogram 8 pints 1 gallon Weight and Mass 1 ounce 28.35 grams 32 fluid ounces 1 quart 1 T on (T) 2,000 pounds 1 fluid ounce 29.57 mL 8 fluid dram 1 fluid ounce 1 pound (lb) 16 ounces (oz) 1 grain 60 milligrams (mg) 3 teaspoon (tsp) 1 tablespoon (tbsp) 1 Ton 32,000 ounces 1 teaspoon (tsp) 5 mL 6 teaspoon 1 fluid ounce 1 metric ton (t) 1000 kg 1 fluid dram 4 mL 2 tablespoon 1 fluid ounce 60 grains 1 dram 1 tablespoon (tbsp) 15 mL 1 drop (gtt) 1 minim Converting American Units 1 pint (pt) 500 mL (approx) 60 drop 1 fluid dram Larger unit → smaller unit Multiply 1 quart (qt) 1000 mL (approx) 60 drop 1 teaspoon smaller unit → Larger unit Divide 1 pound (lb) 453.6 g 60 minims 1 fluid dram Metric Units mega (M) * * kilo (k) hector (h) deka (da) unit (m, g, L) deci (d) centi (c) milli (m) * * micro (mc) (u) When going from larger unit to smaller unit move decimal to the right cimal to the left When going from smaller unit to larger unit move de Time Metric to American Units Temperature Formulas 1 day 24 hours 1 km 0.621 miles ʚ̀ Ǝ 32 ʛ 1 hour (hr) 60 minutes (min) 1 meter 1.094 yards ̽ -

CHAPTER 6: MEASUREMENTS Contents
College Prep Essential Math Chapter 6: Measurements CHAPTER 6: MEASUREMENTS Chapter Objectives By the end of this chapter, students should be able to: Identify terms used in measurement in both metric and U.S. customary systems Distinguish between 1, 2, and 3 dimensional measures. Convert U.S. customary unit measures. Convert between U.S. and metric systems. Solve applications of unit measurements. Contents CHAPTER 6: MEASUREMENTS .................................................................................... 1 SECTION 6.1 MEASUREMENT .................................................................................. 2 A. U.S. CUSTOMARY SYSTEM ......................................................................... 2 I. Weight ............................................................................................................. 2 II. Length.......................................................................................................... 3 III. Area ............................................................................................................. 5 IV. Volume ........................................................................................................ 6 B. METRIC SYSTEM .......................................................................................... 9 I. Weight ............................................................................................................. 9 II. Length......................................................................................................... -

Common Weights and Measures
Common Weights and Measures Length Metric System 1 millimeter = 1/1,000 meter 1 centimeter = 1/100 meter 1 decimeter = 1/10 meter 1 meter (basic unit of length) 1 dekameter = 10 meters 1 kilometer = 1,000 meters American and British Units 1 inch = 1/36 yard = 1/12 foot 1 foot = 1/3 yard 1 yard (basic unit of length) 1 rod = 5 1/2 yards 1 furlong = 220 yards = 40 rods 1 mile = 1,760 yards = 5,280 feet 1 fathom = 6 feet 1 nautical mile = 6,076.1 feet Conversion Factors 1 centimeter = 0.39 inch 1 inch = 2.54 centimeters 1 meter = 39.37 inches 1 foot = 0.305 meter 1 meter = 3.28 feet 1 yard = 0.914 meter 1 meter = 1.094 yards 1 kilometer = 0.62 mile 1 mile = 1.609 kilometers Area Metric System 1 square centimeter = 1/10,000 square meter 1 square decimeter = 1/100 square meter 1 square meter (basic unit of area) 1 are = 100 square meters 1 hectare = 10,000 square meters = 100 ares 1 square kilometer = 1,000,000 square meters American and British Units 1 square inch = 1/1,296 square yard = 1/144 square foot 1 square foot = 1/9 square yard 1 square yard (basic unit of area) 1 square rod = 30 1/4 square yards 1 acre = 4,840 square yards = 160 square rods 1 square mile = 3,097,600 square yards = 640 acres Conversion Factors 1 square centimeter = 0.155 square inch 1 square inch = 6.45 square centimeters 1 acre = 0.405 hectare 1 hectare = 2.47 acres 1 square kilometer = 0.386 square mile 1 square mile = 2.59 square kilometers Volume and Capacity (Liquid and Dry) Metric System 1 cubic centimeter = 1/1,000,000 cubic meter 1 cubic decimeter = 1/1,000 cubic meter 1 cubic meter = 1 stere (basic unit of volume) 1 milliliter = 1/1,000 liter = 1 cubic centimeter 1 centiliter = 1/100 liter 1 deciliter = 1/10 liter 1 liter = 1 cubic decimeter (basic unit of capacity) 1 dekaliter = 10 liters 1 hectoliter = 100 liters = 1/10 cubic meter American and British Units 1 cubic inch = 1/46,656 cubic yard = 1/1,728 cubic foot 1 cubic foot = 1/27 cubic yard 1 cubic yard (basic unit of volume) 1 U.S. -

Measurements and Conversions
CH 5 MEASUREMENTS AND CONVERSIONS LEARNING OBJECTIVES INTRODUCTION List the metric equivalents of 1 fluid ounce, During and after the Renaissance, the study of science and 1 tablespoonful, and 1 teaspoonful. medicine began in earnest. At that point in history, no consistent, international system of weights and measures List the metric equivalent of 1 pound, 1 ounce, existed. Measurements of mass (usually referred to as and 1 grain. weight) were based on a commonly weighed material, such Convert a patient’s weight in pounds to as a grain of wheat or a penny. Different systems of measure- kilograms or in kilograms to pounds. ments were used for different applications. For example, Explain why it is important for technicians to be people who worked in trades such as carpentry or smithery completely comfortable using and converting used a different system of measurement than jewelers or to the metric system. apothecaries. An apothecary was a member of the healing arts who was the predecessor of the modern pharmacist Use dimensional analysis to convert between units. and a specialist in the preparation of medicines and reme- dies. Apothecaries dispensed remedies, performed surgery, and assisted in childbirth. To prepare remedies consistently, OUTLINE apothecaries needed a systematic method for weighing and measuring ingredients. INTRODUCTION The apothecary system of weights and measures was related to the Roman system of measurement. This system HOUSEHOLD AND AVOIRDUPOIS WEIGHTS was based on the grain (gr) as a measurement of weight and AND MEASURES the fluid ounce as a measurement of volume. There are some Units of weight and volume similarities among apothecary measurements, common Measuring doses accurately household measurements, and avoirdupois measurements Solving problems using household measurements (the system of weights and measures historically used in the United States and Great Britain) but also some significant CONVERTING BETWEEN SYSTEMS OF differences. -

Appendix B – Units and Systems of Measurement
Handbook 44 – 2011 Appendix B – Units and Systems of Measurement Table of Contents Appendix B. Units and Systems of Measurement Their Origin, Development, and Present Status .................................................................................................... B3 1. Introduction ................................................................................................................................................... B3 2. Units and Systems of Measurement ............................................................................................................. B3 2.1. Origin and Early History of Units and Standards. ............................................................................... B3 2.1.1. General Survey of Early History of Measurement Systems. ................................................. B3 2.1.2. Origin and Development of Some Common Customary Units. ............................................ B4 2.2. The Metric System. .............................................................................................................................. B5 2.2.1. Definition, Origin, and Development. ................................................................................... B5 2.2.2. International System of Units. ............................................................................................... B6 2.2.3. Units and Standards of the Metric System. ........................................................................... B6 2.3. British and United States Systems of Measurement. -
Milestone's Labeled Rate Is 3 to 5 Fluid Ounces Per Acre For
Milestone’s labeled rate is 3 to 5 fluid ounces per acre for Yellow starthistle and cannot exceed 7 ounces per acre per year. Milestone can be applied up to water’s edge, but cannot drift into any waterbody. Transline’s labeled rate is 4 to 10.5 fluid ounces per acre for Yellow starthistle and cannot exceed 10.5 ounces per acre per year. A non-ionic surfactant may be added at 1 to 2 quarts per 100 gallons of spray mixture to improve uptake of Milestone/Transline by the plant. To figure out how much Milestone/Transline to put in your sprayer you must first calculate your spray volume and application rate. Follow these steps to calibrate your sprayer and thereby figure out your spray volume and application rate: Step 1: Clean your sprayer and nozzle, then fill the tank with clean water. Check to make sure that the nozzle is producing a uniform spray. If not, adjust and/or re-clean the nozzle. Step 2: Measure an area 18.5 feet by 18.5 feet in or near the terrain where you’ll be spraying. Step 3: Time the number of seconds it takes to spray the measured area uniformly with water using gentle side to side sweeping motions. Record the number of seconds required to spray the area. REPEAT THIS STEP at least one more time and take an average of all the times. Step 4: Spray into a container for the average time calculated in Step 3. Step 5: Measure the number of fluid ounces of water in the bucket.