Guidelines for Writing Formulae
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

End-Of-Line Hyphenation of Chemical Names (IUPAC Provisional
Pure Appl. Chem. 2020; aop IUPAC Recommendations Albert J. Dijkstra*, Karl-Heinz Hellwich, Richard M. Hartshorn, Jan Reedijk and Erik Szabó End-of-line hyphenation of chemical names (IUPAC Provisional Recommendations) https://doi.org/10.1515/pac-2019-1005 Received October 16, 2019; accepted January 21, 2020 Abstract: Chemical names and in particular systematic chemical names can be so long that, when a manu- script is printed, they have to be hyphenated/divided at the end of a line. Many systematic names already contain hyphens, but sometimes not in a suitable division position. In some cases, using these hyphens as end-of-line divisions can lead to illogical divisions in print, as can also happen when hyphens are added arbi- trarily without considering the ‘chemical’ context. The present document provides recommendations and guidelines for authors of chemical manuscripts, their publishers and editors, on where to divide chemical names at the end of a line and instructions on how to avoid these names being divided at illogical places as often suggested by desk dictionaries. Instead, readability and chemical sense should prevail when authors insert optional hyphens. Accordingly, the software used to convert electronic manuscripts to print can now be programmed to avoid illogical end-of-line hyphenation and thereby save the author much time and annoy- ance when proofreading. The recommendations also allow readers of the printed article to determine which end-of-line hyphens are an integral part of the name and should not be deleted when ‘undividing’ the name. These recommendations may also prove useful in languages other than English. -
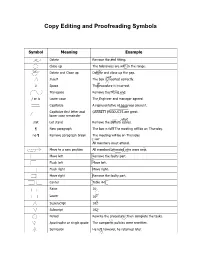
Copy Editing and Proofreading Symbols
Copy Editing and Proofreading Symbols Symbol Meaning Example Delete Remove the end fitting. Close up The tolerances are with in the range. Delete and Close up Deltete and close up the gap. not Insert The box is inserted correctly. # # Space Theprocedure is incorrect. Transpose Remove the fitting end. / or lc Lower case The Engineer and manager agreed. Capitalize A representative of nasa was present. Capitalize first letter and GARRETT PRODUCTS are great. lower case remainder stet stet Let stand Remove the battery cables. ¶ New paragraph The box is full. The meeting will be on Thursday. no ¶ Remove paragraph break The meeting will be on Thursday. no All members must attend. Move to a new position All members attended who were new. Move left Remove the faulty part. Flush left Move left. Flush right Move right. Move right Remove the faulty part. Center Table 4-1 Raise 162 Lower 162 Superscript 162 Subscript 162 . Period Rewrite the procedure. Then complete the tasks. ‘ ‘ Apostrophe or single quote The companys policies were rewritten. ; Semicolon He left however, he returned later. ; Symbol Meaning Example Colon There were three items nuts, bolts, and screws. : : , Comma Apply pressure to the first second and third bolts. , , -| Hyphen A valuable byproduct was created. sp Spell out The info was incorrect. sp Abbreviate The part was twelve feet long. || or = Align Personnel Facilities Equipment __________ Underscore The part was listed under Electrical. Run in with previous line He rewrote the pages and went home. Em dash It was the beginning so I thought. En dash The value is 120 408. -

Classifying Type Thunder Graphics Training • Type Workshop Typeface Groups
Classifying Type Thunder Graphics Training • Type Workshop Typeface Groups Cla sifying Type Typeface Groups The typefaces you choose can make or break a layout or design because they set the tone of the message.Choosing The the more right you font know for the about job is type, an important the better design your decision.type choices There will are be. so many different fonts available for the computer that it would be almost impossible to learn the names of every one. However, manys typefaces share similar qualities. Typographers classify fonts into groups to help Typographers classify type into groups to help remember the different kinds. Often, a font from within oneremember group can the be different substituted kinds. for Often, one nota font available from within to achieve one group the samecan be effect. substituted Different for anothertypographers usewhen different not available groupings. to achieve The classifi the samecation effect. system Different used by typographers Thunder Graphics use different includes groups. seven The major groups.classification system used byStevenson includes seven major groups. Use the Right arrow key to move to the next page. • Use the Left arrow key to move back a page. Use the key combination, Command (⌘) + Q to quit the presentation. Thunder Graphics Training • Type Workshop Typeface Groups ����������������������� ��������������������������������������������������������������������������������� ���������������������������������������������������������������������������� ������������������������������������������������������������������������������ -

I. In-Text Citations in Turabian-Style Papers, Superscript Numbers
MAX Center Writing References Turabian Style I. In-Text Citations In Turabian-style papers, superscript numbers (1) are placed at the end of sentences in which a source is used (quotations, paraphrasing, or any other attribution). The source of the citation is then cited in a correspondingly numbered note which provides extended information. These notes can appear as footnotes at the bottom of the page or endnotes in a list at the end of the paper. In most cases, you will also list sources at the end of the paper in a bibliography. The format for these notes is different from the format of bibliography entries. Superscript numbers should appear at the end of the cited material after all punctuation marks, except when the note refers to material before a dash, in which case the superscript should appear after it. Don’t use more than one reference number at a time if a sentence cites multiple sources—instead, use one number and include all citations in a single note. II. Foot- and Endnotes If you choose to use Endnotes instead of footnotes, they should appear on a separate page entitled Notes. Both footnotes and endnotes are formatted as follows: 1. Single Author or Editor Note Number. Author’s (or Editor’s) First and Last Names, Title of Book: Subtitle of Book (Place of Publication: Publisher’s Name, Date of Publication), XX-XX. 2. Multiple Authors Note Number. Author #1’s First and Last Names and Author #2’s First and Last Names, Title of Book: Subtitle of Book (Place of Publication: Publisher’s Name, Date of Publication), XX-XX. -

AIX Globalization
AIX Version 7.1 AIX globalization IBM Note Before using this information and the product it supports, read the information in “Notices” on page 233 . This edition applies to AIX Version 7.1 and to all subsequent releases and modifications until otherwise indicated in new editions. © Copyright International Business Machines Corporation 2010, 2018. US Government Users Restricted Rights – Use, duplication or disclosure restricted by GSA ADP Schedule Contract with IBM Corp. Contents About this document............................................................................................vii Highlighting.................................................................................................................................................vii Case-sensitivity in AIX................................................................................................................................vii ISO 9000.....................................................................................................................................................vii AIX globalization...................................................................................................1 What's new...................................................................................................................................................1 Separation of messages from programs..................................................................................................... 1 Conversion between code sets............................................................................................................. -

PCL PS Math Symbol Set Page 1 of 4 PCL PS Math Symbol Set
PCL PS Math Symbol Set Page 1 of 4 PCL PS Math Symbol Set PCL Symbol Set: 5M Unicode glyph correspondence tables. Contact:[email protected] http://pcl.to $20 U0020 Space -- -- -- -- $21 U0021 Ê Exclamation mark -- -- -- -- $22 U2200 Ë For all -- -- -- -- $23 U0023 Ì Number sign -- -- -- -- $24 U2203 Í There exists -- -- -- -- $25 U0025 Î Percent sign -- -- -- -- $26 U0026 Ï Ampersand -- -- -- -- $27 U220B & Contains as member -- -- -- -- $28 U0028 ' Left parenthesis -- -- -- -- $29 U0029 ( Right parenthesis -- -- -- -- $2A U2217 ) Asterisk operator -- -- -- -- $2B U002B * Plus sign -- -- -- -- $2C U002C + Comma -- -- -- -- $2D U2212 , Minus sign -- -- -- -- $2E U002E - Full stop -- -- -- -- $2F U002F . Solidus -- -- -- -- $30 U0030 / Digit zero -- -- -- -- $31 U0031 0 Digit one $A1 U03D2 1 Greek upsilon with hook symbol $32 U0032 2 Digit two $A2 U2032 3 Prime $33 U0033 4 Digit three $A3 U2264 5 Less-than or equal to $34 U0034 6 Digit four $A4 U002F . Division slash $35 U0035 7 Digit five $A5 U221E 8 Infinity $36 U0036 9 Digit six $A6 U0192 : Latin small letter f with hook http://www.pclviewer.com (c) RedTitan Technology 2005 PCL PS Math Symbol Set Page 2 of 4 $37 U0037 ; Digit seven $A7 U2663 < Black club suit $38 U0038 = Digit eight $A8 U2666 > Black diamond suit $39 U0039 ? Digit nine $A9 U2665 ê Black heart suit $3A U003A A Colon $AA U2660 B Black spade suit $3B U003B C Semicolon $AB U2194 D Left right arrow $3C U003C E Less-than sign $AC U2190 F Leftwards arrow $3D U003D G Equals sign $AD U2191 H Upwards arrow $3E U003E I Greater-than -

Proper Listing of Scientific and Common Plant Names In
PROPER USAGE OF PLANT NAMES IN PUBLICATIONS A Guide for Writers and Editors Kathy Musial, Huntington Botanical Gardens, August 2017 Scientific names (also known as “Latin names”, “botanical names”) A unit of biological classification is called a “taxon” (plural, “taxa”). This is defined as a taxonomic group of any rank, e.g. genus, species, subspecies, variety. To allow scientists and others to clearly communicate with each other, taxa have names consisting of Latin words. These words may be derived from languages other than Latin, in which case they are referred to as “latinized”. A species name consists of two words: the genus name followed by a second name (called the specific epithet) unique to that species; e.g. Hedera helix. Once the name has been mentioned in text, the genus name may be abbreviated in any immediately subsequent listings of the same species, or other species of the same genus, e.g. Hedera helix, H. canariensis. The first letter of the genus name is always upper case and the first letter of the specific epithet is always lower case. Latin genus and species names should always be italicized when they appear in text that is in roman type; conversely, these Latin names should be in roman type when they appear in italicized text. Names of suprageneric taxa (above the genus level, e.g. families, Asteraceae, etc.), are never italicized when they appear in roman text. The first letter of these names is always upper case. Subspecific taxa (subspecies, variety, forma) have a third epithet that is always separated from the specific epithet by the rank designation “var.”, “ssp.” or “subsp.”, or “forma” (sometimes abbreviated as “f.”); e.g. -

List of Approved Special Characters
List of Approved Special Characters The following list represents the Graduate Division's approved character list for display of dissertation titles in the Hooding Booklet. Please note these characters will not display when your dissertation is published on ProQuest's site. To insert a special character, simply hold the ALT key on your keyboard and enter in the corresponding code. This is only for entering in a special character for your title or your name. The abstract section has different requirements. See abstract for more details. Special Character Alt+ Description 0032 Space ! 0033 Exclamation mark '" 0034 Double quotes (or speech marks) # 0035 Number $ 0036 Dollar % 0037 Procenttecken & 0038 Ampersand '' 0039 Single quote ( 0040 Open parenthesis (or open bracket) ) 0041 Close parenthesis (or close bracket) * 0042 Asterisk + 0043 Plus , 0044 Comma ‐ 0045 Hyphen . 0046 Period, dot or full stop / 0047 Slash or divide 0 0048 Zero 1 0049 One 2 0050 Two 3 0051 Three 4 0052 Four 5 0053 Five 6 0054 Six 7 0055 Seven 8 0056 Eight 9 0057 Nine : 0058 Colon ; 0059 Semicolon < 0060 Less than (or open angled bracket) = 0061 Equals > 0062 Greater than (or close angled bracket) ? 0063 Question mark @ 0064 At symbol A 0065 Uppercase A B 0066 Uppercase B C 0067 Uppercase C D 0068 Uppercase D E 0069 Uppercase E List of Approved Special Characters F 0070 Uppercase F G 0071 Uppercase G H 0072 Uppercase H I 0073 Uppercase I J 0074 Uppercase J K 0075 Uppercase K L 0076 Uppercase L M 0077 Uppercase M N 0078 Uppercase N O 0079 Uppercase O P 0080 Uppercase -

Top Ten Tips for Effective Punctuation in Legal Writing
TIPS FOR EFFECTIVE PUNCTUATION IN LEGAL WRITING* © 2005 The Writing Center at GULC. All Rights Reserved. Punctuation can be either your friend or your enemy. A typical reader will seldom notice good punctuation (though some readers do appreciate truly excellent punctuation). However, problematic punctuation will stand out to your reader and ultimately damage your credibility as a writer. The tips below are intended to help you reap the benefits of sophisticated punctuation while avoiding common pitfalls. But remember, if a sentence presents a particularly thorny punctuation problem, you may want to consider rephrasing for greater clarity. This handout addresses the following topics: THE COMMA (,)........................................................................................................................... 2 PUNCTUATING QUOTATIONS ................................................................................................. 4 THE ELLIPSIS (. .) ..................................................................................................................... 4 THE APOSTROPHE (’) ................................................................................................................ 7 THE HYPHEN (-).......................................................................................................................... 8 THE DASH (—) .......................................................................................................................... 10 THE SEMICOLON (;) ................................................................................................................ -

Pageflex Character Entitiesa
Pageflex Character EntitiesA A list of all special character entities recognized by Pageflex products n 1 Pageflex Character Entities The NuDoc composition engine inside Pageflex applications recognizes many special entities beginning with the “&” symbol and end with the “;” symbol. Each represents a particular Unicode character in XML content. For information on entity definitions, look up their Unicode identifiers in The Unicode Standard book. This appendix contains two tables: the first lists character entities by name, the second by Unicode identifier. Character Entities by Entity Name This section lists character entities by entity name. You must precede the entity name by “&” and follow it by “;” for NuDoc to recognize the name (e.g., “á”). Note: Space and break characters do not have visible entity symbols. The entity symbol column for these characters is purposely blank. Entity Entity Name Unicode Unicode Name Symbol aacute 0x00E1 á LATIN SMALL LETTER A WITH ACUTE Aacute 0x00C1 Á LATIN CAPITAL LETTER A WITH ACUTE acirc 0x00E2 â LATIN SMALL LETTER A WITH CIRCUMFLEX Acirc 0x00C2 Â LATIN CAPITAL LETTER A WITH CIRCUMFLEX acute 0x00B4 ´ ACUTE ACCENT aelig 0x00E6 æ LATIN SMALL LIGATURE AE AElig 0x00C6 Æ LATIN CAPITAL LIGATURE AE agrave 0x00E0 à LATIN SMALL LETTER A WITH GRAVE Agrave 0x00C0 À LATIN CAPITAL LETTER A WITH GRAVE ape 0x2248 ALMOST EQUAL TO aring 0x00E5 å LATIN SMALL LETTER A WITH RING ABOVE n 2 Entity Entity Name Unicode Unicode Name Symbol Aring 0x00C5 Å LATIN CAPITAL LETTER A WITH RING ABOVE atilde 0x00E3 ã LATIN SMALL LETTER A WITH TILDE Atilde 0x00C3 Ã LATIN CAPITAL LETTER A WITH TILDE auml 0x00E4 ä LATIN SMALL LETTER A WITH DIERESIS Auml 0x00C4 Ä LATIN CAPITAL LETTER A WITH DIERESIS bangbang 0x203C DOUBLE EXCLAMATION MARK br 0x2028 LINE SEPERATOR (I.E. -

Revised Proposal to Encode a Punctuation Mark "Double Hyphen"
Universal Multiple-Octet Coded Character Set International Organization for Standardization Organisation Internationale de Normalisation Международная организация по стандартизации Doc Type: Working Group Document Title: Revised Proposal to encode a punctuation mark "Double Hyphen" Source: German NB Status: National Body Contribution Action: For consideration by JTC1/SC2/WG2 and UTC Date: 2011-01-17 Replaces: N3917 = L2/10-361, L2/10-162 Dashes and Hyphens A U+2E4E DOUBLE HYPHEN → 2010 hyphen → 2E17 double oblique hyphen → 003D equals sign → A78A modifier letter short equals sign · used in transcription of old German prints and handwritings · used in some non-standard punctuation · not intended for standard hyphens where the duplication is only a font variant Properties: 2E4E;DOUBLE HYPHEN;Pd;0;ON;;;;;N;;;;; Entry in LineBreak.TXT: 2E4E;BA # DOUBLE HYPHEN 1. Introduction The "ordinary" hyphen, which is representable by U+002D HYPHEN-MINUS or U+2010 HYPHEN, usually is displayed by a single short horizontal dash, but has a considerable glyph variation: it can be slanted to oblique or doubled (stacked) according to the used font. For instance, in Fraktur (Blackletter) fonts, it commonly is represented by two stacked short oblique dashes. However, in certain applications, double hyphens (consisting of two stacked short dashes) are used as characters with semantics deviating from the "ordinary" hyphen, e.g. to represent a definite unit in transliteration. For such a special application, in this case for transliteration of Coptic, U+2E17 DOUBLE OBLIQUE HYPHEN was encoded ([1], example on p. 9). However, there are other applications where the double hyphen is usually not oblique. For such applications, a "DOUBLE HYPHEN" is proposed here, which consists of two stacked short dashes which usually are horizontal. -

Typography for Scientific and Business Documents
Version 1.8 Typography for Scientific and Business Documents George Yefchak Agilent Laboratories What’s the Big Deal? This paper is about typography. But first, I digress… inch marks, so you’ll probably get to enter those manually anyway.† Nothing is perfect…) Most of us agree that the use of correct grammar — or at In American English, punctuation marks are usually placed least something approaching it — is important in our printed before closing quotes rather than after them (e.g. She said documents. Of course “printed documents” refers not just to “No!”). But don’t do this if it would confuse the message words printed on paper these days, but also to things distrib- (e.g. Did she say “no!”?). Careful placement of periods and uted by slide and overhead projection, electronic broadcast- commas is particularly important when user input to ing, the web, etc. When we write something down, we computers is described: usually make our words conform to accepted rules of For username, type “john.” Wrong grammar for a selfish reason: we want the reader to think we For username, type “john”. ok know what we’re doing! But grammar has a more fundamen- tal purpose. By following the accepted rules, we help assure For username, type john . Even better, if font usage that the reader understands our message. is explained If you don’t get into the spirit of things, you might look at Dashes typography as just another set of rules to follow. But good The three characters commonly referred to as “dashes” are: typography is important, because it serves the same two purposes as good grammar.