The Crystal Structure of Stibnite a Redetermination of Atomic Positions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Stibnite Gold Project
STIBNITE GOLD PROJECT PAYETTE & BOISE NATIONAL FORESTS INTERMOUNTAIN REGION August 22, 2018 STIBNITE MINING DISTRICT, PAYETTE NATIONAL FOREST, KRASSEL RANGER DISTRICT Regarding Locatable Minerals , 36 CFR 228, Subpart A: requires the Forest Service to: "Where conflicting interests Respond to a mining plan, evaluate that plan must be reconciled, the Consider requirements to minimize adverse effects to the extent feasible question shall always be Comply with applicable laws, regulations and answered from the stand- standards for environmental protection point of the greatest good of Assure appropriate reclamation Further respond by following National Environmental the greatest number in the Policy Act (NEPA) processes. long run." - James Wilson, Secretary Per 36 CFR 228.4, the Forest Service is required to take of Agriculture, 1905 in a letter to Gifford action to ensure that “operations are conducted so as, Pinchot, 1st Chief of the Forest Service. where feasible, to minimize adverse environmental impacts on National Forest surface resources. 1 Table of Contents Project Context STIBNITE GOLD Project Location 4 Mining History at Stibnite 5 PROJECT Who is Midas Gold 6 Stibnite Plan of Operations PAYETTE & BOISE NATIONAL Proposed Mining Plan of FOREST - INTERMOUNTAIN REGION Operations 7 Open Pit Mining 8 Anadromous Fish - Tunnel 9 Inventoried Roadless Areas - Why is this project of interest to many Access and Powerline 10 people and organizations? Facilities During Mining Operations 10 5 million recoverable ounces of gold x -

Cinnabar and Mercury
CINNABAR AND MERCURY Specimens of bright-red cinnabar [mercury sulfide, HgS] have always attracted attention because of their color. While cinnabar (the name is of uncertain origin) usually occurs in granular or earthy forms, it sometimes forms distinctive, needle-like or tabular crystals with a quartz-like symmetry that are popular among mineral collectors. Cinnabar also has an unusual chemistry as one of the few mercury-containing minerals. Other collectible mercury minerals, all much less common than cinnabar, are livingstonite [mercury antimony sulfide, HgSb4S8], corderoite [mercury chlorosulfide, Hg3S2Cl2], coloradoite [mercury telluride, HgTe], and terlinguaite [mercury chlorate, Hg2ClO]. Cinnabar crystallizes in the trigonal (hexagonal) system, has a Mohs hardness of 2.0-2.5, and perfect cleavage in three directions. Among its unusual physical properties is a very high specific gravity of 8.0-8.2 that makes it the densest of all sulfide minerals. Because of its high density, cinnabar also has the highest index of refraction of any mineral—50 percent higher than that of diamond. From the standpoint of collecting, the most desirable and interesting cinnabar specimens are those with tiny, silvery droplets of elemental mercury. Mercury is named after the Roman god Mercurius; its chemical symbol, Hg, is from the Latin hydrargyrum, meaning “liquid silver.” Mercury forms on cinnabar specimens through an oxidation process in which oxygen combines with sulfur to produce sulfur dioxide and thus reduce the mercury to its elemental state. This reaction is easily demonstrated by placing a small piece of cinnabar in the oxidizing portion of a flame. Ranking 67th among the elements in crustal abundance, mercury is somewhat rare and only about as common as platinum. -

40 Common Minerals and Their Uses
40 Common Minerals and Their Uses Aluminum Beryllium The most abundant metal element in Earth’s Used in the nuclear industry and to crust. Aluminum originates as an oxide called make light, very strong alloys used in the alumina. Bauxite ore is the main source aircraft industry. Beryllium salts are used of aluminum and must be imported from in fluorescent lamps, in X-ray tubes and as Jamaica, Guinea, Brazil, Guyana, etc. Used a deoxidizer in bronze metallurgy. Beryl is in transportation (automobiles), packaging, the gem stones emerald and aquamarine. It building/construction, electrical, machinery is used in computers, telecommunication and other uses. The U.S. was 100 percent products, aerospace and defense import reliant for its aluminum in 2012. applications, appliances and automotive and consumer electronics. Also used in medical Antimony equipment. The U.S. was 10 percent import A native element; antimony metal is reliant in 2012. extracted from stibnite ore and other minerals. Used as a hardening alloy for Chromite lead, especially storage batteries and cable The U.S. consumes about 6 percent of world sheaths; also used in bearing metal, type chromite ore production in various forms metal, solder, collapsible tubes and foil, sheet of imported materials, such as chromite ore, and pipes and semiconductor technology. chromite chemicals, chromium ferroalloys, Antimony is used as a flame retardant, in chromium metal and stainless steel. Used fireworks, and in antimony salts are used in as an alloy and in stainless and heat resisting the rubber, chemical and textile industries, steel products. Used in chemical and as well as medicine and glassmaking. -

New Mineral Names*
AmericanMineralogM, Volume66, pages 1099-l103,IgEI NEW MINERAL NAMES* LouIs J. Cetnt, MrcHeer FtnrscHnn AND ADoLF Pnssr Aldermanlter Choloallte. I. R. Harrowficl4 E. R. Segnitand J. A. Watts (1981)Alderman- S. A. Williams (1981)Choloalite, CuPb(TeO3)z .HrO, a ncw min- ite, a ncw magnesiumalrrminum phosphate.Mineral. Mag.44, eral. Miaeral. Mag. 44, 55-51. 59-62. Choloalite was probably first found in Arabia, then at the Mina Aldermanite o@urs as minute, very thin" talc-likc crystallitcs La Oriental, Moctczuma, Sonora (the typc locality), and finally at with iuellite and other secondaryphosphates in the Moculta rock Tombstone, Arizona. Only thc Tombstone material provides para- phosphatc deposit near thc basc of Lower Cambrisn limestone genetic information. In this material choloalite occurs with cerus- close to Angaston, ca. 60 km NE of Adelaide. Microprobc analy- site, emmonsite and rodalquilarite in severcly brecciated shale that si.q supplcmented by gravimetric water determination gave MgO has been replaced by opal and granular jarosite. Wet chcmical E.4,CaO 1.2, AJ2O328.4, P2O5 25.9, H2O 36.1%,(totat 100),lead- analysisofcholoalitc from the type locality gave CuO 11.0,PbO ing to the formula Mg5Als2(POa)s(OH)zz.zH2O,where n = 32. 33.0,TeO2 50.7, H2O 3.4,total 98.1%,correspolding closcly to thc Thc powder diffraction pattern, taken with a Guinier camera, can formula in the titlc. Powder pattems of thc mineral from thc three be indexed on an orthorhombic. ccll with a = 15.000(7), D = localities can bc indexcd on the basis of a cubic ccll with a : 8.330(6),c - 26.60(l)A, Z = 2,D alc.2.15 from assumedcell con- l2.5l9A for the material from Mina La Oriental, Z: l2,D c,alc. -

Quicksilver-Antimony Deposits of Huitzuco, Guerrero, Mexico
UNITED STATES DEPARTMENT OF THE INXERIOR Harold L. Ickes, Secretary GEOLOGICAL SURVEY W. E. Wrather, Director Bulletin 946-B QUICKSILVER-ANTIMONY DEPOSITS OF HUITZUCO, GUERRERO, MEXICO BY JAMES F. McALLISTER ANJ? DAVID HERNANDEZ ORTIZ Prepared in cooperation with the UNIVERSIDAD NACIONAL DE MEXICO. INSTITUTO DE GEOLOGIA 'and SECRETARIA DE LA ECONOMIA NACIONAL DIRECCION GENERAL DE MINAS Y PETROLEO under the auspices of the INTERDEPARTMENTAL OOMMITTEE ON CULTURAL AND SCIENTIFIC COOPERATION, DEPARTMENT OF STATE Geolotic Investigations in the American Repul!lics, 1944 (Pages 49-71) UNITED STATES GOVERNMENT PRINTING OFFICE WASHINGTON : 1845 For sale by the Superintendent of Documents, U. S. Government Printing Oftice, Wasblnlton 25,. D. C. · Price 75 cents I I CONTENTS Page Abstract ••••••••••••••••••••••••••••••••••• • • • • • • • • • • • • • • • • 49 Introduction............................................... 49 History and production..................................... 52 Geology. • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • 53 Rock units •••••••••••••••••••••••••••·• • • • • • • • • • • • • • • • • • 55 Lim.estone •••••••• ••• ~............................... 55 Terrace gravel..................................... -55 Igneous rocks ••••••••••••••••••••••••• ·•••••••••• ; • • 58 Rocks formed by replacement........................ 58 Structure.............................................. 59 F'olds •..••_. • . • • • • . • • . • • . • . • . • . • . • • • • • . • • 60 Faults and other -

The Metallurgy of Antimony
Chemie der Erde 72 (2012) S4, 3–8 Contents lists available at SciVerse ScienceDirect Chemie der Erde journal homepage: www.elsevier.de/chemer The metallurgy of antimony Corby G. Anderson ∗ Kroll Institute for Extractive Metallurgy, George S. Ansell Department of Metallurgical and Materials Engineering, Colorado School of Mines, Golden, CO 80401, United States article info abstract Article history: Globally, the primary production of antimony is now isolated to a few countries and is dominated by Received 4 October 2011 China. As such it is currently deemed a critical and strategic material for modern society. The metallurgical Accepted 10 April 2012 principles utilized in antimony production are wide ranging. This paper will outline the mineral pro- cessing, pyrometallurgical, hydrometallurgical and electrometallurgical concepts used in the industrial Keywords: primary production of antimony. As well an overview of the occurrence, reserves, end uses, production, Antimony and quality will be provided. Stibnite © 2012 Elsevier GmbH. All rights reserved. Tetrahedrite Pyrometallurgy Hydrometallurgy Electrometallurgy Mineral processing Extractive metallurgy Production 1. Background bullets and armory. The start of mass production of automobiles gave a further boost to antimony, as it is a major constituent of Antimony is a silvery, white, brittle, crystalline solid that lead-acid batteries. The major use for antimony is now as a trioxide exhibits poor conductivity of electricity and heat. It has an atomic for flame-retardants. number of 51, an atomic weight of 122 and a density of 6.697 kg/m3 ◦ ◦ at 26 C. Antimony metal, also known as ‘regulus’, melts at 630 C 2. Occurrence and mineralogy and boils at 1380 ◦C. -
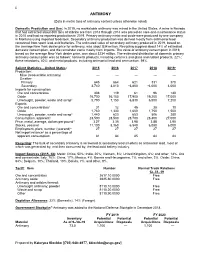
Antimony Data Sheet
22 ANTIMONY (Data in metric tons of antimony content unless otherwise noted) Domestic Production and Use: In 2019, no marketable antimony was mined in the United States. A mine in Nevada that had extracted about 800 tons of stibnite ore from 2013 through 2014 was placed on care-and-maintenance status in 2015 and had no reported production in 2019. Primary antimony metal and oxide were produced by one company in Montana using imported feedstock. Secondary antimony production was derived mostly from antimonial lead recovered from spent lead-acid batteries. The estimated value of secondary antimony produced in 2019, based on the average New York dealer price for antimony, was about $34 million. Recycling supplied about 14% of estimated domestic consumption, and the remainder came mostly from imports. The value of antimony consumption in 2019, based on the average New York dealer price, was about $234 million. The estimated distribution of domestic primary antimony consumption was as follows: nonmetal products, including ceramics and glass and rubber products, 22%; flame retardants, 40%; and metal products, including antimonial lead and ammunition, 39%. Salient Statistics—United States: 2015 2016 2017 2018 2019e Production: Mine (recoverable antimony) — — — — — Smelter: Primary 645 664 621 331 370 Secondary 3,740 3,810 e3,800 e4,000 4,000 Imports for consumption: Ore and concentrates 308 119 61 96 140 Oxide 16,700 16,100 17,900 19,200 17,000 Unwrought, powder, waste and scrap1 5,790 7,150 6,830 6,500 7,200 Exports: Ore and concentrates1 31 -

C:\Documents and Settings\Alan Smithee\My Documents\MOTM
Itmd1//8Lhmdq`knesgdLnmsg9Rshamhsd This month’s mineral is among the most collectible of all minerals. Ours come from a Chinese antimony mine that is now recognized as a classic stibnite locality, and our write-up explains the unusual structure and properties of stibnite, describes its remarkable crystals, and details the many uses of antimony. OVERVIEW PHYSICAL PROPERTIES Chemistry: Sb2S3 Antimony Trisulfide, often containing some bismuth Class: Sulfides Group: Stibnite Crystal System: Orthorhombic Crystal Habits: Individual bladed or acicular prisms or jumbled aggregates of prisms, striated lengthwise; prisms often bent or twisted; also as radiated groups and granular and massive forms. Color: Lead-gray and gray-black to steel-gray and silvery-gray, sometimes with a bluish hue; occasionally iridescent; tarnish black. Luster: Metallic Transparency: Opaque Streak: Dark lead-gray Refractive Index: None (opaque) Cleavage: Perfect in one direction lengthwise Figure 1. Stibnite crytals. Fracture: Subconchoidal to irregular; brittle; thin prisms are slightly flexible. Hardness: 2.0 Specific Gravity: 4.6 Luminescence: None Distinctive Features and Tests: Best field identification features are softness; flexibility of thin prisms; and long, bladed and acicular crystal habits. Visually similar to bismuthinite [bismuth trisulfide, Bi2S3], which has considerably more density. Dana Classification Number: 2.11.2.1 NAME Stibnite, pronounced STIBB-nite, derives from stibi, the Greek name for the mineral. Stibnite has formerly been referred to as “antimonite,” “antimonide,” “sulfur antimonide,” “sulfur antimony,” “antimony glance,” “gray antimony,” “gray antimony ore,” “kohl,” “stibi,” “stimmi,” “stibium,” “lupus metallorum,” “platyophthalmite,” and “speissglas.” In current European mineralogical literature, stibnite appears as stibnit, stibnita, and stibnine. Antimony, pronounced ANN-tih-mow-nee, stems from the Latin word for the metal, antimonium, which means “opposed to solitude,” in allusion to its rare occurrence as a native element. -

Minerals of Bismuthinite-Stibnite Series with Special Reference to Horobetsuite from the Horobetsu Mine, Hokkaido, Japan*
MINERALOGICAL JOURNAL VOL . 1, No. 4, pp. 189-197, JUNE, 1955 MINERALS OF BISMUTHINITE-STIBNITE SERIES WITH SPECIAL REFERENCE TO HOROBETSUITE FROM THE HOROBETSU MINE, HOKKAIDO, JAPAN* KITARO HAYASE Institute of Mining, Faculty of Science and Engineering , Waseda University. ABSTRACT Horobetsuite occurs associated with free sulphur and iron sulphide minerals, in the sulphur deposit of Horobetsu Mine. The chemical formula of horobetsuite has been determined as (Bi, Sb)2S3. The molecular ratio of Bi2S3 to Sb2S3 varies between 9:11 and 13:7. The mineral is intermediate between bismuthinite and stibnite in lattice constant, specific gravity, optical behaviour and etching reac tion. The data obtained reveal the mineral to be a new species belonging to the bismuthinite-stibnite series. A new mineral name, horobetsuite, is proposed for the mineral of the series which should have the molecular ratio of Bi2S3 to Sb2S3 between 7:3 and 3:7. Introduction The writer1) once reported the results of the study of a Bi-Sb sul phide mineral that occurred at the Horobetsu mine, and suggested that it might represent a solid solution of bismuthinite and stibnite. The slight fluctuation observed of the molecular ratio of Bi2S3 to Sb2S3 has prompt us to a further study. Occurrence of horobetsuitel) The Horobetsu mine in which horobetsuite occurs is located at Sobetsu Village, Usu County, in the vicinity of Muroran, Hokkaido, Japan. (Fig. 1) * Read at the Annual Meeting of the Mineralogical Society of Japan held in Tokyo on June 4, 1954. 190 Minerals of Bismuthinite-Stibnite Series Fig. 1. Sulphur ore body of Horobetsu Mine. -

Antimony Deposits of Alaska
DEPARTMENT OF THE INTERIOR FRANKLIN K. LANE, Secretary UNITED STATES GEOLOGICAL SURVEY GEORGE OTIS SMITH, Director Bulletin 649 ANTIMONY DEPOSITS OF ALASKA BY ALFRED H. BROOKS WASHINGTON GOVERNMENT PRINTING OFFICE 1916 CONTENTS. Page. Introduction.............................................................. 5 Mining developments and production........................................ 6 Geographic distribution....................:............................... 8 Geology.................................................................. .9 Occurrence of the antimony deposits................................... 9 Country rock......................................................... 9 Ore bodies............................................................ 10 Classification.................................-.----.-------------- 10 Siliceous gold-bearing stibnite lodes................................ 10 Stibnite-cinnabar lodes. ............................................ 12 Stibnite-galena deposits........................................... 12 Influence of coxmtry rock........................................... 13 Vertical distribution of ores........................................ 13 Oxidation......................................................... 13 Age of mineralization............................................... 14 Localities.................................................. 1............... 17 Fairbanks district. ..................................................... 17 Development of antimony deposits................................. -

A Specific Gravity Index for Minerats
A SPECIFICGRAVITY INDEX FOR MINERATS c. A. MURSKyI ern R. M. THOMPSON, Un'fuersityof Bri.ti,sh Col,umb,in,Voncouver, Canad,a This work was undertaken in order to provide a practical, and as far as possible,a complete list of specific gravities of minerals. An accurate speciflc cravity determination can usually be made quickly and this information when combined with other physical properties commonly leads to rapid mineral identification. Early complete but now outdated specific gravity lists are those of Miers given in his mineralogy textbook (1902),and Spencer(M,i,n. Mag.,2!, pp. 382-865,I}ZZ). A more recent list by Hurlbut (Dana's Manuatr of M,i,neral,ogy,LgE2) is incomplete and others are limited to rock forming minerals,Trdger (Tabel,l,enntr-optischen Best'i,mmungd,er geste,i,nsb.ildend,en M,ineral,e, 1952) and Morey (Encycto- ped,iaof Cherni,cal,Technol,ogy, Vol. 12, 19b4). In his mineral identification tables, smith (rd,entifi,cati,onand. qual,itatioe cherai,cal,anal,ys'i,s of mineral,s,second edition, New york, 19bB) groups minerals on the basis of specificgravity but in each of the twelve groups the minerals are listed in order of decreasinghardness. The present work should not be regarded as an index of all known minerals as the specificgravities of many minerals are unknown or known only approximately and are omitted from the current list. The list, in order of increasing specific gravity, includes all minerals without regard to other physical properties or to chemical composition. The designation I or II after the name indicates that the mineral falls in the classesof minerals describedin Dana Systemof M'ineralogyEdition 7, volume I (Native elements, sulphides, oxides, etc.) or II (Halides, carbonates, etc.) (L944 and 1951). -

STIBNITE GOLD PROJECT Valley County, Idaho
STIBNITE GOLD PROJECT Valley County, Idaho REFINED PROPOSED ACTION MODPRO2 Midas Gold Idaho, Inc. PO Box 429 13181 Hwy 55 December 2020 Donnelly, ID 83615 STIBNITE GOLD PROJECT REFINED PROPOSED ACTION – MODPRO2 Summary This document describes Midas Gold Idaho, Inc.’s (Midas Gold’s) proposed further refinements of the Stibnite Gold Project (SGP) Plan of Restoration and Operations (PRO) (Midas Gold, 2016) and presents Midas Gold’s updated proposed action, the ModPRO21. The ModPRO2 was developed to further reduce potential environmental impacts of the SGP in alignment with Midas Gold’s Core Values as set out in the PRO (Section 2), Conservation Principles (PRO Section 2), its Sustainability Goals (PRO Section 2.4) and its Environmental Goals (PRO Section 6.2). Project refinements included in the ModPRO2: (1) are supported by udpated data and analysis that identify opportunities to reduce potential environmental impacts; (2) address persistent potential environmental impacts not sufficiently ameliorated or reduced by project refinements included in the original ModPRO; (3) are informed by public and reviewing agencies’ comments on the DEIS, and; (4) align with the National Environmental Policy Act (NEPA) and all applicable Federal, State and Local regulations and permit requirements. The ModPRO2 also aligns with the project development approach in Midas Gold’s Feasibility Study (FS) (M3, 2020). The ModPRO2 is presented in three sections and an appendix: • Section 1 describes the evolution of the ModPRO2 in the context of the original proposed action (the PRO) and alternatives evaluated in the SGP Draft Environmental Impact Statement (DEIS) including the ModPRO (DEIS Alternative 2). • Section 2 provides the justification and approach for refinements to components of the SGP that result in the ModPRO2.