DOCSLIB.ORG

ABSTRACTS Mailing Offi MATHEMATICS and Additional of Papers Presented to the Periodicals Postage 2010

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

A ces BSTRACTS ABSTRACTS mailing offi MATHEMATICS and additional of Papers Presented to the Periodicals postage 2010 paid at Providence, RI American Mathematical Society SUBJECT CLASSIFICATION Volume 33, Number 2, Issue 168 Spring 2012 Compiled in the Editorial Offices of MATHEMATICAL REVIEWS and ZENTRALBLATT MATH 00 General 44 Integral transforms, operational calculus 01 History and biography 45 Integral equations Editorial Committee 03 Mathematical logic and foundations 46 Functional analysis 05 Combinatorics 47 Operator theory Robert J. Daverman, Chair Volume 33 • Number 2 Spring 2012 Volume 06 Order, lattices, ordered 49 Calculus of variations and optimal Georgia Benkart algebraic structures control; optimization 08 General algebraic systems 51 Geometry Michel L. Lapidus 11 Number theory 52 Convex and discrete geometry Matthew Miller 12 Field theory and polynomials 53 Differential geometry 13 Commutative rings and algebras 54 General topology Steven H. Weintraub 14 Algebraic geometry 55 Algebraic topology 15 Linear and multilinear algebra; 57 Manifolds and cell complexes matrix theory 58 Global analysis, analysis on manifolds 16 Associative rings and algebras 60 Probability theory and stochastic 17 Nonassociative rings and algebras processes Abstracts for 18 Category theory; homological 62 Statistics algebra 65 Numerical analysis Honolulu, March 3–4, 2012 ........................ 537 19 K-theory 68 Computer science 20 Group theory and generalizations 70 Mechanics of particles and systems Tampa, March 10–11, 2012 ........................ 611 22 Topological groups, Lie groups 74 Mechanics of deformable solids 26 Real functions 76 Fluid mechanics 28 Measure and integration 78 Optics, electromagnetic theory Washington, March 17–18, 2012 ................. 691 30 Functions of a complex variable 80 Classical thermodynamics, heat transfer 31 Potential theory 81 Quantum theory Lawrence, March 30–April 1, 2012 ..............757 32 Several complex variables and 82 Statistical mechanics, structure of matter analytic spaces 83 Relativity and gravitational theory 33 Special functions 85 Astronomy and astrophysics 34 Ordinary differential equations 86 Geophysics 35 Partial differential equations 90 Operations research, mathematical 37 Dynamical systems and ergodic programming theory 91 Game theory, economics, social and 39 Difference and functional equations behavioral sciences 40 Sequences, series, summability 92 Biology and other natural sciences 41 Approximations and expansions 93 Systems theory; control 42 Fourier analysis 94 Information and communication, circuits 43 Abstract harmonic analysis 97 Mathematics education ISSN 0192-5857 Pages 537–826 AMS Abstracts of Papers Presented to the AMS Abstracts of Papers Presented ISSN 0192-5857 American Mathematical Society 201 Charles Street, Providence, RI 02904-2294 USA GST No. R121892046 AMS License or copyright restrictions may apply to redistribution; see https://www.ams.org/journal-terms-of-use 296 Pages on 40 lb paper • Spine: 7/16" • Print in Black Ink • Trim 7" x 10" SUBMISSION INFORMATION ABSTRACTS PUBLISHED IN THIS JOURNAL are those submitted by authors who intend to present them at AMS meetings (see the front cover). The abstracts for each meeting are sorted by the two-digit 2010 Mathematics Subject Classification chosen by the author and appear in the order received. See the back cover for the 2010 Mathematics Subject Classification. THE SUITABILITY OF A PAPER for presentation to the Society is judged from the abstract as outlined in Article X, Section 6 of the bylaws: Papers intended for presentation at any meeting of the Society shall be passed upon in advance by a program committee appointed by or under the authority of the Council; and only such papers shall be presented as shall have been approved by such committee. Papers in a form unsuitable for publication, if accepted for presentation, shall be referred to on the program as preliminary communications or reports. In addition, the editors of the Abstracts have adopted the following policy: In order to be accepted for publication, an abstract must have mathematical research content. It should not contain libelous, defamatory, or tasteless remarks, commercial promotions, nor political or religious arguments. Papers may not be presented if published in full before the date of the Society meeting or if previously presented to any learned Society except the National Academy of Sciences or the Royal Society of Canada. The AMS assumes no responsibility for the content or inappropriate remarks in any published abstract. GENERAL INFORMATION ON ABSTRACTS is found at http://www.ams.org/abstracts. ABSTRACTS ARE PRINTED from copy submitted by the author. Web submission is the required electronic format. To access the interactive template, visit the Abstracts submission page on the AMS website at http://www.ams.org/ cgi-bin/abstracts/abstract.pl. Step-by-step submission instructions are included in the template. No knowl- edge of LATEX is necessary; however, any mathematical displays or accent marks in text or in names must be coded in LATEX. Requests for general information concerning abstracts may be sent to [email protected]. THE ABSTRACT RECEIPT DEADLINES FOR ALL MEETINGS will be strictly enforced. Unfortunately, late papers cannot be accommodated. When all talks have been scheduled for a given meeting, the attendant abstracts will be available for viewing on the AMS website through the program display for that meeting. NOTATIONS IN THIS JOURNAL are the following: * Indicates who will present the paper at the meeting. SUBSCRIPTION INFORMATION CHANGES OF ADDRESS should be reported six weeks in advance to avoid disruption of service. Changes of address and all general correspondence should be sent to Member and Customer Services, American Mathematical Society, 201 Charles Street, Providence, RI 02904-2294 USA (email: [email protected] or fax: 401-455-4026); dues payments and orders for AMS publications should be addressed to the Society at P.O. Box 845904, Boston, MA 02284-5904 USA; all correspondence relating to advance registration for meetings should be addressed to the Society, 201 Charles Street, Providence, RI 02904-2294 USA. Abstracts of Papers Presented to the American Mathematical Society (ISSN 0192-5857) is published four times a year by the American Mathematical Society at 201 Charles Street, Providence, RI 02904-2294. The subscription price for Volume 33 (2012) is US$156 list, US$124.80 institutional member, US$93.60 individual member. Subscription renewals are subject to late fees. See www.ams.org/customers/macs-faq.html#journal for more information. Periodicals postage paid at Providence, RI. Add for postage: Surface delivery to destinations outside the U.S.—US$11, to India—US$18. Expedited delivery to destinations in North America—US$14, elsewhere—US$41. POSTMASTER: Send address change notices to Abstracts of Papers Presented to the American Mathematical Society, 201 Charles Street, Providence, RI 02904-2294 USA. c 2012 by the American Mathematical Society. All rights reserved. Printed in the United States of America. ∞ This journal is printed on acid-free paper and falls within the guidelines established to ensure permanence and durability. License or copyright restrictions may apply to redistribution; see https://www.ams.org/journal-terms-of-use 10 9 8 7 6 5 4 3 2 1 16 15 14 13 12 PAPERS PRESENTED AT MEETINGS THIS CALENDAR lists meetings of the Society which have been approved by the Council at which papers may be presented. Programs of Annual Meetings appear in the Notices andontheAMSwebsite;programs for sectional meetings appear on the AMS Web pages in the Meetings & Conferences section, and are electronically archived in the Notices section on the AMS website. ABSTRACT ABSTRACT MEETING # DATE PLACE DEADLINE ISSUE 1082 September 22–23, 2012 Rochester, NY July 10 Vol 33, No. 3 1083 October 13–14, 2012 New Orleans, LA August 28 Vol 33, No. 3 1084 October 20–21, 2012 Akron, OH September 4 Vol 33, No. 4 1085 October 27–28, 2012 Tucson, AZ September 11 Vol 33, No. 4 1086 January 9–12, 2013 San Diego, CA TBA Vol 34, No. 1 1087 March 1–3, 2013 Oxford, MS TBA TBA 1088 April 6–7, 2013 Chestnut Hill, MA TBA TBA 1089 April 13–14, 2013 Boulder, CO February 19 TBA 1090 April 27–28, 2013 Ames, IA TBA TBA 1091 June 27–30, 2013 Alba Iulia, Romania TBA NA 1092 October 5–6, 2013 Louisville, KY TBA TBA 1093 October 12–13, 2013 Philadelphia, PA TBA TBA 1094 October 18–20, 2013 St. Louis, MO TBA TBA 1095 November 2–3, 2013 Riverside, CA September 10 TBA HONOLULU, HI, March 3–4, 2012 Abstracts of the 1078th Meeting. 03 Mathematical logic and foundations 1078-03-34 John Goodrick, Department of Mathematics, Universidad de los Andes, Bogota, Colombia, Byunghan Kim*, Department of Mathematics, Yonsei University, Seoul, South Korea, and Alexei Kolesnikov, Department of Mathematics, Towson University, Towson, MD. Amalgamation functors and homology groups in model theory, part I. In this joint work of John Goodrick, Byunghan Kim, and Alexei Kolesnikov, we develop basics of homology theory in a model-theoretic context and connect it with generalized amalgamation properties. This talk will introduce definitions of homology groups Hn, n ≥ 0, associated to a family of “amalgamation functors”. Main resutls are: If the generalized amalgamation properties hold, then the homology groups are trivial; H2 for strong types in stable theories are profinite abelian. (Received November 03, 2011) 1078-03-35 John Goodrick, Byunghan Kim and Alexei Kolesnikov* ([email protected]), Department of Mathematics, Towson University, 8000 York Rd., Towson, MD 21252. Amalgamation functors and homology groups in model theory, part II. This talk will continue the exposition of the work by John Goodrick, Byunghan Kim, and Alexei Kolesnikov. We will present examples illustrating the main notions, outline the proof of the “Prism Lemma” (an important technical result used in the calculation of the homology groups). Finally, we will compute the group H2 for strong types in stable theories and show that any profinite abelian group can occur as the group H2 in the model-theoretic context.
Recommended publications
  • Extreme and Exposed Representing Measures of the Disk Algebra

    Extreme and Exposed Representing Measures of the Disk Algebra

    ANNALES POLONICI MATHEMATICI LXXIII.2 (2000) Extreme and exposed representing measures of the disk algebra by Alex Heinis (Leiden) and Jan Wiegerinck (Amsterdam) Abstract. We study the extreme and exposed points of the convex set consisting of representing measures of the disk algebra, supported in the closed unit disk. A boundary point of this set is shown to be extreme (and even exposed) if its support inside the open unit disk consists of two points that do not lie on the same radius of the disk. If its support inside the unit disk consists of 3 or more points, it is very seldom an extreme point. We also give a necessary condition for extreme points to be exposed and show that so-called BSZ-measures are never exposed. 1. Introduction and notational matters. In a previous paper [2] Brummelhuis and the second author studied representing measures for the disk algebra A = A(D)= {f ∈ C(D) | f is holomorphic on D}, where D is the unit disk in C. As usual A is endowed with the structure of a uniform algebra. Its spectrum equals D. That is, every homomorphism φ : A → C is of the form f 7→ f(x) for some x ∈ D. The Hahn–Banach theorem allows for a multitude of extensions of φ as a continuous linear functional on C(D). The dual space C(D)∗ can be identified with M, the space of complex Borel measures on D endowed with the weak∗ topology by the Riesz representation theorem. A representing measure µ for x ∈ D is a positive Borel measure on D such that \ f dµ = f(x) ∀f ∈ A.
  • Volcanic History of the Imbrium Basin: a Close-Up View from the Lunar Rover Yutu

    Volcanic History of the Imbrium Basin: a Close-Up View from the Lunar Rover Yutu

    Volcanic history of the Imbrium basin: A close-up view from the lunar rover Yutu Jinhai Zhanga, Wei Yanga, Sen Hua, Yangting Lina,1, Guangyou Fangb, Chunlai Lic, Wenxi Pengd, Sanyuan Zhue, Zhiping Hef, Bin Zhoub, Hongyu Ling, Jianfeng Yangh, Enhai Liui, Yuchen Xua, Jianyu Wangf, Zhenxing Yaoa, Yongliao Zouc, Jun Yanc, and Ziyuan Ouyangj aKey Laboratory of Earth and Planetary Physics, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China; bInstitute of Electronics, Chinese Academy of Sciences, Beijing 100190, China; cNational Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China; dInstitute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China; eKey Laboratory of Mineralogy and Metallogeny, Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, Guangzhou 510640, China; fKey Laboratory of Space Active Opto-Electronics Technology, Shanghai Institute of Technical Physics, Chinese Academy of Sciences, Shanghai 200083, China; gThe Fifth Laboratory, Beijing Institute of Space Mechanics & Electricity, Beijing 100076, China; hXi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi’an 710119, China; iInstitute of Optics and Electronics, Chinese Academy of Sciences, Chengdu 610209, China; and jInstitute of Geochemistry, Chinese Academy of Science, Guiyang 550002, China Edited by Mark H. Thiemens, University of California, San Diego, La Jolla, CA, and approved March 24, 2015 (received for review February 13, 2015) We report the surface exploration by the lunar rover Yutu that flows in Mare Imbrium was obtained only by remote sensing from landed on the young lava flow in the northeastern part of the orbit. On December 14, 2013, Chang’e-3 successfully landed on the Mare Imbrium, which is the largest basin on the nearside of the young and high-Ti lava flow in the northeastern Mare Imbrium, Moon and is filled with several basalt units estimated to date from about 10 km south from the old low-Ti basalt unit (Fig.
  • Of Vertebrate Fossils from the Middle Eocene Oil Shale of Messel, Germany: Implications for Their Taphonomy and Palaeoenvironment

    Of Vertebrate Fossils from the Middle Eocene Oil Shale of Messel, Germany: Implications for Their Taphonomy and Palaeoenvironment

    Palaeogeography, Palaeoclimatology, Palaeoecology 416 (2014) 92–109 Contents lists available at ScienceDirect Palaeogeography, Palaeoclimatology, Palaeoecology journal homepage: www.elsevier.com/locate/palaeo Isotope compositions (C, O, Sr, Nd) of vertebrate fossils from the Middle Eocene oil shale of Messel, Germany: Implications for their taphonomy and palaeoenvironment Thomas Tütken ⁎ Steinmann-Institut für Geologie, Mineralogie und Paläontologie, Universität Bonn, Poppelsdorfer Schloss, 53115 Bonn, Germany article info abstract Article history: The Middle Eocene oil shale deposits of Messel are famous for their exceptionally well-preserved, articulated 47- Received 15 April 2014 Myr-old vertebrate fossils that often still display soft tissue preservation. The isotopic compositions (O, C, Sr, Nd) Received in revised form 30 July 2014 were analysed from skeletal remains of Messel's terrestrial and aquatic vertebrates to determine the condition of Accepted 5 August 2014 geochemical preservation. Authigenic phosphate minerals and siderite were also analysed to characterise the iso- Available online 17 August 2014 tope compositions of diagenetic phases. In Messel, diagenetic end member values of the volcanically-influenced 12 Keywords: and (due to methanogenesis) C-depleted anoxic bottom water of the meromictic Eocene maar lake are isoto- Strontium isotopes pically very distinct from in vivo bioapatite values of terrestrial vertebrates. This unique taphonomic setting al- Oxygen isotopes lows the assessment of the geochemical preservation of the vertebrate fossils. A combined multi-isotope Diagenesis approach demonstrates that enamel of fossil vertebrates from Messel is geochemically exceptionally well- Enamel preserved and still contains near-in vivo C, O, Sr and possibly even Nd isotope compositions while bone and den- Messel tine are diagenetically altered.
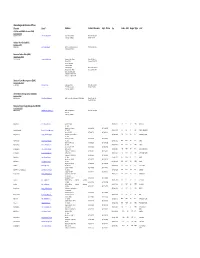
  • Alaska Regional Directors Offices Director Email Address Contact Numbers Supt

    Alaska Regional Directors Offices Director Email Address Contact Numbers Supt

    Alaska Regional Directors Offices Director Email Address Contact Numbers Supt. Phone Fax Code ABLI RegionType Unit U.S Fish and Wildlife Service (FWS) Alaska Region (FWS) HASKETT,GEOFFREY [email protected] 1011 East Tudor Road Phone: 907‐ 786‐3309 Anchorage, AK 99503 Fax: 907‐ 786‐3495 Naitonal Park Service(NPS) Alaska Region (NPS) MASICA,SUE [email protected] 240 West 5th Avenue,Suite 114 Phone:907‐644‐3510 Anchoorage,AK 99501 Bureau of Indian Affairs(BIA) Alaska Region (BIA) VIRDEN,EUGENE [email protected] Bureau of Indian Affairs Phone: 907‐586‐7177 PO Box 25520 Telefax: 907‐586‐7252 709 West 9th Street Juneau, AK 99802 Anchorage Agency Phone: 1‐800‐645‐8465 Bureau of Indian Affairs Telefax:907 271‐4477 3601 C Street Suite 1100 Anchorage, AK 99503‐5947 Telephone: 1‐800‐645‐8465 Bureau of Land Manangement (BLM) Alaska State Office (BLM) CRIBLEY,BUD [email protected] Alaska State Office Phone: 907‐271‐5960 222 W 7th Avenue #13 FAX: 907‐271‐3684 Anchorage, AK 99513 United States Geological Survey(USGS) Alaska Area (USGS) BARTELS,LESLIE lholland‐[email protected] 4210 University Dr., Anchorage, AK 99508‐4626 Phone:907‐786‐7055 Fax: 907‐ 786‐7040 Bureau of Ocean Energy Management(BOEM) Alaska Region (BOEM) KENDALL,JAMES [email protected] 3801 Centerpoint Drive Phone: 907‐ 334‐5208 Suite 500 Anchorage, AK 99503 Ralph Moore [email protected] c/o Katmai NP&P (907) 246‐2116 ANIA ANTI AKR NPRES ANIAKCHAK P.O. Box 7 King Salmon, AK 99613 (907) 246‐3305 (907) 246‐2120 Jeanette Pomrenke [email protected] P.O.
  • The Jacobson Radical of Semicrossed Products of the Disk Algebra

    The Jacobson Radical of Semicrossed Products of the Disk Algebra

    Iowa State University Capstones, Theses and Graduate Theses and Dissertations Dissertations 2012 The aJ cobson radical of semicrossed products of the disk algebra Anchalee Khemphet Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/etd Part of the Mathematics Commons Recommended Citation Khemphet, Anchalee, "The aJ cobson radical of semicrossed products of the disk algebra" (2012). Graduate Theses and Dissertations. 12364. https://lib.dr.iastate.edu/etd/12364 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. The Jacobson radical of semicrossed products of the disk algebra by Anchalee Khemphet A dissertation submitted to the graduate faculty in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY Major: Mathematics Program of Study Committee: Justin Peters, Major Professor Scott Hansen Dan Nordman Paul Sacks Sung-Yell Song Iowa State University Ames, Iowa 2012 Copyright c Anchalee Khemphet, 2012. All rights reserved. ii DEDICATION I would like to dedicate this thesis to my father Pleng and to my mother Supavita without whose support I would not have been able to complete this work. I would also like to thank my friends and family for their loving guidance and to my government for financial assistance during the writing of this work. iii TABLE OF CONTENTS ACKNOWLEDGEMENTS . v ABSTRACT . vi CHAPTER 1.
  • Arxiv:0705.1142V1 [Math.DS] 8 May 2007 Cases New) and Are Ripe for Further Study

    Arxiv:0705.1142V1 [Math.DS] 8 May 2007 Cases New) and Are Ripe for Further Study

    A PRIMER ON SUBSTITUTION TILINGS OF THE EUCLIDEAN PLANE NATALIE PRIEBE FRANK Abstract. This paper is intended to provide an introduction to the theory of substitution tilings. For our purposes, tiling substitution rules are divided into two broad classes: geometric and combi- natorial. Geometric substitution tilings include self-similar tilings such as the well-known Penrose tilings; for this class there is a substantial body of research in the literature. Combinatorial sub- stitutions are just beginning to be examined, and some of what we present here is new. We give numerous examples, mention selected major results, discuss connections between the two classes of substitutions, include current research perspectives and questions, and provide an extensive bib- liography. Although the author attempts to fairly represent the as a whole, the paper is not an exhaustive survey, and she apologizes for any important omissions. 1. Introduction d A tiling substitution rule is a rule that can be used to construct infinite tilings of R using a finite number of tile types. The rule tells us how to \substitute" each tile type by a finite configuration of tiles in a way that can be repeated, growing ever larger pieces of tiling at each stage. In the d limit, an infinite tiling of R is obtained. In this paper we take the perspective that there are two major classes of tiling substitution rules: those based on a linear expansion map and those relying instead upon a sort of \concatenation" of tiles. The first class, which we call geometric tiling substitutions, includes self-similar tilings, of which there are several well-known examples including the Penrose tilings.
  • Combinatorial Design University of Southern California Non-Parametric Computational Design Strategies

    Combinatorial Design University of Southern California Non-Parametric Computational Design Strategies

    Jose Sanchez Combinatorial design University of Southern California Non-parametric computational design strategies 1 ABSTRACT This paper outlines a framework and conceptualization of combinatorial design. Combinatorial 1 Design – Year 3 – Pattern of one design is a term coined to describe non-parametric design strategies that focus on the permutation, unit in two scales. Developed by combinatorial design within a game combination and patterning of discrete units. These design strategies differ substantially from para- engine. metric design strategies as they do not operate under continuous numerical evaluations, intervals or ratios but rather finite discrete sets. The conceptualization of this term and the differences with other design strategies are portrayed by the work done in the last 3 years of research at University of Southern California under the Polyomino agenda. The work, conducted together with students, has studied the use of discrete sets and combinatorial strategies within virtual reality environments to allow for an enhanced decision making process, one in which human intuition is coupled to algo- rithmic intelligence. The work of the research unit has been sponsored and tested by the company Stratays for ongoing research on crowd-sourced design. 44 INTRODUCTION—OUTSIDE THE PARAMETRIC UMBRELLA To start, it is important that we understand that the use of the terms parametric and combinatorial that will be used in this paper will come from an architectural and design background, as the association of these terms in mathematics and statistics might have a different connotation. There are certainly lessons and a direct relation between the term ‘combinatorial’ as used in this paper and the field of combinatorics and permutations in mathematics.
  • Discover Linear Algebra Incomplete Preliminary Draft

    Discover Linear Algebra Incomplete Preliminary Draft

    Discover Linear Algebra Incomplete Preliminary Draft Date: November 28, 2017 L´aszl´oBabai in collaboration with Noah Halford All rights reserved. Approved for instructional use only. Commercial distribution prohibited. c 2016 L´aszl´oBabai. Last updated: November 10, 2016 Preface TO BE WRITTEN. Babai: Discover Linear Algebra. ii This chapter last updated August 21, 2016 c 2016 L´aszl´oBabai. Contents Notation ix I Matrix Theory 1 Introduction to Part I 2 1 (F, R) Column Vectors 3 1.1 (F) Column vector basics . 3 1.1.1 The domain of scalars . 3 1.2 (F) Subspaces and span . 6 1.3 (F) Linear independence and the First Miracle of Linear Algebra . 8 1.4 (F) Dot product . 12 1.5 (R) Dot product over R ................................. 14 1.6 (F) Additional exercises . 14 2 (F) Matrices 15 2.1 Matrix basics . 15 2.2 Matrix multiplication . 18 2.3 Arithmetic of diagonal and triangular matrices . 22 2.4 Permutation Matrices . 24 2.5 Additional exercises . 26 3 (F) Matrix Rank 28 3.1 Column and row rank . 28 iii iv CONTENTS 3.2 Elementary operations and Gaussian elimination . 29 3.3 Invariance of column and row rank, the Second Miracle of Linear Algebra . 31 3.4 Matrix rank and invertibility . 33 3.5 Codimension (optional) . 34 3.6 Additional exercises . 35 4 (F) Theory of Systems of Linear Equations I: Qualitative Theory 38 4.1 Homogeneous systems of linear equations . 38 4.2 General systems of linear equations . 40 5 (F, R) Affine and Convex Combinations (optional) 42 5.1 (F) Affine combinations .
  • Actual Problems Актуальные Проблемы

    Actual Problems Актуальные Проблемы

    АКАДЕМИЯ НАУК АВИАЦИИ И ВОЗДУХОПЛАВАНИЯ РОССИЙСКАЯ АКАДЕМИЯ КОСМОНАВТИКИ ИМ. К.Э.ЦИОЛКОВСКОГО ACADEMY OF AVIATION AND AERONAUTICS SCIENCES RUSSIAN ASTRONAUTICS ACADEMY OF K.E.TSIOLKOVSKY'S NAME СССР 7 195 ISSN 1727-6853 12.04.1961 АКТУАЛЬНЫЕ ПРОБЛЕМЫ АВИАЦИОННЫХ И АЭРОКОСМИЧЕСКИХ СИСТЕМ процессы, модели, эксперимент 2(39) 2014 RUSSIAN-AMERICAN SCIENTIFIC JOURNAL ACTUAL PROBLEMS OF AVIATION AND AEROSPACE SYSTEMS processes, models, experiment УРНАЛ УЧНЫЙ Ж О-АМЕРИКАНСКИЙ НА ОССИЙСК Р Казань Daytona Beach А К Т УА Л Ь Н Ы Е П Р О Б Л Е М Ы А В И А Ц И О Н Н Ы Х И А Э Р О К О С М И Ч Е С К И Х С И С Т Е М Казань, Дайтона Бич Вып. 2 (39), том 19, 1-206, 2014 СОДЕРЖАНИЕ CONTENTS Г.В.Новожилов 1 G.V.Novozhilov К 120-летию авиаконструктора To the 120-th Anniversary of Сергея Владимировича Ильюшина Sergey Vladimirovich Ilyushin А.Болонкин 14 A.Bolonkin Использование энергии ветра Utilization of wind energy at high больших высот altitude Эмилио Спедикато 46 Emilio Spedicato О моделировании взаимодействия About modelling interaction of Earth Земли с крупным космическим with large space object: the script with объектом: сценарий взрыва Фаэтона explosion of Phaeton and the sub- и последующей эволюции sequent evolution of Mankind (part II) Человечества (часть II) М.В.Левский 76 M.V.Levskii Оптимальное по времени The time-optimal control of motion of a управление движением spacecraft with inertial executive космического аппарата с devices инерционными исполнительными органами В.А.Афанасьев, А.С.Мещанов, 99 V.A.Afanasyev, A.S.Meshchanov, Е.Ю.Самышева
  • The Book Review Column1 by William Gasarch Department of Computer Science University of Maryland at College Park College Park, MD, 20742 Email: Gasarch@Cs.Umd.Edu

    The Book Review Column1 by William Gasarch Department of Computer Science University of Maryland at College Park College Park, MD, 20742 Email: [email protected]

    The Book Review Column1 by William Gasarch Department of Computer Science University of Maryland at College Park College Park, MD, 20742 email: [email protected] In this column we review the following books. 1. Combinatorial Designs: Constructions and Analysis by Douglas R. Stinson. Review by Gregory Taylor. A combinatorial design is a set of sets of (say) {1, . , n} that have various properties, such as that no two of them have a large intersection. For what parameters do such designs exist? This is an interesting question that touches on many branches of math for both origin and application. 2. Combinatorics of Permutations by Mikl´osB´ona. Review by Gregory Taylor. Usually permutations are viewed as a tool in combinatorics. In this book they are considered as objects worthy of study in and of themselves. 3. Enumerative Combinatorics by Charalambos A. Charalambides. Review by Sergey Ki- taev, 2008. Enumerative combinatorics is a branch of combinatorics concerned with counting objects satisfying certain criteria. This is a far reaching and deep question. 4. Geometric Algebra for Computer Science by L. Dorst, D. Fontijne, and S. Mann. Review by B. Fasy and D. Millman. How can we view Geometry in terms that a computer can understand and deal with? This book helps answer that question. 5. Privacy on the Line: The Politics of Wiretapping and Encryption by Whitfield Diffie and Susan Landau. Review by Richard Jankowski. What is the status of your privacy given current technology and law? Read this book and find out! Books I want Reviewed If you want a FREE copy of one of these books in exchange for a review, then email me at gasarchcs.umd.edu Reviews need to be in LaTeX, LaTeX2e, or Plaintext.
  • The Language of Differential Forms

    The Language of Differential Forms

    Appendix A The Language of Differential Forms This appendix—with the only exception of Sect.A.4.2—does not contain any new physical notions with respect to the previous chapters, but has the purpose of deriving and rewriting some of the previous results using a different language: the language of the so-called differential (or exterior) forms. Thanks to this language we can rewrite all equations in a more compact form, where all tensor indices referred to the diffeomorphisms of the curved space–time are “hidden” inside the variables, with great formal simplifications and benefits (especially in the context of the variational computations). The matter of this appendix is not intended to provide a complete nor a rigorous introduction to this formalism: it should be regarded only as a first, intuitive and oper- ational approach to the calculus of differential forms (also called exterior calculus, or “Cartan calculus”). The main purpose is to quickly put the reader in the position of understanding, and also independently performing, various computations typical of a geometric model of gravity. The readers interested in a more rigorous discussion of differential forms are referred, for instance, to the book [22] of the bibliography. Let us finally notice that in this appendix we will follow the conventions introduced in Chap. 12, Sect. 12.1: latin letters a, b, c,...will denote Lorentz indices in the flat tangent space, Greek letters μ, ν, α,... tensor indices in the curved manifold. For the matter fields we will always use natural units = c = 1. Also, unless otherwise stated, in the first three Sects.
  • Minimally Separating Sets, Mediatrices, and Brillouin Spaces

    Minimally Separating Sets, Mediatrices, and Brillouin Spaces

    MINIMALLY SEPARATING SETS, MEDIATRICES, AND BRILLOUIN SPACES J.J.P. VEERMAN AND JAMES BERNHARD Abstract. Brillouin zones and their boundaries were studied in [16] because they play an important role in focal decomposition as first defined by Peixoto in [9] and in physics ([1] and [3]). In so-called Brillouin spaces, the boundaries of the Brillouin zones have certain regularity properties which imply that they consist of pieces of mediatrices (or equidistant sets). The purpose of this note is two-fold. First, we give some simple conditions on a metric space which are sufficient for it to be a Brillouin space. These con- ditions show, for example, that all compact, connected Riemannian manifolds with their usual distance functions are Brillouin spaces. Second, we exhibit a restriction on the Z2-homology of mediatrices in such manifolds in terms of the Z2-homology of the manifolds themselves, based on the fact that they are Bril- louin spaces. (This will used to obtain a classification up to homeomorphim of surface mediatrices in [15]). This note begins with some preliminaries in Section 1, where we define the relevant concepts and provide some background and motivation for the questions being considered here. In Section 2, we list a simple set of conditions on a metric space and prove that these conditions suffice for it to be a Brillouin space. In Section 3, we give some examples and mention a result for use in a later paper. We then investigate in Section 4 the homological restrictions placed on a mediatrix by the topology of the surrounding Brillouin space.