Feeder Routing for Air-To-Air Refueling Operations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

User Guide for the Envoy Data Link
User Guide for the Envoy Data Link SLC Doc Number UG-15000 Revision A 12335 134th Court NE Redmond, WA 98052 USA Tel: (425) 285-3000 Fax: (425) 285-4200 Email: [email protected] Preparer: Engineer: Program Manager: Quality Assurance: RESTRICTION ON USE, PUBLICATION, OR DISCLOSURE OF PROPRIETARY INFORMATION This document contains information proprietary to Spectralux Corporation, or to a third party to which Spectralux Corporation may have a legal obligation to protect such information from unauthorized disclosure, use, or duplication. Any disclosure, use, or duplication of this document or of any of the information contained herein for other than the specific purpose for which it was disclosed is expressly prohibited, except as Spectralux Corporation may otherwise agree to in writing. Spectralux™ Avionics Export Notice All information disclosed by Spectralux is to be considered United States (U.S.) origin technical data, and is export controlled. Accordingly, the receiving party is responsible for complying with all U.S. export regulations, including the U.S. Department of State International Traffic in Arms (ITAR), 22 CFR 120-130, and the U.S. Department of Commerce Export Administration Regulations (EAR), 15 CFR 730-774. Violations of these regulations are punishable by fine, imprisonment, or both. User Guide for the Envoy Data Link CHANGE RECORD APPROVAL/ PARAGRAPH DESCRIPTION OF CHANGE DATE REV Jenelle Anderson - All Initial Release July 31, 2019 All Updated with engineering feedback for terminology, implemented feeatured; Jenelle Anderson A deferred features are hidden. See ECO 15403 April 1, 2020 Document Number: UG-15000 Rev. A Page 2 of 173 User Guide for the Envoy Data Link TABLE OF CONTENTS 1 Introduction ........................................................................................................................... -

400 Hz September 2020 1 of 28
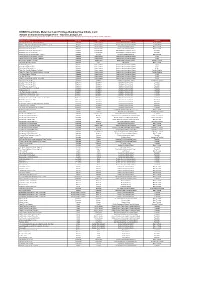
LIST OF REFERENCES ‐ 400 Hz September 2020 1 of 28 End‐user Segment Product Units Location Year Algiers Airport Airport 2400 ‐ 90 kVA 23 Algeria 2017 BOU‐SAÂDA Helicopter Hangar Airport 2300 ‐ 60 kVA 4 Algeria 2014 Air Algerie Airline 2400 ‐ 90 kVA 2 Algeria 2019 Air Algerie Airline 2400 ‐ 180 kVA 2 Algeria 2019 Protection civile Defence 2400 ‐ 30 kVA w/ARU 2 Algeria 2020 Protection civile Defence 2400 ‐ 30 kVA 2 Algeria 2019 Aerolineas Airline 2400 ‐ 60 kVA 1 Argentina 2020 Aerolineas Airline 2400 ‐ 30 kVA 1 Argentina 2016 Austral Airlines Airline 2400 ‐ 90 kVA 1 Argentina 2017 Brisbane Airport Airport 7400 ‐ 90 kVA 1 Australia 2018 Brisbane Airport Airport 2300 ‐ Power Coil 8 Australia 2013 Darwin Airport Airport 7400 ‐ 90 kVA 5 Australia 2019 Melbourne Airport Airport 2400 ‐ Power Coil 4 Australia 2018 Melbourne Airport Airport 2400 ‐ 90 kVA 9 Australia 2018 Melbourne Airport Airport 2400 ‐ Power Coil 2 Australia 2017 Melbourne Airport Airport 2400 ‐ 90 kVA 11 Australia 2014 Melbourne Airport Airport 2300 ‐ Power Coil 22 Australia 2011 Melbourne Airport Airport 2300 ‐ Power Coil 10 Australia 2011 Melbourne Airport Airport 2300 ‐ Power Coil 4 Australia 2009 Perth Airport Airport 2400 ‐ Power Coil 4 Australia 2017 Perth Airport Airport 2400 ‐ Power Coil 4 Australia 2017 Perth Airport Airport 2400 ‐ Power Coil 8 Australia 2017 Perth Airport Airport 2300 ‐ 90 kVA w/TRU 14 Australia 2013 Perth Airport Airport 2300 ‐ Power Coil 21 Australia 2013 Perth Airport Airport 2300 ‐ Power Coil 2 Australia 2013 Perth Airport Airport 2300 ‐ Power Coil -

ITW GSE Global LP References 25 May 2020 1400.Xlsm
LIST OF REFERENCES 28 VDC 25‐05‐2020 1 af 9 End‐user Segment Product Units Location Year BOU‐SAÂDA Helicopter Hangar Airport 28 VDC 3 Algeria 2014 Core, Inc. Maintenance 1400 ‐ 28 VDC 1 Argentina 2018 Adaptalift GSE Leasing Fleet Others 1400 ‐ 28 VDC 1 Australia rael Perth Airport Airport 2300 ‐ 90 kVA w/TRU 14 Australia 2013 Qantas Airways Airline 1400 ‐ 28 VDC 6 Australia 2019 QantasLink Airline 1400 ‐ 28 VDC 1 Australia 2019 Bartosch Airport Supply Maintenance 1400 ‐ 28 VDC 1 Austria 2019 Nassau Lynden Pindling International Airport Airport 2400 ‐ 90 kVA w/ARU 1 Bahamas 2015 MENA Aerospace Maintenance 1400 ‐ 28 VDC 1 Bahrain 2016 Biman Bangladesh Airlines Ltd. Airline 2400 ‐ 90 kVA w/ARU 1 Bangladesh 2016 TransStroy Mechanisation Others 1400 ‐ 28 VDC 6 Belarus 2018 Cofely Fabricom Others 1400 ‐ 28 VDC 1 Belgium 2015 Aero Rio Taxi Others 2400 ‐ 45 kVA w/ARU 1 Brazil 2016 Dassault Aircraft Aircraft manufacturer 1400 ‐ 28 VDC 1 Brazil 2019 Embraer Aircraft manufacturer 2400 ‐ 90 kVA w/ARU 5 Brazil 2016 Embraer Aircraft manufacturer 2400 ‐ 90 kVA w/ARU 2 Brazil 2015 Maga Aviation General Aviation 2400 ‐ 90 kVA w/ARU 1 Brazil 2017 Brunei Shell Petroleum Co. Others 1400 ‐ 28 VDC 1 Brunei 2020 Aero Technic BG Maintenance 2400 ‐ 90 kVA w/ARU 1 Bulgaria 2019 Aero Technic BG Maintenance 1400 ‐ 28 VDC 1 Bulgaria 2018 Aero Technic BG Maintenance 1400 ‐ 28 VDC 1 Bulgaria 2017 Quebec City Jean Lesage International Airport Airport 2400 ‐ 90 kVA w/ARU 1 Canada 2019 Quebec City Jean Lesage International Airport Airport 2400 ‐ 90 kVA w/ARU 5 Canada -

City/Airport Country IATA Codes
City/Airport Country IATA Codes Aarhus Denmark AAR Abadan Iran ABD Abeche Chad AEH Aberdeen United Kingdom ABZ Aberdeen (SD) USA ABR Abidjan Cote d'Ivoire ABJ Abilene (TX) USA ABI Abu Dhabi - Abu Dhabi International United Arab Emirates AUH Abuja - Nnamdi Azikiwe International Airport Nigeria ABV Abu Rudeis Egypt AUE Abu Simbel Egypt ABS Acapulco Mexico ACA Accra - Kotoka International Airport Ghana ACC Adana Turkey ADA Addis Ababa - Bole International Airport Ethiopia ADD Adelaide Australia ADL Aden - Aden International Airport Yemen ADE Adiyaman Turkey ADF Adler/Sochi Russia AER Agades Niger AJY Agadir Morocco AGA Agana (Hagåtña) Guam SUM Aggeneys South Africa AGZ Aguadilla Puerto Rico BQN Aguascaliente Mexico AGU Ahmedabad India AMD Aiyura Papua New Guinea AYU Ajaccio France AJA Akita Japan AXT Akron (OH) USA CAK Akrotiri - RAF Cyprus AKT Al Ain United Arab Emirates AAN Al Arish Egypt AAC Albany Australia ALH Albany (GA) USA ABY Albany (NY) - Albany International Airport USA ALB Albi France LBI Alborg Denmark AAL Albuquerque (NM) USA ABQ Albury Australia ABX Alderney Channel Islands ACI Aleppo Syria ALP Alesund Norway AES Alexander Bay - Kortdoorn South Africa ALJ Alexandria - Borg el Arab Airport Egypt HBH Alexandria - El Nhouza Airport Egypt ALY Alexandria - Esler Field USA (LA) ESF Alfujairah (Fujairah) United Arab Emirates FJR Alghero Sassari Italy AHO Algiers, Houari Boumediene Airport Algeria ALG Al Hoceima Morocco AHU Alicante Spain ALC Alice Springs Australia ASP Alldays South Africa ADY Allentown (PA) USA ABE Almaty (Alma -

Combined Bulletins Airport Bulletins
www.coltinternational.com Combined Bulletins Airport Bulletins UWPS | SKX | SARANSK Bulletin Type Start End Airport Slots May 1 2018 Jul 31 2018 Due to the Russia World Cup Slots are required starting May 1, 2018- July 31, 12:00 UTC 12:00 UTC 2018 General Jun 12 2018 Saransk Airport is an international airport in Mordovia located 7 km southeast of Information 12:00 UTC Saransk. It serves small airliners, but has undergone a major renovation in 2017 in time for the 2018 FIFA World Cup. City Bulletins Saransk, Russian Federation Bulletin Type Start End No Bulletins Country Bulletins Russian Federation Bulletin Type Start End CIQ Information Jun 30 2013 CIQ - Technical Stops 12:00 UTC When you make tech stops in Russia, depending upon the airport, it¶s possible that you may need to clear CIQ. For this reason it¶s best to confirm in advance such requirements, with your 3rd-party provider or ground handler. To avoid issues when making tech stops in Russia, passengers/crew members should have valid Russian visas. CIQ - New Regulations Please be informed that on the 30th of June 2013 the new Customs regulation of Russian Federation has been come into force. Accordinhg to this document criminal responsibility will be applied to the person illegal carrying available funds at the rate of 10 000 usd or more without official declaration. More information your passengers can find at official web-site of Russian Customs (unfortunately it is only in Russian at the moment): <http://www.customs.ru/index.php? option=com_content&view=article&id=17812:2013-07-03-05-42- 42&catid=40:2011-01-24-15-02-45&Itemid=2094&Itemid=1835>. -

City/Airport Country IATA Codes
City/Airport Country IATA Codes Aarhus Denmark AAR Abadan Iran ABD Abeche Chad AEH Aberdeen United Kingdom ABZ Aberdeen (SD) USA ABR Abidjan Cote d'Ivoire ABJ Abilene (TX) USA ABI Abu Dhabi - Abu Dhabi International United Arab Emirates AUH Abu Rudeis Egypt AUE Abu Simbel Egypt ABS Abuja - Nnamdi Azikiwe International Airport Nigeria ABV Acapulco Mexico ACA Accra - Kotoka International Airport Ghana ACC Adana Turkey ADA Addis Ababa - Bole International Airport Ethiopia ADD Adelaide Australia ADL Aden - Aden International Airport Yemen ADE Adiyaman Turkey ADF Adler/Sochi Russia AER Agades Niger AJY Agadir Morocco AGA Agana (Hagåtña) Guam SUM Aggeneys South Africa AGZ Aguadilla Puerto Rico BQN Aguascaliente Mexico AGU Ahmedabad India AMD Aiyura Papua New Guinea AYU Ajaccio France AJA Akita Japan AXT Akron (OH) USA CAK Akrotiri - RAF Cyprus AKT Al Ain United Arab Emirates AAN Al Arish Egypt AAC Al Hoceima Morocco AHU Albany Australia ALH Albany (GA) USA ABY Albany (NY) - Albany International Airport USA ALB Albi France LBI Alborg Denmark AAL Albuquerque (NM) USA ABQ Albury Australia ABX Alderney Channel Islands ACI Aleppo Syria ALP Alesund Norway AES Alexander Bay - Kortdoorn South Africa ALJ Alexandria - Esler Field USA (LA) ESF Alexandria - Borg el Arab Airport Egypt HBH Alexandria - El Nhouza Airport Egypt ALY Alfujairah (Fujairah) United Arab Emirates FJR Alghero Sassari Italy AHO Algiers, Houari Boumediene Airport Algeria ALG Alicante Spain ALC Alice Springs Australia ASP Alldays South Africa ADY Allentown (PA) USA ABE Almaty (Alma -

Evaluation of the Dynamic Characteristics of Aircraft During Landing in Crosswinds
DE GRUYTER OPEN Transport and Aerospace Engineering doi: 10.1515/tae-2015-0004 ________________________________________________________________________________________ 2015 / 2 Evaluation of the Dynamic Characteristics of Aircraft during Landing in Crosswinds Mareks Slihta1, Irina Lazareva2, Vladimirs Sestakovs3 1–3Institute of Aeronautics, Faculty of Transport and Mechanical Engineering, Riga Technical University Abstract – This article summarizes the results of aircraft lateral drift parameter estimation. The lateral drift of an aircraft may occur in extreme and dangerous situations when the aircraft lands in crosswind conditions. Such a situation is developing with great dynamics in a small period of time. Within seconds, the aircraft can drastically change the flight path or position. The article highlights the results obtained in a calculation made during the flight phase of the aircraft landing in crosswind. Keywords – Bank angle, crosswind, flight safety, tail fin. I. INTRODUCTION The flight of an aircraft can be considered successfully completed only when it has smoothly decelerated to a halt on the runway lane [1]. In practice, it can be seen that this is not always the case. Difficult and dangerous situations after touching the runway become accident factors in civil aviation. Most of them are “hard” landings of aircraft skid in outside the runway safety lanes [2]. The security lane is a specially prepared area along the runway and is intended for take-off and landing to ensure safety [3]. As a rule, “hard” landings end for -
Airport Companion by Dragonpass - Airport Lounge List *The List Is Subject to Change from Time to Time
UOBM Visa Infinite Metal Card and Privilege Banking Visa Infinite Card Airport Companion by DragonPass - Airport Lounge List *The list is subject to change from time to time. Please refer to the latest list in the Airport Companion by DragonPass mobile application. Airport Lounge Country City Airport Name Terminal Plaza Premium Lounge (Satellite Building) Malaysia Kuala Lumpur Kuala Lumpur International Airport KLIA Terminal Wellness Spa - Plaza Premium Lounge (KLIA2 - Level 3) Malaysia Kuala Lumpur Kuala Lumpur International Airport Terminal KLIA2 Plaza Premium Lounge (Domestic) Malaysia George Town Penang International Airport Main Terminal Plaza Premium Lounge (Int'l) Malaysia George Town Penang International Airport Main Terminal Plaza Premium Lounge (T1 Domestic) Malaysia Kota Kinabalu Kota Kinabalu International Airport Terminal 1 Plaza Premium Lounge (T1 Intl) Malaysia Kota Kinabalu Kota Kinabalu International Airport Terminal 1 Plaza Premium Lounge (Domestic - Level 2) Malaysia Kuching Kuching International Airport Main Terminal Plaza Premium Lounge (KLIA2 - Level 2) Malaysia Kuala Lumpur Kuala Lumpur International Airport KLIA2 Plaza Premium Lounge (KLIA2 - Landside) Malaysia Kuala Lumpur Kuala Lumpur International Airport KLIA2 Sky Lounge (Skypark Terminal) Malaysia Subang Jaya Sultan Abdul Aziz Shah Airport Skypark Terminal Miri Airport Executive Lounge Malaysia Miri Miri Airport Main Terminal KLIA Premier Access Malaysia Kuala Lumpur Kuala Lumpur International Airport KLIA Sama Sama Express KLIA Malaysia Kuala Lumpur Kuala -

GA Zprombank Group • ANNU AL REPOR T
GAZPROMBANK GROUP • ANNUAL REPORT 2016 FINANCIAL STATEMENTS FINANCIAL CONSOLIDATED IFRS ON BASED REPORT ANNUAL GROUP GAZPROMBANK GAZPROMBANK GROUP ANNUAL REPORT BASED ON IFRS CONSOLIDATED FINANCIAL STATEMENTS 3 GAZPROMBANK ANNUAL REPORT 2016 TABLE OF CONTENTS Statement of the Chairman of the Board of Directors 4 Statement of the Chairman of the Management Board 6 Key performance indicators 9 MAIN RESULTS FOR THE YEAR AND BUSINESS DEVELOPMENT OBJECTIVES 10 External environment in 2016 12 Financial performance 14 Positioning 18 Ratings 19 Business development strategy and objectives 20 SUSTAINABLE DEVELOPMENT 22 Corporate business Customer base 24 Commercial lending 28 Retail business Retail business 30 Private banking: 2016 full-year results and development prospects 34 Investment banking Project and structured finance 36 Most significant project finance and financial advice transactions in 2016 39 Commodity and capital market operations 40 Asset management 44 Privaty equity 45 Machine-building assets: principal areas of operations and key projects 47 Resource base development 48 Depository operations, specialized depository services 50 Risk management 51 Bank GPB (JSC) regional network 57 Regional network map 58 HR policy and employee development and motivation 60 Development of information technologies 63 Social responsibility and international cultural cooperation 64 CORPORATE GOVERNANCE 66 Shareholders of Bank GPB (JSC) 68 Board of Directors of Bank GPB (JSC) 69 Management Board of Bank GPB (JSC) 71 Corporate governance system of Bank -

Programme En.Pdf
30 November (Wednesday) Topic of the Day: #STRATEGY 10:00-11:00 Opening ceremony of the Forum and the Exhibition Coliseum Gostiny Dvor 11:00-11:30 Official tour across the exhibition Gostiny Dvor 11:30-12:00 Agreement and Memorandum Signing Ceremony Conference Hall No.3 Gostiny Dvor 11:30-12:00 Coffee break Catering Zone Gostiny Dvor 12:00-13:30 Open Discussion Led by Ministry of Transport of the Russian Federation Coliseum Business. Government. People Gostiny Dvor x Freight traffic. How to speed up transit traffic and provide equal-opportunity access to stevedoring services x Infrastructure. How “Platon” favours reconditioning of regional roads x Passenger traffic. How regional air travel is promoted and public transport fleet is renewed x Interaction. How to work with the updated composition of the State Duma x Safety and security. How to promote safety and security at transport infrastructure facilities and in vehicles Moderator: Evelina Zakamskaya, TV Presenter, Russia 24 Speakers: Maxim Sokolov, Minister of Transport, Russian Federation Evgeny Dietrich, First Deputy Minister of Transport, Russian Federation Sergey Aristov, State Secretary - Deputy Minister of Transport, Russian Federation Nikolay Asaul, Deputy Minister of Transport, Russian Federation Nikolay Zakhryapin, Deputy Minister of Transport, Russian Federation Valery Okulov, Deputy Minister of Transport, Russian Federation Viktor Olersky, Deputy Minister of Transport, Russian Federation - Head, Federal Marine and River Transport Agency Aleksey Tsydenov, Deputy Minister of Transport, Russian Federation Participants: Industry associations, social organizations, state administration bodies, higher education institutions 13:00-14:00 Lunch Catering Zone Gostiny Dvor 13:45-14:00 Celebrating the winners of Traffic Formula Awards Coliseum Gostiny Dvor 14:00-15:30 Plenary Session Coliseum Transport of Russia. -

Operating to 3M 64 12 11
Operating to THE 2018 FIFA WORLD CUP RUSSIA 3m 64 12 11 VISITORS MATCHES VENUES CITIES Russia will host the 2018 FIFA World Cup from June 14 - July 15. Three million visitors are expected to attend a total of 64 matches played at 12 venues in 11 cities with the opening ceremony and final taking place in Moscow. The World Cup will see a significant increase in traffic to many airports. It’s advisable for Operators to start planning immediately as massive congestion is expected at airports in the run-up to the competition. This guide will give you operational information such as permit requirements, visa considerations, and more for five gateways to Russia. | www.uas.aero Your Local Partner with global reach sm Operating to Russia Landing Permits Permit validity Landing permits are required in Russian Permits are valid from 0001 UTC from the airports. The following documentation is estimated time of arrival (ETA) and remain required: valid for an additional 48 hours as long as key information such as aircraft type, origin/ • Aircraft registration certificate destination airports and significant updates to • Airworthiness certificate the call-sign do not change. • Air Operator’s Certificate required to confirm flight category Additionally, for aircraft carrying fewer than 19 • Crew and passenger manifests passenger seats, no permit revision is needed for changes to entry/exit points into/from • Purpose of flight the Russian flight information region (FIR) or • Entry/exit points changes to the aerodrome of departure/landing • Route and schedule outside Russia • Aircraft insurance certificate that confirms worldwide insurance or specially naming Cabotage Russia and its territories, together with third- Foreign Operators are generally prohibited party liability details from conducting domestic flights in Russia without prior permission. -

KODY LOTNISK ICAO Niniejsze Zestawienie Zawiera 8372 Kody Lotnisk
KODY LOTNISK ICAO Niniejsze zestawienie zawiera 8372 kody lotnisk. Zestawienie uszeregowano: Kod ICAO = Nazwa portu lotniczego = Lokalizacja portu lotniczego AGAF=Afutara Airport=Afutara AGAR=Ulawa Airport=Arona, Ulawa Island AGAT=Uru Harbour=Atoifi, Malaita AGBA=Barakoma Airport=Barakoma AGBT=Batuna Airport=Batuna AGEV=Geva Airport=Geva AGGA=Auki Airport=Auki AGGB=Bellona/Anua Airport=Bellona/Anua AGGC=Choiseul Bay Airport=Choiseul Bay, Taro Island AGGD=Mbambanakira Airport=Mbambanakira AGGE=Balalae Airport=Shortland Island AGGF=Fera/Maringe Airport=Fera Island, Santa Isabel Island AGGG=Honiara FIR=Honiara, Guadalcanal AGGH=Honiara International Airport=Honiara, Guadalcanal AGGI=Babanakira Airport=Babanakira AGGJ=Avu Avu Airport=Avu Avu AGGK=Kirakira Airport=Kirakira AGGL=Santa Cruz/Graciosa Bay/Luova Airport=Santa Cruz/Graciosa Bay/Luova, Santa Cruz Island AGGM=Munda Airport=Munda, New Georgia Island AGGN=Nusatupe Airport=Gizo Island AGGO=Mono Airport=Mono Island AGGP=Marau Sound Airport=Marau Sound AGGQ=Ontong Java Airport=Ontong Java AGGR=Rennell/Tingoa Airport=Rennell/Tingoa, Rennell Island AGGS=Seghe Airport=Seghe AGGT=Santa Anna Airport=Santa Anna AGGU=Marau Airport=Marau AGGV=Suavanao Airport=Suavanao AGGY=Yandina Airport=Yandina AGIN=Isuna Heliport=Isuna AGKG=Kaghau Airport=Kaghau AGKU=Kukudu Airport=Kukudu AGOK=Gatokae Aerodrome=Gatokae AGRC=Ringi Cove Airport=Ringi Cove AGRM=Ramata Airport=Ramata ANYN=Nauru International Airport=Yaren (ICAO code formerly ANAU) AYBK=Buka Airport=Buka AYCH=Chimbu Airport=Kundiawa AYDU=Daru Airport=Daru