Big Data Analytics Lecture 2: Computation and Memory
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Management of Data Elements in Information Processing
PB-249-530 MANAGEMENT OF DATA ELEMENTS IN INFORMATION PROCESSING U.S. DEPARTMENT OF COMMERCE / National Bureau of Standards SECOND NATIONAL SYMPOSIUM NATIONAL BUREAU OF STANDARDS GAITHERSBURG, MARYLAND 1975 OCTOBER 23-24 Available by purchase from the National Technical Information Service, 5285 Port Royal Road, Springfield, Va. 221 Price: $9.25 hardcopy; $2.25 microfiche. National Technical Information Service U. S. DEPARTMENT OF COMMERCE PB-249-530 Management of Data Elements in Information Processing Proceedings of a Second Symposium Sponsored by the American National Standards Institute and by The National Bureau of Standards 1975 October 23-24 NBS, Gaithersburg, Maryland Hazel E. McEwen, Editor Institute for Computer Sciences and Technology National Bureau of Standards Washington, D.C. 20234 U.S. DEPARTMENT OF COMMERCE, Elliot L. Richardson, Secrefary NATIONAL BUREAU OF STANDARDS, Ernest Ambler, Acfing Direc/or Table of Contents Page Introduction to the Program of the Second National Symposium on The Management of Data Elements in Information Processing ix David V. Savidge, Program Chairman On-Line Tactical Data Inputting: Research in Operator Training and Performance 1 Irving Alderman, Ph.D. "Turning the Corner" on MIS, A Proposed Program of Data Standards in Post-Secondary Education 9 Donald R. Arnold, Ph.D. ASCII - The Data Alphabet That Will Endure 17 Robert W. Bemer Techniques in Developing Standard Procedures for Data Editing 23 George W. Covill An Adaptive File Management Systems 45 Dennis L. Dance and Udo W. Pooch (Given by Dance) A Focus on the Role of the Data Manager 57 Ruth M, Davis, Ph.D. A Proposed Standard Routine for Generating Proposed Standard Check Characters 61 Paul -Andre Desjardins Methodology for Development of Standard Data Elements within Multiple Public Agencies 69 L. -

H/W3 Binary to Denary
Name ___________________________________ Form ________ H/W Year 8 Homework Booklet Theme 1 Data Representation Computers themselves, and “ software yet to be developed, will revolutionize “ the way we learn. - Steve Jobs Founder of Apple Introduction What language does a computer understand? How does a computer represent data, information and images? Soon, you will be able to answer the questions above! In this theme we will explore the different ways in which data is represented by the computer, ranging from numbers to images. We will learn and understand the number bases and conversions between denary and binary. We will also be looking at units of information, binary addition and how we can convert binary data into a black and white image! See the key below to find out what the icons below mean: Self Assessment: You will mark your work at the start of next lesson. ENSURE YOU COMPELTE HOMEWORK AS MARKS WILL BE COLLECTED IN! Edmodo Quiz: The will be a quiz the start of next lesson based on your homework. SO MAKE SURE YOU REVISE! Peer Assessment: Homework marked by your class mate at the start of next lesson. MAKE SURE YOU HAVE YOUR HOMEWORK DONE SO YOU CAN SWAP WITH ANOTHER PUPIL! Stuck? Got a question? Email your teacher. Mr Rifai (Head of Computing) [email protected] Miss Davison [email protected] Miss Pascoe [email protected] 2 Due Date: H/W1 Data & Number Bases Read and digest the information below. You will be quizzed next lesson! Any set of characters gathered and translated for What is Data? some purpose. -

On Identifying Basic Discourse Units in Speech: Theoretical and Empirical Issues
Discours Revue de linguistique, psycholinguistique et informatique. A journal of linguistics, psycholinguistics and computational linguistics 4 | 2009 Linearization and Segmentation in Discourse On identifying basic discourse units in speech: theoretical and empirical issues Liesbeth Degand and Anne Catherine Simon Electronic version URL: http://journals.openedition.org/discours/5852 DOI: 10.4000/discours.5852 ISSN: 1963-1723 Publisher: Laboratoire LATTICE, Presses universitaires de Caen Electronic reference Liesbeth Degand and Anne Catherine Simon, « On identifying basic discourse units in speech: theoretical and empirical issues », Discours [Online], 4 | 2009, Online since 30 June 2009, connection on 10 December 2020. URL : http://journals.openedition.org/discours/5852 ; DOI : https://doi.org/ 10.4000/discours.5852 Discours est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d'Utilisation Commerciale - Pas de Modification 4.0 International. Discours 4 | 2009, Linearization and Segmentation in Discourse (Special issue) On identifying basic discourse units in speech: theoretical and empirical issues Liesbeth Degand1,2, Anne Catherine Simon2 1FNRS, 2Université catholique de Louvain Abstract: In spite of its crucial role in discourse segmentation and discourse interpretation, there is no consensus in the literature on what a discourse unit is and how it should be identified. Working with spoken data, we claim that the basic discourse unit (BDU) is a multi-dimensional unit that should be defined in terms of two linguistic criteria: prosody and syntax. In this paper, we explain which criteria are used to perform the prosodic and syntactic segmentation, and how these levels are mapped onto one another. We discuss three types BDUs (one-to-one, syntax-bound, prosody- bound) and open up a number of theoretical issues with respect to their function in discourse interpretation. -

Lecture Notes
CSCI E-84 A Practical Approach to Data Science Ramon A. Mata-Toledo, Ph.D. Professor of Computer Science Harvard University Unit 1 - Lecture 1 January, Wednesday 27, 2016 Required Textbooks Main Objectives of the Course This course is an introduction to the field of data science and its applicability to the business world. At the end of the semester you should be able to: • Understand how data science fits in an organization and gather, select, and model large amounts of data. • Identify the appropriate data and the methods that will allow you to extract knowledge from this data using the programming language R. What This Course is NOT is an in-depth calculus based statistic research environment . What is this course all about? It IS is a practical “hands-on approach” to understanding the methodology and tools of Data Science from a business prospective. Some of the technical we will briefly consider are: • Statistics • Database Querying • SQL • Data Warehousing • Regression Analysis • Explanatory versus Predictive Modeling Brief History of Data Science/Big Data The term data science can be considered the result of three main factors: • Evolution of data processing methods • Internet – particularly the Web 2.0 • Technological Advancements in computer processing speed/storage and development of algorithms for extracting useful information and knowledge from big data Brief History of Data Science/Big Data (continuation) However, “…Already seventy years ago we encounter the first attempts to quantify the growth rate in the volume of data or what has popularly been known as the “information explosion” (a term first used in 1941, according to the Oxford English Dictionary). -

Download Full Book
Introduction to Computing Explorations in Language, Logic, and Machines David Evans University of Virginia For the latest version of this book and supplementary materials, visit: http://computingbook.org Version: August 19, 2011 Attribution-Noncommercial-Share Alike 3.0 United States License Contents 1 Computing 1 1.1 Processes, Procedures, and Computers . 2 1.2 Measuring Computing Power . 3 1.2.1 Information . 3 1.2.2 Representing Data . 8 1.2.3 Growth of Computing Power . 12 1.3 Science, Engineering, and the Liberal Arts . 13 1.4 Summary and Roadmap . 16 Part I: Defining Procedures 2 Language 19 2.1 Surface Forms and Meanings . 19 2.2 Language Construction . 20 2.3 Recursive Transition Networks . 22 2.4 Replacement Grammars . 26 2.5 Summary . 32 3 Programming 35 3.1 Problems with Natural Languages . 36 3.2 Programming Languages . 37 3.3 Scheme . 39 3.4 Expressions . 40 3.4.1 Primitives . 40 3.4.2 Application Expressions . 41 3.5 Definitions . 44 3.6 Procedures . 45 3.6.1 Making Procedures . 45 3.6.2 Substitution Model of Evaluation . 46 3.7 Decisions . 48 3.8 Evaluation Rules . 50 3.9 Summary . 52 4 Problems and Procedures 53 4.1 Solving Problems . 53 4.2 Composing Procedures . 54 4.2.1 Procedures as Inputs and Outputs . 55 4.3 Recursive Problem Solving . 56 4.4 Evaluating Recursive Applications . 64 4.5 Developing Complex Programs . 67 4.5.1 Printing . 68 4.5.2 Tracing . 69 4.6 Summary . 73 5 Data 75 5.1 Types . 75 5.2 Pairs . -
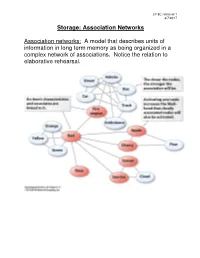
Storage: Association Networks Association Networks: a Model That
LP 8C retrieval 1 3/7/2017 Storage: Association Networks Association networks: A model that describes units of information in long term memory as being organized in a complex network of associations. Notice the relation to elaborative rehearsal. LP 8C retrieval 2 3/7/2017 Broken Associations Make Retrieval Difficult LP 8C retrieval 3 3/7/2017 Schemas and Encoding Schemas: Cognitive structures that help us perceive, organize, process and use information ( page 280). In the following example, a schema helps organize the seemingly random and obscure statements. Instructions: Take a minute to read through this paragraph. After a minute, try to recall as much information about the paragraph as you can. Do the best you can, exact word for word recall is not required as long as it is close. The procedure is actually quite simple. First arrange things into different groups. Of course, one pile may be sufficient depending on how much there is to do. If you have to go somewhere else due to lack of facilities that is the next step, otherwise you are pretty well set. It is important not to overdo things. That is, it is better to do too few things at once than too many. In the short run this may not seem important but complications can easily arise. A mistake can be expensive as well. At first, the whole procedure will seem complicated. Soon, however, it will become just another facet of life. It is difficult to foresee any end of the necessity for this task in the immediate future, but then one never can tell. -

Megabyte from Wikipedia, the Free Encyclopedia
Megabyte From Wikipedia, the free encyclopedia The megabyte is a multiple of the unit byte for digital information storage or transmission with two different values depending on context: 1 048 576 bytes (220) generally for computer memory;[1][2] and one million bytes (106, see prefix mega-) generally for computer storage.[1][3] The IEEE Standards Board has decided that "Mega will mean 1 000 000", with exceptions allowed for the base-two meaning.[3] In rare cases, it is used to mean 1000×1024 (1 024 000) bytes.[3] It is commonly abbreviated as Mbyte or MB (compare Mb, for the megabit). Multiples of bytes Contents SI decimal prefixes Binary IEC binary prefixes Name Value usage Name Value 1 Definition (Symbol) (Symbol) 2 Examples of use 3 10 10 3 See also kilobyte (kB) 10 2 kibibyte (KiB) 2 4 References megabyte (MB) 106 220 mebibyte (MiB) 220 5 External links gigabyte (GB) 109 230 gibibyte (GiB) 230 terabyte (TB) 1012 240 tebibyte (TiB) 240 Definition petabyte (PB) 1015 250 pebibyte (PiB) 250 exabyte (EB) 1018 260 exbibyte (EiB) 260 The term "megabyte" is commonly used to mean either zettabyte (ZB) 1021 270 zebibyte (ZiB) 270 10002 bytes or 10242 bytes. This originated as yottabyte (YB) 1024 280 yobibyte (YiB) 280 compromise technical jargon for the byte multiples that needed to be expressed by the powers of 2 but lacked See also: Multiples of bits · Orders of magnitude of data a convenient name. As 1024 (210) approximates 1000 (103), roughly corresponding SI multiples began to be used for binary multiples. -
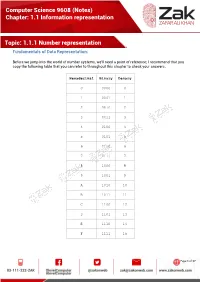
(Notes) Chapter: 1.1 Information Representation Topic
Computer Science 9608 (Notes) Chapter: 1.1 Information representation Topic: 1.1.1 Number representation Fundamentals of Data Representation: Before we jump into the world of number systems, we'll need a point of reference; I recommend that you copy the following table that you can refer to throughout this chapter to check your answers. Hexadecimal Binary Denary 0 0000 0 1 0001 1 2 0010 2 3 0011 3 4 0100 4 5 0101 5 6 0110 6 7 0111 7 8 1000 8 9 1001 9 A 1010 10 B 1011 11 C 1100 12 D 1101 13 E 1110 14 F 1111 15 Page 1 of 17 Computer Science 9608 (Notes) Chapter: 1.1 Information representation Topic: 1.1.1 Number representation Denary/Decimal Denary is the number system that you have most probably grown up with. It is also another way of saying base 10. This means that there are 10 different numbers that you can use for each digit, namely: 0,1,2,3,4,5,6,7,8,9 Notice that if we wish to say 'ten', we use two of the numbers from the above digits, 1 and 0. Thousands Hundreds Tens Units 10^3 10^2 10^1 10^0 1000 100 10 1 5 9 7 3 Using the above table we can see that each column has a different value assigned to it. And if we know the column values we can know the number, this will be very useful when we start looking at other base systems. Obviously, the number above is: five-thousands, nine-hundreds, seven-tens and three-units. -

1 Introduction to Informatics
1 Introduction to Informatics 1.1 Basics of Informatics Informatics is a very young scientific discipline and academic field. The interpretation of the term (in the sense used in modern European scientific literature) has not yet been established and generally accepted [1]. The homeland of most modern computers and computer technologies is located in the United States of America which is why American terminology in informatics is intertwined with that of Europe. The American term computer science is considered a synonym of the term informatics, but these two terms have a different history, somewhat different meanings, and are the roots of concept trees filled with different terminology. While a specialist in the field of computer science is called a computer engineer, a practitioner of informatics may be called an informatician. The history of the term computer science begins in the year 1959, when Louis Fein advocated the creation of the first Graduate School of Computer Science which would be similar to Harvard Business School. In justifying the name of the school, he referred to management science, which like computer science has an applied and interdisciplinary nature, and has characteristics of an academic discipline. Despite its name (computer science), most of the scientific areas related to the computer do not include the study of computers themselves. As a result, several alternative names have been proposed in the English speaking world, e.g., some faculties of major universities prefer the term computing science to emphasize the difference between the terms. Peter Naur suggested the Scandinavian term datalogy, to reflect the fact that the scientific discipline operates and handles data, although not necessarily with the use of computers. -

4 SCAP Messages for IF-M Specification
TCG Trusted Network Connect SCAP Messages for IF-M Specification Version 1.0 Revision 16 3 October 2012 Public Review Contact: Please submit comments by January 15, 2012 to scap-messages- [email protected] Review all comments received at: https://www.trustedcomputinggroup.org/resources/comments_for_tnc_scap_ messages_for_ifm Work in Progress This document is an intermediate draft for comment only and is subject to change without notice. Readers should not design products based on this document. TCG PUBLIC REVIEW TCG Copyright © TCG 2012 SCAP Messages for IF-M TCG Copyright Specification Version 1.0 Copyright © 2012 Trusted Computing Group, Incorporated. Disclaimer THIS SPECIFICATION IS PROVIDED "AS IS" WITH NO WARRANTIES WHATSOEVER, INCLUDING ANY WARRANTY OF MERCHANTABILITY, NONINFRINGEMENT, FITNESS FOR ANY PARTICULAR PURPOSE, OR ANY WARRANTY OTHERWISE ARISING OUT OF ANY PROPOSAL, SPECIFICATION OR SAMPLE. Without limitation, TCG disclaims all liability, including liability for infringement of any proprietary rights, relating to use of information in this specification and to the implementation of this specification, and TCG disclaims all liability for cost of procurement of substitute goods or services, lost profits, loss of use, loss of data or any incidental, consequential, direct, indirect, or special damages, whether under contract, tort, warranty or otherwise, arising in any way out of use or reliance upon this specification or any information herein. No license, express or implied, by estoppel or otherwise, to any TCG or TCG member intellectual property rights is granted herein. Except that a license is hereby granted by TCG to copy and reproduce this specification for internal use only. Contact the Trusted Computing Group at www.trustedcomputinggroup.org for information on specification licensing through membership agreements. -

Intermediate Notes
AQA Computer Science A-Level 4.5.3 Units of information Intermediate Notes www.pmt.education Specification: 4.5.3.1 Bits and bytes: Know that: ● the bit is the fundamental unit of information ● a byte is a group of 8 bits n Know that the 2 different values can be represented with n bits. 4.5.3.2 Units: Know that quantities of bytes can be described using binary prefixes representing powers of 2 or using decimal prefixes representing powers of 10 10, eg one kibibyte is written as 1KiB = 2 B and one kilobyte is written as 3 1kB = 10 B. Know the names, symbols and corresponding powers of 2 for the binary prefixes: ● kibi, Ki - 210 ● mebi, Mi - 220 ● gibi, Gi - 230 ● tebi, Ti - 240 Know the names, symbols and corresponding powers of 10 for the decimal prefixes: ● kilo, k - 103 ● mega, M - 106 ● giga, G - 109 ● tera, T - 1012 www.pmt.education Bits and bytes A bit can only take two values, 1 and 0. A group of 8 bits is called a byte. Half a byte (4 bits) is called a nybble. A bit is notated with a lowercase b whereas a byte uses a capital B. 2b = 2 bits 3B = 3 bytes = 3 * 8 bits = 24 bits The number of different values that can be represented with a specified number of bits varies with the number of bits. The more bits that are assigned to a number, the greater the number of values that can be represented. n More specifically, there are 2 different values that can be represented with n bits. -

Digital Computers in Nuclear Medicine
11 Digital Computers in Nuclear Medicine Digital computers were introduced in nuclear medicine practice in the mid- 1960s, but did not become an integral part in both imaging and nonimag- ing applications until the mid-1970s. In imaging modalities, the computers are used to quantitate the distribution of radiopharmaceuticals in an object both spatially and temporally. Both data acquisition and image processing in scintigraphy are accomplished by digital computers. In nonimaging appli- cations, patient scheduling, archiving, inventory of supplies, management of budget, record keeping, and health physics are just a few examples of what is accomplished with the help of digital computers. Computational capabil- ities have advanced tremendously over the years and are still evolving, and the utility of a computer is limited only by the limitations of hardware and software. Basics of a Computer The basic elements of a computer are a central processing unit (CPU), main memory, external storage and input/output (I/O) devices, which are con- nected to one another by pathways called buses. The main memory stores all program instructions and acquired data, while the CPU executes all instructions given in a program. External storage includes floppy disks, CD- ROMs, DVD-ROMs, and hard drives. I/O devices include peripherals such as keyboards, mouse, video monitors, and printers, whose functions are to communicate with the computer for input of the acquired data and output of the processed data. A typical setup of a computer is illustrated in Figure 11.1. The voltage signals, i.e., electrical pulses from a scintillation camera, are obtained in analog form and are digitized by the digital computers for further processing and storage.