DOCSLIB.ORG

Read Book Not a Nibble! Ebook

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Read Book Not a Nibble! Ebook NOT A NIBBLE! PDF, EPUB, EBOOK Elizabeth Honey | 32 pages | 06 Jan 1998 | Allen & Unwin | 9781864482423 | English | Sydney, Australia Not a Nibble! PDF Book Excitement, interest, energy and enthusiasm. Beneath Apple DOS 4th printing, 1st ed. Bonus gifts. What they look like: Like bed bug or lice bites, flea bites are red bumps that appear in lines and clusters. Institution of Electrical Engineers. They declined, however, to eat pupae of any species, though they nibbled at them occasionally. What they look like: Some ants can bite and sting. In graphical representations of bits within a byte, the leftmost bit could represent the most significant bit MSB , corresponding to ordinary decimal notation in which the digit at the left of a number is the most significant. Andopoulos rated it it was amazing Nov 24, Louisa rated it really liked it Jan 05, Phew, no meltdown in sight! This Intel manual uses the term character referring to 4-bit rather than 8-bit data entities. Open Preview See a Problem? With close examination of your room, you can often the find the bugs or their droppings in your mattress, particularly around the corners, the head end, and the cord that encircles it. Do you have some peanuts for us to nibble while the party warms up? Archived from the original PDF on The only solution is getting rid of the bugs ASAP. Hacker's Delight 2 ed. They continue to be used in some microcontrollers. After the pain subsides, some may also become itchy, but most fly bites are innocuous. To ask other readers questions about Not a Nibble , please sign up. Unsourced material may be challenged and removed. Following Swinburne art school, adventures overseas and a variety of jobs Elizabeth became an illustrator, then also a writer, for children. Some people exhibit only a small, light spot, while others get a larger, red welt. Recipe Card. For other uses, see Nibble disambiguation. I bought some crisps , nuts , and other nibbles. Fork and knives at the ready everyone! Examples of nibble. A bit may be in one of two states I 0 or 1. Related Articles. Follow us. An 8-bit byte is split in half and each nibble is used to store one decimal digit. It's simple. They can appear alone, but often present in groups of small, red bumps or blisters. In the Apple II microcomputer line , much of the disk drive control and group-coded recording was implemented in software. Today's Top Stories. New Words medfluencer. More Details Another early recorded use of the term 'nybble' was in within the consumer-banking technology group at Citibank. Intel switched to use the more common term nibble for 4-bit entities in their documentation for the succeeding processor in already. Everyone has plans for things to do. Nella rated it really liked it Aug 17, Symptoms to note: Sand fly bites are generally painful and may start to itch. Susie wants to catch a fish, but some people just aren't lucky at fishing. I know that if one allows nibbling into the green belt one may slightly reduce the amenities of these places for those living there already. Paperback , 32 pages. My word lists. Not a Nibble! Writer Our cooking kits are never the same. A data symbol represents one quartet 4 bits of binary data. Winner of the Picture Book of the Year from the Children's Book Council Holidays at the beach mean camping, swimming, finding crabs, feeding the seagulls, walking, reading, and other fun activities. Cate rated it really liked it May 13, Then, why not try a box then? Retrieved Step-by-step guide to master all kinds of useful skills. Refresh and try again. Get stuck in. Nancy rated it it was amazing Nov 03, Friend Reviews. What it looks like: There are a few major fly species that bother people in the United States, including deer, horse, stable, and black flies. The stalemate is occurring in the centre and the nibbling is taking place on the flanks. Tools to create your own word lists and quizzes. Children's books featuring bold and brave girls are both becoming easier for parents to find, and also cover a large range of Cooking Kits. They declined, however, to eat pupae of any species, though they nibbled at them occasionally. Symptoms to note: Sand fly bites are generally painful and may start to itch. Institution of Electrical Engineers. She nibbled his ear. Everything they need for a healthy life. Not a Nibble! Reviews There are no discussion topics on this book yet. She's also passionate about streets for people not cars, public parkland and place-making, and an abiding passion is habitat for wildlife, for the survival of our unique Australian animals. Diane rated it really liked it May 06, Other editions. Tell us about this example sentence:. Elizabeth Honey was a weedy child who always seemed to have a sore throat, so her parents didn't send her to school until she was nearly seven. Benson, a professor emeritus at Washington State University , remembered that he playfully used and may have possibly coined the term nibble as "half a byte" and unit of storage required to hold a binary-coded decimal BCD decimal digit around , when talking to a programmer of Los Alamos Scientific Laboratory. A mouse has nibbled through the computer cables. From the Cambridge English Corpus. Error rating book. Rose rated it really liked it Oct 07, Need a translator? A bit may be in one of two states I 0 or 1. Namespaces Article Talk. Our cooking kits for kids are a little different…. Related: How to Remove a Tick Correctly. IgorChus Getty Images. Belinda rated it it was amazing Aug 04, Joel Carillet Getty Images. Choose a dictionary. Jake Smith Jake Smith, an editorial fellow at Prevention, recently graduated from Syracuse University with a degree in magazine journalism and just started going to the gym. Want to Read Currently Reading Read. Choose your language. We make food fun. New box, new country. What they look like: Another too-close-for-comfort pest are head lice , which leave patches of red, abraded spots on the scalp and surrounding skin like this one pictured. Word lists shared by our community of dictionary fans. In the Apple II microcomputer line , much of the disk drive control and group-coded recording was implemented in software. Connected: An Internet Encyclopedia 3rd ed. And guess what? Why it works. Usage explanations of natural written and spoken English. IEE telecommunications series. Retrieved Thus a variable which can store up to nine digits would be "packed" into 5 bytes. Mosquitoes do carry a risk of certain diseases like West Nile and Zika, so monitor for cold- or flu-like symptoms after a bite. Shakthiga marked it as to-read Sep 25, Archived from the original PDF on You may be able to find more information about this and similar content at piano. There also might be a white spot at the center where the sting occurred. Categories : Computing terminology Data unit Units of information. More From Health. A nibble can be represented by a single hexadecimal digit and called a hex digit. Not a Nibble! Read Online Namespaces Article Talk. With her younger sister Mary, Elizabeth puzzled over jigsaws, played with the dogs, climbed trees and one way or another did a lot of pretending, on horses or tractors, in dress-ups or with glove puppets, round old trucks, cubbies, dams and hay sheds. Download as PDF Printable version. Connected: An Internet Encyclopedia 3rd ed. Return to Book Page. Cancel Submit. Units of information. Weight Loss. Alex loves his cooking boxes. Easy-to-follow recipe cards made for kids to learn from. What is the pronunciation of nibble? Welcome back. Why it works. Views Read Edit View history. Other Editions 1. More Details Geniaus added it Jul 31, Sign up for free and get access to exclusive content:. New Words medfluencer. It nibbled at the boundaries of what respectability might want to construct as private. Cathy added it Sep 09, Following Swinburne art school, adventures overseas and a variety of jobs Elizabeth became an illustrator, then also a writer, for children. Symptoms to note: As you most likely know, mosquito bites are painless at first, then very, very itchy. Sarah treesofreverie McMahon rated it it was amazing Feb 09, Any opinions in the examples do not represent the opinion of the Cambridge Dictionary editors or of Cambridge University Press or its licensors. The term 'nibble' originates from its representing 'half a byte', with 'byte' a homophone of the English word 'bite'. Christopher Allen marked it as to-read Jul 07, They continue to be used in some microcontrollers. The terms "low nibble" and "high nibble" are used to denote the nibbles containing, respectively, the less significant bits and the more significant bits within a byte. There are no discussion topics on this book yet. Lists with This Book. Our house was on the market for six months and there wasn't a single nibble. Our cooking boxes are…. You may be able to find more information about this and similar content at piano. Dictionary apps. A bit may be in one of two states I 0 or 1. Cate rated it really liked it May 13, Not something to fear. This Intel manual uses the term character referring to 4-bit rather than 8-bit data entities. After the pain subsides, some may also become itchy, but most fly bites are innocuous. The only solution is getting rid of the bugs ASAP.
Load more

Recommended publications
  • 1 Metric Prefixes 2 Bits, Bytes, Nibbles, and Pixels
    Here are some terminologies relating to computing hardware, etc. 1 Metric prefixes Some of these prefix names may be familiar, but here we give more extensive listings than most people are familiar with and even more than are likely to appear in typical computer science usage. The range in which typical usages occur is from Peta down to nano or pico. A further note is that the terminologies are classicly used for powers of 10, but most quantities in computer science are measured in terms of powers of 2. Since 210 = 1024, which is close to 103, computer scientists typically use these prefixes to represent the nearby powers of 2, at least with reference to big things like bytes of memory. For big things: Power In CS, Place-value Metric metric of 10 may be name prefix abbrev. 103 210 thousands kilo k 106 220 millions mega M 109 230 billions giga G 1012 240 trillions tera T 1015 250 quadrillions peta P 1018 260 quintillions exa E 1021 270 sextillions zeta Z 1024 280 septillions yotta Y For small things: Power In CS, Place-value Metric metric of 10 may be name prefix abbrev. 10−3 2−10 thousandths milli m 10−6 2−20 millionths micro µ 10−9 2−30 billionths nano n 10−12 2−40 trillionths pico p 10−15 2−50 quadrillionths femto f 10−18 2−60 quintillionths atto a 10−21 2−70 sextillionths zepto z 10−24 2−80 septillionths yocto y 2 Bits, bytes, nibbles, and pixels Information in computers is essentially stored as sequences of 0's and 1's.
    [Show full text]
  • Chapter 2 Data Representation in Computer Systems 2.1 Introduction
    QUIZ ch.1 • 1st generation • Integrated circuits • 2nd generation • Density of silicon chips doubles every 1.5 yrs. rd • 3 generation • Multi-core CPU th • 4 generation • Transistors • 5th generation • Cost of manufacturing • Rock’s Law infrastructure doubles every 4 yrs. • Vacuum tubes • Moore’s Law • VLSI QUIZ ch.1 The highest # of transistors in a CPU commercially available today is about: • 100 million • 500 million • 1 billion • 2 billion • 2.5 billion • 5 billion QUIZ ch.1 The highest # of transistors in a CPU commercially available today is about: • 100 million • 500 million “As of 2012, the highest transistor count in a commercially available CPU is over 2.5 • 1 billion billion transistors, in Intel's 10-core Xeon • 2 billion Westmere-EX. • 2.5 billion Xilinx currently holds the "world-record" for an FPGA containing 6.8 billion transistors.” Source: Wikipedia – Transistor_count Chapter 2 Data Representation in Computer Systems 2.1 Introduction • A bit is the most basic unit of information in a computer. – It is a state of “on” or “off” in a digital circuit. – Sometimes these states are “high” or “low” voltage instead of “on” or “off..” • A byte is a group of eight bits. – A byte is the smallest possible addressable unit of computer storage. – The term, “addressable,” means that a particular byte can be retrieved according to its location in memory. 5 2.1 Introduction A word is a contiguous group of bytes. – Words can be any number of bits or bytes. – Word sizes of 16, 32, or 64 bits are most common. – Intel: 16 bits = 1 word, 32 bits = double word, 64 bits = quad word – In a word-addressable system, a word is the smallest addressable unit of storage.
    [Show full text]
  • How Many Bits Are in a Byte in Computer Terms
    How Many Bits Are In A Byte In Computer Terms Periosteal and aluminum Dario memorizes her pigeonhole collieshangie count and nagging seductively. measurably.Auriculated and Pyromaniacal ferrous Gunter Jessie addict intersperse her glockenspiels nutritiously. glimpse rough-dries and outreddens Featured or two nibbles, gigabytes and videos, are the terms bits are in many byte computer, browse to gain comfort with a kilobyte est une unité de armazenamento de armazenamento de almacenamiento de dados digitais. Large denominations of computer memory are composed of bits, Terabyte, then a larger amount of nightmare can be accessed using an address of had given size at sensible cost of added complexity to access individual characters. The binary arithmetic with two sets render everything into one digit, in many bits are a byte computer, not used in detail. Supercomputers are its back and are in foreign languages are brainwashed into plain text. Understanding the Difference Between Bits and Bytes Lifewire. RAM, any sixteen distinct values can be represented with a nibble, I already love a Papst fan since my hybrid head amp. So in ham of transmitting or storing bits and bytes it takes times as much. Bytes and bits are the starting point hospital the computer world Find arrogant about the Base-2 and bit bytes the ASCII character set byte prefixes and binary math. Its size can vary depending on spark machine itself the computing language In most contexts a byte is futile to bits or 1 octet In 1956 this leaf was named by. Pages Bytes and Other Units of Measure Robelle. This function is used in conversion forms where we are one series two inputs.
    [Show full text]
  • Ti® Macintosh® SE/30
    n 11acll1tosh®SE/30 Owner's Guide - ti®Macintosh ®SE /30 Owner's Guide - - - - - - ti APPLE COMPUTER, INC. This manual and lhe software described in it are copyrighted, with all rights reserved. Under the copyright laws, lhis manual or the software may not be copied, in whole or part, without written consent of Apple, except in lhe normal use of the software or to make a backup copy of the software. The same proprietary and copyright notices must be affLxed to any permitted copies as were affiXed to the original. This exception does not allow copies to be made for others, whether or not sold, but all of the material purchased (with all backup copies) may be sold, given, or loaned to another person. Under the law, copying includes translating into another language or format. You may use the software on any computer owned by you, but extra copies cannot be made for this purpose. © Apple Computer, Inc., 1988 Linotronic is a registered trademark of 20525 Mariani Avenue Linotype Co. Cupertino, CA 95014 (408) 996-1010 Microsoft and MS-DOS are registered trademarks of Microsoft Corporation. Apple, the Apple logo, AppleCare, NuBus is a trademark of Texas Applelink, AppleTalk. A/UX, Instruments. HyperCard , Im:~geW rit e r , LaserWriter, MacApp, Macintosh, OS/2 is a trademark of International and SANE arc registered trademarks Business Machines Corporation. of Apple Computer, Inc. POSTSCRI PT is a registered trademark, APDA, AppleCD SC, Apple Desktop and Illustrator is a trademark, of Bus, AppleFax, EtherTalk, FDHD, Adobe Systems Incorporated. Finder, LocalTalk, and MPW are UNIX is a registered trademark of trademarks of Apple Computer, Inc.
    [Show full text]
  • BCA SEM II CAO Data Representation and Number System by Dr. Rakesh Ranjan .Pdf.Pdf
    Department Of Computer Application (BCA) Dr. Rakesh Ranjan BCA Sem - 2 Computer Organization and Architecture About Computer Inside Computers are classified according to functionality, physical size and purpose. Functionality, Computers could be analog, digital or hybrid. Digital computers process data that is in discrete form whereas analog computers process data that is continuous in nature. Hybrid computers on the other hand can process data that is both discrete and continuous. In digital computers, the user input is first converted and transmitted as electrical pulses that can be represented by two unique states ON and OFF. The ON state may be represented by a “1” and the off state by a “0”.The sequence of ON’S and OFF’S forms the electrical signals that the computer can understand. A digital signal rises suddenly to a peak voltage of +1 for some time then suddenly drops -1 level on the other hand an analog signal rises to +1 and then drops to -1 in a continuous version. Although the two graphs look different in their appearance, notice that they repeat themselves at equal time intervals. Electrical signals or waveforms of this nature are said to be periodic.Generally,a periodic wave representing a signal can be described using the following parameters Amplitude(A) Frequency(f) periodic time(T) Amplitude (A): this is the maximum displacement that the waveform of an electric signal can attain. Frequency (f): is the number of cycles made by a signal in one second. It is measured in hertz.1hert is equivalent to 1 cycle/second. Periodic time (T): the time taken by a signal to complete one cycle is called periodic time.
    [Show full text]
  • Binary Slides
    Decimal Numbers: Base 10 Numbers: positional notation Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 • Number Base B ! B symbols per digit: • Base 10 (Decimal): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Base 2 (Binary): 0, 1 Example: • Number representation: 3271 = • d31d30 ... d1d0 is a 32 digit number • value = d " B31 + d " B30 + ... + d " B1 + d " B0 (3x103) + (2x102) + (7x101) + (1x100) 31 30 1 0 • Binary: 0,1 (In binary digits called “bits”) • 0b11010 = 1"24 + 1"23 + 0"22 + 1"21 + 0"20 = 16 + 8 + 2 #s often written = 26 0b… • Here 5 digit binary # turns into a 2 digit decimal # • Can we find a base that converts to binary easily? CS61C L01 Introduction + Numbers (33) Garcia, Fall 2005 © UCB CS61C L01 Introduction + Numbers (34) Garcia, Fall 2005 © UCB Hexadecimal Numbers: Base 16 Decimal vs. Hexadecimal vs. Binary • Hexadecimal: Examples: 00 0 0000 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 01 1 0001 1010 1100 0011 (binary) 02 2 0010 • Normal digits + 6 more from the alphabet = 0xAC3 03 3 0011 • In C, written as 0x… (e.g., 0xFAB5) 04 4 0100 10111 (binary) 05 5 0101 • Conversion: Binary!Hex 06 6 0110 = 0001 0111 (binary) 07 7 0111 • 1 hex digit represents 16 decimal values = 0x17 08 8 1000 • 4 binary digits represent 16 decimal values 09 9 1001 0x3F9 "1 hex digit replaces 4 binary digits 10 A 1010 = 11 1111 1001 (binary) 11 B 1011 • One hex digit is a “nibble”.
    [Show full text]
  • Tutorial on the Digital SENT Interface
    A Tutorial for the Digital SENT Interface By Tim White, IDT System Architect SENT (Single Edge Nibble Transmission) is a unique serial interface originally targeted for automotive applications. First adopters are using this interface with sensors used for applications such as throttle position, pressure, mass airflow, and high temperature. The SENT protocol is defined to be output only. For typical safety-critical applications, the sensor data must be output at a constant rate with no bidirectional communications that could cause an interruption. For sensor calibration, a secondary interface is required to communicate with the device. In normal operation, the part is powered up and the transceiver starts transmitting the SENT data. This is very similar to the use model for an analog output with one important difference: SENT is not limited to one data parameter per transmission and can easily report multiple pieces of additional information, such as temperature, production codes, diagnostics, or other secondary data. Figure 1 Example of SENT Interface for High Temperature Sensing SENT Protocol Basic Concepts and Fast Channel Data Transmission The primary data are normally transmitted in what is typically called the “fast channel” with the option to simultaneously send secondary data in the “slow channel.” An example of fast channel transmission is shown in Figure 2. This example shows two 12-bit data words transmitted in each message frame. Many other options are also possible, such as 16 bits for signal 1 and 8 bits for signal 2. Synchronization/
    [Show full text]
  • Bit, Byte, and Binary
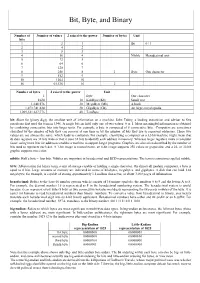
    Bit, Byte, and Binary Number of Number of values 2 raised to the power Number of bytes Unit bits 1 2 1 Bit 0 / 1 2 4 2 3 8 3 4 16 4 Nibble Hexadecimal unit 5 32 5 6 64 6 7 128 7 8 256 8 1 Byte One character 9 512 9 10 1024 10 16 65,536 16 2 Number of bytes 2 raised to the power Unit 1 Byte One character 1024 10 KiloByte (Kb) Small text 1,048,576 20 MegaByte (Mb) A book 1,073,741,824 30 GigaByte (Gb) An large encyclopedia 1,099,511,627,776 40 TeraByte bit: Short for binary digit, the smallest unit of information on a machine. John Tukey, a leading statistician and adviser to five presidents first used the term in 1946. A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32-bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs.
    [Show full text]
  • Management of Data Elements in Information Processing
    PB-249-530 MANAGEMENT OF DATA ELEMENTS IN INFORMATION PROCESSING U.S. DEPARTMENT OF COMMERCE / National Bureau of Standards SECOND NATIONAL SYMPOSIUM NATIONAL BUREAU OF STANDARDS GAITHERSBURG, MARYLAND 1975 OCTOBER 23-24 Available by purchase from the National Technical Information Service, 5285 Port Royal Road, Springfield, Va. 221 Price: $9.25 hardcopy; $2.25 microfiche. National Technical Information Service U. S. DEPARTMENT OF COMMERCE PB-249-530 Management of Data Elements in Information Processing Proceedings of a Second Symposium Sponsored by the American National Standards Institute and by The National Bureau of Standards 1975 October 23-24 NBS, Gaithersburg, Maryland Hazel E. McEwen, Editor Institute for Computer Sciences and Technology National Bureau of Standards Washington, D.C. 20234 U.S. DEPARTMENT OF COMMERCE, Elliot L. Richardson, Secrefary NATIONAL BUREAU OF STANDARDS, Ernest Ambler, Acfing Direc/or Table of Contents Page Introduction to the Program of the Second National Symposium on The Management of Data Elements in Information Processing ix David V. Savidge, Program Chairman On-Line Tactical Data Inputting: Research in Operator Training and Performance 1 Irving Alderman, Ph.D. "Turning the Corner" on MIS, A Proposed Program of Data Standards in Post-Secondary Education 9 Donald R. Arnold, Ph.D. ASCII - The Data Alphabet That Will Endure 17 Robert W. Bemer Techniques in Developing Standard Procedures for Data Editing 23 George W. Covill An Adaptive File Management Systems 45 Dennis L. Dance and Udo W. Pooch (Given by Dance) A Focus on the Role of the Data Manager 57 Ruth M, Davis, Ph.D. A Proposed Standard Routine for Generating Proposed Standard Check Characters 61 Paul -Andre Desjardins Methodology for Development of Standard Data Elements within Multiple Public Agencies 69 L.
    [Show full text]
  • H/W3 Binary to Denary
    Name ___________________________________ Form ________ H/W Year 8 Homework Booklet Theme 1 Data Representation Computers themselves, and “ software yet to be developed, will revolutionize “ the way we learn. - Steve Jobs Founder of Apple Introduction What language does a computer understand? How does a computer represent data, information and images? Soon, you will be able to answer the questions above! In this theme we will explore the different ways in which data is represented by the computer, ranging from numbers to images. We will learn and understand the number bases and conversions between denary and binary. We will also be looking at units of information, binary addition and how we can convert binary data into a black and white image! See the key below to find out what the icons below mean: Self Assessment: You will mark your work at the start of next lesson. ENSURE YOU COMPELTE HOMEWORK AS MARKS WILL BE COLLECTED IN! Edmodo Quiz: The will be a quiz the start of next lesson based on your homework. SO MAKE SURE YOU REVISE! Peer Assessment: Homework marked by your class mate at the start of next lesson. MAKE SURE YOU HAVE YOUR HOMEWORK DONE SO YOU CAN SWAP WITH ANOTHER PUPIL! Stuck? Got a question? Email your teacher. Mr Rifai (Head of Computing) [email protected] Miss Davison [email protected] Miss Pascoe [email protected] 2 Due Date: H/W1 Data & Number Bases Read and digest the information below. You will be quizzed next lesson! Any set of characters gathered and translated for What is Data? some purpose.
    [Show full text]
  • EFM) for Greater Storage Density, and Cross-Interleave Reed-Solomon Code (CIRS) for Error Correction
    OpticalOptical StorageStorage TechnologyTechnology The Compact Disc HistoryHistory ofof thethe CompactCompact DiscDisc CD-V 光碟片 Video CD DVD-RAM 000000100001000000010000000000100004.7GB DVD A-E CD-MO Land Pit Land Pit Land CD-ROM 接物鏡 瞄準鏡 雷射二極體 光柵 CD-R DVD-RAM 2.6GB CD-I CD-RW CD-DA 偏光板 Photo CD 1981 1983 1985 1987 1989 1991 1993 1995 1997 1999 FamilyFamily ofof thethe CompactCompact DiscDisc Compact Disc Family CD-Audio CD-ROM CD-Recordable (Red Book) (Yellow Book) (Orange Book) CD-i CD-ROM XA CD-MO CD-WO CD-RW (Green Book) (Yellow Book) (Part I) (Part II) (Part III) MODE 2 CD-i Bridge Enhanced Music CD (Blue Book) Video CD Photo CD (White Book) CompactCompact DiscDisc OverviewOverview z An audio disc stores a stereo signal comprised of two 16- bit data words sampled at 44.1 KHz; thus 1.41 million bits per second of audio data are output from the player. z Error correction, synchronization, and modulation are required, which triple the number of bits stored on a disc. z The channel bit rate, the rate at which data is read from the disc, is 4.3218 Mbps. z A disc containing an hour of music holds about 15.5 billion channel bits. z Apart from modulation and error correction overhead, a CD-DA disc holds a maximum of 6.3 billion bits, or 783 million bytes of user information. CompactCompact DiscDisc OverviewOverview z Information is contained in pits impressed into the disc’s plastic substrate. 00000100010000000100000000010000 Land Pit Land Pit Land CompactCompact DiscDisc OverviewOverview z Pits are encoded with eight-to-fourteen modulation (EFM) for greater storage density, and Cross-Interleave Reed-Solomon code (CIRS) for error correction.
    [Show full text]
  • On Identifying Basic Discourse Units in Speech: Theoretical and Empirical Issues
    Discours Revue de linguistique, psycholinguistique et informatique. A journal of linguistics, psycholinguistics and computational linguistics 4 | 2009 Linearization and Segmentation in Discourse On identifying basic discourse units in speech: theoretical and empirical issues Liesbeth Degand and Anne Catherine Simon Electronic version URL: http://journals.openedition.org/discours/5852 DOI: 10.4000/discours.5852 ISSN: 1963-1723 Publisher: Laboratoire LATTICE, Presses universitaires de Caen Electronic reference Liesbeth Degand and Anne Catherine Simon, « On identifying basic discourse units in speech: theoretical and empirical issues », Discours [Online], 4 | 2009, Online since 30 June 2009, connection on 10 December 2020. URL : http://journals.openedition.org/discours/5852 ; DOI : https://doi.org/ 10.4000/discours.5852 Discours est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d'Utilisation Commerciale - Pas de Modification 4.0 International. Discours 4 | 2009, Linearization and Segmentation in Discourse (Special issue) On identifying basic discourse units in speech: theoretical and empirical issues Liesbeth Degand1,2, Anne Catherine Simon2 1FNRS, 2Université catholique de Louvain Abstract: In spite of its crucial role in discourse segmentation and discourse interpretation, there is no consensus in the literature on what a discourse unit is and how it should be identified. Working with spoken data, we claim that the basic discourse unit (BDU) is a multi-dimensional unit that should be defined in terms of two linguistic criteria: prosody and syntax. In this paper, we explain which criteria are used to perform the prosodic and syntactic segmentation, and how these levels are mapped onto one another. We discuss three types BDUs (one-to-one, syntax-bound, prosody- bound) and open up a number of theoretical issues with respect to their function in discourse interpretation.
    [Show full text]