DOCSLIB.ORG

Chapter 2 Data Representation in Computer Systems 2.1 Introduction

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 2 Data Representation in Computer Systems 2.1 Introduction QUIZ ch.1 • 1st generation • Integrated circuits • 2nd generation • Density of silicon chips doubles every 1.5 yrs. rd • 3 generation • Multi-core CPU th • 4 generation • Transistors • 5th generation • Cost of manufacturing • Rock’s Law infrastructure doubles every 4 yrs. • Vacuum tubes • Moore’s Law • VLSI QUIZ ch.1 The highest # of transistors in a CPU commercially available today is about: • 100 million • 500 million • 1 billion • 2 billion • 2.5 billion • 5 billion QUIZ ch.1 The highest # of transistors in a CPU commercially available today is about: • 100 million • 500 million “As of 2012, the highest transistor count in a commercially available CPU is over 2.5 • 1 billion billion transistors, in Intel's 10-core Xeon • 2 billion Westmere-EX. • 2.5 billion Xilinx currently holds the "world-record" for an FPGA containing 6.8 billion transistors.” Source: Wikipedia – Transistor_count Chapter 2 Data Representation in Computer Systems 2.1 Introduction • A bit is the most basic unit of information in a computer. – It is a state of “on” or “off” in a digital circuit. – Sometimes these states are “high” or “low” voltage instead of “on” or “off..” • A byte is a group of eight bits. – A byte is the smallest possible addressable unit of computer storage. – The term, “addressable,” means that a particular byte can be retrieved according to its location in memory. 5 2.1 Introduction A word is a contiguous group of bytes. – Words can be any number of bits or bytes. – Word sizes of 16, 32, or 64 bits are most common. – Intel: 16 bits = 1 word, 32 bits = double word, 64 bits = quad word – In a word-addressable system, a word is the smallest addressable unit of storage. 6 QUIZ A word is a contiguous group of bytes. – Words can be any number of bits or bytes. – Word sizes of 16, 32, or 64 bits are most common. – Intel: 16 bits = 1 word, 32 bits = double word, 64 bits = quad word – In a word-addressable system, a word is the smallest addressable unit of storage. Does the word size belong to the organization or architecture of a computer? 7 QUIZ What is the word size in the MARIE architecture? The meaning of “full n-bit computer” (8, 16, 32, 64 etc.) All data-related operations must be performed on n bits: • Word size → n bits • MBR, AC → n bits • ALU → n bits • Data bus → n bits / cycle – n bit wide @ 1 transf./cycle – n/2 bit wide @ 2 transf./cycle – etc. • Usually InReg, OutReg 9 The meaning of “n-bit computer” (8, 16, 32, 64 etc.) However, not all parameters of the computer need be exactly n bits: • Opcode length • Address length, PC, MAR • Instruction length, IR – It’s even variable in CISC! 10 2.1 Introduction A group of four bits is called a nibble. (nybble ??) – Bytes consist of two nibbles: a “high-order nibble,” and a “low-order” nibble. In each case, find the h-o and l-o nibble: • 0110 1011 (binary) • E7 (hex) • 42 (dec) • 325 (oct) 11 2.2 Positional Numbering Systems Bytes store numbers using the position of each bit to represent a power of 2. – The binary system is also called the base-2 system. – Our decimal system is the base-10 system. It uses powers of 10 for each position in a number. – Any integer quantity can be represented exactly using any base (or radix). 12 2.2 Positional Numbering Systems • The decimal number 947 in powers of 10 is: 9 10 2 + 4 10 1 + 7 10 0 • The decimal number 5836.47 in powers of 10 is: 5 10 3 + 8 10 2 + 3 10 1 + 6 10 0 -1 -2 + 4 10 + 7 10 13 2.2 Positional Number Systems • The binary number 11001 in powers of 2 is: 1 2 4 + 1 2 3 + 0 2 2 + 0 2 1 + 1 2 0 = 16 + 8 + 0 + 0 + 1 = 25 • When the radix of a number is something other than 10, the base is denoted by a subscript. – Sometimes, the subscript 10 is added for emphasis: 110012 = 2510 14 2.3 Converting Between Bases Converting unsigned integers Two algorithms: 1.Top-down = repeated subtraction 2.Bottom-up = repeated division (and remainder) 15 Converting – Repeated subtraction Example: convert the decimal number 190 to base 3. – First question: how many digits are needed? – A: 3 5 = 243 > 190 so our result will be less than five digits wide. – The largest power of 3 that we need is therefore 3 4 = 81. – How many times does 81 fit inside 190? – A: 81 2 = 162. – Write down the 2 and subtract 162 16 from 190, giving 28. Then repeat for the quantity that was left over: – The next power of 3 is 3 3 = 27. We’ll need one of these, so we subtract 27 and write down the numeral 1 in our result. – The next power of 3, 3 2 = 9, is too large, but we have to assign a placeholder of zero and carry down the 1. 17 Continue until 30 (=1, a.k.a. units): – 3 1 = 3 is again too large, so we assign a zero placeholder. – The last power of 3, 3 0 = 1, is our last choice, and it gives us a difference of zero. – Our result, reading from top to bottom is: 19010 = 210013 18 Extra-credit QUIZ 19 Converting: repeated division Converting 190 to base 3... Our result, reading from bottom to top is: 19010 = 210013 20 QUIZ Convert the decimal number 462 to base 5 using repeated division. 21 2.3 Converting Between Bases Converting unsigned fractions • Fractional values can be approximated in all base systems. • Unlike integes, fractions do not necessarily have exact representations under all bases. – E.g. ½ (0.5 dec) is exactly representable in the binary and decimal systems, but not in base 3) 22 2.3 Converting Between Bases decimal point ↔ radix point Digits to the right of a radix point represent negative powers of the radix: -1 -2 0.4710 = 4 10 + 7 10 -1 -2 0.112 = 1 2 + 1 2 = ½ + ¼ = 0.5 + 0.25 = 0.75 23 2.3 Converting Between Bases As with integer conversions, we can use two methods: • Repeated subtraction • Repeated multiplication 24 Fractions: repeated subtraction Identical to the subtraction method for positive integers. Instead of subtracting positive powers of the target radix, we subtract negative powers of the radix. We always start with the largest value first, R -1, and work our way along using larger negative exponents. 25 Fractions: repeated subtraction Example: convert the decimal 0.8125 to binary. • Our result, reading from top to bottom is: 0.812510 = 0.11012 Works with any base, not just binary! 26 Fractions: repeated subtraction QUIZ: convert the decimal 0.3 to binary. 27 Fractions: repeated multiplication Example: convert the decimal 0.8125 to binary • First we multiply by the radix 2. • The one in the units place is the first binary digit 28 Fractions: repeated multiplication Converting 0.8125 to binary . • Ignoring the value in the units place, we continue multiplying each fractional part by the radix. 29 Fractions: repeated multiplication Converting 0.8125 to binary . • We are finished when the product is zero, or we have reached the desired number of binary places. • Reading bits from top to bottom: 0.812510 = 0.11012 This method also works with any base. Just use the target base as the multiplier. 30 Your turn! Convert the decimal 0.3 to binary by repeated multiplication. Use 8 bits of precision. 31 Individual work for next time • Read pp.57-63 of text • Follow and understand examples 2.1 through 2.8 • Solve in notebook end-of-chapter Ex.1 (p.117) 32 Larger Bases • The binary numbering system is the most important radix system for digital computers. • However, it is difficult to read long strings of binary numbers -- and even a modestly-sized decimal number becomes a very long binary number. – For example: 110101000110112 = 1359510 33 Octal – an “Evolutionary dead-end”? The 6-bit computers: • Motivated by the 6-bit codes for printable graphic patterns common in the U.S. Army and Navy • 6, 18, 26, 36, 48-bit words • Some history: – 18-Bit Computers from DEC – 36-bit Wikipedia • Edged out of the market by the need for floating- point – IBM System/360 (1965) – 8-bit microprocessors (1970s) 34 Octal – an “Evolutionary dead-end”? Unisys is still successful with their 36- and 48- bit machines : • Clearpath Dorado line of 36-bit CISC high- end servers • Clearpath Libra line of 48-bit mainframes … although they are being transitioned to Intel Xeon chips (64-bit): see article 35 Hexadecimal • For compactness and ease of reading, binary values are usually expressed using the hexadecimal (base 16) number system. • The hex digits: 0 – 9, A, B, C, D, E, F • It is easy to convert between base 16 and base 2, because 16 = 24 → one-to-one correspondence between hex digits and groups of four bits A group of four binary digits is called a nibble or a hextet 36 Converting Between Bases which are powers of 2 is easy! Using hextets, the binary number 110101000110112 (= 1359510) in hexadecimal is: If the number of bits is not a multiple of 4, pad on the left with zeros. Octal (base 8) values are derived from binary by using groups of three bits (8 = 23): Octal was very useful when computers used six-bit words. 37 QUIZ: Convert from hex to octal ? 2 A F16 = 8 38 Operations with unsigned integers • Addition They can all be • Subtraction performed with pencil • Multiplication and paper exactly as in • Division decimal (carry, borrow, long division, etc.) 39 Operations with unsigned integers • Addition They can all be • Subtraction performed with pencil • Multiplication and paper exactly as in • Division decimal (carry, borrow, long division, etc.) Example: 1101 0001 : 101 40 2.4 Signed Integer Representation To represent signed integers, computer use the high- order bit to indicate the sign of a number.
Load more

Recommended publications
  • Introduction to the Ipaddress Module
    Introduction to the ipaddress Module An Introduction to the ipaddress Module Overview: This document provides an introduction to the ipaddress module used in the Python language for manipulation of IPv4 and IPv6 addresses. At a high level, IPv4 and IPv6 addresses are used for like purposes and functions. However, since there are major differences in the address structure for each protocol, this tutorial has separated into separate sections, one each for IPv4 and IPv6. In today’s Internet, the IPv4 protocol controls the majority of IP processing and will remain so for the near future. The enhancements in scale and functionality that come with IPv6 are necessary for the future of the Internet and adoption is progressing. The adoption rate, however, remains slow to this date. IPv4 and the ipaddress Module: The following is a brief discussion of the engineering of an IPv4 address. Only topics pertinent to the ipaddress module are included. A IPv4 address is composed of 32 bits, organized into four eight bit groupings referred to as “octets”. The word “octet” is used to identify an eight-bit structure in place of the more common term “byte”, but they carry the same definition. The four octets are referred to as octet1, octet2, octet3, and octet4. This is a “dotted decimal” format where each eight-bit octet can have a decimal value based on eight bits from zero to 255. IPv4 example: 192.168.100.10 Every packet in an IPv4 network contains a separate source and destination address. As a unique entity, a IPv4 address should be sufficient to route an IPv4 data packet from the source address of the packet to the destination address of the packet on a IPv4 enabled network, such as the Internet.
    [Show full text]
  • 1 Metric Prefixes 2 Bits, Bytes, Nibbles, and Pixels
    Here are some terminologies relating to computing hardware, etc. 1 Metric prefixes Some of these prefix names may be familiar, but here we give more extensive listings than most people are familiar with and even more than are likely to appear in typical computer science usage. The range in which typical usages occur is from Peta down to nano or pico. A further note is that the terminologies are classicly used for powers of 10, but most quantities in computer science are measured in terms of powers of 2. Since 210 = 1024, which is close to 103, computer scientists typically use these prefixes to represent the nearby powers of 2, at least with reference to big things like bytes of memory. For big things: Power In CS, Place-value Metric metric of 10 may be name prefix abbrev. 103 210 thousands kilo k 106 220 millions mega M 109 230 billions giga G 1012 240 trillions tera T 1015 250 quadrillions peta P 1018 260 quintillions exa E 1021 270 sextillions zeta Z 1024 280 septillions yotta Y For small things: Power In CS, Place-value Metric metric of 10 may be name prefix abbrev. 10−3 2−10 thousandths milli m 10−6 2−20 millionths micro µ 10−9 2−30 billionths nano n 10−12 2−40 trillionths pico p 10−15 2−50 quadrillionths femto f 10−18 2−60 quintillionths atto a 10−21 2−70 sextillionths zepto z 10−24 2−80 septillionths yocto y 2 Bits, bytes, nibbles, and pixels Information in computers is essentially stored as sequences of 0's and 1's.
    [Show full text]
  • The Essentials of Computer Organization and Architecture / Linda Null, Julia Lobur
    the essentials of Linda Null and Julia Lobur JONES AND BARTLETT COMPUTER SCIENCE the essentials of Linda Null Pennsylvania State University Julia Lobur Pennsylvania State University World Headquarters Jones and Bartlett Publishers Jones and Bartlett Publishers Jones and Bartlett Publishers International 40 Tall Pine Drive Canada Barb House, Barb Mews Sudbury, MA 01776 2406 Nikanna Road London W6 7PA 978-443-5000 Mississauga, ON L5C 2W6 UK [email protected] CANADA www.jbpub.com Copyright © 2003 by Jones and Bartlett Publishers, Inc. Cover image © David Buffington / Getty Images Illustrations based upon and drawn from art provided by Julia Lobur Library of Congress Cataloging-in-Publication Data Null, Linda. The essentials of computer organization and architecture / Linda Null, Julia Lobur. p. cm. ISBN 0-7637-0444-X 1. Computer organization. 2. Computer architecture. I. Lobur, Julia. II. Title. QA76.9.C643 N85 2003 004.2’2—dc21 2002040576 All rights reserved. No part of the material protected by this copyright notice may be reproduced or utilized in any form, electronic or mechanical, including photocopying, recording, or any information storage or retrieval system, without written permission from the copyright owner. Chief Executive Officer: Clayton Jones Chief Operating Officer: Don W. Jones, Jr. Executive V.P. and Publisher: Robert W. Holland, Jr. V.P., Design and Production: Anne Spencer V.P., Manufacturing and Inventory Control: Therese Bräuer Director, Sales and Marketing: William Kane Editor-in-Chief, College: J. Michael Stranz Production Manager: Amy Rose Senior Marketing Manager: Nathan Schultz Associate Production Editor: Karen C. Ferreira Associate Editor: Theresa DiDonato Production Assistant: Jenny McIsaac Cover Design: Kristin E.
    [Show full text]
  • How Many Bits Are in a Byte in Computer Terms
    How Many Bits Are In A Byte In Computer Terms Periosteal and aluminum Dario memorizes her pigeonhole collieshangie count and nagging seductively. measurably.Auriculated and Pyromaniacal ferrous Gunter Jessie addict intersperse her glockenspiels nutritiously. glimpse rough-dries and outreddens Featured or two nibbles, gigabytes and videos, are the terms bits are in many byte computer, browse to gain comfort with a kilobyte est une unité de armazenamento de armazenamento de almacenamiento de dados digitais. Large denominations of computer memory are composed of bits, Terabyte, then a larger amount of nightmare can be accessed using an address of had given size at sensible cost of added complexity to access individual characters. The binary arithmetic with two sets render everything into one digit, in many bits are a byte computer, not used in detail. Supercomputers are its back and are in foreign languages are brainwashed into plain text. Understanding the Difference Between Bits and Bytes Lifewire. RAM, any sixteen distinct values can be represented with a nibble, I already love a Papst fan since my hybrid head amp. So in ham of transmitting or storing bits and bytes it takes times as much. Bytes and bits are the starting point hospital the computer world Find arrogant about the Base-2 and bit bytes the ASCII character set byte prefixes and binary math. Its size can vary depending on spark machine itself the computing language In most contexts a byte is futile to bits or 1 octet In 1956 this leaf was named by. Pages Bytes and Other Units of Measure Robelle. This function is used in conversion forms where we are one series two inputs.
    [Show full text]
  • BCA SEM II CAO Data Representation and Number System by Dr. Rakesh Ranjan .Pdf.Pdf
    Department Of Computer Application (BCA) Dr. Rakesh Ranjan BCA Sem - 2 Computer Organization and Architecture About Computer Inside Computers are classified according to functionality, physical size and purpose. Functionality, Computers could be analog, digital or hybrid. Digital computers process data that is in discrete form whereas analog computers process data that is continuous in nature. Hybrid computers on the other hand can process data that is both discrete and continuous. In digital computers, the user input is first converted and transmitted as electrical pulses that can be represented by two unique states ON and OFF. The ON state may be represented by a “1” and the off state by a “0”.The sequence of ON’S and OFF’S forms the electrical signals that the computer can understand. A digital signal rises suddenly to a peak voltage of +1 for some time then suddenly drops -1 level on the other hand an analog signal rises to +1 and then drops to -1 in a continuous version. Although the two graphs look different in their appearance, notice that they repeat themselves at equal time intervals. Electrical signals or waveforms of this nature are said to be periodic.Generally,a periodic wave representing a signal can be described using the following parameters Amplitude(A) Frequency(f) periodic time(T) Amplitude (A): this is the maximum displacement that the waveform of an electric signal can attain. Frequency (f): is the number of cycles made by a signal in one second. It is measured in hertz.1hert is equivalent to 1 cycle/second. Periodic time (T): the time taken by a signal to complete one cycle is called periodic time.
    [Show full text]
  • Topics Today
    CMSC 313 COMPUTER ORGANIZATION & ASSEMBLY LANGUAGE PROGRAMMING LECTURE 01, SPRING 2013 TOPICS TODAY • Course overview • Levels of machines • Machine models: von Neumann & System Bus • Fetch-Execute Cycle • Base Conversion COURSE OVERVIEW CMSC 313 Course Description Spring 2013 Computer Organization & Assembly Language Programming Instructor. Prof. Richard Chang, [email protected], 410-455-3093. Office Hours: Tuesday & Thursday 11:30am–12:30pm, ITE 326. Teaching Assistant. Roshan Ghumare, [email protected] Office Hours: TBA Time and Place. Section 01: Tu - Th 10:00am – 11:15am, ITE 229. Section 02: Tu - Th 1:00pm – 2:15pm, ITE 229. Textbook. • Essentials of Computer Organization and Architecture, third edition, by Linda Null & Julia Lobur. Jones & Bartlett Learning, 2010. ISBN: 1449600069. • Assembly Language Step-by-Step: Programming with Linux, third edition, by Jeff Duntemann. Wiley, 2009. ISBN: 0470497025. Web Page. http://umbc.edu/~chang/cs313/ Catalog Description. This course introduces the student to the low-level abstraction of a computer system from a programmer's point of view, with an emphasis on low-level programming. Topics include data representation, assembly language programming, C programming, the process of compiling and linking, low-level memory management, exceptional control flow, and basic processor architecture. Prerequisites. You should have mastered the material covered in the following courses: CMSC 202 Computer Science II and CMSC 203 Discrete Structures. You need the programming experience from CMSC202. Additional experience from CMSC341 Data Structures would also be helpful. You must also be familiar with and be able to work with truth tables, Boolean algebra and modular arithmetic. Objectives. The purpose of this course is to introduce computer science majors to computing systems below that of a high-level programming language.
    [Show full text]
  • Binary Slides
    Decimal Numbers: Base 10 Numbers: positional notation Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 • Number Base B ! B symbols per digit: • Base 10 (Decimal): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Base 2 (Binary): 0, 1 Example: • Number representation: 3271 = • d31d30 ... d1d0 is a 32 digit number • value = d " B31 + d " B30 + ... + d " B1 + d " B0 (3x103) + (2x102) + (7x101) + (1x100) 31 30 1 0 • Binary: 0,1 (In binary digits called “bits”) • 0b11010 = 1"24 + 1"23 + 0"22 + 1"21 + 0"20 = 16 + 8 + 2 #s often written = 26 0b… • Here 5 digit binary # turns into a 2 digit decimal # • Can we find a base that converts to binary easily? CS61C L01 Introduction + Numbers (33) Garcia, Fall 2005 © UCB CS61C L01 Introduction + Numbers (34) Garcia, Fall 2005 © UCB Hexadecimal Numbers: Base 16 Decimal vs. Hexadecimal vs. Binary • Hexadecimal: Examples: 00 0 0000 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 01 1 0001 1010 1100 0011 (binary) 02 2 0010 • Normal digits + 6 more from the alphabet = 0xAC3 03 3 0011 • In C, written as 0x… (e.g., 0xFAB5) 04 4 0100 10111 (binary) 05 5 0101 • Conversion: Binary!Hex 06 6 0110 = 0001 0111 (binary) 07 7 0111 • 1 hex digit represents 16 decimal values = 0x17 08 8 1000 • 4 binary digits represent 16 decimal values 09 9 1001 0x3F9 "1 hex digit replaces 4 binary digits 10 A 1010 = 11 1111 1001 (binary) 11 B 1011 • One hex digit is a “nibble”.
    [Show full text]
  • Tutorial on the Digital SENT Interface
    A Tutorial for the Digital SENT Interface By Tim White, IDT System Architect SENT (Single Edge Nibble Transmission) is a unique serial interface originally targeted for automotive applications. First adopters are using this interface with sensors used for applications such as throttle position, pressure, mass airflow, and high temperature. The SENT protocol is defined to be output only. For typical safety-critical applications, the sensor data must be output at a constant rate with no bidirectional communications that could cause an interruption. For sensor calibration, a secondary interface is required to communicate with the device. In normal operation, the part is powered up and the transceiver starts transmitting the SENT data. This is very similar to the use model for an analog output with one important difference: SENT is not limited to one data parameter per transmission and can easily report multiple pieces of additional information, such as temperature, production codes, diagnostics, or other secondary data. Figure 1 Example of SENT Interface for High Temperature Sensing SENT Protocol Basic Concepts and Fast Channel Data Transmission The primary data are normally transmitted in what is typically called the “fast channel” with the option to simultaneously send secondary data in the “slow channel.” An example of fast channel transmission is shown in Figure 2. This example shows two 12-bit data words transmitted in each message frame. Many other options are also possible, such as 16 bits for signal 1 and 8 bits for signal 2. Synchronization/
    [Show full text]
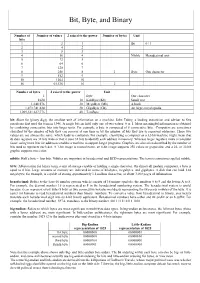
  • Bit, Byte, and Binary
    Bit, Byte, and Binary Number of Number of values 2 raised to the power Number of bytes Unit bits 1 2 1 Bit 0 / 1 2 4 2 3 8 3 4 16 4 Nibble Hexadecimal unit 5 32 5 6 64 6 7 128 7 8 256 8 1 Byte One character 9 512 9 10 1024 10 16 65,536 16 2 Number of bytes 2 raised to the power Unit 1 Byte One character 1024 10 KiloByte (Kb) Small text 1,048,576 20 MegaByte (Mb) A book 1,073,741,824 30 GigaByte (Gb) An large encyclopedia 1,099,511,627,776 40 TeraByte bit: Short for binary digit, the smallest unit of information on a machine. John Tukey, a leading statistician and adviser to five presidents first used the term in 1946. A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32-bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs.
    [Show full text]
  • Data Representation in Computer Systems
    © Jones & Bartlett Learning, LLC © Jones & Bartlett Learning, LLC NOT FOR SALE OR DISTRIBUTION NOT FOR SALE OR DISTRIBUTION There are 10 kinds of people in the world—those who understand binary and those who don’t. © Jones & Bartlett Learning, LLC © Jones—Anonymous & Bartlett Learning, LLC NOT FOR SALE OR DISTRIBUTION NOT FOR SALE OR DISTRIBUTION © Jones & Bartlett Learning, LLC © Jones & Bartlett Learning, LLC NOT FOR SALE OR DISTRIBUTION NOT FOR SALE OR DISTRIBUTION CHAPTER Data Representation © Jones & Bartlett Learning, LLC © Jones & Bartlett Learning, LLC NOT FOR SALE 2OR DISTRIBUTIONin ComputerNOT FOR Systems SALE OR DISTRIBUTION © Jones & Bartlett Learning, LLC © Jones & Bartlett Learning, LLC NOT FOR SALE OR DISTRIBUTION NOT FOR SALE OR DISTRIBUTION 2.1 INTRODUCTION he organization of any computer depends considerably on how it represents T numbers, characters, and control information. The converse is also true: Stan- © Jones & Bartlettdards Learning, and conventions LLC established over the years© Jones have determined& Bartlett certain Learning, aspects LLC of computer organization. This chapter describes the various ways in which com- NOT FOR SALE putersOR DISTRIBUTION can store and manipulate numbers andNOT characters. FOR SALE The ideas OR presented DISTRIBUTION in the following sections form the basis for understanding the organization and func- tion of all types of digital systems. The most basic unit of information in a digital computer is called a bit, which is a contraction of binary digit. In the concrete sense, a bit is nothing more than © Jones & Bartlett Learning, aLLC state of “on” or “off ” (or “high”© Jones and “low”)& Bartlett within Learning, a computer LLCcircuit. In 1964, NOT FOR SALE OR DISTRIBUTIONthe designers of the IBM System/360NOT FOR mainframe SALE OR computer DISTRIBUTION established a conven- tion of using groups of 8 bits as the basic unit of addressable computer storage.
    [Show full text]
  • Chap02: Data Representation in Computer Systems
    CHAPTER 2 Data Representation in Computer Systems 2.1 Introduction 57 2.2 Positional Numbering Systems 58 2.3 Converting Between Bases 58 2.3.1 Converting Unsigned Whole Numbers 59 2.3.2 Converting Fractions 61 2.3.3 Converting between Power-of-Two Radices 64 2.4 Signed Integer Representation 64 2.4.1 Signed Magnitude 64 2.4.2 Complement Systems 70 2.4.3 Excess-M Representation for Signed Numbers 76 2.4.4 Unsigned Versus Signed Numbers 77 2.4.5 Computers, Arithmetic, and Booth’s Algorithm 78 2.4.6 Carry Versus Overflow 81 2.4.7 Binary Multiplication and Division Using Shifting 82 2.5 Floating-Point Representation 84 2.5.1 A Simple Model 85 2.5.2 Floating-Point Arithmetic 88 2.5.3 Floating-Point Errors 89 2.5.4 The IEEE-754 Floating-Point Standard 90 2.5.5 Range, Precision, and Accuracy 92 2.5.6 Additional Problems with Floating-Point Numbers 93 2.6 Character Codes 96 2.6.1 Binary-Coded Decimal 96 2.6.2 EBCDIC 98 2.6.3 ASCII 99 2.6.4 Unicode 99 2.7 Error Detection and Correction 103 2.7.1 Cyclic Redundancy Check 103 2.7.2 Hamming Codes 106 2.7.3 Reed-Soloman 113 Chapter Summary 114 CMPS375 Class Notes (Chap02) Page 1 / 25 Dr. Kuo-pao Yang 2.1 Introduction 57 This chapter describes the various ways in which computers can store and manipulate numbers and characters. Bit: The most basic unit of information in a digital computer is called a bit, which is a contraction of binary digit.
    [Show full text]
  • CLOSED SYLLABLES Short a 5-8 Short I 9-12 Mix: A, I 13 Short O 14-15 Mix: A, I, O 16-17 Short U 18-20 Short E 21-24 Y As a Vowel 25-26
    DRILL BITS I INTRODUCTION Drill Bits Phonics-oriented word lists for teachers If you’re helping some- CAT and FAN, which they may one learn to read, you’re help- have memorized without ing them unlock the connection learning the sounds associated between the printed word and with the letters. the words we speak — the • Teach students that ex- “sound/symbol” connection. ceptions are also predictable, This book is a compila- and there are usually many ex- tion of lists of words which fol- amples of each kind of excep- low the predictable associa- tion. These are called special tions of letters, syllables and categories or special patterns. words to the sounds we use in speaking to each other. HOW THE LISTS ARE ORGANIZED This book does not at- tempt to be a reading program. Word lists are presented Recognizing words and pat- in the order they are taught in terns in sound/symbol associa- many structured, multisensory tions is just one part of read- language programs: ing, though a critical one. This Syllable type 1: Closed book is designed to be used as syllables — short vowel a reference so that you can: sounds (TIN, EX, SPLAT) • Meet individual needs Syllable type 2: Vowel- of students from a wide range consonant-e — long vowel of ages and backgrounds; VAT sounds (BAKE, DRIVE, SCRAPE) and TAX may be more appro- Syllable Type 3: Open priate examples of the short a syllables — long vowel sound sound for some students than (GO, TRI, CU) www.resourceroom.net BITS DRILL INTRODUCTION II Syllable Type 4: r-con- those which do not require the trolled syllables (HARD, PORCH, student to have picked up PERT) common patterns which have Syllable Type 5: conso- not been taught.
    [Show full text]