DOCSLIB.ORG

Functional Programming in Scheme and Lisp

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Functional Programming in Scheme and Lisp Functional Programming in Scheme and Lisp http://www.lisperati.com/landoflisp/ Overview eval • Remember: Lisp code is just an s-expression • In a functional programming language, functions are first class objects • You can call Lisp’s evaluation process with the eval function • You can create them, put them in data structures, compose them, specialize them, > (define s (list 'cadr ' ' (one two three))) apply them to arguments, etc. > s (cadr ' (one two three)) • We’ll look at how functional programming things are done in Lisp > (eval s) two > (eval (list 'cdr (car '((quote (a . b)) c)))) b apply lambda • apply takes a function & a list of arguments for it & returns the result of applying the function to them • The define special form creates a function and > (apply + ' (1 2 3)) gives it a name 6 • However, functions don’t have to have names, • It can be given any number of arguments, so long as and we don’t need to use define to create the last is a list: them > (apply + 1 2 ' (3 4 5)) • The primitive way to create functions is to use 15 the lambda special form • A simple version of apply could be written as (define (apply f list) (eval (cons f list))) • These are often called lambda expressions, e.g. (lambda (x) (+ x 1)) 1 lambda expression Lambda expression • lambda is a special form • A lambda expression is a list of the symbol • When evaluated, it creates a function and lambda, followed by a list of parameters, fol- returns a reference to it lowed by a body of one or more expressions: • The function does not have a name > (define f (lambda (x) (+ x 2))) • A lambda expression can be the first ele- > f ment of a function call: #<proceedure:f> > ( (lambda (x) (+ x 100)) 1) > (f 100) 101 • Other languages like python and javascript 102 have adopted the idea > ( (lambda (x) (+ x 2)) 100) 102 define vs. define Functions as objects (define (add2 x) • The define special form • While many PLs allow functions as (+ x 2) ) comes in two varieties arguments, nameless lambda functions • The three expressions to add flexibility (define add2 the right are entirely (lambda (x) (+ x 2))) equivalent > (sort '((a 100)(b 10)(c 50)) • The first define form is (lambda (x y) (< (second x) (second y)))) (define add2 #f) just more familiar and ((b 10) (c 50) (a 100)) convenient when defining (set! add2 • There is no need to give the function a (lambda (x) (+ x 2))) a function name lambdas in other languages Mapping functions • Lisp & Scheme have several mapping functions • Lambda expressions are found in many • map (mapcar in Lisp) is the most useful modern languages, e.g., Python: • It takes a function and ≥1 lists and returns a list >>> f = lambda x,y: x*x + y of the results of applying the function to elements taken from each list >>> f > (map abs '(3 -4 2 -5 -6)) <function <lambda> at 0x10048a230> (3 4 2 5 6) >>> f(2, 3) > (map + ‘(1 2 3) (4 5 6)) 7 (5 7 9) >>> (lambda x,y: x*x+y)(2,3) > (map + ‘(1 2 3) ‘(4 5 6) ‘(7 8 9)) 7 (12 15 18) 2 More map examples Defining map > (map cons '(a b c) '(1 2 3)) Defining a simple “one argument” version of ((a . 1) (b . 2) (c . 3)) map is easy > (map (lambda (x) (+ x 10)) ‘(1 2 3)) (define (map1 func list) (11 12 13) (if (null? list) > (map + '(1 2 3) '(4 5)) null map: all lists must have same size; arguments were: #<procedure:+> (1 2 3) (4 5) (cons (func (first list)) === context === /Applications/PLT/collects/scheme/private/misc.ss:7 (map1 func (rest list))))) 4:7 Define Lisp’s every and some Defining every is easy • every and some take a predicate and one or more sequences (define (every1 f list) • When given just one sequence, they test whether the elements satisfy the predicate ;; note the use of the and function > (every odd? ‘(1 3 5)) (if (null? list) #t > (some even? ‘(1 2 3)) #t #t • If given >1 sequences, the predicate takes as (and (f (first list)) many args as there are sequences and args (every1 f (rest list))))) are drawn one at a time from them: > (every > ‘(1 3 5) ‘(0 2 4)) #t Define some similarly Will this work? (define (some1 f list) • You can prove that P is true for some list ele- ment by showing that it isn’t false for every one (if (null? list) • Will this work? #f > (define (some1 f list) (or (f (first list)) (not (every1 (lambda (x) (not (f x))) list))) > (some1 odd? '(2 4 6 7 8)) (some1 f (rest list))))) #t > (some1 (lambda (x) (> x 10)) '(4 8 10 12)) #t 3 filter Example: filter (filter <f> <list>) returns a list of the elements of (define (filter1 func list) <list> which satisfy the predicate <f> ;; returns a list of elements of list where funct is true (cond ((null? list) null) > (filter odd? ‘(0 1 2 3 4 5)) ((func (first list)) (1 3 5) (cons (first list) (filter1 func (rest list)))) > (filter (lambda (x) (> x 98.6)) (#t (filter1 func (rest list))))) ‘(101.1 98.6 98.1 99.4 102.2)) (101.1 99.4 102.2) > (filter1 even? ‘(1 2 3 4 5 6 7)) (2 4 6) Example: filter Here’s another pattern • Define integers as a function that returns a list of integers between a min and max • We often want to do something like sum the (define (integers min max) elements of a sequence (if (> min max) (define (sum-list l) null (if (null? l) 0 (cons min (integers (add1 min) max)))) (+ (first l) (sum-list (rest l))))) • Do prime? as a predicate that is true of • Other times we want their product prime numbers and false otherwise (define (multiply-list l) > (filter prime? (integers 2 20) ) (if (null? l) (2 3 5 7 11 13 17 19) 1 (* (first l) (multiply-list (rest l))))) Here’s another pattern Example: reduce • We often want to do something like sum the • Reduce takes (i) a function, (ii) a final value elements of a sequence and (iii) a list of arguments (define (sum-list l) Reduce of +, 0, (v1 v2 v3 … vn) is just (if (null? l) 0 V1 + V2 + V3 + … Vn + 0 (+ (first l) (sum-list (rest l))))) • In Scheme/Lisp notation: • Other times we want their product > (reduce + 0 ‘(1 2 3 4 5)) (define (multiply-list l) 15 (if (null? l) 1 (reduce * 1 ‘(1 2 3 4 5)) (* (first l) (multiply-list (rest l))))) 120 4 Example: reduce (define (sum-list list) Using reduce ;; returns the sum of the list elements (define (reduce function final list) (reduce + 0 list)) (if (null? list) (define (mul-list list) ;; returns the sum of the list elements final (reduce * 1 list)) (function (define (copy-list list) (first list) ;; copies the top level of a list (reduce function final (rest list))))) (reduce cons ‘() list)) (define (append-list list) ;; appends all of the sublists in a list (reduce append ‘() list)) The roots of mapReduce Function composition • MapReduce is a software frame- • Math notation: gh is a composition of func- work developed by Google for tions g and h parallel computation on large datasets on computer clusters • If f=gh then f(x)=g(h(x) • It’s become an important way to • Composing functions is easy in Scheme exploit parallel computing using > compose > (define sd (compose sq conventional programming languages and techniques. #<procedure:compose> dub)) > (define (sq x) (* x x)) > (sd 10) • See Apache’s Hadoop for an > (define (dub x) (* x 2)) 400 open source version > (sq (dub 10)) > ((compose dub sq) 10) 400 200 • The framework was inspired by functional > (dub (sq 10)) programming’s map, reduce & side-effect free programs 200 Defining compose Functions with any number of args • Here’s compose for two functions in Scheme • Defining functions that takes any number of (define (compose2 f g) (lambda (x) (f (g x)))) arguments is easy in Scheme • Note that compose calls lambda which returns (define (foo . args) (printf "My args: ~a\n" a new function that applies f to the result of args))) applying g to x • If the parameter list ends in a symbol as • We’ll look at how the variable environments opposed to null (cf. dotted pair), then it’s value work to support this in the next topic, closures is the list of the remaining arguments’ values • But first, let’s see how to define a general ver- (define (f x y . more-args) …) sion of compose taking any number of args (define (map f . lists) … ) 5 Compose in Scheme A general every (define (compose . FS) ;; Returns the identity function if no args given • We can easily re-define other functions to take (if (null? FS) more than one argument (lambda (x) x) (define (every fn . args) (lambda (x) ((first FS) ((apply compose (rest FS)) x))))) (cond ((null? args) #f) ; examples ((null? (first args)) #t) (define (add-a-bang str) (string-append str "!")) ((apply fn (map first args)) (define givebang (compose string->symbol add-a-bang symbol->string)) (apply every fn (map rest args))) (givebang 'set) ; ===> set! (else #f))) ; anonymous composition • (every > ‘(1 2 3) ‘(0 2 3)) => #t ((compose sqrt negate square) 5) ; ===> 0+5i • (every > ‘(1 2 3) ‘(0 20 3)) => #f Functional Programming Summary • Lisp is the archetypal functional programming language • It treated functions as first-class objects and uses the same representation for data & code • The FP paradigm is a good match for many problems, esp.
Load more

Recommended publications
  • Functional Languages
    Functional Programming Languages (FPL) 1. Definitions................................................................... 2 2. Applications ................................................................ 2 3. Examples..................................................................... 3 4. FPL Characteristics:.................................................... 3 5. Lambda calculus (LC)................................................. 4 6. Functions in FPLs ....................................................... 7 7. Modern functional languages...................................... 9 8. Scheme overview...................................................... 11 8.1. Get your own Scheme from MIT...................... 11 8.2. General overview.............................................. 11 8.3. Data Typing ...................................................... 12 8.4. Comments ......................................................... 12 8.5. Recursion Instead of Iteration........................... 13 8.6. Evaluation ......................................................... 14 8.7. Storing and using Scheme code ........................ 14 8.8. Variables ........................................................... 15 8.9. Data types.......................................................... 16 8.10. Arithmetic functions ......................................... 17 8.11. Selection functions............................................ 18 8.12. Iteration............................................................. 23 8.13. Defining functions ...........................................
    [Show full text]
  • (Pdf) of from Push/Enter to Eval/Apply by Program Transformation
    From Push/Enter to Eval/Apply by Program Transformation MaciejPir´og JeremyGibbons Department of Computer Science University of Oxford [email protected] [email protected] Push/enter and eval/apply are two calling conventions used in implementations of functional lan- guages. In this paper, we explore the following observation: when considering functions with mul- tiple arguments, the stack under the push/enter and eval/apply conventions behaves similarly to two particular implementations of the list datatype: the regular cons-list and a form of lists with lazy concatenation respectively. Along the lines of Danvy et al.’s functional correspondence between def- initional interpreters and abstract machines, we use this observation to transform an abstract machine that implements push/enter into an abstract machine that implements eval/apply. We show that our method is flexible enough to transform the push/enter Spineless Tagless G-machine (which is the semantic core of the GHC Haskell compiler) into its eval/apply variant. 1 Introduction There are two standard calling conventions used to efficiently compile curried multi-argument functions in higher-order languages: push/enter (PE) and eval/apply (EA). With the PE convention, the caller pushes the arguments on the stack, and jumps to the function body. It is the responsibility of the function to find its arguments, when they are needed, on the stack. With the EA convention, the caller first evaluates the function to a normal form, from which it can read the number and kinds of arguments the function expects, and then it calls the function body with the right arguments.
    [Show full text]
  • Making a Faster Curry with Extensional Types
    Making a Faster Curry with Extensional Types Paul Downen Simon Peyton Jones Zachary Sullivan Microsoft Research Zena M. Ariola Cambridge, UK University of Oregon [email protected] Eugene, Oregon, USA [email protected] [email protected] [email protected] Abstract 1 Introduction Curried functions apparently take one argument at a time, Consider these two function definitions: which is slow. So optimizing compilers for higher-order lan- guages invariably have some mechanism for working around f1 = λx: let z = h x x in λy:e y z currying by passing several arguments at once, as many as f = λx:λy: let z = h x x in e y z the function can handle, which is known as its arity. But 2 such mechanisms are often ad-hoc, and do not work at all in higher-order functions. We show how extensional, call- It is highly desirable for an optimizing compiler to η ex- by-name functions have the correct behavior for directly pand f1 into f2. The function f1 takes only a single argu- expressing the arity of curried functions. And these exten- ment before returning a heap-allocated function closure; sional functions can stand side-by-side with functions native then that closure must subsequently be called by passing the to practical programming languages, which do not use call- second argument. In contrast, f2 can take both arguments by-name evaluation. Integrating call-by-name with other at once, without constructing an intermediate closure, and evaluation strategies in the same intermediate language ex- this can make a huge difference to run-time performance in presses the arity of a function in its type and gives a princi- practice [Marlow and Peyton Jones 2004].
    [Show full text]
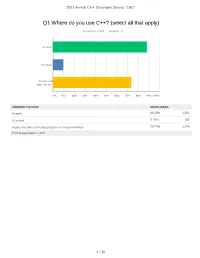
  • Q1 Where Do You Use C++? (Select All That Apply)
    2021 Annual C++ Developer Survey "Lite" Q1 Where do you use C++? (select all that apply) Answered: 1,870 Skipped: 3 At work At school In personal time, for ho... 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ANSWER CHOICES RESPONSES At work 88.29% 1,651 At school 9.79% 183 In personal time, for hobby projects or to try new things 73.74% 1,379 Total Respondents: 1,870 1 / 35 2021 Annual C++ Developer Survey "Lite" Q2 How many years of programming experience do you have in C++ specifically? Answered: 1,869 Skipped: 4 1-2 years 3-5 years 6-10 years 10-20 years >20 years 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ANSWER CHOICES RESPONSES 1-2 years 7.60% 142 3-5 years 20.60% 385 6-10 years 20.71% 387 10-20 years 30.02% 561 >20 years 21.08% 394 TOTAL 1,869 2 / 35 2021 Annual C++ Developer Survey "Lite" Q3 How many years of programming experience do you have overall (all languages)? Answered: 1,865 Skipped: 8 1-2 years 3-5 years 6-10 years 10-20 years >20 years 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% ANSWER CHOICES RESPONSES 1-2 years 1.02% 19 3-5 years 12.17% 227 6-10 years 22.68% 423 10-20 years 29.71% 554 >20 years 34.42% 642 TOTAL 1,865 3 / 35 2021 Annual C++ Developer Survey "Lite" Q4 What types of projects do you work on? (select all that apply) Answered: 1,861 Skipped: 12 Gaming (e.g., console and..
    [Show full text]
  • CSE 341 : Programming Languages
    CSE 341 : Programming Languages Lecture 10 Closure Idioms Zach Tatlock Spring 2014 More idioms • We know the rule for lexical scope and function closures – Now what is it good for A partial but wide-ranging list: • Pass functions with private data to iterators: Done • Combine functions (e.g., composition) • Currying (multi-arg functions and partial application) • Callbacks (e.g., in reactive programming) • Implementing an ADT with a record of functions (optional) 2 Combine functions Canonical example is function composition: fun compose (f,g) = fn x => f (g x) • Creates a closure that “remembers” what f and g are bound to • Type ('b -> 'c) * ('a -> 'b) -> ('a -> 'c) but the REPL prints something equivalent • ML standard library provides this as infix operator o • Example (third version best): fun sqrt_of_abs i = Math.sqrt(Real.fromInt(abs i)) fun sqrt_of_abs i = (Math.sqrt o Real.fromInt o abs) i val sqrt_of_abs = Math.sqrt o Real.fromInt o abs 3 Left-to-right or right-to-left val sqrt_of_abs = Math.sqrt o Real.fromInt o abs As in math, function composition is “right to left” – “take absolute value, convert to real, and take square root” – “square root of the conversion to real of absolute value” “Pipelines” of functions are common in functional programming and many programmers prefer left-to-right – Can define our own infix operator – This one is very popular (and predefined) in F# infix |> fun x |> f = f x fun sqrt_of_abs i = i |> abs |> Real.fromInt |> Math.sqrt 4 Another example • “Backup function” fun backup1 (f,g) = fn x => case
    [Show full text]
  • Specialising Dynamic Techniques for Implementing the Ruby Programming Language
    SPECIALISING DYNAMIC TECHNIQUES FOR IMPLEMENTING THE RUBY PROGRAMMING LANGUAGE A thesis submitted to the University of Manchester for the degree of Doctor of Philosophy in the Faculty of Engineering and Physical Sciences 2015 By Chris Seaton School of Computer Science This published copy of the thesis contains a couple of minor typographical corrections from the version deposited in the University of Manchester Library. [email protected] chrisseaton.com/phd 2 Contents List of Listings7 List of Tables9 List of Figures 11 Abstract 15 Declaration 17 Copyright 19 Acknowledgements 21 1 Introduction 23 1.1 Dynamic Programming Languages.................. 23 1.2 Idiomatic Ruby............................ 25 1.3 Research Questions.......................... 27 1.4 Implementation Work......................... 27 1.5 Contributions............................. 28 1.6 Publications.............................. 29 1.7 Thesis Structure............................ 31 2 Characteristics of Dynamic Languages 35 2.1 Ruby.................................. 35 2.2 Ruby on Rails............................. 36 2.3 Case Study: Idiomatic Ruby..................... 37 2.4 Summary............................... 49 3 3 Implementation of Dynamic Languages 51 3.1 Foundational Techniques....................... 51 3.2 Applied Techniques.......................... 59 3.3 Implementations of Ruby....................... 65 3.4 Parallelism and Concurrency..................... 72 3.5 Summary............................... 73 4 Evaluation Methodology 75 4.1 Evaluation Philosophy
    [Show full text]
  • Rootkits for Javascript Environments
    Rootkits for JavaScript Environments Ben Adida Adam Barth Collin Jackson Harvard University UC Berkeley Stanford University ben [email protected] [email protected] [email protected] Abstract Web Site Bookmarklet Web Site Bookmarklet A number of commercial cloud-based password managers use bookmarklets to automatically populate and submit login forms. Unfortunately, an attacker web Native JavaScript environment site can maliciously alter the JavaScript environment and, when the login bookmarklet is invoked, steal the Figure 1. Developers assume the bookmarklet in- user’s passwords. We describe general attack tech- teracts with the native JavaScript environment directly niques for altering a bookmarklet’s JavaScript envi- (left). In fact, the bookmarklet’s environment can be ronment and apply them to extracting passwords from manipulated by the current web page (right). six commercial password managers. Our proposed solution has been adopted by several of the commercial vendors. If the user clicks a bookmarklet while visiting an untrusted web page, the bookmarklet’s JavaScript is run in the context of the malicious page, potentially 1. Introduction letting an attacker manipulate its execution by care- fully crafting its JavaScript environment, essentially One promising direction for building engaging web installing a “rootkit” in its own JavaScript environment experiences is to combine content and functionality (See Figure 1). Instead of interacting with the native from multiple sources, often called a “mashup.” In JavaScript objects, the bookmarklet interacts with the a traditional mashup, an integrator combines gadgets attacker’s objects. This attack vector is not much of (such as advertisements [1], maps [2], or contact a concern for Delicious’ social bookmarking service, lists [3]), but an increasingly popular mashup design because the site’s own interests are served by advertis- involves the user adding a bookmarklet [4] (also known ing its true location and title.
    [Show full text]
  • Language Design and Implementation Using Ruby and the Interpreter Pattern
    Language Design and Implementation using Ruby and the Interpreter Pattern Ariel Ortiz Information Technology Department Tecnológico de Monterrey, Campus Estado de México Atizapán de Zaragoza, Estado de México, Mexico. 52926 [email protected] ABSTRACT to explore different language concepts and programming styles. In this paper, the S-expression Interpreter Framework (SIF) is Section 4 describes briefly how the SIF has been used in class. presented as a tool for teaching language design and The conclusions are found in section 5. implementation. The SIF is based on the interpreter design pattern and is written in the Ruby programming language. Its core is quite 1.1 S-Expressions S-expressions (symbolic expressions) are a parenthesized prefix small, but it can be easily extended by adding primitive notation, mainly used in the Lisp family languages. They were procedures and special forms. The SIF can be used to demonstrate selected as the framework’s source language notation because advanced language concepts (variable scopes, continuations, etc.) they offer important advantages: as well as different programming styles (functional, imperative, and object oriented). • Both code and data can be easily represented. Adding a new language construct is pretty straightforward. • Categories and Subject Descriptors The number of program elements is minimal, thus a parser is − relatively easy to write. D.3.4 [Programming Languages]: Processors interpreters, • run-time environments. The arity of operators doesn’t need to be fixed, so, for example, the + operator can be defined to accept any number of arguments. General Terms • There are no problems regarding operator precedence or Design, Languages. associativity, because every operator has its own pair of parentheses.
    [Show full text]
  • Locally Cartesian Closed Categories, Coalgebras, and Containers
    U.U.D.M. Project Report 2013:5 Locally cartesian closed categories, coalgebras, and containers Tilo Wiklund Examensarbete i matematik, 15 hp Handledare: Erik Palmgren, Stockholms universitet Examinator: Vera Koponen Mars 2013 Department of Mathematics Uppsala University Contents 1 Algebras and Coalgebras 1 1.1 Morphisms .................................... 2 1.2 Initial and terminal structures ........................... 4 1.3 Functoriality .................................... 6 1.4 (Co)recursion ................................... 7 1.5 Building final coalgebras ............................. 9 2 Bundles 13 2.1 Sums and products ................................ 14 2.2 Exponentials, fibre-wise ............................. 18 2.3 Bundles, fibre-wise ................................ 19 2.4 Lifting functors .................................. 21 2.5 A choice theorem ................................. 22 3 Enriching bundles 25 3.1 Enriched categories ................................ 26 3.2 Underlying categories ............................... 29 3.3 Enriched functors ................................. 31 3.4 Convenient strengths ............................... 33 3.5 Natural transformations .............................. 41 4 Containers 45 4.1 Container functors ................................ 45 4.2 Natural transformations .............................. 47 4.3 Strengths, revisited ................................ 50 4.4 Using shapes ................................... 53 4.5 Final remarks ................................... 56 i Introduction
    [Show full text]
  • Python and Roles of Variables in Introductory Programming: Experiences from Three Educational Institutions
    Journal of Information Technology Education Volume 6, 2007 Python and Roles of Variables in Introductory Programming: Experiences from Three Educational Institutions Uolevi Nikula Jorma Sajaniemi and Matti Tedre, Lappeenranta University of University of Joensuu, Finland Technology, Finland [email protected] [email protected] [email protected] Stuart Wray Royal School of Signals, Blandford, England [email protected] Executive Summary Students often find that learning to program is hard. Introductory programming courses have high drop-out rates and students do not learn to program well. This paper presents experiences from three educational institutions where introductory programming courses were improved by adopt- ing Python as the first programming language and roles of variables as an aid in understanding program behavior. As a result of these changes, students were able to write working code from the very beginning, they found programming easy and interesting, they passed exams with good grades, and drop-out rates were low. Students became interested in programming and some of them even changed their personal study plan to include more of programming and computer sci- ence. The high abstraction level and complexity of the concepts to be learned in current elementary programming courses is a serious impediment to students. Python is a simple but powerful pro- gramming language that supports both procedural and object-oriented programming. It makes short programs straightforward to write while at the same time facilitating rapid development of powerful applications. Python has been found to make programming more fun and thus attract students. Some of the common arguments against Python include concerns about using an inter- preted language, the different syntax from C++ and Java, the use of whitespace to represent code blocks, and the lack of static type checking.
    [Show full text]
  • 5Lesson 5: the Javascript Document Object Model (DOM)
    5Lesson 5: The JavaScript Document Object Model (DOM) Objectives By the end of the lesson, you will be able to: 2.2.1: Use JavaScript to manipulate the Document Object Model (DOM). 2.2.2: Use the window object of the DOM. 2.2.3: Manipulate properties and methods of the document object within the DOM. 2.2.4: Use the with statement. 2.2.5: Use the image object of the DOM, including image rollover creation. 2.2.6: Use the history object of the DOM. 2.2.7: Evaluate and change URL information with the location object of the DOM. 2.2.8: Use the navigator object of the DOM. 5-2 JavaScript Specialist Pre-Assessment Questions 1. The opener property of the window object refers to: a. a parent frame in a frameset. b. a parent window. c. the location of a window. d. a child window of another window. 2. The close() method of the document object: a. closes a document in a frame. b. closes all cookies associated with a document. c. closes a document in a window. d. closes the data stream to a document. 3. Discuss the difference between the name property and the src property of the image object. © 2011 Certification Partners, LLC. — All Rights Reserved. Version 1.01 Lesson 5: The JavaScript Document Object Model (DOM) 5-3 The JavaScript Document Object Model (DOM) OBJECTIVE JavaScript was designed explicitly for Web page use. To take advantage of the different 2.2.1: Manipulating features and capabilities provided by a browser, special browser objects have been built the DOM with JavaScript into the JavaScript language.
    [Show full text]
  • The Principles of Object-Oriented Javascript Zakas
    TAKETAKE CONTROLCONTROL OFOF Foreword by Cody Lindley, Best-selling Author and Principal Frontend Architect JAVASCRIPT THE PRINCIPLES OF OBJECT-ORIENTED JAVASCRIPT JAVASCRIPT THE PRINCIPLES OF OBJECT-ORIENTED JAVASCRIPT THETHE PRINCIPLESPRINCIPLES OFOF OBJECTSOBJECTS at TandemSeven OBJECT-ORIENTEDOBJECT-ORIENTED If you’ve used a more traditional object-oriented • How to define your own constructors JAVASCRIPTJAVASCRIPT language, such as C++ or Java, JavaScript probably • How to work with and understand prototypes doesn’t seem object-oriented at all. It has no concept of classes, and you don’t even need to define any • Inheritance patterns for types and objects objects in order to write code. But don’t be fooled — The Principles of Object-Oriented JavaScript will leave NICHOLAS C. ZAKAS JavaScript is an incredibly powerful and expressive even experienced developers with a deeper understand- object-oriented language that puts many design ing of JavaScript. Unlock the secrets behind how objects decisions right into your hands. work in JavaScript so you can write clearer, more In The Principles of Object-Oriented JavaScript, flexible, and more efficient code. Nicholas C. Zakas thoroughly explores JavaScript’s object-oriented nature, revealing the language’s A B O U T T H E A U T H O R unique implementation of inheritance and other key characteristics. You’ll learn: Nicholas C. Zakas is a software engineer at Box and is known for writing on and speaking about the latest • The difference between primitive and reference in JavaScript best practices. He honed his experience values during his five years at Yahoo!, where he was principal • What makes JavaScript functions so unique frontend engineer for the Yahoo! home page.
    [Show full text]