DOCSLIB.ORG

Surface Waves and Field Line Resonances: a THEMIS Case Study

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Surface Waves and Field Line Resonances: a THEMIS Case Study JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 114, A00C27, doi:10.1029/2008JA013553, 2009 Click Here for Full Article Surface waves and field line resonances: A THEMIS case study Oleksiy Agapitov,1 Karl-Heinz Glassmeier,2,3 Ferdinand Plaschke,2 Hans-Ulrich Auster,2 Dragos¸ Constantinescu,2 Vassilis Angelopoulos,4 Werner Magnes,5 Rumi Nakamura,5 Charles W. Carlson,6 Sabine Frey,6 and James P. McFadden6 Received 30 June 2008; revised 29 July 2009; accepted 6 August 2009; published 18 December 2009. [1] Using magnetic field and plasma observations from four of the five Time History of Events and Macroscale Interactions during Substorms (THEMIS) spacecraft, a surface wave at the dawn flank of the magnetopause was identified on 25 April 2007. The wave had an amplitude of about 1 RE and propagated tailward with a velocity of about 190–240 km/s. Its azimuthal wavelength was in the range of 9–11 RE. Magnetosheath velocity values support the hypothesis that this surface wave was generated by the Kelvin-Helmholtz instability. Simultaneously, an ultralow-frequency (ULF) pulsation event was detected by the fifth THEMIS spacecraft deeper in the magnetosphere, at a distance of about 5–7 RE from the magnetopause. This ULF event showed all the signatures predicted for waves generated by the classical field line resonance process. Frequency and phases of the detected ULF oscillations were found to be in close agreement with the magnetopause surface periodic disturbances. We conclude that the observed ULF wave event was most likely directly generated by the magnetopause surface wave and thus represents one of the few known manifestations of the classical field line resonance process in space directly observed, a conclusion made possible due to the special configuration of the THEMIS mission and its five spacecraft. Citation: Agapitov, O., et al. (2009), Surface waves and field line resonances: A THEMIS case study, J. Geophys. Res., 114, A00C27, doi:10.1029/2008JA013553. 1. Introduction decaying toward the inner magnetosphere, and its coupling to a localized Alfve´nic perturbation at a point where the local [2] Ultralow-frequency (ULF) pulsations in the period field line shell eigenfrequency equals the frequency of the range from 1 s to more then 600 s are one of the modes via driving surface wave. The typical characteristics of a global which the magnetosphere reacts to solar wind dynamics and FLR are predominantly toroidal magnetic field oscillations, associated instabilities of the magnetospheric system. One of localized in radial direction within the magnetosphere. the paradigms of ULF pulsation theory is the resonant Across the position of maximum field amplitude, the phase coupling of a compressional surface wave with toroidal of the toroidal component changes by 180° and the direction oscillations somewhere deeper in the magnetosphere. This of polarization is reversed [e.g., Nishida, 1978]. The spatially field line resonance (FLR) mechanism was first suggested by decaying surface mode is thought to be generated by the Tamao [1965] and later used by Southwood [1974] and Chen Kelvin-Helmholtz instability (KHI) of the dawn and dusk and Hasegawa [1974] to interpret observational results by magnetopause [e.g., Southwood, 1968; Pu and Kivelson, Samson et al. [1971]. A basic ingredient of the process is the 1983; Fujita et al., 1996], conditions for which are best when resonant interaction of a compressional mode, spatially passing through a high-speed solar wind stream [e.g., Seon et al., 1995; Engebretson et al., 1998]. A ULF pulsation 1Astronomy and Space Physics Department, National Taras generated by the described resonant coupling between a Shevchenko University of Kiev, Kiev, Ukraine. compressional surface wave and a toroidally polarized and 2Institut fu¨r Geophysik und extraterrestrische Physik, Technische spatially confined Alfvenic perturbation we define here as a Universita¨t Braunschweig, Braunschweig, Germany. classical field line resonance. 3Max-Planck-Institut fu¨r Sonnensystemforschung, Katlenburg-Lindau, Germany. [3] At the ground and in the ionosphere field line reso- 4Department of Earth and Space Sciences, University of California, nance associated oscillations are usually identified as lati- Los Angeles, California, USA. tudinally localized oscillations of the H component of the 5Space Research Institute, Austrian Academy of Sciences, Graz, magnetic field [e.g., Samson et al., 1971; Green, 1982; Austria. Glassmeier, 1988; Mathie et al., 1999a; Rae et al., 2005] or 6Space Sciences Laboratory, University of California, Berkeley, California, USA. in the NS component of the ionospheric electric field [e.g., Walker et al., 1979; Fenrich et al., 1995], associated with a Copyright 2009 by the American Geophysical Union. 180° phase shift across this resonantly oscillating field line 0148-0227/09/2008JA013553$09.00 A00C27 1of10 A00C27 AGAPITOV ET AL.: FIELD LINE RESONANCE A00C27 shell. In space, however, direct observations of field line bations, are discussed as an alternative to the KHI source resonances are very sparse. As direct observations we define mechanism [e.g., Kivelson and Southwood, 1985; Sinha and spatially and temporally resolved observations of wave- Rajaram, 2003]. Such perturbations can generate natural fields exhibiting typical spatial and temporal characteristics modes of the magnetospheric resonator with the polariza- of field line resonances. tion depending on the propagation direction and magnetic [4] Further possibilities to drive discrete frequency per- field disturbance vector [Agapitov and Cheremnykh, 2008]. turbations with frequencies in the ULF range are cavity and In their paper, these authors analyze periodic pulsations waveguide modes [e.g., Mann et al., 1999; Mills et al., associated with sudden impulse in spacecraft magnetic field 1999], sudden impulses of the solar wind [e.g., Saito and measurements and in ground based measurements at the Matsushita, 1967; Kivelson and Southwood, 1985], and magnetic conjugated point. Also, ULF pulsations with quasiperiodic changes of the solar wind dynamic pressure different frequencies were observed simultaneously on [e.g., Kepko and Spence, 2003]. different magnetic latitudes after a sudden impulse [e.g., [5] The waveguide theory predicts that the magneto- Glassmeier et al., 1984]. The existence of such spectral sphere can act as a cavity which traps discrete frequency maxima affirms the magnetospheric property of selecting compressional mode energy between the magnetosphere particular spectral peaks with global modes coupling to boundary and the reflection region inside the magneto- corresponding local field line shell oscillations. Qualitative sphere [e.g., Mann et al., 1999]. Most of the events confirmation of the experimental results were obtained analyzed by [e.g., Mathie et al., 1999b] using ground based extensive numerical modeling in a dipole magnetosphere observations can be explained in terms of such waveguide [e.g., Lysak and Lee, 1992]. modes and agree closely with the theory proposed by [9] Nevertheless, the many observations of FLRs at the Samson et al. [1992] and Mann et al. [1999], having ground and in the ionosphere on the one hand and the discrete frequencies of oscillation. CLUSTER measure- sparsity of space observations of classical field line reso- ments [Mann et al., 2002] furthermore support the hypoth- nances on the other hand is worthwhile to be noted. Here, esis that, during intervals of fast solar wind speed, the KHI we present observations from the five Time History of can excite magnetospheric waveguide modes which bathe Events and Macroscale Interactions during Substorms the flank magnetosphere with discrete frequency ULF wave (THEMIS) spacecraft [Angelopoulos, 2008], traversing the power and drive large amplitude resonant ULF pulsations. dusk magnetosphere on a highly elliptic orbit with the [6] Probably the best documented example of a KHI- spacecraft very often aligned in almost radial direction driven resonant ULF pulsation in space is the long-lasting during the coast phase of the mission. Such radial conjuga- event of 25 November 2001, reported about and analyzed in tions are ideal for studying surface waves and associated detail by Rae et al. [2005]. Multipoint observations from the field line resonances. We consider global ULF pulsations in CLUSTER and POLAR spacecraft allow one to demon- a study similar to Mann et al. [2002] and Rae et al. [2005] strate that KHI-driven surface waves drive resonant field with detail analysis of the magnetopause surface perturba- line oscillations. The data presented in this study provide tions. The simultaneous analysis of magnetopause pertur- evidence for an observational link between wave activity at bation and ULF waves inside the magnetosphere gave an the magnetopause, in the magnetosphere, and in the iono- opportunity to explain the properties of observed ULF sphere. The 25 November 2001 event certainly qualifies to waves and distinguish the different possible generation directly demonstrate the functionality of the classical field mechanisms. line resonance process. [7] Earlier studies by, e.g., Singer [1982] also reported 2. Observations radially localized, but poloidally polarized ULF waves using ISEE1 and ISEE2 observations and that allowed one to [10] THEMIS consists of five identically instrumented estimate the resonance region width to be about 0.7 RE. spacecraft, launched on 17 February 2007. The main goal Cramm et al. [2000] also reported such localized poloidal of this mission
Load more

Recommended publications
  • Localized Fast Flow Disturbance Observed in the Plasma Sheet And
    Annales Geophysicae (2005) 23: 553–566 SRef-ID: 1432-0576/ag/2005-23-553 Annales © European Geosciences Union 2005 Geophysicae Localized fast flow disturbance observed in the plasma sheet and in the ionosphere R. Nakamura1, O. Amm2, H. Laakso3, N. C. Draper4, M. Lester4, A. Grocott4, B. Klecker5, I. W. McCrea6, A. Balogh7, H. Reme` 8, and M. Andre´9 1Inst. fur¨ Weltraumforschung der Osterreichischen¨ Akademie der Wissenschaften, A-8042, Graz, Austria 2Finnish Meteorological Institute, Space Research, FIN-00101 Helsinki, Finland 3Solar and Solar Terrestrial Missions Div., ESTEC, 2200 AG Noordwijk, The Netherlands 4Radio and Space Plasma Physics Group, Dept. of Phys. and Astron., Leicester LE17RH, UK 5Max-Planck Inst. fur¨ Extraterrestrische Physik, D-85748 Garching, Germany 6Space Science and Technology Dept., Rutherford Appleton Lab., Chilton, Didcot, Oxon OX11QX, UK 7Space and Atmospheric Phys. Group, Blackett Lab., Imperial College, London SW72BZ, UK 8Centre d’Etude Spatiale des Rayonnements, F-31028 Toulouse Cedex 4, France 9Swedish Institute of Space Physics, SE-75121 Uppsala, Sweden Received: 22 June 2004 – Revised: 10 November 2004 – Accepted: 19 November 2004 – Published: 28 February 2005 Abstract. An isolated plasma sheet flow burst took Key words. Ionosphere (Electric fields and currents) – Mag- place at 22:02 UT, 1 September 2002, when the Clus- netosphere (Magnetosphere-ionosphere interactions; Plasma ter footpoint was located within the area covered by the convection) Magnetometers-Ionospheric Radars-All-sky Cameras Large Experiment (MIRACLE). The event was associated with a clear but weak ionospheric disturbance and took place during 1 Introduction a steady southward IMF interval, about 1 h preceding a ma- jor substorm onset.
    [Show full text]
  • Cluster 5 Years
    1 TAIL RECONNECTION AND PLASMA SHEET FAST FLOWS Rumi Nakamura, Wolfgang Baumjohann, Andrei Runov, and Yoshihiro Asano Space Research Institute, Austrian Academy of Sciences, Schmiedlstr. 6, A–8042 Graz, Austria, Email: [email protected] ABSTRACT and energy transport in the magnetotail. These fast flows are considered to take place as a consequence of recon- nection. The flows near the boundary of the plasma sheet The present state of understanding the process of tail re- consist of field-aligned beams, whereas the flows in the connection and plasma sheet fast flows obtained from central plasma sheet tend to have a large bulk-flow com- Cluster measurements is reviewed. Being a constellation ponent. The latter flows organize themselves in 10-min of four identical spacecraft, Cluster allows discrimination timescale flow enhancements, which are called bursty of spatial and temporal variations in magnetic field and bulk flow (BBF) events, embedding velocity peaks of 1- plasma parameters. Thus it is ideal to study the structure min duration, which are called flow bursts, and have char- and dynamics of plasma and fields relevant to reconnec- acteristics distinctly different from plasma sheet bound- tion, which is a highly dynamic system. Observations of ary layer flows (1; 2). current sheet crossings near the X-line obtained the ge- ometry of reconnection region and confirmed the effects Cluster traversed the magnetotail covering regions Earth- of unmagnetized ions including the Hall-current and its ward of 19 RE during the past four summer seasons since closure currents. Cluster multi-point observations iden- July 2001. The tetrahedron scale was between 250 km tified three dimensional structures and dynamics of the and 4000 km, which were changed every year, so that fast flows in the plasma sheet, which could be ascribed to characteristics at different scales could be identified.
    [Show full text]
  • Evolution of Dipolarization in the Near-Earth Current Sheet Induced by Earthward Rapid flux Transport
    Ann. Geophys., 27, 1743–1754, 2009 www.ann-geophys.net/27/1743/2009/ Annales © Author(s) 2009. This work is distributed under Geophysicae the Creative Commons Attribution 3.0 License. Evolution of dipolarization in the near-Earth current sheet induced by Earthward rapid flux transport R. Nakamura1, A. Retino`1, W. Baumjohann1, M. Volwerk1, N. Erkaev2, B. Klecker3, E. A. Lucek4, I. Dandouras5, M. Andre´6, and Y. Khotyaintsev6 1Space Research Institute, Austrian Academy of Sciences, 8042 Graz, Austria 2Institute of Computation Modelling, Russian Academy of Sciences, Siberian Branch, Krasnoyarsk, Russia 3Max-Planck-Institut fur¨ extraterrestrische Physik, P.O. Box 1312, Garching, 85741, Germany 4Imperial College, London, SW7 2BZ, UK 5CESR/CNRS, 9 Ave. du Colonel Roche, B.P. 4346, 31028 Toulouse Cedex 4, France 6Swedish Institute of Space Physics, P.O. Box 537, 75121 Uppsala, Sweden Received: 6 October 2008 – Revised: 5 February 2009 – Accepted: 18 February 2009 – Published: 9 April 2009 Abstract. We report on the evolution of dipolarization dipolarization pulses could differ, depending on the configu- and associated disturbances of the near-Earth current sheet ration of the current sheet. during a substorm on 27 October 2007, based upon Clus- Keywords. Magnetospheric physics (Plasma convection; ter multi-point, multi-scale observations of the night-side Plasma sheet; Storms and substorms) plasma sheet at X∼−10 RE. Three dipolarization events were observed accompanied by activations on ground mag- netograms at 09:07, 09:14, and 09:22 UT. We
    [Show full text]
  • A Space Plasma Physics Data Resource for the ESA Cluster Active Archive
    1 ECLAT European Cluster Assimilation Technology A space plasma physics data resource for the ESA Cluster Active Archive 2 Contents 1. Scientific and technical description 3 1.1 Concepts and objectives 3 1.1.1 Micro-scale, in situ fundamental plasma physics 5 1.1.2 Meso-scale ionospheric observations for coordinated space- and ground-based studies of magnetosphere-ionosphere coupling 6 1.1.3 Global scale observations for system-level studies of magnetospheric dynamics and solar wind-magnetosphere-ionosphere coupling 8 1.1.4 Physics-based modelling of the magnetosphere 9 1.1.5 Assimilation and “reanalysis” of observation data and model simulation 10 1.2 Progress beyond the state-of-the-art 11 1.2.1 Present state-of-the-art 11 1.2.2 Anticipated achievements of ECLAT 13 1.3 Methodology and work plan 14 1.3.1 Overall strategy of the work plan 14 1.3.2 Detailed work package descriptions 16 1.4 References 18 2. Implementation 20 2.1 Management structure 20 2.1.1 Executive board, management support team, advisory panel, and work-package leaders 20 2.1.3 Project meetings and workshops 21 2.2 Individual participants 22 2.2.1 University of Leicester, UK 22 2.2.2 Oesterreichische Akademie der Wissenschaften, Austria 23 2.2.3 Finnish Meteorological Institute, Finland 24 2.2.4 St. Petersburg State University, Russia 25 2.2.5 Institutet för rymdfysik, Sweden 27 3. Impact 28 3.1 Expected impacts listed in the work programme 28 3 European Cluster Assimilation Technology (ECLAT) Principle proponents: Steve MILAN, Mark LESTER (ULEIC, UK); Rumi NAKAMURA (OEAW, Austria); Kirsti KAURISTIE, Minna PALMROTH (FMI, Finland); Victor SERGEEV (SPSU, Russia); and Hermann OPGENOORTH (IRF, Sweden).
    [Show full text]
  • ECLAT D600.1 Report and “Lessons Learned” from the 1St ECLAT Scientific Workshop October 22 – 24, FMI, Helsinki, Finland Hermann Opgenoorth, IRF
    ECLAT D600.1 ECLAT D600.1 Report and “Lessons Learned” from the 1st ECLAT Scientific Workshop October 22 – 24, FMI, Helsinki, Finland Hermann Opgenoorth, IRF The workshop was the first in a sequence of four topically organised ECLAT workshops and it was dedicated to initiate the scientific quality control of the delivered ECLAT data products, in particular the reliability of Cluster footprint mapping using various models during various level of magnetospheric activities, including substorms and localised field aligned currents. The workshop was attended by 30 persons, stemming mainly from the teams of the participating ECLAT partners, CAA and ESA staff, and members of the ECLAT Advisory Board. The program/agenda of the workshop can be found in a separate appendix. All presentations during the workshop have been placed in a dedicated workshop folder on the Internet. In the following we will summarise the discussions under the various agenda items and point out “Lessons Learned” and decisions for “Action Items” for the next ECLAT workshop. Workshop Introductory Talks Steve Milan opened the workshop with a general introduction to the ECLAT project. Rumi Nakamura and Pete Boakes gave a status update on the OEAW region identification product and event finding activities. • The defined and characterised regions are: Lobe, boundary region, outer plasma sheet, inner plasma sheet, the neutral sheet and the plasma sheet boundary layer. • In addition to the identification of such boundaries there will be event lists addressing in particular dynamic features like wavy current sheet, depolarization events and occurrences of thin current sheets and large FACs. • In the following discussion the issue of a difference between OPS (being a region dominated by currents) and PSBL (being dominated by flows) was raised and discussed.
    [Show full text]
  • Lowaltitude Electron Acceleration Due to Multiple Flow Bursts in The
    GeophysicalResearchLetters RESEARCH LETTER Low-altitude electron acceleration due to multiple flow 10.1002/2013GL058982 bursts in the magnetotail Key Points: R. Nakamura1, T. Karlsson2, M. Hamrin3, H. Nilsson4, O. Marghitu5,O.Amm6, C. Bunescu5, • First observation of multiple flow V. Constantinescu5,H.U.Frey7, A. Keiling7, J. Semeter8, E. Sorbalo9,J.Vogt9, signatures on near-conjugate 10 11 flux tubes C. Forsyth , and M. V. Kubyshkina • Low-energy electron profile suggests Alfvénic acceleration due to fast flow 1Space Research Institute, Austrian Academy of Sciences, Graz, Austria, 2Space and Plasma Physics, Royal Institute of • Multiple flow bursts are obtained Technology, Stockholm, Sweden, 3Department of Physics, Umeå University, Umeå, Sweden, 4Swedish Institute of Space to extend over large radial distance Physics, Kiruna, Sweden, 5Institute for Space Sciences, Bucharest, Romania, 6Finnish Meteorological Institute, Helsinki, in tail Finland, 7Space Sciences, Laboratory, University of California, Berkeley, California, USA, 8Department of Electrical and Computer Engineering, Boston University, Boston, Massachusetts, USA, 9School of Engineering and Science, Jacobs Supporting Information: University Bremen, Bremen, Germany, 10UCL Mullard Space Science Laboratory, Dorking, UK, 11Earth Physics • Readme Department, St. Petersburg State University, St. Petersburg, Russia • Figure S1 • Figure S2 Abstract At 10:00 UT on 25 February 2008, Cluster 1 spacecraft crossed the near-midnight auroral zone, Correspondence to: at about 2 RE altitude, while two of the Time History of Events and Macroscale Interactions During R. Nakamura, Substorms (THEMIS) spacecraft, THD and THE, observed multiple flow bursts on the near-conjugate [email protected] plasma sheet field lines. The flow shear pattern at THEMIS was consistent with the vortical motion at duskside of a localized flow channel.
    [Show full text]
  • Near-Earth Plasma Sheet Boundary Dynamics During Substorm
    Nakamura et al. Earth, Planets and Space (2017) 69:129 DOI 10.1186/s40623-017-0707-2 FRONTIER LETTER Open Access Near‑Earth plasma sheet boundary dynamics during substorm dipolarization Rumi Nakamura1* , Tsugunobu Nagai2, Joachim Birn3, Victor A. Sergeev4, Olivier Le Contel5, Ali Varsani1, Wolfgang Baumjohann1, Takuma Nakamura1, Sergey Apatenkov4, Anton Artemyev6, Robert E. Ergun7, Stephen A. Fuselier8, Daniel J. Gershman9, Barbara J. Giles9, Yuri V. Khotyaintsev10, Per‑Arne Lindqvist11, Werner Magnes1, Barry Mauk12, Christopher T. Russell6, Howard J. Singer13, Julia Stawarz14, Robert J. Strangeway6, Brian Anderson12, Ken R. Bromund9, David Fischer1, Laurence Kepko9, Guan Le9, Ferdinand Plaschke1, James A. Slavin15, Ian Cohen12, Allison Jaynes7 and Drew L. Turner16 Abstract We report on the large-scale evolution of dipolarization in the near-Earth plasma sheet during an intense (AL ~ 1000 nT) substorm on August 10, 2016, when multiple spacecraft at radial distances between 4 and 15 RE were present− in the night-side magnetosphere. This global dipolarization consisted of multiple short-timescale (a couple of minutes) Bz disturbances detected by spacecraft distributed over 9 MLT, consistent with the large-scale substorm current wedge observed by ground-based magnetometers. The four spacecraft of the Magnetospheric Mul‑ tiscale were located in the southern hemisphere plasma sheet and observed fast fow disturbances associated with this dipolarization. The high-time-resolution measurements from MMS enable us to detect the rapid motion of the feld structures and fow disturbances separately. A distinct pattern of the fow and feld disturbance near the plasma boundaries was found. We suggest that a vortex motion created around the localized fows resulted in another feld- aligned current system at the of-equatorial side of the BBF-associated R1/R2 systems, as was predicted by the MHD simulation of a localized reconnection jet.
    [Show full text]
  • Space Plasma Introduction Rumi Nakamura
    INSTITUT FÜR WELTRAUMFORSCHUNG VOYAGE 2050 WORKSHOP, OCTOBER 29-31 2019, MADRID The Sun, planets, magnetosphere and plasma physics: Space Plasma Introduction Rumi Nakamura Space Research Institute, Austrian Academy of Sciences IWF.OEAW.AC.AT (Moore, Burch et al., 2017) INSTITUT FÜR WELTRAUMFORSCHUNG IN-SITU PLASMA MEASUREMENTS Earth magnetosphere Heliosphere IWF.OEAW.AC.AT INSTITUT FÜR WELTRAUMFORSCHUNG Space Plasma White Papers Solar & “Heliospheric” plasma • S. Matthews: Solar Particle Acceleration, Radiation & Kinetics • I. McCrea:"The Grand European Heliospheric Observatory" • R. Wimmer-Schweingruber: In-situ Investigations of the Local Interstellar Medium Near Earth plasma • J. Rae: What are the fundamental modes of energy transfer and partitioning in the coupled Magnetosphere-Ionosphere system? • A. Retino: Particle Energization in Space Plasmas: Towards a Multi-Point, Multi-Scale Plasma Observatory • D. Verscharen/R. Wicks: A Case for Electron-Astrophysics • G. Branduardi-Raymont: Exploring Solar-Terrestrial Interactions via Multiple Observers Planetary plasma • E. Roussos: The in-situ exploration of Jupiter's radiation belts • B. Sanchez-Cano: Mars' plasma system, Scientific potential of coordinated multi-point missions, 'The next generation‘ • M. Yamauchi: Plasma-neutral gas interactions in various space environments IWF.OEAW.AC.AT INSTITUT FÜR WELTRAUMFORSCHUNG White papers with also interest in space plasma Solar plasma • V. Krasnoselskikh: In situ studies of the solar corona after Parker Solar Probe and Solar Orbiter Planets & Moons • L. Fletcher: Ice Giant Systems: Scientific Potential of Missions to Uranus and Neptune • A. Sulaiman: Enceladus and Titan: Emerging worlds of the solar system • G. Choblet: Enceladus as a potential oasis for life: Science goals and investigations for future explorations • S. Rodriguez: Science goals and mission concepts for a future orbital and in situ exploration of Titan • M.
    [Show full text]
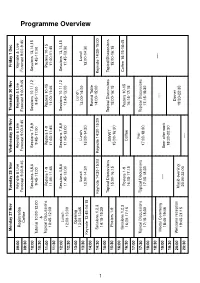
  • Program Booklet (Pdf)
    Monday 27 Nov Tuesday 28 Nov Wednesday 29 Nov Thursday 30 Nov Friday 1 Dec 09:00 Keynote & Live Keynote & Live Keynote & Live Keynote & Live Registration Programme Overview Forecast 9:00-9:45 Forecast 9:00-9:45 Forecast 9:00-9:45 Forecast 9:00-9:45 09:30 Coffee 10:00 Sessions 4,5,6 Sessions 7,8,9 Sessions 10,11,12 Sessions 13,14,15 Tutorial 10:00-12:00 9:45-11:00 9:45-11:00 9:45-11:00 9:45-11:00 10:30 & 11:00 Topical Discussions Posters 1-9 Posters 1-9 Posters 10-15 Posters 10-15 10:45-12:00 11:00-11:45 11:00-11:45 11:00-11:45 11:00-11:45 11:30 12:00 Lunch Sessions 4,5,6 Sessions 7,8,9 Sessions 10,11,12 Sessions 13,14,15 11:45-13:00 11:45-13:00 11:45-13:00 11:45-13:00 12:30 12:00-13:00 13:00 Opening Lunch 13:00-13:45 Lunch Lunch Lunch 13:30 13:00-14:00 Keynote 13:45-14:15 13:00-14:30 13:00-14:30 13:00-14:30 14:00 Round Table Sessions 1,2,3 14:00-15:00 1 14:30 Keynote 14:30-15:00 Keynote 14:30-15:00 Keynote 14:30-15:00 14:15-15:30 15:00 Topical Discussions SWWT Topical Discussions Topical Discussions 15:30 Posters 1-9 15:00-16:15 15:00-16:30 15:00-16:15 15:00-16:15 16:00 Sessions 1,2,3 Posters 1-9 Posters 10-15 Coffee 16:15-16:45 16:30 Coffee 16:00-17:15 16:15-17:15 16:15-17:15 17:00 Fair 17:30 Topical Discussions Topical Discussions Topical Discussions 17:15-18:30 17:15-18:30 17:00-18:30 17:15-18:30 18:00 —- 18:30 —- Medal Ceremony —- 19:00 —- 18:45-19:45 Beer after work 19:30 18:30-20:30 Dinner 20:00 Welcome reception Music evening 19:45-21:15 19:30-22:30 20:30 20:00-22:00 —- Floor Plan 2 Monday, 27 November 2017 09:00 Registration desk
    [Show full text]
  • On the Basis of All-Sky TV Records of Auroras, Faint Auroral
    J. Geomag. Geoelectr., 39, 609-624,1987 Oscillations in Drifts of Auroral Patches Takasi OGUTI,Rumi NAKAMURA,and Tatsundo YAMAMOTO GeophysicsResearch Laboratory, Universityof Tokyo, Tokyo, Japan (ReceivedJune 11,1987; Revised August 3, 1987) On the basis of all-sky TV records of auroras, faint auroral patches (non- pulsating in luminosity) are found to oscillatorily drift associated with concurrent magneticpulsations on the ground. These oscillationsin the drifts of auroral patches are found to be consistent with the oscillations in the electrostatic electric field associatedwith the concurrent magneticpulsations. This impliesthat these magnetic pulsations are brought forth by ionospheric electric currents which are produced by electrostaticelectric fieldsassociated with shear Alfven waves in the magnetosphere. The result, therefore, indicates that the simultaneous measurement of the drifts of auroral structures at the time of ground magneticpulsations is a convenient method of examining whether the magneticpulsations are really ascribedto HM wavefields propagating down from the magnetosphere,or if they are essentiallycaused by the change in conductivity inhomogeneity in the ionosphere. It is also shown that the azimuthal phase speed (wave length), as well as the oscillation amplitude, highly varies from the dayside to the evening, i.e., it is larger in the dayside and becomes much smaller toward the evening sectors. Theory must take this steep longitudinal non-uniformityinto consideration. 1. Introduction Faint auroral patches (non-pulsating in luminosity) were seen above La Ronge, Saskatchewan, Canada, in the evening on February 17, 1980 during the period of the joint University of Tokyo-University of British Columbia Aurora-ULF-VLF campaign, coordinated with the Canadian Pulsating Aurora Campaign (MCEWEN and DUNCAN,1981).
    [Show full text]
  • A Debate on Substorm Expansion Onset Mechanism
    Updating the Near-Earth Neutral Line Model Wolfgang Baumjohann & Rumi Nakamura Institut für Weltraumphysik der Österreichischen Akademie der Wissenschaften Schmiedlstrasse 6, A-8042 Graz, Austria Email: [email protected], [email protected] Abstract In the past thirty years the Near-Earth Neutral Line model for substorms has been proven to be correct in its ba- sic assumption, i.e., that a new neutral line is created near the Earth during substorm onset. Yet there have also been numerous changes and additions to this model, which were necessary to give a more complete and deeper understanding of the substorm process. This process is still continuing. 1. Introduction More than three decades ago, the first phenomenological description of substorm in terms of auroral activity was introduced (Akasofu, 1964). The auroral substorm concept was extended soon after to encompass disturbances throughout the entire magnetosphere-ionosphere system. The energy for substorms was attributed to a physical process known as magnetic reconnection, envisioned to convert energy between magnetic field and charged particles by cutting magnetic field lines and rejoining them with different ones. Thirty years ago, McPherron et al. (1970) and Hones et al. (1970) have put together the first aspects of a phe- nomenological substorm model, which had as key ingredient the development of a new magnetic neutral line closer to the Earth (than the distant neutral line at about 80-100 RE) during substorm onset, and was subsequently called Near-Earth Neutral Line model, or short NENL model. This model has now been around for more than 25 years. During these years, it has been evolved considerably.
    [Show full text]
  • Plasma Coupling in the Auroral Magnetosphere–Ionosphere System (POLARIS)
    Proposal for an ISSI International Team in Space Science Plasma Coupling in the Auroral Magnetosphere–Ionosphere System (POLARIS) Abstract Astrophysical context. Fundamental processes in the plasma universe are often organized by magnetic fields and accompanied by energetic particles. Examples range from planetary aurorae and solar activity to astrophysical shocks and pulsar magnetospheres (Fig. 1). Magnetic coupling works across very different plasma regimes and may yield complex interaction patterns. An ideal test-bed for studying this type of fundamental plasma coupling is the geospace environment where the collisionless magnetospheric plasma interacts with the collisional polar ionosphere through exchange of energetic particles, electromagnetic fields and currents. While the magnetosphere–ionosphere (M–I) coupling in the morning and evening sectors is often rather steady and can be well described by simplified current systems and electromagnetic fields, the transition region in the midnight sector (Fig. 2), known as the Harang region (HR), is much more dynamic. The current and field configuration is complex and essentially three-dimensional, and the HR is believed to play an important role in the substorm cycle. The auroral M–I system is typically far from equilibrium and the substorm phases correspond to different conditions of the large scale energy flux through this system, associated with loading / unloading of magnetic energy. Even if a direct connection is difficult to establish at present, similar systems may occur quite generally in magnetized astrophysical plasmas. Project objectives. The project aims to investigate the M–I coupling modes in the HR, by exploring the 3-D configuration and temporal evolution of the system during the various substorm phases.
    [Show full text]