DOCSLIB.ORG

Module 1 Atomic and Nuclear Physics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Module 1 Atomic and Nuclear Physics DOE Fundamentals NUCLEAR PHYSICS AND REACTOR THEORY Module 1 Atomic and Nuclear Physics NUCLEAR PHYSICS AND REACTOR THEORY TABLE OF CONTENTS C TABLE OF CONTENTS ................................................................................................ i LIST OF FIGURES ......................................................................................................iv LIST OF TABLES ......................................................................................................... v REFERENCES ............................................................................................................vi OBJECTIVES .............................................................................................................. vii ATOMIC NATURE OF MATTER .................................................................................. 1 Structure of Matter .................................................................................................... 1 Subatomic Particles .................................................................................................. 2 Bohr Model of the Atom ............................................................................................ 2 Measuring Units on the Atomic Scale ....................................................................... 4 Nuclides .................................................................................................................... 4 Isotopes .................................................................................................................... 5 Atomic and Nuclear Radii ......................................................................................... 6 Nuclear Forces ......................................................................................................... 7 Summary .................................................................................................................. 9 CHART OF THE NUCLIDES ..................................................................................... 11 Chart of the Nuclides .............................................................................................. 11 Information for Stable Nuclides ............................................................................... 12 Neutron - Proton Ratios .......................................................................................... 13 Natural Abundance of Isotopes............................................................................... 14 Enriched and Depleted Uranium ............................................................................. 15 Summary ................................................................................................................ 15 MASS DEFECT AND BINDING ENERGY ................................................................. 17 Mass Defect ............................................................................................................ 17 Binding Energy ....................................................................................................... 18 Energy Levels of Atoms .......................................................................................... 19 Energy Levels of the Nucleus ................................................................................. 20 Summary ................................................................................................................ 21 MODES OF RADIOACTIVE DECAY ......................................................................... 22 Stability of Nuclei .................................................................................................... 22 Natural Radioactivity ............................................................................................... 22 Nuclear Decay ........................................................................................................ 23 I-i NUCLEAR PHYSICS AND REACTOR THEORY Alpha Decay (a) ...................................................................................................... 23 Beta Decay (ẞ) ....................................................................................................... 24 Electron Capture (EC, K-capture) ........................................................................... 24 Gamma Emission (Ɣ) .............................................................................................. 25 Internal Conversion................................................................................................. 26 Decay Chains ......................................................................................................... 26 Predicting Type of Decay ........................................................................................ 27 Summary ................................................................................................................ 29 RADIOACTIVITY ....................................................................................................... 30 Radioactive Decay Rates ....................................................................................... 30 Units of Measurement for Radioactivity .................................................................. 31 Variation of Radioactivity Over Time ....................................................................... 31 Radioactive Half-Life ............................................................................................... 32 Plotting Radioactive Decay ..................................................................................... 35 Radioactive Equilibrium .......................................................................................... 37 Transient Radioactive Equilibrium .......................................................................... 40 Summary ................................................................................................................ 41 NEUTRON INTERACTIONS ...................................................................................... 43 Scattering ............................................................................................................... 43 Elastic Scattering .................................................................................................... 43 Inelastic Scattering ................................................................................................. 45 Absorption Reactions .............................................................................................. 45 Radiative Capture ................................................................................................... 46 Particle Ejection ...................................................................................................... 46 Fission .................................................................................................................... 46 NUCLEAR FISSION .................................................................................................. 48 Fission .................................................................................................................... 48 Liquid Drop Model of a Nucleus .............................................................................. 48 Critical Energy ........................................................................................................ 50 Fissile Material ........................................................................................................ 50 Fissionable Material ................................................................................................ 50 Fertile Material ........................................................................................................ 51 Binding Energy Per Nucleon (BE/A) ....................................................................... 52 ENERGY RELEASE FROM FISSION ....................................................................... 56 I-ii NUCLEAR PHYSICS AND REACTOR THEORY Calculation of Fission Energy ................................................................................. 56 Estimation of Decay Energy ................................................................................... 60 Distribution of Fission Energy ................................................................................. 61 INTERACTION OF RADIATION WITH MATTER ...................................................... 63 Interaction of Radiation With Matter........................................................................ 63 Alpha Radiation ...................................................................................................... 64 Beta-Minus Radiation ............................................................................................. 64 Positron Radiation .................................................................................................. 65 Neutron Radiation ................................................................................................... 65 Gamma Radiation ................................................................................................... 66 Summary ................................................................................................................ 67 I-iii NUCLEAR PHYSICS AND REACTOR THEORY LIST OF FIGURES Figure 1 Bohr's Model of the Hydrogen Atom ................................................................ 3 Figure 2 Nomenclature for Identifying Nuclides ............................................................
Load more

Recommended publications
  • Chapter 4. CLASSIFICATION UNDER the ATOMIC ENERGY
    Chapter 4 CLASSIFICATION UNDER THE ATOMIC ENERGY ACT INTRODUCTION The Atomic Energy Act of 1946 was the first and, other than its successor, the Atomic Energy Act of 1954, to date the only U.S. statute to establish a program to restrict the dissemination of information. This Act transferred control of all aspects of atomic (nuclear) energy from the Army, which had managed the government’s World War II Manhattan Project to produce atomic bombs, to a five-member civilian Atomic Energy Commission (AEC). These new types of bombs, of awesome power, had been developed under stringent secrecy and security conditions. Congress, in enacting the 1946 Atomic Energy Act, continued the Manhattan Project’s comprehensive, rigid controls on U.S. information about atomic bombs and other aspects of atomic energy. That Atomic Energy Act designated the atomic energy information to be protected as “Restricted Data” and defined that data. Two types of atomic energy information were defined by the Atomic Energy Act of 1954, Restricted Data (RD) and a type that was subsequently termed Formerly Restricted Data (FRD). Before discussing further the Atomic Energy Act of 1946 and its unique requirements for controlling atomic energy information, some of the special information-control activities that accompanied the research, development, and production efforts that led to the first atomic bomb will be mentioned. Realization that an atomic bomb was possible had a profound impact on the scientists who first became aware of that possibility. The implications of such a weapon were so tremendous that the U.S. scientists conducting the initial, basic research related to nuclear fission voluntarily restricted the publication of their scientific work in this area.
    [Show full text]
  • B2.IV Nuclear and Particle Physics
    B2.IV Nuclear and Particle Physics A.J. Barr February 13, 2014 ii Contents 1 Introduction 1 2 Nuclear 3 2.1 Structure of matter and energy scales . 3 2.2 Binding Energy . 4 2.2.1 Semi-empirical mass formula . 4 2.3 Decays and reactions . 8 2.3.1 Alpha Decays . 10 2.3.2 Beta decays . 13 2.4 Nuclear Scattering . 18 2.4.1 Cross sections . 18 2.4.2 Resonances and the Breit-Wigner formula . 19 2.4.3 Nuclear scattering and form factors . 22 2.5 Key points . 24 Appendices 25 2.A Natural units . 25 2.B Tools . 26 2.B.1 Decays and the Fermi Golden Rule . 26 2.B.2 Density of states . 26 2.B.3 Fermi G.R. example . 27 2.B.4 Lifetimes and decays . 27 2.B.5 The flux factor . 28 2.B.6 Luminosity . 28 2.C Shell Model § ............................. 29 2.D Gamma decays § ............................ 29 3 Hadrons 33 3.1 Introduction . 33 3.1.1 Pions . 33 3.1.2 Baryon number conservation . 34 3.1.3 Delta baryons . 35 3.2 Linear Accelerators . 36 iii CONTENTS CONTENTS 3.3 Symmetries . 36 3.3.1 Baryons . 37 3.3.2 Mesons . 37 3.3.3 Quark flow diagrams . 38 3.3.4 Strangeness . 39 3.3.5 Pseudoscalar octet . 40 3.3.6 Baryon octet . 40 3.4 Colour . 41 3.5 Heavier quarks . 43 3.6 Charmonium . 45 3.7 Hadron decays . 47 Appendices 48 3.A Isospin § ................................ 49 3.B Discovery of the Omega § ......................
    [Show full text]
  • Pair Energy of Proton and Neutron in Atomic Nuclei
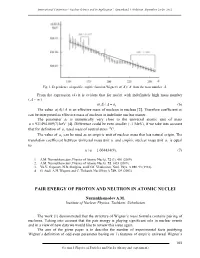
    International Conference “Nuclear Science and its Application”, Samarkand, Uzbekistan, September 25-28, 2012 Fig. 1. Dependence of specific empiric function Wigner's a()/ A A from the mass number A. From the expression (4) it is evident that for nuclei with indefinitely high mass number ( A ~ ) a()/. A A a1 (6) The value a()/ A A is an effective mass of nucleon in nucleus [2]. Therefore coefficient a1 can be interpreted as effective mass of nucleon in indefinite nuclear matter. The parameter a1 is numerically very close to the universal atomic unit of mass u 931494.009(7) keV [4]. Difference could be even smaller (~1 MeV), if we take into account that for definition of u, used mass of neutral atom 12C. The value of a1 can be used as an empiric unit of nuclear mass that has natural origin. The translation coefficient between universal mass unit u and empiric nuclear mass unit a1 is equal to: u/ a1 1.004434(9). (7) 1. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72 (3), 401 (2009). 2. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72, 1435 (2009). 3. Yu.V. Gaponov, N.B. Shulgina, and D.M. Vladimirov, Nucl. Phys. A 391, 93 (1982). 4. G. Audi, A.H. Wapstra and C. Thibault, Nucl.Phys A 729, 129 (2003). PAIR ENERGY OF PROTON AND NEUTRON IN ATOMIC NUCLEI Nurmukhamedov A.M. Institute of Nuclear Physics, Tashkent, Uzbekistan The work [1] demonstrated that the structure of Wigner’s mass formula contains pairing of nucleons. Taking into account that the pair energy is playing significant role in nuclear events and in a view of new data we would like to review this issue again.
    [Show full text]
  • Compilation and Evaluation of Fission Yield Nuclear Data Iaea, Vienna, 2000 Iaea-Tecdoc-1168 Issn 1011–4289
    IAEA-TECDOC-1168 Compilation and evaluation of fission yield nuclear data Final report of a co-ordinated research project 1991–1996 December 2000 The originating Section of this publication in the IAEA was: Nuclear Data Section International Atomic Energy Agency Wagramer Strasse 5 P.O. Box 100 A-1400 Vienna, Austria COMPILATION AND EVALUATION OF FISSION YIELD NUCLEAR DATA IAEA, VIENNA, 2000 IAEA-TECDOC-1168 ISSN 1011–4289 © IAEA, 2000 Printed by the IAEA in Austria December 2000 FOREWORD Fission product yields are required at several stages of the nuclear fuel cycle and are therefore included in all large international data files for reactor calculations and related applications. Such files are maintained and disseminated by the Nuclear Data Section of the IAEA as a member of an international data centres network. Users of these data are from the fields of reactor design and operation, waste management and nuclear materials safeguards, all of which are essential parts of the IAEA programme. In the 1980s, the number of measured fission yields increased so drastically that the manpower available for evaluating them to meet specific user needs was insufficient. To cope with this task, it was concluded in several meetings on fission product nuclear data, some of them convened by the IAEA, that international co-operation was required, and an IAEA co-ordinated research project (CRP) was recommended. This recommendation was endorsed by the International Nuclear Data Committee, an advisory body for the nuclear data programme of the IAEA. As a consequence, the CRP on the Compilation and Evaluation of Fission Yield Nuclear Data was initiated in 1991, after its scope, objectives and tasks had been defined by a preparatory meeting.
    [Show full text]
  • The Electronuclear Conversion of Fertile to Fissile Material
    UCRL-52144 THE ELECTRONUCLEAR CONVERSION OF FERTILE TO FISSILE MATERIAL C. M. Van Atta J. D. Lee H. Heckrotto October 11, 1976 Prepared for U.S. Energy Research & Development Administration under contract No. W-7405-Eng-48 II\M LAWRENCE lUg LIVERMORE k^tf LABORATORY UnrmsilyotCatftxna/lJvofmofe s$ PC DISTRIBUTION OF THIS DOCUMENmmT IS UMUMWTED NOTICE Thii npoit WM prepared w u account of wot* •pomond by UM Uiilttd Stalwi GovcmiMM. Nittim Uw United Stain nor the United Statn Energy tUwardi it Development AdrnWrtrtUon, not «y of thei* employee!, nor any of their contricton, •ubcontrecton, or their employe*!, makti any warranty, expreai « Implied, or muMi any toga) liability oc reeponafctUty for the accuracy, completenni or uMfulntat of uy Information, apperatui, product or proem dlecloead, or repreienl. that tu UM would not *nfrkig» prrrtt*)}MWiwd r%hl». NOTICE Reference to a oompmy or product rum don not imply approval or nconm ndatjon of the product by the Untnrtity of California or the US. Energy Research A Devetopnient Administration to the uchvton of others that may be suitable. Printed In the United Stitei or America Available from National Technical Information Service U.S. Department of Commerce 528S Port Royal Road Springfield, VA 22161 Price: Printed Copy S : Microfiche $2.25 DMimtic P»t» Ranflt PHca *•#» Rtnft MM 001-025 $ 3.50 326-350 10.00 026-050 4.00 351-375 10.50 051-075 4.50 376-400 10.75 076-100 5.00 401-425 11.00 101-125 5.50 426-450 31.75 126-150 6.00 451-475 12.00 151-175 6.75 476-500 12.50 176-200 7.50 501-525 12.75 201-225 7.75 526-550 13.00 526-250 8.00 551-575 13.50 251-275 9.00 576-600 I3.7S 276-300 9.25 601 -up 301-325 9.75 *Ml J2.50 fot «ch iddltlOMl 100 pip tacmitMt from 601 ID 1,000 flfcK IM 54.50 for eicli iMUknal I0O plfe feenmMI om 1,000 p*o.
    [Show full text]
  • Arxiv:1901.01410V3 [Astro-Ph.HE] 1 Feb 2021 Mental Information Is Available, and One Has to Rely Strongly on Theoretical Predictions for Nuclear Properties
    Origin of the heaviest elements: The rapid neutron-capture process John J. Cowan∗ HLD Department of Physics and Astronomy, University of Oklahoma, 440 W. Brooks St., Norman, OK 73019, USA Christopher Snedeny Department of Astronomy, University of Texas, 2515 Speedway, Austin, TX 78712-1205, USA James E. Lawlerz Physics Department, University of Wisconsin-Madison, 1150 University Avenue, Madison, WI 53706-1390, USA Ani Aprahamianx and Michael Wiescher{ Department of Physics and Joint Institute for Nuclear Astrophysics, University of Notre Dame, 225 Nieuwland Science Hall, Notre Dame, IN 46556, USA Karlheinz Langanke∗∗ GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany and Institut f¨urKernphysik (Theoriezentrum), Fachbereich Physik, Technische Universit¨atDarmstadt, Schlossgartenstraße 2, 64298 Darmstadt, Germany Gabriel Mart´ınez-Pinedoyy GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany; Institut f¨urKernphysik (Theoriezentrum), Fachbereich Physik, Technische Universit¨atDarmstadt, Schlossgartenstraße 2, 64298 Darmstadt, Germany; and Helmholtz Forschungsakademie Hessen f¨urFAIR, GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany Friedrich-Karl Thielemannzz Department of Physics, University of Basel, Klingelbergstrasse 82, 4056 Basel, Switzerland and GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany (Dated: February 2, 2021) The production of about half of the heavy elements found in nature is assigned to a spe- cific astrophysical nucleosynthesis process: the rapid neutron capture process (r-process). Although this idea has been postulated more than six decades ago, the full understand- ing faces two types of uncertainties/open questions: (a) The nucleosynthesis path in the nuclear chart runs close to the neutron-drip line, where presently only limited experi- arXiv:1901.01410v3 [astro-ph.HE] 1 Feb 2021 mental information is available, and one has to rely strongly on theoretical predictions for nuclear properties.
    [Show full text]
  • Two-Proton Radioactivity 2
    Two-proton radioactivity Bertram Blank ‡ and Marek P loszajczak † ‡ Centre d’Etudes Nucl´eaires de Bordeaux-Gradignan - Universit´eBordeaux I - CNRS/IN2P3, Chemin du Solarium, B.P. 120, 33175 Gradignan Cedex, France † Grand Acc´el´erateur National d’Ions Lourds (GANIL), CEA/DSM-CNRS/IN2P3, BP 55027, 14076 Caen Cedex 05, France Abstract. In the first part of this review, experimental results which lead to the discovery of two-proton radioactivity are examined. Beyond two-proton emission from nuclear ground states, we also discuss experimental studies of two-proton emission from excited states populated either by nuclear β decay or by inelastic reactions. In the second part, we review the modern theory of two-proton radioactivity. An outlook to future experimental studies and theoretical developments will conclude this review. PACS numbers: 23.50.+z, 21.10.Tg, 21.60.-n, 24.10.-i Submitted to: Rep. Prog. Phys. Version: 17 December 2013 arXiv:0709.3797v2 [nucl-ex] 23 Apr 2008 Two-proton radioactivity 2 1. Introduction Atomic nuclei are made of two distinct particles, the protons and the neutrons. These nucleons constitute more than 99.95% of the mass of an atom. In order to form a stable atomic nucleus, a subtle equilibrium between the number of protons and neutrons has to be respected. This condition is fulfilled for 259 different combinations of protons and neutrons. These nuclei can be found on Earth. In addition, 26 nuclei form a quasi stable configuration, i.e. they decay with a half-life comparable or longer than the age of the Earth and are therefore still present on Earth.
    [Show full text]
  • 2.3 Neutrino-Less Double Electron Capture - Potential Tool to Determine the Majorana Neutrino Mass by Z.Sujkowski, S Wycech
    DEPARTMENT OF NUCLEAR SPECTROSCOPY AND TECHNIQUE 39 The above conservatively large systematic hypothesis. TIle quoted uncertainties will be soon uncertainty reflects the fact that we did not finish reduced as our analysis progresses. evaluating the corrections fully in the current analysis We are simultaneously recording a large set of at the time of this writing, a situation that will soon radiative decay events for the processes t e'v y change. This result is to be compared with 1he and pi-+eN v y. The former will be used to extract previous most accurate measurement of McFarlane the ratio FA/Fv of the axial and vector form factors, a et al. (Phys. Rev. D 1984): quantity of great and longstanding interest to low BR = (1.026 ± 0.039)'1 I 0 energy effective QCD theory. Both processes are as well as with the Standard Model (SM) furthermore very sensitive to non- (V-A) admixtures in prediction (Particle Data Group - PDG 2000): the electroweak lagLangian, and thus can reveal BR = (I 038 - 1.041 )*1 0-s (90%C.L.) information on physics beyond the SM. We are currently analyzing these data and expect results soon. (1.005 - 1.008)* 1W') - excl. rad. corr. Tale 1 We see that even working result strongly confirms Current P1IBETA event sxpelilnentstatistics, compared with the the validity of the radiative corrections. Another world data set. interesting comparison is with the prediction based on Decay PIBETA World data set the most accurate evaluation of the CKM matrix n >60k 1.77k element V d based on the CVC hypothesis and ihce >60 1.77_ _ _ results
    [Show full text]
  • Advanced Reactors with Innovative Fuels
    Nuclear Science Advanced Reactors with Innovative Fuels Workshop Proceedings Villigen, Switzerland 21-23 October 1998 NUCLEAR•ENERGY•AGENCY OECD, 1999. Software: 1987-1996, Acrobat is a trademark of ADOBE. All rights reserved. OECD grants you the right to use one copy of this Program for your personal use only. Unauthorised reproduction, lending, hiring, transmission or distribution of any data or software is prohibited. You must treat the Program and associated materials and any elements thereof like any other copyrighted material. All requests should be made to: Head of Publications Service, OECD Publications Service, 2, rue AndrÂe-Pascal, 75775 Paris Cedex 16, France. OECD PROCEEDINGS Proceedings of the Workshop on Advanced Reactors with Innovative Fuels hosted by Villigen, Switzerland 21-23 October 1998 NUCLEAR ENERGY AGENCY ORGANISATION FOR ECONOMIC CO-OPERATION AND DEVELOPMENT ORGANISATION FOR ECONOMIC CO-OPERATION AND DEVELOPMENT Pursuant to Article 1 of the Convention signed in Paris on 14th December 1960, and which came into force on 30th September 1961, the Organisation for Economic Co-operation and Development (OECD) shall promote policies designed: − to achieve the highest sustainable economic growth and employment and a rising standard of living in Member countries, while maintaining financial stability, and thus to contribute to the development of the world economy; − to contribute to sound economic expansion in Member as well as non-member countries in the process of economic development; and − to contribute to the expansion of world trade on a multilateral, non-discriminatory basis in accordance with international obligations. The original Member countries of the OECD are Austria, Belgium, Canada, Denmark, France, Germany, Greece, Iceland, Ireland, Italy, Luxembourg, the Netherlands, Norway, Portugal, Spain, Sweden, Switzerland, Turkey, the United Kingdom and the United States.
    [Show full text]
  • Alpha-Decay Chains of Z=122 Superheavy Nuclei Using Cubic Plus Proximity Potential with Improved Transfer Matrix Method
    Indian Journal of Pure & Applied Physics Vol. 58, May 2020, pp. 397-403 Alpha-decay chains of Z=122 superheavy nuclei using cubic plus proximity potential with improved transfer matrix method G Naveyaa, S Santhosh Kumarb, S I A Philominrajc & A Stephena* aDepartment of Nuclear Physics, University of Madras, Guindy Campus, Chennai 600 025, India bDepartment of Physics, Kanchi Mamunivar Centre for Post Graduate Studies, Lawspet, Puducherry 605 008, India cDepartment of Physics, Madras Christian College, Chennai 600 059, India Received 4 May 2020 The alpha decay chain properties of Z = 122 isotope in the mass range 298 A 350, even-even nuclei, are studied using a fission-like model with an effective combination of the cubic plus proximity potential in the pre and post-scission regions, wherein the decay rates are calculated using improved transfer matrix method, and the results are in good agreement with other phenomenological formulae such as Universal decay law, Viola-Seaborg, Royer, etc. The nuclear ground-state masses are taken from WS4 mass model. The next minimum in the half-life curves of the decay chain obtained at N=186,178 & 164 suggest the shell closure at N=184, 176 & 162 which coincides well with the predictions of two-centre shell model approach. This study also unveils that the isotopes 298-300, 302, 304-306, 308-310, 312,314122 show 7, 5, 4, 3, 2 and 1 decay chain, respectively. All the other isotopes from A = 316 to 350 may undergo spontaneous fission since the obtained SF half -lives are comparatively less. The predictions in the present study may have an impact in the experimental synthesis and detection of the new isotopes in near future.
    [Show full text]
  • Prospects for Measurements with Strange Hadrons at Lhcb
    Prospects for measurements with strange hadrons at LHCb A. A. Alves Junior1, M. O. Bettler2, A. Brea Rodr´ıguez1, A. Casais Vidal1, V. Chobanova1, X. Cid Vidal1, A. Contu3, G. D'Ambrosio4, J. Dalseno1, F. Dettori5, V.V. Gligorov6, G. Graziani7, D. Guadagnoli8, T. Kitahara9;10, C. Lazzeroni11, M. Lucio Mart´ınez1, M. Moulson12, C. Mar´ınBenito13, J. Mart´ınCamalich14;15, D. Mart´ınezSantos1, J. Prisciandaro 1, A. Puig Navarro16, M. Ramos Pernas1, V. Renaudin13, A. Sergi11, K. A. Zarebski11 1Instituto Galego de F´ısica de Altas Enerx´ıas(IGFAE), Santiago de Compostela, Spain 2Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom 3INFN Sezione di Cagliari, Cagliari, Italy 4INFN Sezione di Napoli, Napoli, Italy 5Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom, now at Universit`adegli Studi di Cagliari, Cagliari, Italy 6LPNHE, Sorbonne Universit´e,Universit´eParis Diderot, CNRS/IN2P3, Paris, France 7INFN Sezione di Firenze, Firenze, Italy 8Laboratoire d'Annecy-le-Vieux de Physique Th´eorique , Annecy Cedex, France 9Institute for Theoretical Particle Physics (TTP), Karlsruhe Institute of Technology, Kalsruhe, Germany 10Institute for Nuclear Physics (IKP), Karlsruhe Institute of Technology, Kalsruhe, Germany 11School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom 12INFN Laboratori Nazionali di Frascati, Frascati, Italy 13Laboratoire de l'Accelerateur Lineaire (LAL), Orsay, France 14Instituto de Astrof´ısica de Canarias and Universidad de La Laguna, Departamento de Astrof´ısica, La Laguna, Tenerife, Spain 15CERN, CH-1211, Geneva 23, Switzerland 16Physik-Institut, Universit¨atZ¨urich,Z¨urich,Switzerland arXiv:1808.03477v2 [hep-ex] 31 Jul 2019 Abstract This report details the capabilities of LHCb and its upgrades towards the study of kaons and hyperons.
    [Show full text]
  • Problem Set 3 Solutions
    22.01 Fall 2016, Problem Set 3 Solutions October 9, 2016 Complete all the assigned problems, and do make sure to show your intermediate work. 1 Activity and Half Lives 1. Given the half lives and modern-day abundances of the three natural isotopes of uranium, calculate the isotopic fractions of uranium when the Earth first formed 4.5 billion years ago. Today, uranium consists of 0.72% 235U, 99.2745% 238U, and 0.0055% 234U. However, it is clear that the half life of 234U (245,500 years) is so short compared to the lifetime of the Earth (4,500,000,000 years) that it would have all decayed away had there been some during the birth of the Earth. Therefore, we look a little closer, and find that 234U is an indirect decay product of 238U, by tracing it back from its parent nuclides on the KAERI table: α β− β− 238U −! 234T h −! 234P a −! 234U (1) Therefore we won’t consider there being any more 234U than would normally be in equi­ librium with the 238U around at the time. We set up the two remaining equations as follows: −t t ;235 −t t ;238 = 1=2 = 1=2 N235 = N0235 e N238 = N0238 e (2) Using the current isotopic abundances from above as N235 and N238 , the half lives from n 9 t 1 1 the KAERI Table of Nuclides t =2;235 = 703800000 y; t =2;238 = 4:468 · 10 y , and the lifetime of the earth in years (keeping everything in the same units), we arrive at the following expressions for N0235 and N0238 : N235 0:0072 N238 0:992745 N0235 =−t = 9 = 4:307N0238 =−t = 9 = 2:718 (3) =t1 ;235 −4:5·10 =7:038·108 =t1 ;238 −4:5·10 =4:468·109 e =2 e e =2 e Finally, taking the ratios of these two relative abundances gives us absolute abundances: 4:307 2:718 f235 = = 0:613 f238 = = 0:387 (4) 4:307 + 2:718 4:307 + 2:718 235U was 61.3% abundant, and 238U was 38.7% abundant.
    [Show full text]