DOCSLIB.ORG

Astronomy 112: the Physics of Stars Class 10 Notes: Applications and Extensions of Polytropes in the Last Class We Saw That Poly

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Astronomy 112: the Physics of Stars Class 10 Notes: Applications and Extensions of Polytropes in the Last Class We Saw That Poly Astronomy 112: The Physics of Stars Class 10 Notes: Applications and Extensions of Polytropes In the last class we saw that polytropes are a simple approximation to a full solution to the stellar structure equations, which, despite their simplicity, yield important physical insight. This is particularly true for certain types of stars, such as white dwarfs and very low mass stars. In today’s class we will explore further extensions and applications of simple polytropic models, which we can in turn use to generate our first realistic models of typical main sequence stars. I. The Binding Energy of Polytropes We will begin by showing that any realistic model must have n < 5. Of course we already determined that solutions to the Lane-Emden equation reach Θ = 0 at finite ξ only for n < 5, which already hints that n ≥ 5 is a problem. Nonetheless, we have not shown that, as a matter of physical principle, models of this sort are unacceptable for stars. To demonstrate this, we will prove a generally useful result about the energy content of polytropic stars. As a preliminary to this, we will write down the polytropic relation (n+1)/n P = KP ρ in a slightly different form. Consider a polytropic star, and imagine moving down within it to the point where the pressure is larger by a small amount dP . The corre- sponding change in density dρ obeys n + 1 dP = K ρ1/ndρ. P n Similarly, since P = K ρ1/n, ρ P it follows that P ! K 1 dP ! d = P ρ(1−n)/ndρ = ρ n n + 1 ρ We can regard this relation as telling us how much the ratio of pressure to density changes when we move through a star by an amount such that the pressure alone changes by dP . With this out of the way, we now compute the gravitational potential energy of a polytropic star of total mass M and radius R. For convenience, since we’ll be changing variables many times, we will write limits of integration as s for surface or c for center, 1 indicating that, whatever variable we’re using, it is to be evaluated at the surface or the center. The potential energy is Z s Gm Ω = − dm c r 1 Z s G = − d(m2) 2 c r "Gm2 #s 1 Z s Gm2 = − − 2 dr 2r c 2 c r GM 2 1 Z s Gm2 = − − dr 2R 2 c r2 In the third step, we integrated by parts. Next, we use the equation of hydrostatic balance, dP/dr = −Gmρ/r2, or dP = −(Gm/r)(ρ/r) dr to replace Gm/r in the integral, and then make use of the result we just derived: GM 2 1 Z s dP Ω = − + m 2R 2 c ρ GM 2 n + 1 Z s P ! = − + m d . 2R 2 c ρ Now we integrate by parts one more time: GM 2 "n + 1 P #s n + 1 Z s P Ω = − + m − dm 2R 2 ρ c 2 c ρ GM 2 n + 1 Z s P = − − 4πr2ρ dr 2R 2 c ρ GM 2 n + 1 Z s 4π = − − P d(r3). 2R 2 c 3 In the second step, the term in brackets vanishes because m = 0 at the center and P/ρ = 0 at the surface. Finally, one last integration by parts, followed by another application of hydrostatic balance: GM 2 n + 1 4π s n + 1 Z s Ω = − − P r3 + 4πr3 dP 2R 2 3 c 6 c GM 2 n + 1 Z s Gm = − − 4πr3 ρ dr 2R 6 c r2 GM 2 n + 1 Z s Gm = − − dm 2R 6 c r As before, the term in brackets vanished in the second step because r = 0 at the center and P = 0 at the surface. 2 Notice that we have gotten back to where we started: the integral on the right hand side is just −Ω. Thus we have shown that GM 2 n + 1 Ω = − + Ω 2R 6 3 GM 2 Ω = − . 5 − n R Given this result, one can get the total energy simply by applying the virial theorem. If the star consists of monotonic ideal gas, we have 1 3 GM 2 E = Ω + U = Ω = − . 2 10 − 2n R This is a handy formula to know, but it also shows us why only polytropic models with n < 5 are acceptable models for stars. At n = 5, the total energy of the polytrope becomes infinite, and for n > 5 the energy E > 0, meaning the object is unbound. Thus only models with n < 5 represent gravitationally bound objects with finite binding energy. II. Radiation Pressure and the Eddington Limit Polytropes are very useful, but, since they separate the hydrostatic balance of a star (as embodied by the first two stellar structure equations) from its energy balance (as embodied by the second two), they have limitations. In particular, they cannot by themselves tell us anything about how energy flows through a star, and thus about stars’ luminosities. To put this into our models, we must re-insert the temperature- dependence. This brings back into the picture the third structure equation: dT 3 κρ F dT 3 κ F = − = − . dr 4ac T 3 4πr2 dm 4ac T 3 (4πr2)2 We care about the temperature is because of its relationship with the pressure, and in particular with the pressure of radiation. That is because the gas pressure follows 4 Pgas ∝ T , but radiation pressure has a much steeper dependence: Prad = aT /3. Thus at sufficiently high temperatures radiation pressure always dominates. You calculated when radiation pressure begins to dominate on your last homework. The strong dependence of Prad on T has important consequences for stellar structure. To see this, it is helpful to rewrite our last equation in terms of radiation pressure rather than temperature: dT 3 κρ F = − dr 4ac T 3 4πr2 4 dT κρ F aT 3 = − 3 dr c 4πr2 dP κρ F rad = − dr c 4πr2 3 Repeating the same trick using the Lagrangian form gives dP κ F rad = − . dm c (4πr2)2 Now consider what this implies for hydrostatic balance. Since P = Pgas + Prad, the equation of hydrostatic balance can be written as dP dP Gm rad + gas = −ρ dr dr r2 dP Gm dP rad = −ρ − gas dr r2 dr Since density and temperature always fall with radius within a star, dPgas/dr is always negative, so the term −dPgas/dr > 0. Thus we have dP Gm rad > −ρ dr r2 κρ F Gm − > −ρ c 4πr2 r2 ! 2 −1 ! 4πcGm 4 M 0.4 cm g F < = 3.2 × 10 L , κ M κ where we have normalized κ to the electron scattering opacity because that is usually the smallest possible opacity in a star, producing the maximum possible F . This result is known as the Eddington limit, named after Arthur Eddington, who first derived it. In his honor, the quantity on the right-hand side is called the Eddington luminosity: 4πcGm L = . Edd κ This result represents a fundamental limit on the luminosity of any object in hydro- static equilibrium. It applies to stars, but it applies equally well to any other type of astronomical system, and the Eddington limit is important for black holes, entire galaxies, and in many other contexts. This also lets us derive a useful relation describing how the ratio of radiation pressure to total pressure varies within a star. We have already shown that dP κρ F rad = − dr c 4πr2 dP Gm = −ρ , dr r2 and taking the ratio of these two equations gives dP κF F rad = = . dP 4πcGm LEdd 4 The Eddington limit also tells us something about nuclear energy generation at the center of a star, where m = 0 and F (m) = 0. We can Taylor expand F around m = 0, so F ≈ m(dF/dm). Inserting this into our inequality gives dF 4πcG = q < , dm c κ where we have noted that the final stellar structure equation asserts that dF/dm = q. Thus we have derived an upper limit on the rate of nuclear energy generation qc in the center of a star. There is an important subtlety here, which is important to notice. Our equation relating dT/dr and F is calculated assuming that F comes solely from radiation, i.e. that there are no other sources of energy transport in stars. This means that the F that appears in the limit includes only the radiative heat flow F , not any other sources of heat transport – and we will see next week that there is potentially another type of energy transport that is important in some stars. Although the radiative heat flow always obeys the limit we have derived, the total heat flow need not. This is obviously not much a limitation at the surface of a star, since there radiation is the only means by which energy can move around. III. The Eddington Model Considering the importance of radiation pressure leads to an important model, essen- tially the first quasi-realistic model for stellar structure. It was first derived by Arthur Eddington, and is therefore known as the Eddington model. The first step in this model is the equation we just derived for the relation between dP κF F rad = = . dP 4πcGm LEdd Eddington then assumes that the right hand side is constant. This might seem like a crazy assumption, but it turns out to be reasonably good. You will show that it holds for massive stars on your homework.
Load more

Recommended publications
  • Nuclear Astrophysics
    Nuclear Astrophysics Lecture 3 Thurs. Nov. 3, 2011 Prof. Shawn Bishop, Office 2013, Ex. 12437 www.nucastro.ph.tum.de 1 Summary of Results Thus Far 2 Alternative expressions for Pressures is the number of atoms of atomic species with atomic number “z” in the volume V Mass density of each species is just: where are the atomic mass of species “z” and Avogadro’s number, respectively Mass fraction, in volume V, of species “z” is just And clearly, Collect the algebra to write And so we have for : If species “z” can be ionized, the number of particles can be where is the number of free particles produced by species “z” (nucleus + free electrons). If fully ionized, and 3 The mean molecular weight is defined by the quantity: We can write it out as: is the average of for atomic species Z > 2 For atomic species heavier than helium, average atomic weight is and if fully ionized, Fully ionized gas: Same game can be played for electrons: 4 Temp. vs Density Plane Relativistic - Relativistic Non g cm-3 5 Thermodynamics of the Gas 1st Law of Thermodynamics: Thermal energy of the system (heat) Total energy of the system Assume that , then Substitute into dQ: Heat capacity at constant volume: Heat capacity at constant pressure: We finally have: 6 For an ideal gas: Therefore, And, So, Let’s go back to first law, now, for ideal gas: using For an isentropic change in the gas, dQ = 0 This leads to, after integration of the above with dQ = 0, and 7 First Law for isentropic changes: Take differentials of but Use Finally Because g is constant, we can integrate
    [Show full text]
  • Mass – Luminosity Relation for Massive Stars
    MASS – LUMINOSITY RELATION FOR MASSIVE STARS Within the Eddington model β ≡ Pg/P = const, and a star is an n = 3 polytrope. Large mass stars have small β, and hence are dominated by radiation pressure, and the opacity in them is dominated by electron scattering. Let us consider the outer part of such a star assuming it is in a radiative equilibrium. We have the equation of hydrostatic equilibrium: dP GM = − r ρ, (s2.1) dr r2 and the equation of radiative equilibrium dP κρL r = − r . (s2.2) dr 4πcr2 Dividing these equations side by side we obtain dP κL r = r , (s2.3) dP 4πcGMr Near the stellar surface we have Mr ≈ M and Lr ≈ L, and adopting κ ≈ κe = const, we may integrate equation (s2.3) to obtain κeLr Pr − Pr,0 = (P − P0) , (s2.4) 4πcGMr 4 where Pr,0 = P0 = aTeff /6 is the radiation pressure at the surface, i.e. at τ = 0, where the gas pressure Pg = 0. At a modest depth below stellar surface pressure is much larger than P0, we may neglect the integration constants in (s2.4) to obtain P κ L L 1+ X M⊙ L 1 − β = r = e = = , (s2.5) P 4πcGM LEdd 65300 L⊙ M where LEdd is the Eddington luminosity. Equation (s2.5) gives a relation between stellar mass, luminosity and β. The Eddington model gives a relation between stellar mass and β : 1 2 M 18.1 (1 − β) / = 2 2 , (s2.6) M⊙ µ β where µ is a mean molecular weight in units of mass of a hydrogen atom, µ−1 =2X +0.75Y +0.5Z, and X,Y,Z, are the hydrogen, helium, and heavy element abundance by mass fraction.
    [Show full text]
  • Testing Quantum Gravity with LIGO and VIRGO
    Testing Quantum Gravity with LIGO and VIRGO Marek A. Abramowicz1;2;3, Tomasz Bulik4, George F. R. Ellis5 & Maciek Wielgus1 1Nicolaus Copernicus Astronomical Center, ul. Bartycka 18, 00-716, Warszawa, Poland 2Physics Department, Gothenburg University, 412-96 Goteborg, Sweden 3Institute of Physics, Silesian Univ. in Opava, Bezrucovo nam. 13, 746-01 Opava, Czech Republic 4Astronomical Observatory Warsaw University, 00-478 Warszawa, Poland 5Mathematics Department, University of Cape Town, Rondebosch, Cape Town 7701, South Africa We argue that if particularly powerful electromagnetic afterglows of the gravitational waves bursts detected by LIGO-VIRGO will be observed in the future, this could be used as a strong observational support for some suggested quantum alternatives for black holes (e.g., firewalls and gravastars). A universal absence of such powerful afterglows should be taken as a sug- gestive argument against such hypothetical quantum-gravity objects. If there is no matter around, an inspiral-type coalescence (merger) of two uncharged black holes with masses M1, M2 into a single black hole with the mass M3 results in emission of grav- itational waves, but no electromagnetic radiation. The maximal amount of the gravitational wave 2 energy E=c = (M1 + M2) − M3 that may be radiated from a merger was estimated by Hawking [1] from the condition that the total area of all black hole horizons cannot decrease. Because the 2 2 2 horizon area is proportional to the square of the black hole mass, one has M3 > M2 + M1 . In the 1 1 case of equal initial masses M1 = M2 = M, this yields [ ], E 1 1 h p i = [(M + M ) − M ] < 2M − 2M 2 ≈ 0:59: (1) Mc2 M 1 2 3 M From advanced numerical simulations (see, e.g., [2–4]) one gets, in the case of comparable initial masses, a much more stringent energy estimate, ! EGRAV 52 M 2 ≈ 0:03; meaning that EGRAV ≈ 1:8 × 10 [erg]: (2) Mc M The estimate assumes validity of Einstein’s general relativity.
    [Show full text]
  • Ultraluminous X-Ray Pulsars
    Ultraluminous X-ray pulsars: the high-B interpretation Juri Poutanen (University of Turku, Finland; IKI, Moscow) Sergey Tsygankov, Alexander Mushtukov, Valery Suleimanov, Alexander Lutovinov, Anna Chashkina, Pavel Abolmasov Plan: • ULX before 2014 • A short history of ULXPs • Supercritical accretion onto a magnetized neutron star • Large or low B? Propeller? • Beamed? • Winds? Models for ULX (before 2014) • Super-Eddington accretion onto a stellar-mass black hole (e.g. King 2001, Begelman et al. 2006, Poutanen et al. 2007) • Sub-Eddington accretion onto intermediate mass black holes (Colbert & Mushotzky 2001) • Young rotation-powered pulsar (Medvedev & Poutanen 2013) Super-Eddington accretion • Slim disk models Accretion rate is large, but most of the released energy is advected towards the BH. ˙ ˙ M (r) =M 0 • Super-disks with winds Accretion rate is large, but most of the mass is blown away by radiation. Only the Eddington rate goes to the BH. ˙ ˙ r M (r) =M 0 Rsph ˙ ˙ M (rin ) =M Edd M˙ R R 0 - spherization radius sph ≈ in ˙ M Edd Shakura & Sunyaev 1973 Super-Eddington accretion • Slim disk models Accretion rate is large, but most of the released energy is advected towards the BH. ˙ ˙ M (r) =M 0 • Super-disks with winds Accretion rate is large, but most of the mass is blown away by radiation. Only the Eddington rate goes to the BH. ! ! r M (r) =M 0 Rsph ! ! M(rin ) =M Edd M! R ≈ R 0 -spherization radius sph S ! M Edd Ohsuga et al. 2005 Super-Eddington accretion Super-disks with winds and advection Accretion rate is large, a lot of mass is blown away by radiation (using fraction εW of available radiative flux), but still a significant fraction goes to the BH.
    [Show full text]
  • 20 — Polytropes [Revision : 1.1]
    20 — Polytropes [Revision : 1.1] • Mechanical Equations – So far, two differential equations for stellar structure: ∗ hydrostatic equilibrium: dP GM = −ρ r dr r2 ∗ mass-radius relation: dM r = 4πr2ρ dr – Two equations involve three unknowns: pressure P , density ρ, mass variable Mr — cannot solve – Try to relate P and ρ using a gas equation of state — e.g., ideal gas: ρkT P = µ ...but this introduces extra unknown: temperature T – To eliminate T , must consider energy transport • Polytropic Equation-of-State – Alternative to having to do full energy transport – Used historically to create simple stellar models – Assume some process means that pressure and density always related by polytropic equation of state P = Kργ for constant K, γ – Polytropic EOS resembles pressure-density relation for adibatic change; but γ is not necessarily equal to usual ratio of specific heats – Physically, gases that follow polytropic EOS are either ∗ Degenerate — Fermi-Dirac statistics apply (e.g., non-relativistic degenerate gas has P ∝ ρ5/3) ∗ Have some ‘hand-wavy’ energy transport process that somehow maintains a one-to- one pressure-density relation • Polytropes – A polytrope is simplified stellar model constructed using polytropic EOS – To build such a model, first write down hydrostatic equilibrium equation in terms of gradient of graqvitational potential: dP dΦ = −ρ dr dr – Eliminate pressure using polytropic EOS: K dργ dΦ = − ρ dr dr – Rearrange: Kγ dργ−1 dΦ = − γ − 1 dr dr – Solving: K(n + 1)ρ1/n = −Φ where n ≡ 1/(γ − 1) is the polytropic index (do not
    [Show full text]
  • Exceeding the Eddington Limit
    The Fate of the Most Massive Stars ASP Conference Series, Vol. 332, 2005 Roberta M. Humphreys and Krzysztof Z. Stanek Exceeding the Eddington Limit Nir J. Shaviv Racah Institute of Physics, Hebrew University of Jerusalem, Jerusalem 91904, Israel Abstract. We review the current theory describing the existence of steady state super-Eddington atmospheres. The key to the understanding of these at- mospheres is the existence of a porous layer responsible for a reduced e®ective opacity. We show how porosity arises from radiative-hydrodynamic instabili- ties and why the ensuing inhomogeneities reduce the e®ective opacity. We then discuss the appearance of these atmospheres. In particular, one of their funda- mental characteristic is the continuum driven acceleration of a thick wind from regions where the inhomogeneities become transparent. We end by discussing the role that these atmospheres play in the evolution of massive stars. 1. Introduction The notion that astrophysical objects can remain in a super-Eddington steady state for considerable amounts of time, contradicts the common wisdom usually invoked in which the classical Eddington limit, Edd, cannot be exceeded in a steady state because no hydrostatic solution canLthen exist. In other words, if objects do pass Edd, they are expected to be highly dynamic. A huge mass loss should ensueLsince large parts of their atmospheres are then gravitationally unbound and should therefore be expelled. ´ Carinae, and classical novae for that matter, stand in contrast to the above notion. ´ Car was super-Eddington (hereafter SED) during its 20 year long eruption (Davidson and Humphreys 1997). Yet, its observed mass loss and velocity are inconsistent with any standard solution (Shaviv 2000).
    [Show full text]
  • Stellar Structure — Polytrope Models for White Dwarf Density Profiles and Masses
    Stellar Structure | Polytrope models for White Dwarf density profiles and masses We assume that the star is spherically symmetric. Then we want to calculate the mass density ρ(r) (units of kg/m3) as a function of distance r from its centre. The mass density will be highest at its centre and as the distance from the centre increases the density will decrease until it becomes very low in the outer atmosphere of the star. At some point ρ(r) will reach some low cutoff value and then we will say that that value of r is the radius of the star. The mass dnesity profile is calculated from two coupled differential equations. The first comes from conservation of mass. It is dm(r) = 4πr2ρ(r); (1) dr where m(r) is the total mass within a sphere of radius r. Note that m(r ! 1) = M, the total mass of the star is that within a sphere large enough of include the whole star. In practice the density profile ρ(r) drops off rapidly in the outer atmosphere of the star and so can obtain M from m(r) at some value of r large enough that the density ρ(r) has become small. Also, of course if r = 0, then m = 0: the mass inside a sphere of 0 radius is 0. Thus the one boundary condition we need for this first-order ODE is m(r = 0) = 0. The second equation comes from a balance of forces on a spherical shell at a radius r. The pull of gravity on the shell must equal the outward pressure at equilibrium; see Ref.
    [Show full text]
  • Homologous Stellar Models and Polytropes Equation of State, Mean
    Homologous Stellar Models and Polytropes Equation of State, Mean Molecular Weight and Opacity Homologous Models and Lane-Emden Equation Comparison Between Polytrope and Real Models Main Sequence Stars Post-Main Sequence Hydrogen-Shell Burning Post-Main Sequence Helium-Core Burning White Dwarfs, Massive and Neutron Stars Introduction The equations of stellar structure are coupled differential equations which, along with supplementary equations or data (equation of state, opacity and nuclear energy generation) need to be solved numerically. Useful insight can be gained, however, using analytical methods in- volving some simple assumptions. One approach is to assume that stellar models are homologous; • that is, all physical variables in stellar interiors scale the same way with the independent variable measuring distance from the stellar centre (the interior mass at some point specified by M(r)). The scaling factor used is the stellar mass (M). A second approach is to suppose that at some distance r from • the stellar centre, the pressure and density are related by P (r) = K ργ where K is a constant and γ is related to some polytropic index n through γ = (n + 1)/n. Substituting in the equations of hydrostatic equilibrium and mass conservation then leads to the Lane-Emden equation which can be solved for a specific poly- tropic index n. Equation of State Stellar gas is an ionised plasma, where the density is so high that the average particle 15 spacing is of the order of an atomic radius (10− m): An equation of state of the form • P = P (ρ, T, composition) defines pressure as needed to solve the equations of stellar structure.
    [Show full text]
  • Polytropes Astrophysics and Space Science Library
    POLYTROPES ASTROPHYSICS AND SPACE SCIENCE LIBRARY VOLUME 306 EDITORIAL BOARD Chairman W.B. BURTON, National Radio Astronomy Observatory, Charlottesville, Virginia, U.S.A. ([email protected]); University of Leiden, The Netherlands ([email protected]) Executive Committee J. M. E. KUIJPERS, Faculty of Science, Nijmegen, The Netherlands E. P. J. VAN DEN HEUVEL, Astronomical Institute, University of Amsterdam, The Netherlands H. VAN DER LAAN, Astronomical Institute, University of Utrecht, The Netherlands MEMBERS I. APPENZELLER, Landessternwarte Heidelberg-Königstuhl, Germany J. N. BAHCALL, The Institute for Advanced Study, Princeton, U.S.A. F. BERTOLA, Universitá di Padova, Italy J. P. CASSINELLI, University of Wisconsin, Madison, U.S.A. C. J. CESARSKY, Centre d'Etudes de Saclay, Gif-sur-Yvette Cedex, France O. ENGVOLD, Institute of Theoretical Astrophysics, University of Oslo, Norway R. McCRAY, University of Colorado, JILA, Boulder, U.S.A. P. G. MURDIN, Institute of Astronomy, Cambridge, U.K. F. PACINI, Istituto Astronomia Arcetri, Firenze, Italy V. RADHAKRISHNAN, Raman Research Institute, Bangalore, India K. SATO, School of Science, The University of Tokyo, Japan F. H. SHU, University of California, Berkeley, U.S.A. B. V. SOMOV, Astronomical Institute, Moscow State University, Russia R. A. SUNYAEV, Space Research Institute, Moscow, Russia Y. TANAKA, Institute of Space & Astronautical Science, Kanagawa, Japan S. TREMAINE, CITA, Princeton University, U.S.A. N. O. WEISS, University of Cambridge, U.K. POLYTROPES Applications in Astrophysics and Related Fields by G.P. HOREDT Deutsches Zentrum für Luft- und Raumfahrt DLR, Wessling, Germany KLUWER ACADEMIC PUBLISHERS NEW YORK, BOSTON, DORDRECHT, LONDON, MOSCOW eBook ISBN: 1-4020-2351-0 Print ISBN: 1-4020-2350-2 ©2004 Springer Science + Business Media, Inc.
    [Show full text]
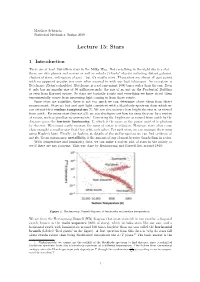
  • Lecture 15: Stars
    Matthew Schwartz Statistical Mechanics, Spring 2019 Lecture 15: Stars 1 Introduction There are at least 100 billion stars in the Milky Way. Not everything in the night sky is a star there are also planets and moons as well as nebula (cloudy objects including distant galaxies, clusters of stars, and regions of gas) but it's mostly stars. These stars are almost all just points with no apparent angular size even when zoomed in with our best telescopes. An exception is Betelgeuse (Orion's shoulder). Betelgeuse is a red supergiant 1000 times wider than the sun. Even it only has an angular size of 50 milliarcseconds: the size of an ant on the Prudential Building as seen from Harvard square. So stars are basically points and everything we know about them experimentally comes from measuring light coming in from those points. Since stars are pointlike, there is not too much we can determine about them from direct measurement. Stars are hot and emit light consistent with a blackbody spectrum from which we can extract their surface temperature Ts. We can also measure how bright the star is, as viewed from earth . For many stars (but not all), we can also gure out how far away they are by a variety of means, such as parallax measurements.1 Correcting the brightness as viewed from earth by the distance gives the intrinsic luminosity, L, which is the same as the power emitted in photons by the star. We cannot easily measure the mass of a star in isolation. However, stars often come close enough to another star that they orbit each other.
    [Show full text]
  • A Supercomputer Models a Blinking, Impossibly Bright 'Monster Pulsar' 8 September 2016
    A supercomputer models a blinking, impossibly bright 'monster pulsar' 8 September 2016 this case X-rays) emitted by this luminous gas are what astronomers actually observe. But as the photons travel away from the center, they push against the incoming gas, slowing the flow of gas towards the center. This force is called the radiation pressure force. As more gas falls onto the object, it becomes hotter and brighter, but if it becomes too bright the radiation pressure slows the infalling gas so much that it creates a "traffic jam." This traffic jam limits the rate at which new gas can add additional energy to the system and prevents it from getting any brighter. This luminosity upper limit, at which the radiation pressure balances the Artist’s impression of the “New Lighthouse Model.”. gravitational force, is called the Eddington Credit: NAOJ luminosity. The central energy source of enigmatic pulsating Ultra Luminous X-ray sources (ULX) could be a neutron star according to numerical simulations performed by a research group led by Tomohisa Kawashima at the National Astronomical Observatory of Japan (NAOJ). ULXs, which are remarkably bright X-ray sources, were thought to be powered by black holes. But in 2014, the X-ray space telescope "NuSTAR" detected unexpected periodic pulsed emissions in a ULX named M82 X-2. The discovery of this object named "ULX-pulsar" has puzzled The new lighthouse model (a snapshot from Movie 1) and simulation results from the present research (inset astrophysicists. Black holes can be massive on the right.) In the simulation results, the red indicates enough to provide the energy needed to create stronger radiation, and the arrows show the directions of ULXs, but black holes shouldn't be able to produce photon flow.
    [Show full text]
  • Models of Hydrostatic Magnetar Atmospheres at High Luminosities
    Models of hydrostatic atmospheres of magnetars at high luminosities Thijs van Putten1 Anna Watts1, Caroline D’Angelo1, Matthew Baring2, Chryssa Kouveliotou3 1University of Amsterdam, 2Rice University, 3NASA/Marshall Space Flight Center arXiv:1208.4212 October 30 2012, Fermi Symposium, Monterey image © Don Dixon Magnetars ✤ Neutron stars with inferred dipole magnetic field B ~ 1013-1016 G. ✤ Exhibit pulses (X-ray & radio), soft gamma ray bursts (~1040 erg s-1) and giant flares (~1044 erg s-1). image © NASA Magnetar atmosphere models Thijs van Putten October 30 2012 Magnetar model ✤ What is the equation of state? ✤ How and where is the emission created? ✤ What is the magnetic field configuration? Thompson & Duncan (1995) Magnetar atmosphere models Thijs van Putten October 30 2012 A peculiar magnetar burst Fermi GBM light curve of August 2008 burst from SGR 0501+4516. Light curve and black body fits of X2127 (Smale 2001) Magnetar atmosphere models Thijs van Putten October 30 2012 Photospheric Radius Expansion in magnetars? ✤ PRE in magnetars seems qualitatively possible (Watts et al. 2010) if magnetars have: ✤ Emission from optically thick region ✤ A critical luminosity ✤ Photosphere cooling with expansion ✤ Opacity increasing with radius Fermi GBM light curve of August 2008 burst from SGR 0501+4516. ✤ Observing it would constrain EoS, B and the emission location. Magnetar atmosphere models Thijs van Putten October 30 2012 Nonmagnetic models 0.9999 ✤ PRE requires sequence of extended stable atmospheres. ✤ Nonmagnetic models made by 0.9998 Paczynski & Anderson (1986). Luminosity / Eddington luminosity 0.0002 0.1 1 10 100 Atmosphere height (km) ✤ Stable nonmagnetic atmospheres exist up to r = 200 km.
    [Show full text]