DOCSLIB.ORG

Lecture 5-3: Applications Polytrope Models

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 5-3: Applications Polytrope Models Lecture 5-3: Applications polytrope models Literature: MWW Chapter 19 !" 1 g) Eddington’s standard model In this model, the energy equation and equation of diffusive radiative transfer are included (approximately) to arrive at simple solutions. In essence, this model boils down assuming a constant b throughout the star. We looked at this in section 5a. From a slightly different angle, with b is constant we have Prad/P is constant: 2 d lnT 3 Pκ Lr ∇ = = 4 d ln P 64πσ T GMr 4 P dPrad with Prad = 4σT 3c we can write: ∇ = 4Prad dP dP κL L L rad = r dP 4πcGM Mr M Introduce, ε ≡ dLr dMr r ε(r) = ∫ ε dMr Mr =Lr Mr 0 L L η(r) ≡ ε(r) ε(R) = r Mr M dP L rad = κ(r)η(r) dP 4πcGM 3 L Prad (r) = κ (r)η(r) P(r) with 4πcGM P(r) κ (r)η(r) = ∫ κη dP P(r), and we have, 0 L 1− β = κ (r)η(r) 4πcGM Now, realize that κ decreases rapidly inwards while η decreases rapidly outwards for main sequence stars. Eddington assumed that β is constant and that results in a simple T - P or T - ρ relation. 1/3 # 3ck 1− β & 1/3 T (r) = % ( ρ (r) $ 4σµmu β ' 4 4 1/3 P k T (! k $ 3 1− β + gas ρ * ( )- 4/3 P(r) = = = # & 4 ρ (r), see slide 4 lecture 5-1 m m a β µ u β )*"µ u % β ,- The constant in brackets is also equal to the constant K in slide 8 lecture 5-1 1/3 4π GM 2/3 K n = 3 = ( ) , or ( ) 2 1/3 4 ( 4 ! + *ξ (−θ3 ) - ) ,ξ1 2 1− β 4 ! M $ 4 = 0.002996µ # & , and β " Mo % 2/3 ! M $ T (r) = 4.62 ×106 βµ# & ρ1/3 (r) " Mo % but note β and M in this T - ρ relation5 are not independent One-parameter family of models: β decreases with increasing M Other properties: ρc = 54.18ρ " %2 4 17 M " RO % 2 Pc =1.242 ×10 $ ' $ ' dyne/cm # MO & # R & " % 6 M " RO % Tc =19.72 ×10 βµ $ '$ ' K # MO &# R & T = 0.5852Tc Standard model provides the run of density, temperature, and pressure. For absolute values, we need to provide stellar mass and radius. i.e., M & R ⇒ ρ ⇒ ρ and hence ρ r , T r , P r are set c ( ) ( ) ( ) as the constant K in the pressure density relation is not specified aforehand in the standard model. E.g., the 2 combination µ M sets β and hence K but then there are still an infinite number of solutions corresponding6 to different R. m≈0.6 Inner region well approximated by a polytrope of index 3. Outer region is convective and better approximated by a polytrope of index 1.5 (but this is only 0.6% of the mass) 7 The Eddington Solar model 8 h) Completely convective stars Examples: late M dwarfs cool, gravitationally contracting stars Internal Structure Consider case with ∇ = ∇ a d = ( Γ 2 − 1 ) / Γ 2 everywhere in the star 1 1+ 1 Then: P = K ρ n or P = K ! T n + 1 with n = (effective polytropic index) Γ2 −1 If Γ2 constant ⇒ completely convective star: polytrope of index n Useful specific case: ideal gas ⇒ n = 3/2 (§5-2, slides 8-10) ⇒ 1/3 " M % " R % ρc = 5.991ρ K = 2.476 ×1014 $ ' $ ' 2 4 # MO & # RO & " M % " R % P = 8.658×1015 O dyne/cm2 1/2 3/2 c $ ' $ ' 0.0796 " M % " R % # MO & # R & K( = $ O ' $ O ' µ 5/2 # M & # R & " % 7 M " RO % Tc =1.234 ×10 µ$ '$ ' K # MO &# R & Radial behavior of ρ,P,T T = 0.5306Tc 9 follows from Lane-Emden function: θ3/2 i) Hayahsi track Hayashi track: Location of low-mass (<3 Mo), fully convective stars in the Hertzsprung-Russell diagram. Relevant for low-mass protostars, red giants, and asymptotic red giants. Match fully convective stellar structure models with boundary conditions for the photosphere. Assume the star is fully convective (polytrope with n=3/2) with a thin radiative outer layer where the opacity is dominated by H–. 10 dP dτ dP g = −gρ and = −κρ or = dr dr dτ κ Assume κ is constant, 2g GM P(τ = 2 3) = with g = 2 3κ R k 0.5 7.7 −25 0.5 with P = ρT, κ=κoρ T , and κo =10 Z we have, µmu 1.5 8.7 2µmu G M ρ T = 2 3k κo R 11 For a polytrope with n = 3 2 we have, ! $3/2 ρ T 3M µmu GM = # & , ρc = 5.99ρ = 5.99 2 , and Tc = 0.539 ρc "Tc % 4π R k R 2.25 3.25 10.95 Tc 2µmu G M 0.1!µmuG $ 1.75 0.25 T = 1.5 2 ≈ # & M R ρc 3k κo R κo " k % We assume that convection starts at the photosphere (T = Teff ) 2 4 and use L = 4π R σTeff to replace R 3.25 11.45 0.07 !µmuG $ 1.75 1/8 T ≈ 1/8 # & M L κoσ " k % 0.15 0.01 ! M $ ! L $ ! 0.02 $0.04 Teff ≈ 2000# & # & # & K; actually, ≈ 3000 K " Mo % " Lo % " Z % 12 Summary Fully convective stars (with a radiative atmosphere) of a given mass and composition in hydrostatic equilibrium lie at a constant (low) effective temperature independent of luminosity. Conversely, the effective temperature is nearly independent of how the luminosity is generated. Objects to the right of these Hayashi tracks have too steep a temperature gradient and convection will set in. Convection quickly sets the adiabatic temperature gradient (lecture 3-3, slide 14). That quickly rearranges the stellar structure and the star will settle on the Hayashi track. 13 j) protostars & the Hayashi track Premain sequence evolution: Molecular cloud core collapses on a slow timescale (t~1/(Gr)1/2). When the core becomes optically thick, the internal temperature rises (virial theorem) and molecules (e.g., H2) will dissociate, and then H and He will ionize. Rps M 5 ≈ 50 , and T ≈ 10 K (virial theorem) R M o o No nuclear reactions. High luminosity and high opacity. Protostar is fully convective except for an H– dominated atmosphere. Star will start high up on the Hayashi track. As it contracts, the radius will decrease but the effective temperature stays constant. 14 3GM 2 dR E = −E = E / 2 and L = E! = −E! 2 ≈ t i g t g 7R2 dt 2 4 with L = 4π R σTeff , we then have: 1 dR 28πσT 4 = eff , which integrates to (T ≈ cst): R4 dt 3GM 2 eff 2 2/3 GM #τ KH & t = 4 3 and L = L0 % ( 28πσTeff R $ 3t ' 2 2 4 where Ro = R(t = τ KH 3) with τ KH = 3GM 7RoL0 and L0 = 4π R0σTeff 15 Radiative (Henyey) protostellar tracks d lnT 3κ P L Convection will stop when ∇ = = R < 0.4 rad d ln P 64GπσT 4 M As the star contracts, the luminosity will drop and radiative energy transport will take over in the core 4 Note that Pc Tc does not decrease (slide 10 of section 5.2). 3 −3.5 T ∝ M R and ρ ∝ M R and κ ∝ ρT and adopt dT dr = Tc R L ∝ M 5.5R−0.5 The star evolves now towards the left in the HR diagram with a slowly increasing luminosity. 16 Summary A protostar will initially be fully convective and contract on a Hayashi track of (almost) constant effective temperature. Eventually, the core will become radiative, the star will switch to a Henyey track and the luminosity will (moderately) increase. As the star contracts, the central temperature will increase (Virial theorem). Eventually, H- burning will be ignited in the core and the star will settle on the main sequence. The timescale for this is set by the Kelvin Helmholtz timescale and this is set for when the star evolves the slowest (eg., near the main sequence). 17 18 Protostellar tracks (solid lines) for different protostellar stellar masses. Isochrones are indicated by dashed lines. The solid lines crossing the tracks indicate the region of D-burning and Li-burning. 19 k) White dwarfs A white dwarf is the stellar remnant of a low mass star with a mass typically half that of the Sun but a radius comparable to the Earth, corresponding to a density of 106 g/cm3. The star is pressure-supported by a degenerate electron gas with (cf., Lecture 3-2 slide 14): 5/3 P = K ρ µ non-relativistic NR ( e ) 4/3 P = KER (ρ µe ) extremely relativistic where the constants Ki only depend on atomic physics The mechanical properties are controlled by the electrons while the thermal energy is stored in the ions. We can use polytropes of index 3/2 and 3 to describe them. 20 Mass-radius relation For the non-relativistic equation of state, we find (Lecture 5-2, slide 8): 1/3 3 2 M R = cst and ρ ∝ M R ∝ M Thus, a more massive white dwarf has to be smaller and will be denser than a less massive white dwarf. Eventually when the density is high enough, the electron gas will become relativistic (cf., lecture 3-2 slide 25) and we have: " %3/2 " %3/2 KER hc 1 M ≈ $ 4/3 ' ≈ 0.197$ 4/3 ' 2 # 0.3639µe G & #Gmu & µe Chandrasekhar mass 5.86 Mch = 2 Mo ≈ 1.46Mo for C, O, ... composition 21 µe Heuristically: Mass-radius relation When analyzing stars using the virial theorem, we discovered that stars are unstable when g<4/3 (lecture 2 slide 11).
Load more

Recommended publications
  • Arxiv:2007.13451V2 [Gr-Qc] 24 Nov 2020 on GR and Its Modifications [31–33], but Also Delivers Model Particles As Well As Dark Matter Candidates [56– Drawbacks
    Early evolutionary tracks of low-mass stellar objects in modified gravity Aneta Wojnar1, ∗ 1Laboratory of Theoretical Physics, Institute of Physics, University of Tartu, W. Ostwaldi 1, 50411 Tartu, Estonia Using a simple model of low-mass stellar objects we have shown modified gravity impact on their early evolution, such as Hayashi tracks, radiative core development, effective temperature, masses, and luminosities. We have also suggested that the upper mass' limit of fully convective stars on the Main Sequence might be different than commonly adopted. I. INTRODUCTION is, in the so-called mass gap [38]), which merged with a black hole of 23M , provided even more questions for Working on modified gravity does not make one to for- theoretical physics of compact objects. get the elegance and success of Einstein's theory of grav- However, it turns out that there is a class of stellar ity, being already confirmed by many observations [1]; objects, with the internal structure much better under- even more, General Relativity (GR) still delights when stood than that of neutron stars, which might be used to one of its mysterious predictions, such as the existence of constrain theories of gravity. It is a family of low-mass black holes, is directly affirmed by the finding of gravi- stars (LMS) [39{41] which includes such ordinary objects tational waves as a result of black holes' binary mergers as M dwarfs (also called red dwarfs), which are cool Main [2] as well as soon after the imaging of the shadow of the Sequence stars with masses in the range [0:09 − 0:6]M , supermassive black hole of M87 [3] (see [4] for a review).
    [Show full text]
  • Revisiting the Pre-Main-Sequence Evolution of Stars I. Importance of Accretion Efficiency and Deuterium Abundance ?
    Astronomy & Astrophysics manuscript no. Kunitomo_etal c ESO 2018 March 22, 2018 Revisiting the pre-main-sequence evolution of stars I. Importance of accretion efficiency and deuterium abundance ? Masanobu Kunitomo1, Tristan Guillot2, Taku Takeuchi,3,?? and Shigeru Ida4 1 Department of Physics, Nagoya University, Furo-cho, Chikusa-ku, Nagoya, Aichi 464-8602, Japan e-mail: [email protected] 2 Université de Nice-Sophia Antipolis, Observatoire de la Côte d’Azur, CNRS UMR 7293, 06304 Nice CEDEX 04, France 3 Department of Earth and Planetary Sciences, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8551, Japan 4 Earth-Life Science Institute, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8551, Japan Received 5 February 2016 / Accepted 6 December 2016 ABSTRACT Context. Protostars grow from the first formation of a small seed and subsequent accretion of material. Recent theoretical work has shown that the pre-main-sequence (PMS) evolution of stars is much more complex than previously envisioned. Instead of the traditional steady, one-dimensional solution, accretion may be episodic and not necessarily symmetrical, thereby affecting the energy deposited inside the star and its interior structure. Aims. Given this new framework, we want to understand what controls the evolution of accreting stars. Methods. We use the MESA stellar evolution code with various sets of conditions. In particular, we account for the (unknown) efficiency of accretion in burying gravitational energy into the protostar through a parameter, ξ, and we vary the amount of deuterium present. Results. We confirm the findings of previous works that, in terms of evolutionary tracks on the Hertzsprung-Russell (H-R) diagram, the evolution changes significantly with the amount of energy that is lost during accretion.
    [Show full text]
  • Nuclear Astrophysics
    Nuclear Astrophysics Lecture 3 Thurs. Nov. 3, 2011 Prof. Shawn Bishop, Office 2013, Ex. 12437 www.nucastro.ph.tum.de 1 Summary of Results Thus Far 2 Alternative expressions for Pressures is the number of atoms of atomic species with atomic number “z” in the volume V Mass density of each species is just: where are the atomic mass of species “z” and Avogadro’s number, respectively Mass fraction, in volume V, of species “z” is just And clearly, Collect the algebra to write And so we have for : If species “z” can be ionized, the number of particles can be where is the number of free particles produced by species “z” (nucleus + free electrons). If fully ionized, and 3 The mean molecular weight is defined by the quantity: We can write it out as: is the average of for atomic species Z > 2 For atomic species heavier than helium, average atomic weight is and if fully ionized, Fully ionized gas: Same game can be played for electrons: 4 Temp. vs Density Plane Relativistic - Relativistic Non g cm-3 5 Thermodynamics of the Gas 1st Law of Thermodynamics: Thermal energy of the system (heat) Total energy of the system Assume that , then Substitute into dQ: Heat capacity at constant volume: Heat capacity at constant pressure: We finally have: 6 For an ideal gas: Therefore, And, So, Let’s go back to first law, now, for ideal gas: using For an isentropic change in the gas, dQ = 0 This leads to, after integration of the above with dQ = 0, and 7 First Law for isentropic changes: Take differentials of but Use Finally Because g is constant, we can integrate
    [Show full text]
  • Single Star Implementation Notes
    Mon. Not. R. Astron. Soc. 000, 000{000 (0000) Printed 8 November 2017 (MN LATEX style file v2.2) Single Star Implementation Notes PFH 8 November 2017 1 METHODS 1=2 − 1 times the cloud diameter Lcloud) are driven as an Ornstein-Uhlenbeck process in Fourier space, with the com- Our simulations use GIZMO (?),1, and include full self- pressive part of the modes projected out via Helmholtz de- gravity, adaptive resolution, ideal and non-ideal magneto- composition so that we can specify the ratio of compress- hydrodynamics (MHD), detailed cooling and heating ible and incompressible/solenoidal modes. Unless otherwise physics, protostar formation, accretion, and feedback in the specified we adopt pure solenoidal driving, appropriate for form of protostellar jets and radiative heating, and main- e.g. galactic shear (so that we do not artificially \force" com- sequence stellar feedback in the form of photo-ionization pression/collapse), but we vary this. The specific implemen- and photo-electric heating, radiation pressure, stellar winds, tation here has been verified in ????. and supernovae. A subset of our runs include explicit treat- The driving specifies the large-scale steady-state (one- ment of the dust particle and cosmic ray dynamics as well dimensional) turbulent velocity σ ≡ hv2 i1=2 and as radiation-hydrodynamics; otherwise these are included in 1D turb; 1D Mach number M ≡ h(v =c )2i1=2, where v is simplified form. turb; 1D s turb; 1D an (arbitrary) projection (in detail we average over all 1.1 Gravity random projections). Unless otherwise specified, we initial- ize our clouds on the linewidth-size relation from ?, with All our simulations include full self-gravity for gas, stars, −1 1=2 σ1D ≈ 0:7 km s (Lcloud=pc) and dust.
    [Show full text]
  • Useful Constants
    Appendix A Useful Constants A.1 Physical Constants Table A.1 Physical constants in SI units Symbol Constant Value c Speed of light 2.997925 × 108 m/s −19 e Elementary charge 1.602191 × 10 C −12 2 2 3 ε0 Permittivity 8.854 × 10 C s / kgm −7 2 μ0 Permeability 4π × 10 kgm/C −27 mH Atomic mass unit 1.660531 × 10 kg −31 me Electron mass 9.109558 × 10 kg −27 mp Proton mass 1.672614 × 10 kg −27 mn Neutron mass 1.674920 × 10 kg h Planck constant 6.626196 × 10−34 Js h¯ Planck constant 1.054591 × 10−34 Js R Gas constant 8.314510 × 103 J/(kgK) −23 k Boltzmann constant 1.380622 × 10 J/K −8 2 4 σ Stefan–Boltzmann constant 5.66961 × 10 W/ m K G Gravitational constant 6.6732 × 10−11 m3/ kgs2 M. Benacquista, An Introduction to the Evolution of Single and Binary Stars, 223 Undergraduate Lecture Notes in Physics, DOI 10.1007/978-1-4419-9991-7, © Springer Science+Business Media New York 2013 224 A Useful Constants Table A.2 Useful combinations and alternate units Symbol Constant Value 2 mHc Atomic mass unit 931.50MeV 2 mec Electron rest mass energy 511.00keV 2 mpc Proton rest mass energy 938.28MeV 2 mnc Neutron rest mass energy 939.57MeV h Planck constant 4.136 × 10−15 eVs h¯ Planck constant 6.582 × 10−16 eVs k Boltzmann constant 8.617 × 10−5 eV/K hc 1,240eVnm hc¯ 197.3eVnm 2 e /(4πε0) 1.440eVnm A.2 Astronomical Constants Table A.3 Astronomical units Symbol Constant Value AU Astronomical unit 1.4959787066 × 1011 m ly Light year 9.460730472 × 1015 m pc Parsec 2.0624806 × 105 AU 3.2615638ly 3.0856776 × 1016 m d Sidereal day 23h 56m 04.0905309s 8.61640905309
    [Show full text]
  • Astronomy 112: the Physics of Stars Class 10 Notes: Applications and Extensions of Polytropes in the Last Class We Saw That Poly
    Astronomy 112: The Physics of Stars Class 10 Notes: Applications and Extensions of Polytropes In the last class we saw that polytropes are a simple approximation to a full solution to the stellar structure equations, which, despite their simplicity, yield important physical insight. This is particularly true for certain types of stars, such as white dwarfs and very low mass stars. In today’s class we will explore further extensions and applications of simple polytropic models, which we can in turn use to generate our first realistic models of typical main sequence stars. I. The Binding Energy of Polytropes We will begin by showing that any realistic model must have n < 5. Of course we already determined that solutions to the Lane-Emden equation reach Θ = 0 at finite ξ only for n < 5, which already hints that n ≥ 5 is a problem. Nonetheless, we have not shown that, as a matter of physical principle, models of this sort are unacceptable for stars. To demonstrate this, we will prove a generally useful result about the energy content of polytropic stars. As a preliminary to this, we will write down the polytropic relation (n+1)/n P = KP ρ in a slightly different form. Consider a polytropic star, and imagine moving down within it to the point where the pressure is larger by a small amount dP . The corre- sponding change in density dρ obeys n + 1 dP = K ρ1/ndρ. P n Similarly, since P = K ρ1/n, ρ P it follows that P ! K 1 dP ! d = P ρ(1−n)/ndρ = ρ n n + 1 ρ We can regard this relation as telling us how much the ratio of pressure to density changes when we move through a star by an amount such that the pressure alone changes by dP .
    [Show full text]
  • 20 — Polytropes [Revision : 1.1]
    20 — Polytropes [Revision : 1.1] • Mechanical Equations – So far, two differential equations for stellar structure: ∗ hydrostatic equilibrium: dP GM = −ρ r dr r2 ∗ mass-radius relation: dM r = 4πr2ρ dr – Two equations involve three unknowns: pressure P , density ρ, mass variable Mr — cannot solve – Try to relate P and ρ using a gas equation of state — e.g., ideal gas: ρkT P = µ ...but this introduces extra unknown: temperature T – To eliminate T , must consider energy transport • Polytropic Equation-of-State – Alternative to having to do full energy transport – Used historically to create simple stellar models – Assume some process means that pressure and density always related by polytropic equation of state P = Kργ for constant K, γ – Polytropic EOS resembles pressure-density relation for adibatic change; but γ is not necessarily equal to usual ratio of specific heats – Physically, gases that follow polytropic EOS are either ∗ Degenerate — Fermi-Dirac statistics apply (e.g., non-relativistic degenerate gas has P ∝ ρ5/3) ∗ Have some ‘hand-wavy’ energy transport process that somehow maintains a one-to- one pressure-density relation • Polytropes – A polytrope is simplified stellar model constructed using polytropic EOS – To build such a model, first write down hydrostatic equilibrium equation in terms of gradient of graqvitational potential: dP dΦ = −ρ dr dr – Eliminate pressure using polytropic EOS: K dργ dΦ = − ρ dr dr – Rearrange: Kγ dργ−1 dΦ = − γ − 1 dr dr – Solving: K(n + 1)ρ1/n = −Φ where n ≡ 1/(γ − 1) is the polytropic index (do not
    [Show full text]
  • Astronomy General Information
    ASTRONOMY GENERAL INFORMATION HERTZSPRUNG-RUSSELL (H-R) DIAGRAMS -A scatter graph of stars showing the relationship between the stars’ absolute magnitude or luminosities versus their spectral types or classifications and effective temperatures. -Can be used to measure distance to a star cluster by comparing apparent magnitude of stars with abs. magnitudes of stars with known distances (AKA model stars). Observed group plotted and then overlapped via shift in vertical direction. Difference in magnitude bridge equals distance modulus. Known as Spectroscopic Parallax. SPECTRA HARVARD SPECTRAL CLASSIFICATION (1-D) -Groups stars by surface atmospheric temp. Used in H-R diag. vs. Luminosity/Abs. Mag. Class* Color Descr. Actual Color Mass (M☉) Radius(R☉) Lumin.(L☉) O Blue Blue B Blue-white Deep B-W 2.1-16 1.8-6.6 25-30,000 A White Blue-white 1.4-2.1 1.4-1.8 5-25 F Yellow-white White 1.04-1.4 1.15-1.4 1.5-5 G Yellow Yellowish-W 0.8-1.04 0.96-1.15 0.6-1.5 K Orange Pale Y-O 0.45-0.8 0.7-0.96 0.08-0.6 M Red Lt. Orange-Red 0.08-0.45 *Very weak stars of classes L, T, and Y are not included. -Classes are further divided by Arabic numerals (0-9), and then even further by half subtypes. The lower the number, the hotter (e.g. A0 is hotter than an A7 star) YERKES/MK SPECTRAL CLASSIFICATION (2-D!) -Groups stars based on both temperature and luminosity based on spectral lines.
    [Show full text]
  • Stellar Structure — Polytrope Models for White Dwarf Density Profiles and Masses
    Stellar Structure | Polytrope models for White Dwarf density profiles and masses We assume that the star is spherically symmetric. Then we want to calculate the mass density ρ(r) (units of kg/m3) as a function of distance r from its centre. The mass density will be highest at its centre and as the distance from the centre increases the density will decrease until it becomes very low in the outer atmosphere of the star. At some point ρ(r) will reach some low cutoff value and then we will say that that value of r is the radius of the star. The mass dnesity profile is calculated from two coupled differential equations. The first comes from conservation of mass. It is dm(r) = 4πr2ρ(r); (1) dr where m(r) is the total mass within a sphere of radius r. Note that m(r ! 1) = M, the total mass of the star is that within a sphere large enough of include the whole star. In practice the density profile ρ(r) drops off rapidly in the outer atmosphere of the star and so can obtain M from m(r) at some value of r large enough that the density ρ(r) has become small. Also, of course if r = 0, then m = 0: the mass inside a sphere of 0 radius is 0. Thus the one boundary condition we need for this first-order ODE is m(r = 0) = 0. The second equation comes from a balance of forces on a spherical shell at a radius r. The pull of gravity on the shell must equal the outward pressure at equilibrium; see Ref.
    [Show full text]
  • Homologous Stellar Models and Polytropes Equation of State, Mean
    Homologous Stellar Models and Polytropes Equation of State, Mean Molecular Weight and Opacity Homologous Models and Lane-Emden Equation Comparison Between Polytrope and Real Models Main Sequence Stars Post-Main Sequence Hydrogen-Shell Burning Post-Main Sequence Helium-Core Burning White Dwarfs, Massive and Neutron Stars Introduction The equations of stellar structure are coupled differential equations which, along with supplementary equations or data (equation of state, opacity and nuclear energy generation) need to be solved numerically. Useful insight can be gained, however, using analytical methods in- volving some simple assumptions. One approach is to assume that stellar models are homologous; • that is, all physical variables in stellar interiors scale the same way with the independent variable measuring distance from the stellar centre (the interior mass at some point specified by M(r)). The scaling factor used is the stellar mass (M). A second approach is to suppose that at some distance r from • the stellar centre, the pressure and density are related by P (r) = K ργ where K is a constant and γ is related to some polytropic index n through γ = (n + 1)/n. Substituting in the equations of hydrostatic equilibrium and mass conservation then leads to the Lane-Emden equation which can be solved for a specific poly- tropic index n. Equation of State Stellar gas is an ionised plasma, where the density is so high that the average particle 15 spacing is of the order of an atomic radius (10− m): An equation of state of the form • P = P (ρ, T, composition) defines pressure as needed to solve the equations of stellar structure.
    [Show full text]
  • Polytropes Astrophysics and Space Science Library
    POLYTROPES ASTROPHYSICS AND SPACE SCIENCE LIBRARY VOLUME 306 EDITORIAL BOARD Chairman W.B. BURTON, National Radio Astronomy Observatory, Charlottesville, Virginia, U.S.A. ([email protected]); University of Leiden, The Netherlands ([email protected]) Executive Committee J. M. E. KUIJPERS, Faculty of Science, Nijmegen, The Netherlands E. P. J. VAN DEN HEUVEL, Astronomical Institute, University of Amsterdam, The Netherlands H. VAN DER LAAN, Astronomical Institute, University of Utrecht, The Netherlands MEMBERS I. APPENZELLER, Landessternwarte Heidelberg-Königstuhl, Germany J. N. BAHCALL, The Institute for Advanced Study, Princeton, U.S.A. F. BERTOLA, Universitá di Padova, Italy J. P. CASSINELLI, University of Wisconsin, Madison, U.S.A. C. J. CESARSKY, Centre d'Etudes de Saclay, Gif-sur-Yvette Cedex, France O. ENGVOLD, Institute of Theoretical Astrophysics, University of Oslo, Norway R. McCRAY, University of Colorado, JILA, Boulder, U.S.A. P. G. MURDIN, Institute of Astronomy, Cambridge, U.K. F. PACINI, Istituto Astronomia Arcetri, Firenze, Italy V. RADHAKRISHNAN, Raman Research Institute, Bangalore, India K. SATO, School of Science, The University of Tokyo, Japan F. H. SHU, University of California, Berkeley, U.S.A. B. V. SOMOV, Astronomical Institute, Moscow State University, Russia R. A. SUNYAEV, Space Research Institute, Moscow, Russia Y. TANAKA, Institute of Space & Astronautical Science, Kanagawa, Japan S. TREMAINE, CITA, Princeton University, U.S.A. N. O. WEISS, University of Cambridge, U.K. POLYTROPES Applications in Astrophysics and Related Fields by G.P. HOREDT Deutsches Zentrum für Luft- und Raumfahrt DLR, Wessling, Germany KLUWER ACADEMIC PUBLISHERS NEW YORK, BOSTON, DORDRECHT, LONDON, MOSCOW eBook ISBN: 1-4020-2351-0 Print ISBN: 1-4020-2350-2 ©2004 Springer Science + Business Media, Inc.
    [Show full text]
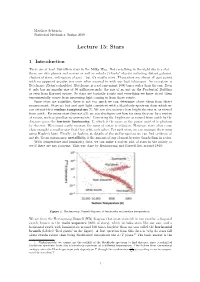
  • Lecture 15: Stars
    Matthew Schwartz Statistical Mechanics, Spring 2019 Lecture 15: Stars 1 Introduction There are at least 100 billion stars in the Milky Way. Not everything in the night sky is a star there are also planets and moons as well as nebula (cloudy objects including distant galaxies, clusters of stars, and regions of gas) but it's mostly stars. These stars are almost all just points with no apparent angular size even when zoomed in with our best telescopes. An exception is Betelgeuse (Orion's shoulder). Betelgeuse is a red supergiant 1000 times wider than the sun. Even it only has an angular size of 50 milliarcseconds: the size of an ant on the Prudential Building as seen from Harvard square. So stars are basically points and everything we know about them experimentally comes from measuring light coming in from those points. Since stars are pointlike, there is not too much we can determine about them from direct measurement. Stars are hot and emit light consistent with a blackbody spectrum from which we can extract their surface temperature Ts. We can also measure how bright the star is, as viewed from earth . For many stars (but not all), we can also gure out how far away they are by a variety of means, such as parallax measurements.1 Correcting the brightness as viewed from earth by the distance gives the intrinsic luminosity, L, which is the same as the power emitted in photons by the star. We cannot easily measure the mass of a star in isolation. However, stars often come close enough to another star that they orbit each other.
    [Show full text]