Lecture 15: Stars
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

X-Ray Sun SDO 4500 Angstroms: Photosphere
ASTR 8030/3600 Stellar Astrophysics X-ray Sun SDO 4500 Angstroms: photosphere T~5000K SDO 1600 Angstroms: upper photosphere T~5x104K SDO 304 Angstroms: chromosphere T~105K SDO 171 Angstroms: quiet corona T~6x105K SDO 211 Angstroms: active corona T~2x106K SDO 94 Angstroms: flaring regions T~6x106K SDO: dark plasma (3/27/2012) SDO: solar flare (4/16/2012) SDO: coronal mass ejection (7/2/2012) Aims of the course • Introduce the equations needed to model the internal structure of stars. • Overview of how basic stellar properties are observationally measured. • Study the microphysics relevant for stars: the equation of state, the opacity, nuclear reactions. • Examine the properties of simple models for stars and consider how real models are computed. • Survey (mostly qualitatively) how stars evolve, and the endpoints of stellar evolution. Stars are relatively simple physical systems Sound speed in the sun Problem of Stellar Structure We want to determine the structure (density, temperature, energy output, pressure as a function of radius) of an isolated mass M of gas with a given composition (e.g., H, He, etc.) Known: r Unknown: Mass Density + Temperature Composition Energy Pressure Simplifying assumptions 1. No rotation à spherical symmetry ✔ For sun: rotation period at surface ~ 1 month orbital period at surface ~ few hours 2. No magnetic fields ✔ For sun: magnetic field ~ 5G, ~ 1KG in sunspots equipartition field ~ 100 MG Some neutron stars have a large fraction of their energy in B fields 3. Static ✔ For sun: convection, but no large scale variability Not valid for forming stars, pulsating stars and dying stars. 4. -

R-Process Elements from Magnetorotational Hypernovae
r-Process elements from magnetorotational hypernovae D. Yong1,2*, C. Kobayashi3,2, G. S. Da Costa1,2, M. S. Bessell1, A. Chiti4, A. Frebel4, K. Lind5, A. D. Mackey1,2, T. Nordlander1,2, M. Asplund6, A. R. Casey7,2, A. F. Marino8, S. J. Murphy9,1 & B. P. Schmidt1 1Research School of Astronomy & Astrophysics, Australian National University, Canberra, ACT 2611, Australia 2ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), Australia 3Centre for Astrophysics Research, Department of Physics, Astronomy and Mathematics, University of Hertfordshire, Hatfield, AL10 9AB, UK 4Department of Physics and Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology, Cambridge, MA 02139, USA 5Department of Astronomy, Stockholm University, AlbaNova University Center, 106 91 Stockholm, Sweden 6Max Planck Institute for Astrophysics, Karl-Schwarzschild-Str. 1, D-85741 Garching, Germany 7School of Physics and Astronomy, Monash University, VIC 3800, Australia 8Istituto NaZionale di Astrofisica - Osservatorio Astronomico di Arcetri, Largo Enrico Fermi, 5, 50125, Firenze, Italy 9School of Science, The University of New South Wales, Canberra, ACT 2600, Australia Neutron-star mergers were recently confirmed as sites of rapid-neutron-capture (r-process) nucleosynthesis1–3. However, in Galactic chemical evolution models, neutron-star mergers alone cannot reproduce the observed element abundance patterns of extremely metal-poor stars, which indicates the existence of other sites of r-process nucleosynthesis4–6. These sites may be investigated by studying the element abundance patterns of chemically primitive stars in the halo of the Milky Way, because these objects retain the nucleosynthetic signatures of the earliest generation of stars7–13. -

Species Which Remained Immutable and Unchanged Thereafter
THE ORIGIN OF THE ELEMENTS BY WILLIAM A. FOWLER CALIFORNIA INSTITUTE OF TECHNOLOGY, PASADENA They [atoms] move in the void and catching each other up jostle together, and some recoil in any direction that may chance, and others become entangled with one another in various degrees according to the symmetry of their shapes and sizes and positions and order, and they remain together and thus the coming into being of composite things is effected. -SIMPLICIUS (6th Century A.D.) It is my privilege to begin our consideration of the history of the universe during this first scientific session of the Academy Centennial with a discussion of the origin of the elements of which the matter of the universe is constituted. The question of the origin of the elements and their numerous isotopes is the modern expression of one of the most ancient problems in science. The early Greeks thought that all matter consisted of the four simple substances-air, earth, fire, and water-and they, too, sought to know the ultimate origin of what for them were the elementary forms of matter. They also speculated that matter consists of very small, indivisible, indestructible, and uncreatable atoms. They were wrong in detail but their concepts of atoms and elements and their quest for origins persist in our science today. When our Academy was founded one century ago, the chemist had shown that the elements were immutable under all chemical and physical transformations known at the time. The alchemist was self-deluded or was an out-and-out charla- tan. Matter was atomic, and absolute immutability characterized each atomic species. -

Luminous Blue Variables
Review Luminous Blue Variables Kerstin Weis 1* and Dominik J. Bomans 1,2,3 1 Astronomical Institute, Faculty for Physics and Astronomy, Ruhr University Bochum, 44801 Bochum, Germany 2 Department Plasmas with Complex Interactions, Ruhr University Bochum, 44801 Bochum, Germany 3 Ruhr Astroparticle and Plasma Physics (RAPP) Center, 44801 Bochum, Germany Received: 29 October 2019; Accepted: 18 February 2020; Published: 29 February 2020 Abstract: Luminous Blue Variables are massive evolved stars, here we introduce this outstanding class of objects. Described are the specific characteristics, the evolutionary state and what they are connected to other phases and types of massive stars. Our current knowledge of LBVs is limited by the fact that in comparison to other stellar classes and phases only a few “true” LBVs are known. This results from the lack of a unique, fast and always reliable identification scheme for LBVs. It literally takes time to get a true classification of a LBV. In addition the short duration of the LBV phase makes it even harder to catch and identify a star as LBV. We summarize here what is known so far, give an overview of the LBV population and the list of LBV host galaxies. LBV are clearly an important and still not fully understood phase in the live of (very) massive stars, especially due to the large and time variable mass loss during the LBV phase. We like to emphasize again the problem how to clearly identify LBV and that there are more than just one type of LBVs: The giant eruption LBVs or h Car analogs and the S Dor cycle LBVs. -

SHELL BURNING STARS: Red Giants and Red Supergiants
SHELL BURNING STARS: Red Giants and Red Supergiants There is a large variety of stellar models which have a distinct core – envelope structure. While any main sequence star, or any white dwarf, may be well approximated with a single polytropic model, the stars with the core – envelope structure may be approximated with a composite polytrope: one for the core, another for the envelope, with a very large difference in the “K” constants between the two. This is a consequence of a very large difference in the specific entropies between the core and the envelope. The original reason for the difference is due to a jump in chemical composition. For example, the core may have no hydrogen, and mostly helium, while the envelope may be hydrogen rich. As a result, there is a nuclear burning shell at the bottom of the envelope; hydrogen burning shell in our example. The heat generated in the shell is diffusing out with radiation, and keeps the entropy very high throughout the envelope. The core – envelope structure is most pronounced when the core is degenerate, and its specific entropy near zero. It is supported against its own gravity with the non-thermal pressure of degenerate electron gas, while all stellar luminosity, and all entropy for the envelope, are provided by the shell source. A common property of stars with well developed core – envelope structure is not only a very large jump in specific entropy but also a very large difference in pressure between the center, Pc, the shell, Psh, and the photosphere, Pph. Of course, the two characteristics are closely related to each other. -
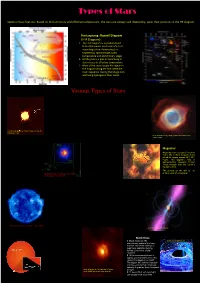
Brown Dwarf: White Dwarf: Hertzsprung -Russell Diagram (H-R
Types of Stars Spectral Classifications: Based on the luminosity and effective temperature , the stars are categorized depending upon their positions in the HR diagram. Hertzsprung -Russell Diagram (H-R Diagram) : 1. The H-R Diagram is a graphical tool that astronomers use to classify stars according to their luminosity (i.e. brightness), spectral type, color, temperature and evolutionary stage. 2. HR diagram is a plot of luminosity of stars versus its effective temperature. 3. Most of the stars occupy the region in the diagram along the line called the main sequence. During that stage stars are fusing hydrogen in their cores. Various Types of Stars Brown Dwarf: White Dwarf: Brown dwarfs are sub-stellar objects After a star like the sun exhausts its nuclear that are not massive enough to sustain fuel, it loses its outer layer as a "planetary nuclear fusion processes. nebula" and leaves behind the remnant "white Since, comparatively they are very cold dwarf" core. objects, it is difficult to detect them. Stars with initial masses Now there are ongoing efforts to study M < 8Msun will end as white dwarfs. them in infrared wavelengths. A typical white dwarf is about the size of the This picture shows a brown dwarf around Earth. a star HD3651 located 36Ly away in It is very dense and hot. A spoonful of white constellation of Pisces. dwarf material on Earth would weigh as much as First directly detected Brown Dwarf HD 3651B. few tons. Image by: ESO The image is of Helix nebula towards constellation of Aquarius hosts a White Dwarf Helix Nebula 6500Ly away. -

Stars IV Stellar Evolution Attendance Quiz
Stars IV Stellar Evolution Attendance Quiz Are you here today? Here! (a) yes (b) no (c) my views are evolving on the subject Today’s Topics Stellar Evolution • An alien visits Earth for a day • A star’s mass controls its fate • Low-mass stellar evolution (M < 2 M) • Intermediate and high-mass stellar evolution (2 M < M < 8 M; M > 8 M) • Novae, Type I Supernovae, Type II Supernovae An Alien Visits for a Day • Suppose an alien visited the Earth for a day • What would it make of humans? • It might think that there were 4 separate species • A small creature that makes a lot of noise and leaks liquids • A somewhat larger, very energetic creature • A large, slow-witted creature • A smaller, wrinkled creature • Or, it might decide that there is one species and that these different creatures form an evolutionary sequence (baby, child, adult, old person) Stellar Evolution • Astronomers study stars in much the same way • Stars come in many varieties, and change over times much longer than a human lifetime (with some spectacular exceptions!) • How do we know they evolve? • We study stellar properties, and use our knowledge of physics to construct models and draw conclusions about stars that lead to an evolutionary sequence • As with stellar structure, the mass of a star determines its evolution and eventual fate A Star’s Mass Determines its Fate • How does mass control a star’s evolution and fate? • A main sequence star with higher mass has • Higher central pressure • Higher fusion rate • Higher luminosity • Shorter main sequence lifetime • Larger -

Nuclear Astrophysics
Nuclear Astrophysics Lecture 3 Thurs. Nov. 3, 2011 Prof. Shawn Bishop, Office 2013, Ex. 12437 www.nucastro.ph.tum.de 1 Summary of Results Thus Far 2 Alternative expressions for Pressures is the number of atoms of atomic species with atomic number “z” in the volume V Mass density of each species is just: where are the atomic mass of species “z” and Avogadro’s number, respectively Mass fraction, in volume V, of species “z” is just And clearly, Collect the algebra to write And so we have for : If species “z” can be ionized, the number of particles can be where is the number of free particles produced by species “z” (nucleus + free electrons). If fully ionized, and 3 The mean molecular weight is defined by the quantity: We can write it out as: is the average of for atomic species Z > 2 For atomic species heavier than helium, average atomic weight is and if fully ionized, Fully ionized gas: Same game can be played for electrons: 4 Temp. vs Density Plane Relativistic - Relativistic Non g cm-3 5 Thermodynamics of the Gas 1st Law of Thermodynamics: Thermal energy of the system (heat) Total energy of the system Assume that , then Substitute into dQ: Heat capacity at constant volume: Heat capacity at constant pressure: We finally have: 6 For an ideal gas: Therefore, And, So, Let’s go back to first law, now, for ideal gas: using For an isentropic change in the gas, dQ = 0 This leads to, after integration of the above with dQ = 0, and 7 First Law for isentropic changes: Take differentials of but Use Finally Because g is constant, we can integrate -

Neutron Stars: Introduction
Neutron Stars: Introduction Stephen Eikenberry 16 Jan 2018 Original Ideas - I • May 1932: James Chadwick discovers the neutron • People knew that n u clei w ere not protons only (nuclear mass >> mass of protons) • Rutherford coined the name “neutron” to describe them (thought to be p+ e- pairs) • Chadwick identifies discrete particle and shows mass is greater than p+ (by 0.1%) • Heisenberg shows that neutrons are not p+ e- pairs Original Ideas - II • Lev Landau supposedly suggested the existence of neutron stars the night he heard of neutrons • Yakovlev et al (2012) show that he in fact discussed dense stars siiltimilar to a gi ant nucl eus BEFORE neutron discovery; this was immediately adapted to “t“neutron s t”tars” Original Ideas - III • 1934: Walter Baade and Fritz Zwicky suggest that supernova eventtttts may create neutron stars • Why? • Suppg(ernovae have huge (but measured) energies • If NS form from normal stars, then the gravitational binding energy gets released • ESN ~ star … Original Ideas - IV • Late 1930s: Oppenheimer & Volkoff develop first theoretical models and calculations of neutron star structure • WldhWould have con tidbttinued, but WWII intervened (and Oppenheimer was busy with other things ) • And that is how things stood for about 30 years … Little Green Men - I • Cambridge experiment with dipole antennae to map cosmic radio sources • PI: Anthony Hewish; grad students included Jocelyn Bell Little Green Men - II • August 1967: CP 1919 discovered in the radio survey • Nov ember 1967: Bell notices pulsations at P =1.337s -

The Potential of Planets Orbiting Red Dwarf Stars to Support Oxygenic Photosynthesis and Complex Life
1 The Potential of Planets Orbiting Red Dwarf Stars to Support Oxygenic Photosynthesis and Complex Life Joseph Gale1 and Amri Wandel2 The Institute of Life Sciences1and The Racach Institute of Physics2, The Hebrew University of Jerusalem, 91904, Israel. [email protected] [email protected] Accepted for publication in the International Journal of Astrobiology Abstract We review and reassess the latest findings on the existence of extra-solar system planets and their potential of having environmental conditions that could support Earth-like life. Within the last two decades, the multi-millennial question of the existence of extra-Solar- system planets has been resolved with the discovery of numerous planets orbiting nearby stars, many of which are Earth-sized (and some even with moderate surface temperatures). Of particular interest in our search for clement conditions for extra-solar system life are planets orbiting Red Dwarf (RD) stars, the most numerous stellar type in the Milky Way galaxy. We show that including RDs as potential life supporting host stars could increase the probability of finding biotic planets by a factor of up to a thousand, and reduce the estimate of the distance to our nearest biotic neighbor by up to 10. We argue that multiple star systems need to be taken into account when discussing habitability and the abundance of biotic exoplanets, in particular binaries of which one or both members are RDs. Early considerations indicated that conditions on RD planets would be inimical to life, as their Habitable Zones (where liquid water could exist) would be so close as to make planets tidally locked to their star. -

Beeps, Flashes, Bangs and Bursts
Beeps, Flashes, Big stars work much faster: Bangs and Bursts. 1,000,000 100,000 100,000 100,000 and Chirps. Forever Peter Watson 3 hours! Live fast, Die Young! Peter Watson, Dept. of Physics Change colour, size, brightness •Vast majority of stars are boring: “main- sequence” (aka middle- class) changing very slowly. •Some oscillate: e.g Cepheids •Large bright stars change by factor 3 in brightness Peter Watson Peter Watson If Stars are large.... • we get supernovae • 6 visible in Milky Way over last 1000 years •well understood: work by blocking mechanism • SN 1006: Brightest •very important since period is proportional to Supernova. intrinsic brightness: • Can see remnants of the expanding •i.e. measure the apparent brightness, the period tells shockwave you the actual brightness, so you know how far away Frank Winkler (Middlebury College) et it is al., AURA, NOAO, NSF Peter Watson Peter Watson Remnant of a very Tycho’s old SN Supernova • Part of the veil nebula in X-rays in Cygnus (1572) Sara Wager NASA / CXC / F.J. Lu (Chinese Academy of Sciences) et al. Peter Watson Peter Watson The Crab (M1) •Recorded by Chinese astronomers "I humbly observe that a guest star has appeared; above the star there is a feeble yellow glimmer. If one examines the divination regarding the Emperor, the interpretation [of the presence of this guest star] is the following: The fact that the star has not overrun Bi and that its brightness must represent a person of great value. I demand that the Office of Historiography is informed of this." PW Peter Watson 1054: Crab •Recorded by Chinese astronomers as “guest star” •May have been recorded by Chaco Indians in New • X-rays (in blue) Mexico • + Optical 4 a.m. -

CHIME and Probing the Origin of Fast Radio Bursts by Liam Dean Connor a Thesis Submitted in Conformity with the Requirements
CHIME and Probing the Origin of Fast Radio Bursts by Liam Dean Connor A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Graduate Department of Astronomy and Astrophysics University of Toronto c Copyright 2016 by Liam Dean Connor Abstract CHIME and Probing the Origin of Fast Radio Bursts Liam Dean Connor Doctor of Philosophy Graduate Department of Astronomy and Astrophysics University of Toronto 2016 The time-variable long-wavelength sky harbours a number of known but unsolved astro- physical problems, and surely many more undiscovered phenomena. With modern tools such problems will become tractable, and new classes of astronomical objects will be revealed. These tools include digital telescopes made from powerful computing clusters, and improved theoretical methods. In this thesis we employ such devices to understand better several puzzles in the time-domain radio sky. Our primary focus is on the origin of fast radio bursts (FRBs), a new class of transients of which there seem to be thousands per sky per day. We offer a model in which FRBs are extragalactic but non-cosmological pulsars in young supernova remnants. Since this theoretical work was done, observations have corroborated the picture of FRBs as young rotating neutron stars, including the non-Poissonian repetition of FRB 121102. We also present statistical arguments regard- ing the nature and location of FRBs. These include reinstituting the classic V=Vmax-test @ log N to measure the brightness distribution of FRBs, i.e., constraining @ log S . We find consis- tency with a Euclidean distribution. This means current observations cannot distinguish between a cosmological population and a more local uniform population, unless added assumptions are made.