Review and Modeling of Crystal Growth of Atropisomers from Solutions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Practical Aspects on How to Deracemize Atropizomers by Means of Crystallization Ryusei Oketani
Practical aspects on how to deracemize atropizomers by means of crystallization Ryusei Oketani To cite this version: Ryusei Oketani. Practical aspects on how to deracemize atropizomers by means of crystallization. Organic chemistry. Normandie Université, 2019. English. NNT : 2019NORMR109. tel-02502796 HAL Id: tel-02502796 https://tel.archives-ouvertes.fr/tel-02502796 Submitted on 9 Mar 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. THÈSE Pour obtenir le diplôme de doctorat Spécialité Chimie Préparée au sein de l’Université de Rouen Normandie Practical aspects on how to deracemize atropisomers by means of crystallization (Aspects pratiques de la déracémisation d'atropisomères par cristallisation) Présentée et soutenue par Ryusei OKETANI Thèse soutenue publiquement le 06 Décembre 2019 devant le jury composé de M. Alexander BREDIKHIN Pr FRC Kazan Scientific Center of RAS Rapporteur M. Joop Ter HORST Pr University of Strathclyde Rapporteur M. Gérard COQUEREL Pr Université de Rouen Normandie Président Mme. Sylvie FERLAY-CHARITAT Pr Université de Strasbourg Examinateur M. Pascal CARDINAEL Pr Université de Rouen Normandie Directeur de thèse Thèse dirigée par Pascal CARDINAEL professeur des universités et Co-encadrée par le Dr. Clément BRANDEL au laboratoire Sciences et Méthodes Séparatives (EA3233 SMS) Contents Contents Contents ......................................................................................................................... -

Characterization of Stereoselective Metabolism, Inhibitory Effect
DMD Fast Forward. Published on November 15, 2018 as DOI: 10.1124/dmd.118.080549 This article has not been copyedited and formatted. The final version may differ from this version. Journal Drug Metabolism and Disposition CHARACTERIZATION OF STEREOSELECTIVE METABOLISM, INHIBITORY EFFECT ON URIC ACID UPTAKE TRANSPORTERS, AND PHARMACOKINETICS OF LESINURAD ATROPISOMERS Downloaded from Chun Yang, Dongmei Zhou, Zancong Shen, David M. Wilson, Matthew Renner, Jeffrey N. Miner, Jean-Luc Girardet and Caroline A. Lee dmd.aspetjournals.org Preclinical & Clinical DMPK (CY, ZS, CAL), Bioanalytical (DZ, DMW), Biology (JM) and Chemistry (J-LG, MR) Ardea Biosciences, Inc., San Diego, CA at ASPET Journals on October 1, 2021 1 DMD Fast Forward. Published on November 15, 2018 as DOI: 10.1124/dmd.118.080549 This article has not been copyedited and formatted. The final version may differ from this version. Running Title: Lesinurad Atropisomer Characterization Corresponding Author: Caroline A. Lee, PhD Downloaded from Translational Sciences, Ardea Biosciences 9390 Towne Centre Drive dmd.aspetjournals.org San Diego, CA 92121 Email: [email protected] at ASPET Journals on October 1, 2021 Tel: 858-449-1797 Manuscript Format Abstract: 223 words Introduction: 599 words Discussion: 1408 words Number of Text Pages: 29 2 DMD Fast Forward. Published on November 15, 2018 as DOI: 10.1124/dmd.118.080549 This article has not been copyedited and formatted. The final version may differ from this version. References: 21 Number of Tables: 2 Number of Figures: 8 Supplemental Table: 0 Supplemental Figures: 0 Downloaded from dmd.aspetjournals.org at ASPET Journals on October 1, 2021 3 DMD Fast Forward. -

Atropisomerism
Atropisomerism Metal-mediated transformations to set biaryl chirality Nathaniel Kadunce Literature Meeting 12 December 2014 Atropisomerism • Atropos- the “inflexible” or “without turn” • Arise from hindered rotation about a single bond allowing for isolation of separate conformers HO2C NO2 HO2C NO2 HO2C NO2 HO2C NO2 Ra Sa 6,6'-dinitro-2,2'-diphenic acid, the first experimentally described atropisomeric compound Journal of the Chemical Society, Transactions 121: 614 First Evidence • Kaufler Hypothesis: cis and trans isomers explain op9cal proper9es • Supported by a series of misassignments in derivave studies • “It has been suggested by Carothers and by Mascarrelli that an objec9on to the Kaufler formula which has never been emphasized is the necessity of bending a bond to an angle of 90°. With a Kekule nucleus such a formula cannot be constructed, and each 9me that chemists adobt assump9ons that cannot be reconciled with the Kekule nucleus they encounter difficul9es.” –Adams, 1933 Rogers, A. and Yuan. H. C. Chem. Rev. 1933, 12, 261. First Evidence • Kaufler Hypothesis: cis and trans isomers explain op9cal proper9es • Supported by a series of misassignments in derivave studies • “It has been suggested by Carothers and by Mascarrelli that an objec9on to the Kaufler formula which has never been emphasized is the necessity of bending a bond to an angle of 90°. With a Kekule nucleus such a formula cannot be constructed, and each 9me that chemists adobt assump9ons that cannot be reconciled with the Kekule nucleus they encounter difficul9es.” –Adams, 1933 -

Atropisomerism: Axial Chirality in Nature and Synthesis
R R * R MLn Me R OH O OH N OMe * Me Me Atropisomerism O * MeO OH N Axial Chirality in Nature and Synthesis H OMe Me MeO O X Y Y X OH O Y X X Y OMe MeO OH Kevin Allan O H MeO * OH Stoltz Group Literature Meeting Al Li Monday 11/14/2005 * O OEt 8 pm OMe 147 Noyes OH O O O O Nu O Nu Outline I. Introduction a. History and Background b. Conditions for Axial Chirality II. Direct Atroposelective Aryl-Aryl Coupling a. Diastereoselective Coupling b. Enantioselective Coupling III. Resolution/Desymmetrization of Prostereogenic Biaryls a. Configurationally Stable, Axially Achiral b. Configurationally Unstable, Axially Chiral Motokazu Uemura (right) and i. Atropodiastereoselective Bridge Formation Ken Kamikawa (left) ii. Atroposelective Bridge Cleavage / The "Lactone Method" Osaka Prefecture University IV. Atroposelective Construction of an Aromatic Ring Albert I. Meyers Colorado State University For a general review of biaryls in synthesis: Bringmann, G.; Mortimer, A. J. P.; Keller, P. A.; Gresser, M. J.; Garner, J.; Breuning, M. Angew. Chem. I. E. 2005, 44, 5384-5427. Biaryl cross-coupling: Stanforth, S. P. Tetrahedron. 1998, 54, 263-303. Lloyd-Williams, P.; Giralt, E. Chem. Soc. Rev. 2001, 30, 145-157. Broutin, P.-E.; Colobert, F. Eur. J. Org. Chem. 2005, 1113-1128. Lactone Methodology: Gerhard Bringmann Matthias Breuning Bringmann, G.; Breuning, M.; Tasler, S. Synthesis, 1999, 4, 525-558. Universitat Wurzburg Universitat Wurzburg Bringmann, G.; Tasler, S.; Pfeifer, R.-M.; Breuning, M. J. Organomet. Chem. 2002, 661, 49-65. Atropisomerism is Everywhere -

Stereochemistry the Different Types of Isomers. Stereochemistry Focuses
Stereochemistry The different types of isomers. Stereochemistry focuses on stereoisomers Stereochemistry, a subdiscipline of chemistry, involves the study of the relative spatial arrangement of atoms that form the structure of molecules and their manipulation. An important branch of stereochemistry is the study of chiral molecules. Stereochemistry is also known as 3D chemistry because the prefix "stereo-" means "three- dimensionality". The study of stereochemistry focuses on stereoisomers and spans the entire spectrum of organic, inorganic, biological, physical and especially supramolecular chemistry. Stereochemistry includes methods for determining and describing these relationships; the effect on the physical or biological properties these relationships impart upon the molecules in question, and the manner in which these relationships influence the reactivity of the molecules in question (dynamic stereochemistry). History Louis Pasteur could rightly be described as the first stereochemist, having observed in 1849 that salts of tartaric acid collected from wine production vessels could rotate plane polarized light, but that salts from other sources did not. This property, the only physical property in which the two types of tartrate salts differed, is due to optical isomerism. In 1874, Jacobus Henricus van 't Hoff and Joseph Le Belexplained optical activity in terms of the tetrahedral arrangement of the atoms bound to carbon. Significance Cahn–Ingold–Prelog priority rules are part of a system for describing a molecule's stereochemistry. They rank the atoms around a stereocenter in a standard way, allowing the relative position of these atoms in the molecule to be described unambiguously. A Fischer projection is a simplified way to depict the stereochemistry around a stereocenter. -

Characterization of Stereoselective Metabolism, Inhibitory Effect on Uric Acid Uptake Transporters, and Pharmacokinetics of Lesinurad Atropisomers
1521-009X/47/2/104–113$35.00 https://doi.org/10.1124/dmd.118.080549 DRUG METABOLISM AND DISPOSITION Drug Metab Dispos 47:104–113, February 2019 Copyright ª 2019 by The American Society for Pharmacology and Experimental Therapeutics Characterization of Stereoselective Metabolism, Inhibitory Effect on Uric Acid Uptake Transporters, and Pharmacokinetics of Lesinurad Atropisomers Chun Yang, Dongmei Zhou, Zancong Shen, David M. Wilson, Matthew Renner, Jeffrey N. Miner, Jean-Luc Girardet, and Caroline A. Lee Preclinical and Clinical DMPK (C.Y., Z.S., C.A.L.), Bioanalytical (D.Z., D.M.W.), Biology (J.N.M.), and Chemistry (M.R., J.-L.G.) Departments, Ardea Biosciences, Inc., San Diego, California Received January 16, 2018; accepted November 2, 2018 ABSTRACT Downloaded from Lesinurad [Zurampic; 2-(5-bromo-4-(4-cyclopropylnaphthalen-1-yl)- There were no significant differences in the plasma protein 4H-1,2,4-triazol-3-ylthio)], a selective inhibitor of uric acid reabsorp- binding among lesinurad and the atropisomers. Following oral tion transporters approved for the treatment of gout, is a racemate administration of 400 mg lesinurad once daily for 14 days to of two atropisomers. The objective of this investigation was to healthy human volunteers, the systemic exposure (Cmax at evaluate the stereoselectivity of metabolism, the inhibitory potency steady state and area under the concentration-time curve from on kidney uric acid reabsorption transporters (URAT1 and OAT4), time zero to the time of dosing interval) of atropisomer 1 was dmd.aspetjournals.org and the clinical pharmacokinetics of the lesinurad atropisomers. approximately 30% lower than that of atropisomer 2, whereas Incubations with human liver microsomes (HLM), recombinant renal clearance was similar. -

Absolute Configuration of 2,2′,3,3′,6- Pentachlorinatedbiphenyl (Pcb 84) Atropisomers
HHS Public Access Author manuscript Author ManuscriptAuthor Manuscript Author Environ Manuscript Author Sci Pollut Res Int Manuscript Author . Author manuscript; available in PMC 2019 June 01. Published in final edited form as: Environ Sci Pollut Res Int. 2018 June ; 25(17): 16402–16410. doi:10.1007/s11356-017-9259-z. ABSOLUTE CONFIGURATION OF 2,2′,3,3′,6- PENTACHLORINATEDBIPHENYL (PCB 84) ATROPISOMERS Xueshu Lia, Sean R. Parkinb, and Hans-Joachim Lehmlera,* aDepartment of Occupational and Environmental Health, College of Public Health, The University of Iowa, Iowa City, IA 52242, USA bDepartment of Chemistry, University of Kentucky, Lexington, KY 40506, USA Abstract Nineteen polychlorinated biphenyl (PCB) congeners, such as 2,2′,3,3′,6-pentachlorobiphenyl (PCB 84), display axial chirality because they form stable rotational isomers, or atropisomers, that are non-superimposable mirror images of each other. Although chiral PCBs undergo atropselective biotransformation and atropselectively alter biological processes, the absolute structure of only a few PCB atropisomers has been determined experimentally. To help close this knowledge gap, pure 2,2′,3,3′,6-pentachlorobiphenyl (PCB 84) atropisomers were obtained by semi-preparative liquid chromatography with two serially connected Nucleodex β-PM columns. The absolute configuration of both atropisomers was determined by X-ray single-crystal diffraction. The PCB 84 atropisomer eluting first and second on the Nucleodex β-PM column correspond to (aR)-(−)- PCB 84 and (aS)-(+)-PCB 84, respectively. Enantioselective gas chromatographic analysis with the β-cyclodextrin-based Chiralsil-Dex CP gas chromatography column showed the same elution order as the Nucleodex β-PM column. Based on earlier reports, the atropisomers eluting first and second on the BGB-172 gas chromatography column are (aR)-(−)-PCB 84 and (aS)-(+)-PCB 84, respectively. -
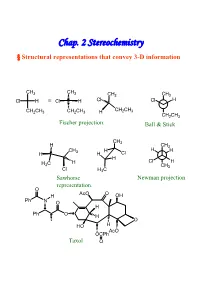
Chap. 2 Stereochemistry § Structural Representations That Convey 3-D Information
Chap. 2 Stereochemistry § Structural representations that convey 3-D information CH3 CH3 CH3 CH3 Cl H ≡ Cl H Cl Cl H CH CH CH2CH3 CH2CH3 H 2 3 CH2CH3 Fischer projection. Ball & Stick CH3 H CH3 CH H H H H 3 H Cl H H C H Cl H 3 CH3 Cl H3C Sawhorse Newman projection representation. O AcO O H OH Ph N O H Ph O H O HO H AcO OCPh Taxol O § Isomerism Isomers : Different compounds that have the same molecular formula. Conformational Isomer:Stereoisomers that are superimposable by rotation around a single bond. Enantiomer : Isomers that are non-superimposable mirror images to each other.→chiral Diastereomer:Isomers that are non-superimposable, not mirror images. -Cis-trans isomer ( geometric isomer ) configurational isomers differ around a double bond or cyclic structure. § Symmetric, Asymmetric, Dissymmetric and Nondissymmetric molecules. -Symmetry operation reflection in a plane(對稱面):σ inversion through a center(對稱中心):i rotation about a proper axis(對稱軸):Cn , for 360° /n rotation about an improper axis(更迭對稱軸):Sn ( = rotation about an axis, followed by reflection though a plane perpendicular to the axis ) H3C CH3 H CH3 C2, σv, σv’ C2, σh H H CH3 H H Cl2 H 2 Cl1 D1 i D2 F F F 1 F2 2 1 D2 D1 C2+σh=i =S Cl1 H H1 2 Cl2 C2 σh D2 F1 H2 Cl 2 Cl1 H1 F2 D1 XY XX X Ci Cs C2 YX X X X X X XXD X C2v C2h X 2h X D2d X X X Chirality:Molecules that are not superimposable with their mirror image chiral. -

Influence of the Chemical Environment on Metolachlor Conformations
J. Agric. Food Chem. 1999, 47, 4435−4442 4435 Influence of the Chemical Environment on Metolachlor Conformations Shalini Jayasundera,† Walter F. Schmidt,‡ Cathleen J. Hapeman,‡ and Alba Torrents*,† Department of Civil and Environmental Engineering, University of Maryland, College Park, Maryland 20742, and Environmental Chemistry Laboratory NRI, ARS/USDA, Beltsville, Maryland 20705 Metolachlor exists in multiple, different stable conformations in solution. Assignment of the NMR frequencies to chemical structure is a prerequisite to understanding the behavior of individual conformations. 1H NMR experiments of metolachlor in different chemical environments identified the labile sites of metolachlor and environments that influence conformational/configurational changes. Within very specific chemical environments, metolachlor atropisomers aS,12S (aR,12R) and aR,12S (aS,12R) freely interchange, and consequently, the multiple conformations also interchange. The changes in chemical environments, which most alter the conformations and molecular dynamics of metolachlor, identify the most critical components affecting its environmental fate. These results enable a structural interpretation of conformational changes that can influence the environmental fate of metolachlor. Keywords: Metolachlor; NMR; molecular mechanics; chemical environment; atropisomers INTRODUCTION gence herbicide used to control most annual grasses and The environmental fate of pesticides and other or- broad leaf weeds in beans, corn, cotton, potatoes, etc. ganic molecules depend on their interactions with the (Montgomery, 1993). It is one of the most widely used local chemical environment at the molecular level. Most pesticides in the U.S. agricultural crop production organic molecules are conformationally flexible, with the (Aspelin, 1994). In general, the chloroacetamides inhibit active conformations being only a few of the accessible the biosynthesis of fatty acids, lipids, proteins, iso- conformations in solution. -
D:\Data Files\Thèse\Rédaction\0
THÈSE Pour obtenir le diplôme de doctorat Spécialité Physique Préparée au sein de l’Université De Rouen Normandie Contribution to Chiral Discrimination in the Solid State & Access to Pure Enantiomer via Crystallization Présentée et soutenue par François-Xavier GENDRON Thèse soutenue publiquement le 29 Juin 2018 devant le jury composé de M. Richard M. KELLOGG Prof. University of Groningen Rapporteur M. Jean-Jacques COUNIOUX Prof. University of Lyon I Rapporteur Mme. Christine MARTIN Dr. University of Caen Examinateur M. Gérard COQUEREL Prof. University of Rouen Directeur de thèse Thèse dirigée par Gérard COQUEREL, professeur des universités au laboratoire Sciences et Méthodes Séparatives (EA 3233 SMS) A la pépite Agathe, arrivée au début de la fin. & A ma famille, qui m’a accompagné depuis 6 ans & A mon grand-père André, parti à la fin du début. “Don’t the great tales never end?” “No, they never end as tales,” said Frodo, “but the people in them come, and go when their part’s ended. Our part will end later – or sooner.” J. R. R. Tolkien, The Two Towers “If more of us valued food and cheer and song above hoarded gold, it would be a merrier world.” J. R. R Tolkien, The Hobbit Remerciements Remerciements Bien que cette thèse ait été rédigée dans la langue de Shakespeare, j’ai souhaité ici retourner à ma langue maternelle, celle de Molière, et ce afin de pouvoir pleinement y exprimer mes intentions. Mes tout premiers remerciements sont pour le Professeur Gérard Coquerel pour, le temps d’une pause lors d’un cours, avoir reçu, lu et finalement accepté ma demande de stage. -

Enantioselective Syntheses of Atropisomers Featuring a Five-Membered Ring Damien Bonne, Jean Rodriguez
Enantioselective syntheses of atropisomers featuring a five-membered ring Damien Bonne, Jean Rodriguez To cite this version: Damien Bonne, Jean Rodriguez. Enantioselective syntheses of atropisomers featuring a five-membered ring. Chemical Communications, Royal Society of Chemistry, 2017, 53 (92), pp.12385-12393. 10.1039/c7cc06863h. hal-01687197 HAL Id: hal-01687197 https://hal.archives-ouvertes.fr/hal-01687197 Submitted on 18 Jan 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. ChemComm FEATURE ARTICLE Enantioselective syntheses of atropisomers featuring a five-membered ring† Cite this: Chem. Commun., 2017, 53,12385 Damien Bonne * and Jean Rodriguez* Atropisomerism is a fundamental property of molecules featuring a hindered rotation around a chemical bond. If six-membered ring biaryl or heterobiaryl atropisomers are the most popular ones, the focus of Received 1st September 2017, Accepted 14th October 2017 this feature article will be put on less common and more challenging five-membered ring containing atropisomers displaying either a stereogenic C–N or C–C bond. After an historical background, DOI: 10.1039/c7cc06863h a description of the latest flourishing enantioselective strategies for the construction of this attractive family of atropisomers will be presented. -

Download Author Version (PDF)
Natural Product Reports A Twist of Nature – The Significance of Atropisomers in Biological Systems Journal: Natural Product Reports Manuscript ID: NP-REV-09-2014-000121.R2 Article Type: Review Article Date Submitted by the Author: 04-Aug-2015 Complete List of Authors: Smyth, Jamie; University of Wollongong, School of Chemistry Butler, Nicholas; University of Wollongong, School of Chemistry Keller, Paul; University of Wollongong, Chemistry Page 1 of 21 PleaseNatural do Product not adjust Reports margins NPR Review A Twist of Nature – The Significance of Atropisomers in Biological Systems Received 00th January 20xx, *† Accepted 00th January 20xx Jamie E. Smyth, Nicholas M. Butler, and Paul A. Keller DOI: 10.1039/x0xx00000x Recently identified natural atropisomeric compounds with potential medicinal applications are presented. The ability of natural receptors to possess differential binding between atropisomers is an important factor when considering active and www.rsc.org/ inactive atropisomeric drugs, and has required the development of new techniques for atropselective synthesis of desired targets. Advances in this field therefore have significant relevance to modern pharmaceutical and medicinal chemistry. The atropisomeric natural products discussed include hibarimicinone, flavomannins, talaromannins, viriditoxin, rugulotrosin A, abyssomicin C, marinopyrroles, dixiamycins, streptorubin B, ustiloxins A-F, haouamine A, bisnicalaterines, and tedarene B, all of which show significant potential as leads in antibiotic, antiviral and anticancer studies. The importance for the development of common practices regarding atropisomer recognition and classification is also emphasized. orientation for selective interaction with target proteins. While 1 Introduction this end is most commonly achieved by control of point chirality, there exists an under-appreciated form of isomerism, Natural products have long been a source of inspiration for which arises from conformational restriction; namely medicinal chemists, with a multitude of current atropisomerism.