DOCSLIB.ORG

The Transfer Function the Transfer Function

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Transfer Function the Transfer Function The Transfer Function The Transfer Function • A generalization of the frequency response • Taking the z-transforms of both sides we get function ∞ ∞ ∞ −n ⎛ ⎞ −n • The convolution sum description of an LTI Y(z) = ∑ y[n]z = ∑∑⎜ h[k]x[n − k]⎟ z discrete-time system with an impulse n=−∞ nk=−∞⎝ =−∞ ⎠ ∞ ∞ response h[n] is given by ⎛ −n ⎞ = ∑∑h[k]⎜ x[n − k]z ⎟ ∞ k=−∞ ⎝ n=−∞ ⎠ y[n] = ∑h[k]x[n − k] ∞ ⎛ ∞ ⎞ k=−∞ −(l+k) = ∑∑h[k]⎜ x[l]z ⎟ k=−∞ =−∞ 1 2 ⎝ l ⎠ Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra The Transfer Function The Transfer Function ∞ ⎛ ∞ ⎞ • Hence, −l −k •Or,Y(z) = ∑∑h[k]⎜ x[l]z ⎟ z H (z) = Y(z)/ X (z) k=−∞ ⎝ =−∞ ⎠ l • The function H(z), which is the z-transform of X (z) the impulse response h[n] of the LTI system, ⎛ ∞ ⎞ −k is called the transfer function or the system • Therefore, Y(z) = ⎜ ∑h[k]z ⎟ X (z) ⎝ k=−∞ ⎠ function H(z) • The inverse z-transform of the transfer function H(z) yields the impulse response h[n] • Thus, Y(z) = H(z)X(z) 3 4 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra The Transfer Function The Transfer Function • Consider an LTI discrete-time system characterized by a difference equation • Or, equivalently as M M −k ∑ pk z N d y[n − k] = M p x[n − k] H(z) = z(N −M ) k=0 ∑k=0 k ∑k=0 k N N −k ∑k=0 dk z • Its transfer function is obtained by taking • An alternate form of the transfer function is the z-transform of both sides of the above given by equation M −1 M −k p0 ∏k=1(1−ξk z ) ∑k=0 pk z H(z) = ⋅ • Thus H(z) = d N −1 N −k 0 ∏k=1(1− λk z ) ∑k=0 dk z 5 6 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra 1 The Transfer Function The Transfer Function • Or, equivalently as • For a causal IIR digital filter, the impulse M response is a causal sequence p ∏ (z −ξk ) H(z) = 0 z(N −M ) k=1 N • The ROC of the causal transfer function d0 (z − λ ) ∏k=1 k M p0 (N −M ) ∏k=1(z −ξk ) • ξ1, ξ2,...,ξM are the finite zeros, and H(z) = z d N λ1, λ2,...,λN are the finite poles of H(z) 0 ∏k=1(z − λk ) •IfN > M, there are additional ( N − M ) zeros is thus exterior to a circle going through the at z = 0 pole furthest from the origin •IfN < M, there are additional ( M − N ) poles • Thus the ROC is given by z > maxλk k at z = 0 7 8 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra The Transfer Function The Transfer Function • The transfer function has M zeros on the •Example- Consider the M-point moving- unit circle at z = e j 2 π k / M , 0 ≤ k ≤ M −1 average FIR filter with an impulse response • There are M − 1 poles at z = 0 and a single ⎧1/ M , 0 ≤ n ≤ M −1 pole at z = 1 M = 8 h[n] = ⎨ ⎩ 0, otherwise • The pole at z = 1 1 • Its transfer function is then given by exactly cancels the 0.5 7 0 M −1 −M M zero at z = 1 1 1− z z −1 Imaginary-0.5 Part H (z) z−n = = = ∑ −1 M • The ROC is the entire M n=0 M (1− z ) M[z (z −1)] -1 z-plane except z = 0 -1 -0.5 0 0.5 1 Real Part 9 10 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra The Transfer Function The Transfer Function • Alternate forms: z2 −1.2z +1 •Example- A causal LTI IIR digital filter is H (z) = described by a constant coefficient z3 −1.3z2 +1.04z − 0.222 difference equation given by (z − 0.6 + j0.8)(z − 0.6 − j0.8) = y[n] = x[n −1]−1.2 x[n − 2]+ x[n − 3]+1.3 y[n −1] (z − 0.3)(z − 0.5 + j0.7)(z − 0.5 − j0.7) 1 −1.04 y[n − 2]+ 0.222 y[n − 3] •Note:Poles farthest from 0.5 • Its transfer function is therefore given by z = 0 have a magnitude 0 z−1 −1.2z−2 + z−3 Imaginary-0.5 Part H (z) = 0.74 −1 −2 −3 -1 1−1.3z +1.04z − 0.222z -1 -0.5 0 0.5 1 11 12 • ROC: z > 0 . 74 Real Part Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra 2 Frequency Response from Frequency Response from Transfer Function Transfer Function • If the ROC of the transfer function H(z) • For a stable rational transfer function in the includes the unit circle, then the frequency form M H (e jω) p ∏ (z −ξk ) response of the LTI digital filter can H(z) = 0 z(N −M ) k=1 be obtained simply as follows: d N 0 ∏k=1(z − λk ) H (e jω) = H (z) z=e jω the factored form of the frequency response • For a real coefficient transfer function H(z) is given by it can be shown that M jω p ∏ (e − ξk ) jω 2 jω jω H (e jω) = 0 e jω(N −M ) k=1 H (e ) = H (e )H *(e ) d N jω jω − jω −1 0 ∏k=1(e − λk ) = H (e )H (e ) = H (z)H (z ) jω 13 z=e 14 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Frequency Response from Frequency Response from Transfer Function Transfer Function • It is convenient to visualize the contributions which reduces to M jω of the zero factor (z − ξ )and the pole factor p ∏ e − ξk k H (e jω) = 0 k=1 (z − λ ) from the factored form of the N jω k d0 e − λ frequency response ∏k=1 k • The phase response for a rational transfer • The magnitude function is given by function is of the form M jω p ∏ e − ξk jω H (e jω) = 0 e jω(N −M ) k=1 arg H (e ) = arg( p0 / d0) + ω(N − M ) d N jω M N 0 ∏k=1 e − λk jω jω + ∑arg(e − ξk ) − ∑arg(e − λk ) 15 16 k=1 k=1 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Frequency Response from Geometric Interpretation of Transfer Function Frequency Response Computation • The magnitude-squared function of a real- • The factored form of the frequency coefficient transfer function can be response M jω computed using p ∏ (e − ξk ) H (e jω) = 0 e jω(N −M ) k=1 N 2 M d jω jω − jω * 0 ∏k=1(e − λk ) jω 2 p0 ∏k=1(e − ξk )(e − ξk ) H (e ) = is convenient to develop a geometric d N (e jω − λ )(e− jω − λ* ) 0 ∏k=1 k k interpretation of the frequency response computation from the pole-zero plot as ω varies from 0 to 2π on the unit circle 17 18 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra 3 Geometric Interpretation of Geometric Interpretation of Frequency Response Computation Frequency Response Computation • The geometric interpretation can be used to • As shown below in the z-plane the factor obtain a sketch of the response as a function (e jω − ρe jφ) represents a vector starting at of the frequency the point z = ρ e jφ and ending on the unit jω • A typical factor in the factored form of the circle at z = e frequency response is given by (e jω − ρe jφ) where ρ e jφ is a zero if it is zero factor or is a pole if it is a pole factor 19 20 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Geometric Interpretation of Geometric Interpretation of Frequency Response Computation Frequency Response Computation •As ω is varied from 0 to 2π, the tip of the • As indicated by M jω vector moves counterclockise from the p ∏ e − ξk H (e jω) = 0 k=1 point z = 1 tracing the unit circle and back N jω d0 ∏ e − λk to the point z = 1 k=1 the magnitude response | H ( e j ω ) | at a specific value of ω is given by the product of the magnitudes of all zero vectors divided by the product of the magnitudes of all pole vectors 21 22 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Geometric Interpretation of Geometric Interpretation of Frequency Response Computation Frequency Response Computation • Likewise, from jω arg H (e ) = arg( p0 / d0) + ω(N − M ) • Thus, an approximate plot of the magnitude + ∑M arg(e jω − ξ ) − ∑N arg(e jω − λ ) and phase responses of the transfer function k=1 k k=1 k of an LTI digital filter can be developed by we observe that the phase response examining the pole and zero locations at a specific value of ω is obtained by • Now, a zero (pole) vector has the smallest adding the phase of the term p / d and the 0 0 magnitude when ω = φ linear-phase term ω ( N − M ) to the sum of the angles of the zero vectors minus the angles of the pole vectors 23 24 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra 4 Geometric Interpretation of Stability Condition in Terms of Frequency Response Computation Frequency Response Computation the Pole Locations • To highly attenuate signal components in a • A causal LTI digital filter is BIBO stable if specified frequency range, we need to place and only if its impulse response h[n] is zeros very close to or on the unit circle in absolutely summable, i.e., this range ∞ • Likewise, to highly emphasize signal S = ∑ h[n] < ∞ components in a specified frequency range, n=−∞ we need to place poles very close to or on • We now develop a stability condition in the unit circle in this range terms of the pole locations of the transfer function H(z) 25 26 Copyright © 2005, S.
Load more

Recommended publications
  • Lecture 3: Transfer Function and Dynamic Response Analysis
    Transfer function approach Dynamic response Summary Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis Paweł Malczyk Division of Theory of Machines and Robots Institute of Aeronautics and Applied Mechanics Faculty of Power and Aeronautical Engineering Warsaw University of Technology October 17, 2019 © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 1 / 31 Transfer function approach Dynamic response Summary Outline 1 Transfer function approach 2 Dynamic response 3 Summary © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 2 / 31 Transfer function approach Dynamic response Summary Transfer function approach 1 Transfer function approach SISO system Definition Poles and zeros Transfer function for multivariable system Properties 2 Dynamic response 3 Summary © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 3 / 31 Transfer function approach Dynamic response Summary SISO system Fig. 1: Block diagram of a single input single output (SISO) system Consider the continuous, linear time-invariant (LTI) system defined by linear constant coefficient ordinary differential equation (LCCODE): dny dn−1y + − + ··· + _ + = an n an 1 n−1 a1y a0y dt dt (1) dmu dm−1u = b + b − + ··· + b u_ + b u m dtm m 1 dtm−1 1 0 initial conditions y(0), y_(0),..., y(n−1)(0), and u(0),..., u(m−1)(0) given, u(t) – input signal, y(t) – output signal, ai – real constants for i = 1, ··· , n, and bj – real constants for j = 1, ··· , m. How do I find the LCCODE (1)? .
    [Show full text]
  • Control Theory
    Control theory S. Simrock DESY, Hamburg, Germany Abstract In engineering and mathematics, control theory deals with the behaviour of dynamical systems. The desired output of a system is called the reference. When one or more output variables of a system need to follow a certain ref- erence over time, a controller manipulates the inputs to a system to obtain the desired effect on the output of the system. Rapid advances in digital system technology have radically altered the control design options. It has become routinely practicable to design very complicated digital controllers and to carry out the extensive calculations required for their design. These advances in im- plementation and design capability can be obtained at low cost because of the widespread availability of inexpensive and powerful digital processing plat- forms and high-speed analog IO devices. 1 Introduction The emphasis of this tutorial on control theory is on the design of digital controls to achieve good dy- namic response and small errors while using signals that are sampled in time and quantized in amplitude. Both transform (classical control) and state-space (modern control) methods are described and applied to illustrative examples. The transform methods emphasized are the root-locus method of Evans and fre- quency response. The state-space methods developed are the technique of pole assignment augmented by an estimator (observer) and optimal quadratic-loss control. The optimal control problems use the steady-state constant gain solution. Other topics covered are system identification and non-linear control. System identification is a general term to describe mathematical tools and algorithms that build dynamical models from measured data.
    [Show full text]
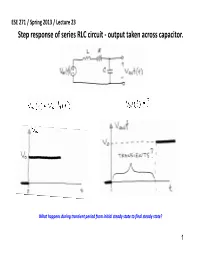
  • Step Response of Series RLC Circuit ‐ Output Taken Across Capacitor
    ESE 271 / Spring 2013 / Lecture 23 Step response of series RLC circuit ‐ output taken across capacitor. What happens during transient period from initial steady state to final steady state? 1 ESE 271 / Spring 2013 / Lecture 23 Transfer function of series RLC ‐ output taken across capacitor. Poles: Case 1: ‐‐two differen t real poles Case 2: ‐ two identical real poles ‐ complex conjugate poles Case 3: 2 ESE 271 / Spring 2013 / Lecture 23 Case 1: two different real poles. Step response of series RLC ‐ output taken across capacitor. Overdamped case –the circuit demonstrates relatively slow transient response. 3 ESE 271 / Spring 2013 / Lecture 23 Case 1: two different real poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Uncorrected Bode Gain Plot Overdamped case –the circuit demonstrates relatively limited bandwidth 4 ESE 271 / Spring 2013 / Lecture 23 Case 2: two identical real poles. Step response of series RLC ‐ output taken across capacitor. Critically damped case –the circuit demonstrates the shortest possible rise time without overshoot. 5 ESE 271 / Spring 2013 / Lecture 23 Case 2: two identical real poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Critically damped case –the circuit demonstrates the widest bandwidth without apparent resonance. Uncorrected Bode Gain Plot 6 ESE 271 / Spring 2013 / Lecture 23 Case 3: two complex poles. Step response of series RLC ‐ output taken across capacitor. Underdamped case – the circuit oscillates. 7 ESE 271 / Spring 2013 / Lecture 23 Case 3: two complex poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Corrected Bode GiGain Plot Underdamped case –the circuit can demonstrate apparent resonant behavior.
    [Show full text]
  • Frequency Response and Bode Plots
    1 Frequency Response and Bode Plots 1.1 Preliminaries The steady-state sinusoidal frequency-response of a circuit is described by the phasor transfer function Hj( ) . A Bode plot is a graph of the magnitude (in dB) or phase of the transfer function versus frequency. Of course we can easily program the transfer function into a computer to make such plots, and for very complicated transfer functions this may be our only recourse. But in many cases the key features of the plot can be quickly sketched by hand using some simple rules that identify the impact of the poles and zeroes in shaping the frequency response. The advantage of this approach is the insight it provides on how the circuit elements influence the frequency response. This is especially important in the design of frequency-selective circuits. We will first consider how to generate Bode plots for simple poles, and then discuss how to handle the general second-order response. Before doing this, however, it may be helpful to review some properties of transfer functions, the decibel scale, and properties of the log function. Poles, Zeroes, and Stability The s-domain transfer function is always a rational polynomial function of the form Ns() smm as12 a s m asa Hs() K K mm12 10 (1.1) nn12 n Ds() s bsnn12 b s bsb 10 As we have seen already, the polynomials in the numerator and denominator are factored to find the poles and zeroes; these are the values of s that make the numerator or denominator zero. If we write the zeroes as zz123,, zetc., and similarly write the poles as pp123,, p , then Hs( ) can be written in factored form as ()()()s zsz sz Hs() K 12 m (1.2) ()()()s psp12 sp n 1 © Bob York 2009 2 Frequency Response and Bode Plots The pole and zero locations can be real or complex.
    [Show full text]
  • Linear Time Invariant Systems
    UNIT III LINEAR TIME INVARIANT CONTINUOUS TIME SYSTEMS CT systems – Linear Time invariant Systems – Basic properties of continuous time systems – Linearity, Causality, Time invariance, Stability – Frequency response of LTI systems – Analysis and characterization of LTI systems using Laplace transform – Computation of impulse response and transfer function using Laplace transform – Differential equation – Impulse response – Convolution integral and Frequency response. System A system may be defined as a set of elements or functional blocks which are connected together and produces an output in response to an input signal. The response or output of the system depends upon transfer function of the system. Mathematically, the functional relationship between input and output may be written as y(t)=f[x(t)] Types of system Like signals, systems may also be of two types as under: 1. Continuous-time system 2. Discrete time system Continuous time System Continuous time system may be defined as those systems in which the associated signals are also continuous. This means that input and output of continuous – time system are both continuous time signals. For example: Audio, video amplifiers, power supplies etc., are continuous time systems. Discrete time systems Discrete time system may be defined as a system in which the associated signals are also discrete time signals. This means that in a discrete time system, the input and output are both discrete time signals. For example, microprocessors, semiconductor memories, shift registers etc., are discrete time signals. LTI system:- Systems are broadly classified as continuous time systems and discrete time systems. Continuous time systems deal with continuous time signals and discrete time systems deal with discrete time system.
    [Show full text]
  • Simplified, Physically-Informed Models of Distortion and Overdrive Guitar Effects Pedals
    Proc. of the 10th Int. Conference on Digital Audio Effects (DAFx-07), Bordeaux, France, September 10-15, 2007 SIMPLIFIED, PHYSICALLY-INFORMED MODELS OF DISTORTION AND OVERDRIVE GUITAR EFFECTS PEDALS David T. Yeh, Jonathan S. Abel and Julius O. Smith Center for Computer Research in Music and Acoustics (CCRMA) Stanford University, Stanford, CA [dtyeh|abel|jos]@ccrma.stanford.edu ABSTRACT retained, however, because intermodulation due to mixing of sub- sonic components with audio frequency components is noticeable This paper explores a computationally efficient, physically in- in the audio band. formed approach to design algorithms for emulating guitar distor- tion circuits. Two iconic effects pedals are studied: the “Distor- Stages are partitioned at points in the circuit where an active tion” pedal and the “Tube Screamer” or “Overdrive” pedal. The element with low source impedance drives a high impedance load. primary distortion mechanism in both pedals is a diode clipper This approximation is also made with less accuracy where passive with an embedded low-pass filter, and is shown to follow a non- components feed into loads with higher impedance. Neglecting linear ordinary differential equation whose solution is computa- the interaction between the stages introduces magnitude error by a tionally expensive for real-time use. In the proposed method, a scalar factor and neglects higher order terms in the transfer func- simplified model, comprising the cascade of a conditioning filter, tion that are usually small in the audio band. memoryless nonlinearity and equalization filter, is chosen for its The nonlinearity may be evaluated as a nonlinear ordinary dif- computationally efficient, numerically robust properties.
    [Show full text]
  • Control System Design Methods
    Christiansen-Sec.19.qxd 06:08:2004 6:43 PM Page 19.1 The Electronics Engineers' Handbook, 5th Edition McGraw-Hill, Section 19, pp. 19.1-19.30, 2005. SECTION 19 CONTROL SYSTEMS Control is used to modify the behavior of a system so it behaves in a specific desirable way over time. For example, we may want the speed of a car on the highway to remain as close as possible to 60 miles per hour in spite of possible hills or adverse wind; or we may want an aircraft to follow a desired altitude, heading, and velocity profile independent of wind gusts; or we may want the temperature and pressure in a reactor vessel in a chemical process plant to be maintained at desired levels. All these are being accomplished today by control methods and the above are examples of what automatic control systems are designed to do, without human intervention. Control is used whenever quantities such as speed, altitude, temperature, or voltage must be made to behave in some desirable way over time. This section provides an introduction to control system design methods. P.A., Z.G. In This Section: CHAPTER 19.1 CONTROL SYSTEM DESIGN 19.3 INTRODUCTION 19.3 Proportional-Integral-Derivative Control 19.3 The Role of Control Theory 19.4 MATHEMATICAL DESCRIPTIONS 19.4 Linear Differential Equations 19.4 State Variable Descriptions 19.5 Transfer Functions 19.7 Frequency Response 19.9 ANALYSIS OF DYNAMICAL BEHAVIOR 19.10 System Response, Modes and Stability 19.10 Response of First and Second Order Systems 19.11 Transient Response Performance Specifications for a Second Order
    [Show full text]
  • Mathematical Modeling of Control Systems
    OGATA-CH02-013-062hr 7/14/09 1:51 PM Page 13 2 Mathematical Modeling of Control Systems 2–1 INTRODUCTION In studying control systems the reader must be able to model dynamic systems in math- ematical terms and analyze their dynamic characteristics.A mathematical model of a dy- namic system is defined as a set of equations that represents the dynamics of the system accurately, or at least fairly well. Note that a mathematical model is not unique to a given system.A system may be represented in many different ways and, therefore, may have many mathematical models, depending on one’s perspective. The dynamics of many systems, whether they are mechanical, electrical, thermal, economic, biological, and so on, may be described in terms of differential equations. Such differential equations may be obtained by using physical laws governing a partic- ular system—for example, Newton’s laws for mechanical systems and Kirchhoff’s laws for electrical systems. We must always keep in mind that deriving reasonable mathe- matical models is the most important part of the entire analysis of control systems. Throughout this book we assume that the principle of causality applies to the systems considered.This means that the current output of the system (the output at time t=0) depends on the past input (the input for t<0) but does not depend on the future input (the input for t>0). Mathematical Models. Mathematical models may assume many different forms. Depending on the particular system and the particular circumstances, one mathemati- cal model may be better suited than other models.
    [Show full text]
  • 12: Resonance
    12: Resonance • QuadraticFactors + • Damping Factor and Q • Parallel RLC • Behaviour at Resonance • Away from resonance • Bandwidth and Q • Power and Energy at Resonance + • Low Pass Filter • Resonance Peak for LP filter • Summary 12: Resonance E1.1 Analysis of Circuits (2017-10213) Resonance: 12 – 1 / 11 Quadratic Factors + 12: Resonance 2 • QuadraticFactors + A quadratic factor in a transfer function is: F (jω) = a (jω) + b (jω) + c. • Damping Factor and Q • Parallel RLC • Behaviour at Resonance • Away from resonance • Bandwidth and Q • Power and Energy at Resonance + • Low Pass Filter • Resonance Peak for LP filter • Summary E1.1 Analysis of Circuits (2017-10213) Resonance: 12 – 2 / 11 Quadratic Factors + 12: Resonance 2 • QuadraticFactors + A quadratic factor in a transfer function is: F (jω) = a (jω) + b (jω) + c. • Damping Factor and Q • Parallel RLC 2 • Behaviour at Resonance Case 1: If b 4ac then we can factorize it: • Away from resonance ≥ • Bandwidth and Q F (jω) = a(jω p1)(jω p2) • Power and Energy at − − Resonance + • Low Pass Filter • Resonance Peak for LP filter • Summary E1.1 Analysis of Circuits (2017-10213) Resonance: 12 – 2 / 11 Quadratic Factors + 12: Resonance 2 • QuadraticFactors + A quadratic factor in a transfer function is: F (jω) = a (jω) + b (jω) + c. • Damping Factor and Q • Parallel RLC 2 • Behaviour at Resonance Case 1: If b 4ac then we can factorize it: • Away from resonance ≥ • Bandwidth and Q F (jω) = a(jω p1)(jω p2) • Power and Energy at − − Resonance + b √b2 4ac • Low Pass Filter where p = − ± − . • Resonance Peak for LP i 2a filter • Summary E1.1 Analysis of Circuits (2017-10213) Resonance: 12 – 2 / 11 Quadratic Factors ++ 12: Resonance 2 • QuadraticFactors + A quadratic factor in a transfer function is: F (jω) = a (jω) + b (jω) + c.
    [Show full text]
  • Discussion 3B
    EECS 16B Designing Information Devices and Systems II Spring 2018 J. Roychowdhury and M. Maharbiz Discussion 3B 1 Transfer Functions When we analyzed circuits in the phasor domain, we always told you what the input voltage, or the input sinusoid to the circuit was. However, sometimes we have many input sinusoids, and we want to look at how a circuit (or system) generically responds to a sinusoid input of frequency w. We want to see how an input sinusoid “transfers” into an output sinusoid. How do we do this? Let’s start with a simple RC circuit. R i(t) + + vin C vout − − Figure 1: First Order RC Low Pass Filter 1 In the phasor domain, the impedance of the capacitor is ZC = jwC and the impedance of the resistor is ZR = R. Because we treat impedances the same as resistances, this circuit looks like a voltage divider in the phasor domain. Remember we must also represent vin as a phasor V˜in; transfer functions are in the phasor domain only, not the time domain. 1 Z 1 V˜ = C V˜ = jwC V˜ = V˜ out Z + Z in 1 in jwRC + 1 in R C R + jwC We define the frequency response as V˜ 1 H(w) = out = V˜in jwRC + 1 Now, given an arbitrary input sinusoid, if we multiply it by the frequency response, we can get the output sinusoid. What this allows us to do is to model any arbitrary circuit as a 4-port (two input, two output) black box. The transfer function completely defines how our circuit works.
    [Show full text]
  • Resonance of Fractional Transfer Functions of the Second Kind Rachid Malti, Xavier Moreau, Firas Khemane
    Resonance of fractional transfer functions of the second kind Rachid Malti, Xavier Moreau, Firas Khemane To cite this version: Rachid Malti, Xavier Moreau, Firas Khemane. Resonance of fractional transfer functions of the second kind. The 3th IFAC Workshop on Fractional Differentiation and its Applications, FDA08, Nov 2008, Ankara, Turkey. pp.1-6. hal-00326418 HAL Id: hal-00326418 https://hal.archives-ouvertes.fr/hal-00326418 Submitted on 26 Jan 2009 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Resonance of fractional transfer functions of the second kind Rachid MALTI, Xavier MOREAU, and Firas KHEMANE ∗ Bordeaux University – IMS, 351, cours de la Lib´eration, 33405 Talence Cedex, France. firstname.lastname @ims-bordeaux.fr { } Abstract: Canonical fractional transfer function of the second kind is studied in this paper. Stability and resonance conditions are determined in terms of pseudo-damping factor and commensurable order. Keywords: Resonance, fractional system, second order transfer function, canonical form. 1. INTRODUCTION F (s) + + 1 1 Σ K1 ν Σ K2 Commensurable fractional systems can be represented in s sν a transfer function form as: mB − − b sνj ν j T (s ) j=0 H (s)= = , (1) ν PmA R(s ) νi 1+ ais Fig.
    [Show full text]
  • The Z-Transform
    CHAPTER 33 The z-Transform Just as analog filters are designed using the Laplace transform, recursive digital filters are developed with a parallel technique called the z-transform. The overall strategy of these two transforms is the same: probe the impulse response with sinusoids and exponentials to find the system's poles and zeros. The Laplace transform deals with differential equations, the s-domain, and the s-plane. Correspondingly, the z-transform deals with difference equations, the z-domain, and the z-plane. However, the two techniques are not a mirror image of each other; the s-plane is arranged in a rectangular coordinate system, while the z-plane uses a polar format. Recursive digital filters are often designed by starting with one of the classic analog filters, such as the Butterworth, Chebyshev, or elliptic. A series of mathematical conversions are then used to obtain the desired digital filter. The z-transform provides the framework for this mathematics. The Chebyshev filter design program presented in Chapter 20 uses this approach, and is discussed in detail in this chapter. The Nature of the z-Domain To reinforce that the Laplace and z-transforms are parallel techniques, we will start with the Laplace transform and show how it can be changed into the z- transform. From the last chapter, the Laplace transform is defined by the relationship between the time domain and s-domain signals: 4 X(s) ' x(t) e &st dt m t '&4 where x(t) and X(s) are the time domain and s-domain representation of the signal, respectively.
    [Show full text]