Frequency Response and Bode Plots
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lesson 22: Determining Control Stability Using Bode Plots
11/30/2015 Lesson 22: Determining Control Stability Using Bode Plots 1 ET 438A AUTOMATIC CONTROL SYSTEMS TECHNOLOGY lesson22et438a.pptx Learning Objectives 2 After this presentation you will be able to: List the control stability criteria for open loop frequency response. Identify the gain and phase margins necessary for a stable control system. Use a Bode plot to determine if a control system is stable or unstable. Generate Bode plots of control systems the include dead-time delay and determine system stability. lesson22et438a.pptx 1 11/30/2015 Bode Plot Stability Criteria 3 Open loop gain of less than 1 (G<1 or G<0dB) at Stable Control open loop phase angle of -180 degrees System Oscillatory Open loop gain of exactly 1 (G=1 or G= 0dB) at Control System open loop phase angle of -180 degrees Marginally Stable Unstable Control Open loop gain of greater than 1 (G>1 or G>0dB) System at open loop phase angle of -180 degrees lesson22et438a.pptx Phase and Gain Margins 4 Inherent error and inaccuracies require ranges of phase shift and gain to insure stability. Gain Margin – Safe level below 1 required for stability Minimum level : G=0.5 or -6 dB at phase shift of 180 degrees Phase Margin – Safe level above -180 degrees required for stability Minimum level : f=40 degree or -180+ 40=-140 degrees at gain level of 0.5 or 0 dB. lesson22et438a.pptx 2 11/30/2015 Determining Phase and Gain Margins 5 Define two frequencies: wodB = frequency of 0 dB gain w180 = frequency of -180 degree phase shift Open Loop Gain 0 dB Gain Margin -m180 bodB Phase Margin -180+b0dB -180o Open Loop w w Phase odB 180 lesson22et438a.pptx Determining Phase and Gain Margins 6 Procedure: 1) Draw vertical lines through 0 dB on gain and -180 on phase plots. -

RANDOM VIBRATION—AN OVERVIEW by Barry Controls, Hopkinton, MA
RANDOM VIBRATION—AN OVERVIEW by Barry Controls, Hopkinton, MA ABSTRACT Random vibration is becoming increasingly recognized as the most realistic method of simulating the dynamic environment of military applications. Whereas the use of random vibration specifications was previously limited to particular missile applications, its use has been extended to areas in which sinusoidal vibration has historically predominated, including propeller driven aircraft and even moderate shipboard environments. These changes have evolved from the growing awareness that random motion is the rule, rather than the exception, and from advances in electronics which improve our ability to measure and duplicate complex dynamic environments. The purpose of this article is to present some fundamental concepts of random vibration which should be understood when designing a structure or an isolation system. INTRODUCTION Random vibration is somewhat of a misnomer. If the generally accepted meaning of the term "random" were applicable, it would not be possible to analyze a system subjected to "random" vibration. Furthermore, if this term were considered in the context of having no specific pattern (i.e., haphazard), it would not be possible to define a vibration environment, for the environment would vary in a totally unpredictable manner. Fortunately, this is not the case. The majority of random processes fall in a special category termed stationary. This means that the parameters by which random vibration is characterized do not change significantly when analyzed statistically over a given period of time - the RMS amplitude is constant with time. For instance, the vibration generated by a particular event, say, a missile launch, will be statistically similar whether the event is measured today or six months from today. -

EE C128 Chapter 10
Lecture abstract EE C128 / ME C134 – Feedback Control Systems Topics covered in this presentation Lecture – Chapter 10 – Frequency Response Techniques I Advantages of FR techniques over RL I Define FR Alexandre Bayen I Define Bode & Nyquist plots I Relation between poles & zeros to Bode plots (slope, etc.) Department of Electrical Engineering & Computer Science st nd University of California Berkeley I Features of 1 -&2 -order system Bode plots I Define Nyquist criterion I Method of dealing with OL poles & zeros on imaginary axis I Simple method of dealing with OL stable & unstable systems I Determining gain & phase margins from Bode & Nyquist plots I Define static error constants September 10, 2013 I Determining static error constants from Bode & Nyquist plots I Determining TF from experimental FR data Bayen (EECS, UCB) Feedback Control Systems September 10, 2013 1 / 64 Bayen (EECS, UCB) Feedback Control Systems September 10, 2013 2 / 64 10 FR techniques 10.1 Intro Chapter outline 1 10 Frequency response techniques 1 10 Frequency response techniques 10.1 Introduction 10.1 Introduction 10.2 Asymptotic approximations: Bode plots 10.2 Asymptotic approximations: Bode plots 10.3 Introduction to Nyquist criterion 10.3 Introduction to Nyquist criterion 10.4 Sketching the Nyquist diagram 10.4 Sketching the Nyquist diagram 10.5 Stability via the Nyquist diagram 10.5 Stability via the Nyquist diagram 10.6 Gain margin and phase margin via the Nyquist diagram 10.6 Gain margin and phase margin via the Nyquist diagram 10.7 Stability, gain margin, and -

Lecture 3: Transfer Function and Dynamic Response Analysis
Transfer function approach Dynamic response Summary Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis Paweł Malczyk Division of Theory of Machines and Robots Institute of Aeronautics and Applied Mechanics Faculty of Power and Aeronautical Engineering Warsaw University of Technology October 17, 2019 © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 1 / 31 Transfer function approach Dynamic response Summary Outline 1 Transfer function approach 2 Dynamic response 3 Summary © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 2 / 31 Transfer function approach Dynamic response Summary Transfer function approach 1 Transfer function approach SISO system Definition Poles and zeros Transfer function for multivariable system Properties 2 Dynamic response 3 Summary © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 3 / 31 Transfer function approach Dynamic response Summary SISO system Fig. 1: Block diagram of a single input single output (SISO) system Consider the continuous, linear time-invariant (LTI) system defined by linear constant coefficient ordinary differential equation (LCCODE): dny dn−1y + − + ··· + _ + = an n an 1 n−1 a1y a0y dt dt (1) dmu dm−1u = b + b − + ··· + b u_ + b u m dtm m 1 dtm−1 1 0 initial conditions y(0), y_(0),..., y(n−1)(0), and u(0),..., u(m−1)(0) given, u(t) – input signal, y(t) – output signal, ai – real constants for i = 1, ··· , n, and bj – real constants for j = 1, ··· , m. How do I find the LCCODE (1)? . -

I Introduction and Background
Final Design Report Platform Motion Measurement System ELEC 492 A Senior Design Project, 2005 Between University of San Diego And Trex Enterprises Submitted to: Dr. Lord at USD Prepared by: YAZ Zlatko Filipovic Yoshitaka Yano August 12, 2005 University of San Diego Final Design Report USD August 12, 2005 Platform Motion Measurement System Table of Contents I. Acknowledgments…………...…………………………………………………………4 II. Executive Summary……..…………………………………………………………….5 III. Introduction and Background…...………………………...………………………….6 IV. Project Requirements…………….................................................................................8 V. Methodology of Design Plan……….…..……………..…….………….…..…….…..11 VI. Testing….……………………………………..…..…………………….……...........21 VII. Deliverables and Project Results………...…………...…………..…….…………...24 VIII. Budget………………………………………...……..……………………………..25 IX. Personnel…………………..………………………………………....….……….......28 X. Design Schedule………….…...……………………………….……...…………........29 XI. Reference and Bibliography…………..…………..…………………...…………….31 XII. Summary…………………………………………………………………………....32 Appendices Appendix 1. Simulink Simulations…..………………………….…….33 Appendix 2. VisSim Simulations..........……………………………….34 Appendix 3. Frequency Response and VisSim results……………......36 Appendix 4. Vibration Measurements…………..………………….….38 Appendix 5. PCB Layout and Schematic……………………………..39 Appendix 6. User’s Manual…………………………………………..41 Appendix 7. PSpice Simulations of Hfilter…………………………….46 1 Final Design Report USD August 12, 2005 Platform Motion Measurement System -

Amplifier Frequency Response
EE105 – Fall 2015 Microelectronic Devices and Circuits Prof. Ming C. Wu [email protected] 511 Sutardja Dai Hall (SDH) 2-1 Amplifier Gain vO Voltage Gain: Av = vI iO Current Gain: Ai = iI load power vOiO Power Gain: Ap = = input power vIiI Note: Ap = Av Ai Note: Av and Ai can be positive, negative, or even complex numbers. Nagative gain means the output is 180° out of phase with input. However, power gain should always be a positive number. Gain is usually expressed in Decibel (dB): 2 Av (dB) =10log Av = 20log Av 2 Ai (dB) =10log Ai = 20log Ai Ap (dB) =10log Ap 2-2 1 Amplifier Power Supply and Dissipation • Circuit needs dc power supplies (e.g., battery) to function. • Typical power supplies are designated VCC (more positive voltage supply) and -VEE (more negative supply). • Total dc power dissipation of the amplifier Pdc = VCC ICC +VEE IEE • Power balance equation Pdc + PI = PL + Pdissipated PI : power drawn from signal source PL : power delivered to the load (useful power) Pdissipated : power dissipated in the amplifier circuit (not counting load) P • Amplifier power efficiency η = L Pdc Power efficiency is important for "power amplifiers" such as output amplifiers for speakers or wireless transmitters. 2-3 Amplifier Saturation • Amplifier transfer characteristics is linear only over a limited range of input and output voltages • Beyond linear range, the output voltage (or current) waveforms saturates, resulting in distortions – Lose fidelity in stereo – Cause interference in wireless system 2-4 2 Symbol Convention iC (t) = IC +ic (t) iC (t) : total instantaneous current IC : dc current ic (t) : small signal current Usually ic (t) = Ic sinωt Please note case of the symbol: lowercase-uppercase: total current lowercase-lowercase: small signal ac component uppercase-uppercase: dc component uppercase-lowercase: amplitude of ac component Similarly for voltage expressions. -

Meeting Design Specifications
NDSU Meeting Design Specs using Bode Plots ECE 461 Meeting Design Specs using Bode Plots When designing a compensator to meet design specs including: Steady-state error for a step input Phase Margin 0dB gain frequency the procedure using Bode plots is about the same as it was for root-locus plots. Add a pole at s = 0 if needed (making the system type-1) Start cancelling zeros until the system is too fast For every zero you added, add a pole. Place these poles so that the phase adds up. When using root-locus techniques, the phase adds up to 180 degrees at some spot on the s-plane. When using Bode plot techniques, the phase adds up to give you your phase margin at some spot on the jw axis. Example 1: Problem: Given the following system 1000 G(s) = (s+1)(s+3)(s+6)(s+10) Design a compensator which result in No error for a step input 20% overshoot for a step input, and A settling time of 4 second Solution: First, convert to Bode Plot terminology No overshoot means make this a type-1 system. Add a pole at s = 0. 20% overshoot means ζ = 0.4559 Mm = 1.2322 GK = 1∠ − 132.120 Phase Margin = 47.88 degrees A settling time of 4 seconds means s = -1 + j X s = -1 + j2 (from the damping ratio) The 0dB gain frequency is 2.00 rad/sec In short, design K(s) so that the system is type-1 and 0 (GK)s=j2 = 1∠ − 132.12 JSG 1 rev June 22, 2016 NDSU Meeting Design Specs using Bode Plots ECE 461 Start with s+1 K(s) = s At 4 rad/sec 1000 0 GK = s(s+3)(s+6)(s+10) = 2.1508∠ − 153.43 s=j2 There is too much phase shift, so start cancelling zeros. -

Control Theory
Control theory S. Simrock DESY, Hamburg, Germany Abstract In engineering and mathematics, control theory deals with the behaviour of dynamical systems. The desired output of a system is called the reference. When one or more output variables of a system need to follow a certain ref- erence over time, a controller manipulates the inputs to a system to obtain the desired effect on the output of the system. Rapid advances in digital system technology have radically altered the control design options. It has become routinely practicable to design very complicated digital controllers and to carry out the extensive calculations required for their design. These advances in im- plementation and design capability can be obtained at low cost because of the widespread availability of inexpensive and powerful digital processing plat- forms and high-speed analog IO devices. 1 Introduction The emphasis of this tutorial on control theory is on the design of digital controls to achieve good dy- namic response and small errors while using signals that are sampled in time and quantized in amplitude. Both transform (classical control) and state-space (modern control) methods are described and applied to illustrative examples. The transform methods emphasized are the root-locus method of Evans and fre- quency response. The state-space methods developed are the technique of pole assignment augmented by an estimator (observer) and optimal quadratic-loss control. The optimal control problems use the steady-state constant gain solution. Other topics covered are system identification and non-linear control. System identification is a general term to describe mathematical tools and algorithms that build dynamical models from measured data. -

Applications Academic Program Distributing Vissim Models
VISSIM VisSim is a visual block diagram language for simulation of dynamical systems and Model Based Design of embedded systems. It is developed by Visual Solutions of Westford, Massachusetts. Applications VisSim is widely used in control system design and digital signal processing for multidomain simulation and design. It includes blocks for arithmetic, Boolean, and transcendental functions, as well as digital filters, transfer functions, numerical integration and interactive plotting. The most commonly modeled systems are aeronautical, biological/medical, digital power, electric motor, electrical, hydraulic, mechanical, process, thermal/HVAC and econometric. Academic program The VisSim Free Academic Program allows accredited educational institutions to site license VisSim v3.0 for no cost. The latest versions of VisSim and addons are also available to students and academic institutions at greatly reduced pricing. Distributing VisSim models VisSim viewer screenshot with sample model. The free Vis Sim Viewer is a convenient way to share VisSim models with colleagues and clients not licensed to use VisSim. The VisSim Viewer will execute any VisSim model, and allows changes to block and simulation parameters to illustrate different design scenarios. Sliders and buttons may be activated if included in the model. Code generation The VisSim/C-Code add-on generates efficient, readable ANSI C code for algorithm acceleration and real-time implementation of embedded systems. The code is more efficient and readable than most other code generators. VisSim's author served on the X3J11 ANSI C committee and wrote several C compilers, in addition to co-authoring a book on C. [2] This deep understanding of ANSI C, and the nature of the resulting machine code when compiled, is the key to the code generator's efficiency. -
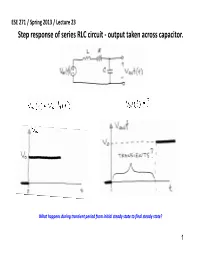
Step Response of Series RLC Circuit ‐ Output Taken Across Capacitor
ESE 271 / Spring 2013 / Lecture 23 Step response of series RLC circuit ‐ output taken across capacitor. What happens during transient period from initial steady state to final steady state? 1 ESE 271 / Spring 2013 / Lecture 23 Transfer function of series RLC ‐ output taken across capacitor. Poles: Case 1: ‐‐two differen t real poles Case 2: ‐ two identical real poles ‐ complex conjugate poles Case 3: 2 ESE 271 / Spring 2013 / Lecture 23 Case 1: two different real poles. Step response of series RLC ‐ output taken across capacitor. Overdamped case –the circuit demonstrates relatively slow transient response. 3 ESE 271 / Spring 2013 / Lecture 23 Case 1: two different real poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Uncorrected Bode Gain Plot Overdamped case –the circuit demonstrates relatively limited bandwidth 4 ESE 271 / Spring 2013 / Lecture 23 Case 2: two identical real poles. Step response of series RLC ‐ output taken across capacitor. Critically damped case –the circuit demonstrates the shortest possible rise time without overshoot. 5 ESE 271 / Spring 2013 / Lecture 23 Case 2: two identical real poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Critically damped case –the circuit demonstrates the widest bandwidth without apparent resonance. Uncorrected Bode Gain Plot 6 ESE 271 / Spring 2013 / Lecture 23 Case 3: two complex poles. Step response of series RLC ‐ output taken across capacitor. Underdamped case – the circuit oscillates. 7 ESE 271 / Spring 2013 / Lecture 23 Case 3: two complex poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Corrected Bode GiGain Plot Underdamped case –the circuit can demonstrate apparent resonant behavior. -

Evaluation of Audio Test Methods and Measurements for End-Of-Line Loudspeaker Quality Control
Evaluation of audio test methods and measurements for end-of-line loudspeaker quality control Steve Temme1 and Viktor Dobos2 (1. Listen, Inc., Boston, MA, 02118, USA. [email protected]; 2. Harman/Becker Automotive Systems Kft., H-8000 Székesfehérvár, Hungary) ABSTRACT In order to minimize costly warranty repairs, loudspeaker OEMS impose tight specifications and a “total quality” requirement on their part suppliers. At the same time, they also require low prices. This makes it important for driver manufacturers and contract manufacturers to work with their OEM customers to define reasonable specifications and tolerances. They must understand both how the loudspeaker OEMS are testing as part of their incoming QC and also how to implement their own end-of-line measurements to ensure correlation between the two. Specifying and testing loudspeakers can be tricky since loudspeakers are inherently nonlinear, time-variant and effected by their working conditions & environment. This paper examines the loudspeaker characteristics that can be measured, and discusses common pitfalls and how to avoid them on a loudspeaker production line. Several different audio test methods and measurements for end-of- the-line speaker quality control are evaluated, and the most relevant ones identified. Speed, statistics, and full traceability are also discussed. Keywords: end of line loudspeaker testing, frequency response, distortion, Rub & Buzz, limits INTRODUCTION In order to guarantee quality while keeping testing fast and accurate, it is important for audio manufacturers to perform only those tests which will easily identify out-of-specification products, and omit those which do not provide additional information that directly pertains to the quality of the product or its likelihood of failure. -
Standard for Terminology V2
Joint Monitoring Programme for Ambient Noise North Sea 2018 – 2020 Standard for Terminology WP 3 Deliverable/Task: 3.1 Authors: L. Wang, S Robinson Affiliations: NPL Version 2.0 Date: March 2020 INTERREG North Sea Region Jomopans Project Full Title Joint Monitoring Programme for Ambient Noise North Sea Project Acronym Jomopans Programme Interreg North Region Programme Programme Priority Priority 3 Sustainable North Sea Region Colophon Name Niels Kinneging (Project Manager) Organization Name Rijkswaterstaat Email [email protected] Phone +31 6 5321 5242 This report should be cited: JOMOPANS standard: Terminology for ambient ocean noise monitoring Cover picture: UK Crown copyright 2 INTERREG North Sea Region Jomopans Table of contents 1 General acoustic terms ......................................................................................................... 5 1.1 Definitions of basic quantities and metrics ............................................................................ 5 1.2 Levels used in underwater acoustics ...................................................................................11 2 Metrics for ambient noise monitoring in JOMOPANS ..........................................................14 2.1 Metrics for use in JOMOPANS ............................................................................................14 2.2 Other common metrics not used in JOMOPANS .................................................................14 3 Terminology used in acoustic modelling ..............................................................................15